Sample Paper

IIT JEE (Advanced) Entrance Sample Paper Mathematics Sample Paper

PART-3: MATHEMATICS
SECTION-1 : (Maximum Marks: 12)

This section contains four (04) questions.
Each question has FOUR options (A), (B), (C), and (D). Only one of these four options is the correct answer.
For each question, choose the option corresponding to the correct answer.
Answer to each question will be evaluated according to the following marking scheme:
Full Marks: “+3” If ONLY the correct option is chosen;
Zero Marks: “0” If none of the options is chosen (i.e. the question is unanswered);
Negative Marks: “−1” In all other cases.

Q1. Consider a triangle \(\Delta\) whose two sides lie on the \(x\)-axis and the line \(x+y+1=0\). If the orthocenter of \(\Delta\) is \((1,1)\), then the equation of the circle passing through the vertices of the triangle \(\Delta\) is

(A) \(x^{2}+y^{2}-3 x+y=0\)

(B) \(x^{2}+y^{2}+x+3 y=0\)

(D) \(x^{2}+y^{2}+x+y=0\)

Answer: B

Solution:

Image of orthocentre about any side of the triangle lies on its circumcircle. We can observe that \(x^{2}+y^{2}+x+3 y=0\) is satisfied by both \((-1,0)\) and \((1,-1)\). So, option “B” is the correct choice.

Q2. The area of the region \(\left\{(x, y): 0 \leq x \leq \frac{9}{4}, \quad 0 \leq y \leq 1, \quad x \geq 3 y, \quad x+y \geq 2\right\}\) is

(A) \(\frac{11}{32}\)

(B) \(\frac{35}{96}\)

(D) \(\frac{13}{32}\)

Answer: A

Solution:

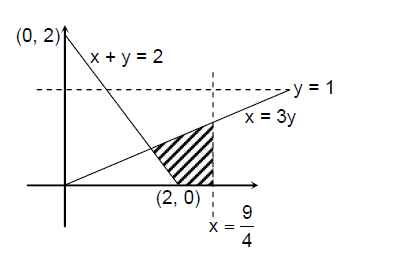
Area of the shaded region
\(
\begin{aligned}
&=\frac{1}{2}\left(\frac{2}{3}+\frac{3}{4}\right) \frac{1}{4}+\frac{1}{2} \times \frac{2}{3} \times \frac{1}{2} \\
&=\frac{11}{32}
\end{aligned}
\)

Q3. Consider three sets \(\mathrm{E}_{1}=\{1,2,3\}, \mathrm{F}_{1}=\{1,3,4\}\) and \(\mathrm{G}_{1}=\{2,3,4,5\}\). Two elements are chosen at random, without replacement, from the set \(\mathrm{E}_{1}\), and let \(\mathrm{S}_{1}\) denote the set of these chosen elements. Let \(\mathrm{E}_{2}=\mathrm{E}_{1}-\mathrm{S}_{1}\) and \(\mathrm{F}_{2}=\mathrm{F}_{1} \cup \mathrm{S}_{1}\). Now two elements are chosen at random, without replacement, from the set \(\mathrm{F}_{2}\) and let \(\mathrm{S}_{2}\) denote the set of these chosen elements.

Let \(\mathrm{G}_{2}=\mathrm{G}_{1} \cup \mathrm{S}_{2}\). Finally, two elements are chosen at random, without replacement, from the set \(\mathrm{G}_{2}\) and let \(\mathrm{S}_{3}\) denote the set of these chosen elements.

Let \(\mathrm{E}_{3}=\mathrm{E}_{2} \cup \mathrm{S}_{3}\). Given that \(\mathrm{E}_{1}=\mathrm{E}_{3}\), let \(\mathrm{p}\) be the conditional probability of the event \(\mathrm{S}_{1}=\{1,2\}\). Then the value of \(\mathrm{p}\) is

(A) \(\frac{1}{5}\)

(B) \(\frac{3}{5}\)

(D) \(\frac{2}{5}\)

Answer: A

Solution:

\(\begin{array}{llllll} & \mathrm{S}_{1} & \mathrm{~F}_{2}=\mathrm{F}_{1} \cup \mathrm{S}_{1} & \mathrm{~S}_{2} & \mathrm{G}_{1} \cup \mathrm{S}_{2}=\mathrm{G}_{2} & \mathrm{~S}_{3} \\ \text { (i) } & \{1,2\} & \{1,2,3,4) & \{1, \mathrm{x}\} & \{1,2,3,4,5\} & \{1,2\} \\ \text { (ii) } & \{2,3\} & \{1,2,3,4\} & \{1, \mathrm{x}\} & \{1,2,3,4,5\} & \{2,3\} \\ & & & \{\mathrm{x}, \mathrm{y}\} \text { (where x and y } & \text { or }\{2,3,4,5\} & \\ \text { (iii) } & \{1,3\} & \{1,3,4\} & \{1, \mathrm{x}\} \text { are other than 1) } & \{1,2,3,4,5\} & \{1,3\}\end{array}\)
(I) \(\quad \mathrm{P}_{1}=\frac{{ }^{2} c_{2}}{{ }^{3} c_{2}} \cdot \frac{{ }^{3} c_{1}}{{ }^{4} c_{2}} \cdot \frac{{ }^{2} c_{1}}{{ }^{5} c_{2}}=\frac{1}{60}\)
(ii) \(\mathrm{P}_{2}=\frac{1}{3}\left(\frac{{ }^{3} c_{1}}{{ }^{4} c_{2}} \times \frac{{ }^{2} c_{2}}{{ }^{5} c_{2}}+\frac{{ }^{3} c_{2}}{{ }^{4} c_{2}} \times \frac{{ }^{2} c_{2}}{{ }^{4} c_{2}}\right)=\frac{2}{45}\)
(iii) \(\quad \mathrm{P}_{3}=\frac{1}{{ }^{3} \mathrm{c}_{1}} \times \frac{{ }^{2} \mathrm{c}_{1}}{{ }^{3} \mathrm{c}_{2}} \times \frac{{ }^{2} \mathrm{c}_{2}}{{ }^{5} \mathrm{c}_{2}}=\frac{1}{45}\)
Conditional probability \(=\frac{P_{1}}{P_{1}+P_{2}+P_{3}}=\frac{1}{5}\)

Q4. Let \(\theta_{1}, \theta_{2}, \ldots, \theta_{10}\) be positive valued angles (in radian) such that \(\theta_{1}+\theta_{2}+\ldots+\theta_{10}=2 \pi\). Define the complex numbers \(z_{1}=e^{i \theta_{1}}, z_{k}=z_{k-1} e^{i \theta_{k}}\) for \(k=2,3, \ldots, 10\), where \(i=\sqrt{-1}\). Consider the statements P and Q given below :
\(\mathrm{P}:\left|\mathrm{z}_{2}-\mathrm{z}_{1}\right|+\left|\mathrm{z}_{3}-\mathrm{z}_{2}\right|+\ldots+\left|\mathrm{z}_{10}-\mathrm{z}_{9}\right|+\left|\mathrm{z}_{1}-\mathrm{z}_{10}\right| \leq 2 \pi\)
Q : \(\left|z_{2}^{2}-z_{1}^{2}\right|+\left|z_{3}^{2}-z_{2}^{2}\right|+\ldots .+\left|z_{10}^{2}-z_{9}^{2}\right|+\left|z_{1}^{2}-z_{10}^{2}\right| \leq 4 \pi\)
Then,

(A) P is TRUE and Q is FALSE

(B) Q is TRUE and P is FALSE

(D) both P and Q are FALSE

Answer: C

Solution:

\(
\begin{aligned}
&\because z_{1}=e^{i \theta_{1}} \\
&\text { So, } z_{2}=e^{i\left(\theta_{1}+\theta_{2}\right)} \\
&z_{3}=e^{i\left(\theta_{1}+\theta_{2}+\theta_{3}\right)} \\
&\vdots \\
&z_{10}=e^{i\left(\theta_{1}+\theta_{2}+\ldots .+\theta_{10}\right)}=e^{i(2 \pi)}
\end{aligned}
\)
Sum of all the chord length \(<\) Circumference
So, \(\sum\left|z_{2}-z_{1}\right| \leq 2 \pi\)
Also, \(2\left|z_{2}-z_{1}\right| \geq\left|z_{2}^{2}-z_{1}^{2}\right|\)
Hence, \(2\left(\left|z_{2}-z_{1}\right|+\ldots .+\left|z_{10}-z_{1}\right|\right) \leq 2(2 \pi)=4 \pi\)
So for, we have \(P \leq 2 \pi\) and \(Q \leq 4 \pi\)

Section-II: (Maximum Marks : 12)

This section contains three (03) question stems.
There are two(02) questions corresponding to each question stem.
The answer to each question is a numerical value.
For each question, enter the correct numerical value corresponding to the answer in the designated
place using the mouse and the on-screen virtual numeric keypad.
If the numerical value has more than two decimal places, truncate/round-off the value to TWO
decimal places.
Answers to each question will be evaluated according to the following marking scheme:
Full Marks: “+2” If only the correct numerical value is entered at the designated place;
Zero Marks: “0” In all other cases

Question Stem for Question Nos. 5 and 6

Three numbers are chosen at random, one after another with replacement, from the set \(S=\{1,2,3, \ldots, 100\}\). Let \(p_{1}\) be the probability that the maximum of chosen numbers is at least 81 and \(\mathrm{p}_{2}\) be the probability that the minimum of chosen numbers is at most 40.

Q5. The value of \(\frac{625 p_{1}}{4}\) is _________.

Answer: 76.25

Solution:

\(\mathrm{p}_{1}=\) probability that maximum of chosen numbers is at least 81
\(\mathrm{p}_{1}=1\) – probability that maximum of chosen number is at most 80
\(\mathrm{p}_{1}=1-\frac{80 \times 80 \times 80}{100 \times 100 \times 100}=1-\frac{64}{125}\)
\(\mathrm{p}_{1}=\frac{61}{125}\)
\(\frac{625 \mathrm{p}_{1}}{4}=\frac{625}{4} \times \frac{61}{125}=\frac{305}{4}=76.25\)

Q6. The value of \(\frac{125}{4} \mathrm{p}_{2}\) is _______.

Answer: 24.50

Solution:

\(\mathrm{p}_{2}=\) probability that minimum of chosen numbers is at most 40
\(=1-\) probability that minimum of chosen numbers is at least 41
\(
\begin{aligned}
&=1-\left(\frac{600}{100}\right)^{3} \\
&=1-\frac{27}{125}=\frac{98}{125} \\
&\therefore \frac{125}{4} \mathrm{p}_{2}=\frac{125}{4} \times \frac{98}{125}=24.50
\end{aligned}
\)

Question Stem for Question Nos. 7 and 8

Let \(\alpha, \beta\) and \(\gamma\) be real numbers such that the system of linear equations
\(
\begin{gathered}
x+2 y+3 z=\alpha \\
4 x+5 y+6 z=\beta \\
7 x+8 y+9 z=\gamma-1
\end{gathered}
\)
is consistent. Let [/latex]|\mathrm{M}|[/latex] represent the determinant of the matrix
\(
\mathbf{M}=\left[\begin{array}{ccc}
\alpha & 2 & \gamma \\
\beta & 1 & 0 \\
-1 & 0 & 1
\end{array}\right]
\)
Let \(P\) be the plane containing all those \((\alpha, \beta, \gamma)\) for which the above system of linear equations is consistent, and \(\mathrm{D}\) be the square of the distance of the point \((0,1,0)\) from the plane \(\mathrm{P}\)

Q7. The value of \(|\mathrm{M}|\) is ______.

Answer: 1

Q8. The value of D is _________.

Answer: 1.5

Solution:

\(
\begin{aligned}
&7 x+8 y+9 z-(\gamma-1)=A(4 x+5 y+6 z-\beta)+B(x+2 y+3 z-\alpha) \\
&x: 7=4 A+B \\
&y: 8=5 \mathrm{A}+2 \mathrm{~B} \\
&A=2, B=-1 \\
&\text { const. term }:-(\gamma-1)=-A \beta-\alpha B \Rightarrow-(\gamma-1) \equiv 2 \beta+\alpha \\
&\alpha-2 \beta+\gamma=1 \\
&M=\left(\begin{array}{lll}
\alpha & 2 & \gamma \\
\beta & 1 & 0 \\
-1 & 0 & 1
\end{array}\right)=\alpha-2 \beta+\gamma=1
\end{aligned}
\)
Plane \(\mathrm{P}: \mathrm{x}-2 \mathrm{y}+\mathrm{z}=1\)
Perpendicular distance \(=\left|\frac{3}{\sqrt{6}}\right|=\mathrm{P} \Rightarrow \mathrm{D}=\mathrm{P}^{2}=\frac{9}{6}=1.5\)

Question Stem for Question Nos. 9 and 10

Consider the lines \(\mathrm{L}_{1}\) and \(\mathrm{L}_{2}\) defined by \(\mathrm{L}_{1}: \mathrm{x} \sqrt{2}+\mathrm{y}-1=0\) and \(\mathrm{L}_{2}: \mathrm{x} \sqrt{2}-\mathrm{y}+1=0\)
For a fixed constant \(\lambda\), let \(\mathrm{C}\) be the locus of a point \(\mathrm{P}\) such that the product of the distance of \(\mathrm{P}\) from \(\mathrm{L}_{1}\) and the distance of \(\mathrm{P}\) from \(\mathrm{L}_{2}\) is \(\lambda^{2}\). The line \(\mathrm{y}=2 \mathrm{x}+1\) meets \(\mathrm{C}\) at two points \(\mathrm{R}\) and \(\mathrm{S}\), where the distance between \(\mathrm{R}\) and \(\mathrm{S}\) is \(\sqrt{270}\).

Let the perpendicular bisector of RS meet \(\mathrm{C}\) at two distinct points \(\mathrm{R}^{\prime}\) and \(\mathrm{S}^{\prime}\). Let \(\mathrm{D}\) be the square of the distance between \(R^{\prime}\) and \(S^{\prime}\).

Q9. The value of \(\lambda^{2}\) is ________.

Answer: 9

Solution:

\(\begin{aligned}
&\mathrm{P}(\mathrm{x}, \mathrm{y}) \quad\left|\frac{\sqrt{2} \mathrm{x}+\mathrm{y}-1}{\sqrt{3}}\right|\left|\frac{\sqrt{2} \mathrm{x}-\mathrm{y}+1}{\sqrt{3}}\right|=\lambda^{2} \\
&\left|\frac{2 \mathrm{x}^{2}-(\mathrm{y}-1)^{2}}{3}\right|=\lambda^{2}, \mathrm{C}:\left|2 \mathrm{x}^{2}-(\mathrm{y}-1)^{2}\right|=3 \lambda^{2} \\
&\text { line } \mathrm{y}=2 \mathrm{x}+1, \mathrm{RS}=\sqrt{\left(\mathrm{x}_{1}-\mathrm{x}_{2}\right)^{2}+\left(\mathrm{y}_{1}-\mathrm{y}_{2}\right)^{2}}, \mathrm{R}\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right) \text { and } \mathrm{S}\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right) \\
&\mathrm{y}_{1}=2 \mathrm{x}_{1}+1 \text { and } \mathrm{y}_{2}=2 \mathrm{x}_{2}+1 \Rightarrow\left(\mathrm{y}_{1}-\mathrm{y}_{2}\right)=2\left(\mathrm{x}_{1}-\mathrm{x}_{2}\right) \\
&\mathrm{RS}=\sqrt{5\left(\mathrm{x}_{1}-\mathrm{x}_{2}\right)^{2}}=\sqrt{5}\left|\mathrm{x}_{1}-\mathrm{x}_{2}\right| \\
&\text { solve curve } \mathrm{C} \text { and line } \mathrm{y}=2 \mathrm{x}+1 \text { we get } \\
&\left|2 \mathrm{x}^{2}-(2 \mathrm{x})^{2}\right|=3 \lambda^{2} \Rightarrow \mathrm{x}^{2}=\frac{3 \lambda^{2}}{2} \\
&\mathrm{RS}=\sqrt{5}\left|\frac{2 \sqrt{3} \lambda}{\sqrt{2}}\right|=\sqrt{30} \lambda=\sqrt{270} \Rightarrow 30 \lambda^{2}=270 \Rightarrow \lambda^{2}=9
\end{aligned}\)

Q10. The value of D is __________.

Answer: 77.14

Solution:

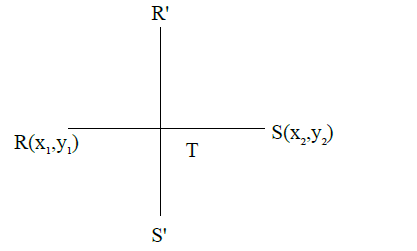
Perpendicular bisector of RS
\(
\mathrm{T} \equiv\left(\frac{\mathrm{x}_{1}+\mathrm{x}_{2}}{2}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}\right)
\)
Here \(x_{1}+x_{2}=0\)
\(
\mathrm{T}=(0,1)
\)
Equation of
\(
\mathrm{R}^{\prime} \mathrm{S}^{\prime}:(\mathrm{y}-1)=-\frac{1}{2}(\mathrm{x}-0) \Rightarrow \mathrm{x}+2 \mathrm{y}=2
\)
\(\mathrm{R}^{\prime}\left(\mathrm{a}_{1}, \mathrm{~b}_{1}\right) \mathrm{S}^{\prime}\left(\mathrm{a}_{2}, \mathrm{~b}_{2}\right)\)
\(
\mathrm{D}=\left(\mathrm{a}_{1}-\mathrm{a}_{2}\right)^{2}+\left(\mathrm{b}_{1}-\mathrm{b}_{2}\right)^{2}=5\left(\mathrm{~b}_{1}-\mathrm{b}_{2}\right)^{2}
\)
solve \(x+2 y=2\) and \(\left|2 x^{2}-(y-1)^{2}\right|=3 \lambda^{2}\)
\(
\left|8(y-1)^{2}-(y-1)^{2}\right|=3 \lambda^{2} \Rightarrow(y-1)^{2}=\left(\frac{\sqrt{3} \lambda}{\sqrt{7}}\right)^{2}
\)
\(
\mathrm{y}-1=\pm \frac{\sqrt{3} \lambda}{\sqrt{7}} \Rightarrow \mathrm{b}_{1}=1+\frac{\sqrt{3} \lambda}{\sqrt{7}}, \mathrm{~b}_{2}=1-\frac{\sqrt{3} \lambda}{\sqrt{17}}
\)
\(
\mathrm{D}=5\left(\frac{2 \sqrt{3} \lambda}{\sqrt{7}}\right)^{2}=\frac{5 \times 4 \times 3 \lambda^{2}}{7}=\frac{5 \times 4 \times 27}{7}=77.14
\)

SECTION-3 : (Maximum Marks : 24)

This section contains six (06) questions.
Each question has four options (A), (B), (C), and (D). One or more than one of these
four option(s) is (are) correct answer(s).
For each question, choose the option(s) corresponding to (all) the correct answer(s).
Answer to each question will be evaluated according to the following marking scheme:
Full Marks : “+4” If only (all) the correct option(s) is(are) chosen;
Partial Marks: “+3” If all the four options are correct but ONLY three options are chosen;
Partial Marks: “+2” If three or more options are correct but ONLY two options are chosen,
both of which are correct;
Partial Marks: “+1” If two or more options are correct but ONLY one option is chosen and it
is a correct option;
Zero Marks: “0” If unanswered;
Negative Marks: “−2” In all other cases

Q11. For any \(3 \times 3\) matrix \(\mathrm{M}\), let \(|\mathrm{M}|\) denote the determinant of \(\mathrm{M}\). Let
\(
\mathrm{E}=\left[\begin{array}{ccc}
1 & 2 & 3 \\
2 & 3 & 4 \\
8 & 13 & 18
\end{array}\right], P=\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{array}\right] \text { and } F=\left[\begin{array}{ccc}
1 & 3 & 2 \\
8 & 18 & 13 \\
2 & 4 & 3
\end{array}\right]
\)
If \(\mathrm{Q}\) is a nonsingular matrix of order \(3 \times 3\), then which of the following statements is (are) TRUE ?

(A) \(\mathrm{F}=\mathrm{PEP}\) and \(\mathrm{P}^{2}=\left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]\)

(B) \(\left|\mathrm{EQ}+\mathrm{PFQ}^{-1}\right|=|\mathrm{EQ}|+\left|\mathrm{PFQ}^{-1}\right|\)

(D) Sum of the diagonal entries of \(\mathrm{P}^{-1} \mathrm{EP}+\mathrm{F}\) is equal to the sum of diagonal entries of \(\mathrm{E}+\mathrm{P}^{-1} \mathrm{FP}\)

Answer: A,B & D

Solution:

\(\begin{aligned}
&\text { (A) }\mathrm{PEP}=\left(\begin{array}{lll}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{array}\right)\left(\begin{array}{ccc}
1 & 2 & 3 \\
2 & 3 & 4 \\
8 & 13 & 18
\end{array}\right)\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{array}\right)\\
&\left(\begin{array}{ccc}
1 & 2 & 3 \\
8 & 13 & 18 \\
2 & 3 & 4
\end{array}\right)\left(\begin{array}{lll}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{array}\right)=\left(\begin{array}{ccc}
1 & 3 & 2 \\
8 & 18 & 13 \\
2 & 4 & 3
\end{array}\right)\\
&\mathrm{P}^{2}=\left(\begin{array}{lll}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{array}\right)\left(\begin{array}{lll}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{array}\right)=\left(\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right)\\
&\text { (B) }\left|\mathrm{EQ}+\mathrm{PFQ}^{-1}\right|=|\mathrm{EQ}|+\left|\mathrm{PFQ}^{-1}\right|\\
&|\mathrm{E}|=0 \text { and }|\mathrm{F}|=0 \text { and }|\mathrm{Q}| \neq 0\\
&|\mathrm{EQ}|=|\mathrm{E}||\mathrm{Q}|=0,\left|\mathrm{PFQ}^{-1}\right|=\frac{|\mathrm{P}||\mathrm{F}|}{|\mathrm{Q}|}=0\\
&\mathrm{T}=\mathrm{EQ}+\mathrm{PFQ}^{-1}\\
&\mathrm{TQ}=\mathrm{EQ}^{2}+\mathrm{PF}=\mathrm{EQ}^{2}+\mathrm{P}^{2} \mathrm{EP}=\mathrm{EQ}^{2}+\mathrm{EP}=\mathrm{E}\left(\mathrm{Q}^{2}+\mathrm{P}\right)\\
&\left.|\mathrm{TQ}|=\left|\mathrm{E}\left(\mathrm{Q}^{2}+\mathrm{P}\right)\right| \Rightarrow|\mathrm{T}||\mathrm{Q}|=|\mathrm{E}|\left|\mathrm{Q}^{2}+\mathrm{P}\right|=0 \Rightarrow|\mathrm{T}|=0 \quad \text { (as }|\mathrm{Q}| \neq 0\right)\\
&\text { (C) }\left|(\mathrm{EF})^{3}\right|>|\mathrm{EF}|^{2}\\
&\text { Here } 0>0 \text { (false) }\\
&\text { (D) as } \mathrm{P}^{2}=\mathrm{I} \Rightarrow \mathrm{P}^{-1}=\mathrm{P} \text { so } \mathrm{P}^{-1} \mathrm{FP}=\mathrm{PFP}=\mathrm{PPEPP}=\mathrm{E}\\
&\text { so } \mathrm{E}+\mathrm{P}^{-1} \mathrm{FP}=\mathrm{E}+\mathrm{E}=2 \mathrm{E}\\
&\mathrm{P}^{-1} \mathrm{EP}+\mathrm{F} \Rightarrow \mathrm{PEP}+\mathrm{F}=2 \mathrm{PEP}
\end{aligned}\)

Therefore, (C) is False.

Q12. Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be defined by
\(
f(x)=\frac{x^{2}-3 x-6}{x^{2}+2 x+4}
\)
Then which of the following statements is (are) TRUE?

(A) \(f\) is decreasing in the interval \((-2,-1)\)

(B) \(f\) is increasing in the interval \((1,2)\)

(D) Range of \(f\) is \(\left[-\frac{3}{2}, 2\right]\)

Answer: A & B

Solution:

\(\begin{aligned}
&f^{\prime}(x)=\frac{5 x(x+4)}{\left(x^{2}+2 x+4\right)^{2}} \\
&f(0)=-\frac{3}{2} \text { (point of local minima) } \\
&f(-4)=\frac{11}{6} \text { (point of local maxima) }
\end{aligned}\)

Q13. Let \(\mathrm{E}, \mathrm{F}\) and \(\mathrm{G}\) be three events having probabilities \(\mathrm{P}(\mathrm{E})=\frac{1}{8}, \mathrm{P}(\mathrm{F})=\frac{1}{6}\) and \(\mathrm{P}(\mathrm{G})=\frac{1}{4}\), and let \(\mathrm{P}(\mathrm{E} \cap \mathrm{F} \cap \mathrm{G})=\frac{1}{10}\)
For any event \(\mathrm{H}\), if \(\mathrm{H}^{\mathrm{C}}\) denotes its complement, then which of the following statements is(are) TRUE ?

(A) \(\mathrm{P}\left(\mathrm{E} \cap \mathrm{F} \cap \mathrm{G}^{\mathrm{C}}\right) \leq \frac{1}{40}\)

(B) \(\mathrm{P}\left(\mathrm{E}^{\mathrm{C}} \cap \mathrm{F} \cap \mathrm{G}\right) \leq \frac{1}{15}\)

(D) \(\mathrm{P}\left(\mathrm{E}^{\mathrm{C}} \cap \mathrm{F}^{\mathrm{C}} \cap \mathrm{G}^{\mathrm{C}}\right) \leq \frac{5}{12}\)

Answer: A, B & C

Q14. For any \(3 \times 3\) matrix \(M\), let \(|\mathrm{M}|\) denote the determinant of \(\mathrm{M}\). Let \(\mathrm{I}\) be the \(3 \times 3\) identity matrix. Let \(E\) and \(F\) be two \(3 \times 3\) matrices such that (I – EF) is invertible. If \(G=(I-E F)^{-1}\), then which of the following statements is (are) TRUE?

(A) \(|\mathrm{FE}|=|\mathrm{I}-\mathrm{EF}||\mathrm{FGE}|\)

(B) \(|\mathrm{I}-\mathrm{FE}|(\mathrm{I}+\mathrm{FGE})=\mathrm{I}\)

(D) \((\mathrm{I}-\mathrm{FE})(\mathrm{I}-\mathrm{FGE})=\mathrm{I}\)

Answer: A, B, and C

Solution:

\(
\mathrm{G}(\mathrm{I}-\mathrm{EF})=(\mathrm{I}-\mathrm{EF}) \mathrm{G}=\mathrm{I}
\)
\(
\Rightarrow \mathrm{G}-\mathrm{GEF}=\mathrm{G}-\mathrm{EFG}=\mathrm{I}
\)

(A) \(|\mathrm{FE}|=|\mathrm{I}-\mathrm{FE}||\mathrm{FGE}|=|\mathrm{FGE}-\mathrm{FE} \mathrm{FGE}|
=|\mathrm{FGE}-\mathrm{F}(\mathrm{G}-\mathrm{I}) \mathrm{E}|=|\mathrm{FGE}-\mathrm{FGE}+\mathrm{FE}|=|\mathrm{FE}|
\)

(B) \((\mathrm{I}-\mathrm{FE})(\mathrm{I}+\mathrm{FGE})=\mathrm{I}+\mathrm{FGE}-\mathrm{FE}-\mathrm{FEFGH}
=\mathrm{I}+\mathrm{FGE}-\mathrm{FE}-\mathrm{F}(\mathrm{G}-\mathrm{I}) \mathrm{E}=\mathrm{I}+\mathrm{FGE}-\mathrm{FE}-\mathrm{FGE}+\mathrm{FE}=\mathrm{I}\)

(C)

\(\begin{aligned}
&|\mathrm{I}-\mathrm{EF}| \neq 0 ; \mathrm{G}=(\mathrm{I}-\mathrm{EF})^{-1} \Rightarrow \mathrm{G}^{-1}=\mathrm{I}-\mathrm{EF} \\
&\Rightarrow \mathrm{G}(\mathrm{I}-\mathrm{EF})=\mathrm{I}=\mathrm{G}^{-1} \mathrm{G}=(\mathrm{I}-\mathrm{EF}) \mathrm{G} \\
&\Rightarrow \mathrm{G}-\mathrm{GEF}=\mathrm{I}=\mathrm{G}-\mathrm{EFG} \\
&\Rightarrow \mathrm{GEF}=\mathrm{EFG} \quad \\
\end{aligned}
\)

(D)
\(\begin{aligned}
&(\mathrm{I}-\mathrm{FE})(\mathrm{I}-\mathrm{FGE})=\mathrm{I}-\mathrm{FGE}-\mathrm{FE}+\mathrm{FEFGE} \\
=& \mathrm{I}-\mathrm{FGE}-\mathrm{FE}+\mathrm{F}(\mathrm{G}-\mathrm{I}) \mathrm{E}=\mathrm{I}-\mathrm{FGE}-\mathrm{FE}+\mathrm{FGE}-\mathrm{FE} =\mathrm{I}-2 \mathrm{FE}
\end{aligned}\)

Only D is FALSE.

Q15. For any positive integer \(n\), let \(S_{n}:(0, \infty) \rightarrow \mathbb{R}\) be defined by
\( S_{n}(x)=\sum_{k=1}^{n} \cot ^{-1}\left(\frac{1+k(k+1) x^{2}}{x}\right),\)
where for any \(x \in \mathbb{R} \cot ^{-1} x \in(0, \pi)\) and \(\tan ^{-1}(x) \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\). Then which of the following statements is (are) TRUE?

(A) \(S_{10}(x)=\frac{\pi}{2}-\tan ^{-1}\left(\frac{1+11 x^{2}}{10 x}\right)\), for all \(x>0\)

(B) \(\lim _{n \rightarrow \infty} \cot \left(S_{n}(x)\right)=x\), for all \(x>0\)

(D) \(\tan \left(S_{n}(x)\right) \leq \frac{1}{2}\), for all \(n \geq 1\) and \(x>0\)

Answer: A & B

Solution:

(A)

\(
\begin{aligned}
&S_{n}=\sum_{k=1}^{n} \cot ^{-1}\left\{\frac{1+k(k+1) x^{2}}{x}\right\} ; \sum_{k=1}^{n} \cot ^{-1}\left\{\frac{k(k+1) x^{2}+1}{(k+1) x-k x}\right\} \\
&S_{n}=\sum_{k=1}^{n} \cot ^{-1}(k x)-\cot ^{-1}(k+1) x \\
&t_{1}=\cot ^{-1}(x)-\cot ^{-1}(2 x) \\
&t_{2}=\cot ^{-1}(2 x)-\cot ^{-1}(3 x) \\
&t_{3}=\cot ^{-1}(3 x)-\cot ^{-1}(4 x) \\
&\vdots \\
&t_{n}=\cot ^{-1}(n x)-\cot ^{-1}((n+1) x) \\
&S_{n}=\cot ^{-1}(x)-\cot ^{-1}((n+1) x) \\
&\Rightarrow S_{n}=\cot ^{-1}\left(\frac{(n+1) x^{2}+1}{n x}\right) \\
&S_{10}=\cot ^{-1}\left(\frac{11 x^{2}+1}{10 x}\right)=\frac{\pi}{2}-\tan ^{-1}\left(\frac{11 x^{2}+1}{10 x}\right)
\end{aligned}
\)

(B) \(\lim _{n \rightarrow \infty} \cot \left(S_{n}(x)\right)=\lim _{n \rightarrow \infty} \cot \left(\cot ^{-1}\left(\frac{(n+1) x^{2}+1}{n x}\right)\right)=\lim _{n \rightarrow \infty} \frac{n x^{2}+x^{2}+1}{n x}=x\)

(C) \(S_{3}(x)=\cot ^{-1}\left(\frac{4 x^{2}+1}{3 x}\right)=\frac{\pi}{4} \Rightarrow \frac{1+4 x^{2}}{3 x}=1\) \(\Rightarrow 4 \mathrm{x}^{2}-3 \mathrm{x}+1=0\) have imaginary roots, C is false.

(D) \(\tan \left(S_{n}(x)\right)=\tan \left(\cot ^{-1}\left(\frac{1+(n+1) x^{2}}{n x}\right)\right)=\frac{n x}{1+(n+1) x^{2}}=\frac{1}{\frac{1}{n x}+\frac{(n+1) x}{n}}\), D is also False.

Q16. For any complex number \(\mathrm{w}=\mathrm{c}+\) id, let \(\arg (\mathrm{w}) \in(-\pi, \pi]\), where \(\mathrm{i}=\sqrt{-1}\). Let \(\alpha\) and \(\beta\) be real numbers such that for all complex numbers \(z=x+\) iy satisfying \(\arg \left(\frac{z+\alpha}{z+\beta}\right)=\frac{\pi}{4}\), the ordered pair \((\mathrm{x}, \mathrm{y})\) lies on the circle
\(x^{2}+y^{2}+5 x-3 y+4=0\)
Then which of the following statements is (are) TRUE?

(A) \(\alpha=-1\)

(B) \(\alpha \beta=4\)

(D) \(\beta=4\)

Answer: B & D

Solution:

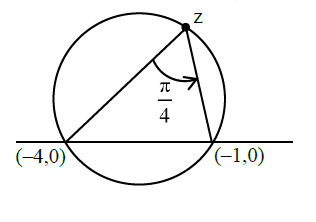
\(\arg \left(\frac{z+\alpha}{z+\beta}\right)=\frac{\pi}{4}\) implies \(z\) is on arc and \((-\alpha, 0) \&(-\beta, 0)\) subtend \(\frac{\pi}{4}\) on \(z\).
And \(z\) lies on \(x^{2}+y^{2}+5 x-3 y+4=0\); So put \(y=0\);
\(
x^{2}+5 x+4=0 \Rightarrow x=-1 ; x=-4
\); Now, \(\arg \left(\frac{\mathrm{z}+\alpha}{\mathrm{z}+\beta}\right)=\frac{\pi}{4} \Rightarrow \mathrm{z}+\alpha=(\mathrm{z}+\beta) \cdot \mathrm{r} \cdot \mathrm{e}^{i \frac{\pi}{4}}\); So, \(\mathrm{z}+\beta=\mathrm{z}+4 \Rightarrow \beta=4 \& \mathrm{z}+\alpha=\mathrm{z}+1 \Rightarrow \alpha=1\)

SECTION-4 : (Maximum Marks: 12)

This section contains three (03) questions.
The answer to each question is a non-negative integer.
For each question, enter the correct integer corresponding to the answer using the mouse and the on-screen virtual numeric keypad in the place designed to enter the answer.
Answers to each question will be evaluated according to the following marking scheme:

Full Mark: “+4” If ONLY the correct integer is entered;
Zero Marks: “0” In all other cases.

Q17.\(\text { For } x \in \mathbb{R} \text {, then number of real roots of the equation } 3x^{2}-4\left|x^{2}-1\right|+x-1=0 \text { is }\)_______.

Answer: 4

Solution:

\(
\begin{aligned}
&3 \mathrm{x}^{2}-4\left|\mathrm{x}^{2}-1\right|+\mathrm{x}-1=0 \\
&\text { Case-I: }|\mathrm{x}| \geq 1 \\
&3 \mathrm{x}^{2}-4 \mathrm{x}^{2}+4+\mathrm{x}-1=0 \\
&-\mathrm{x}^{2}+\mathrm{x}+3=0 \\
&\mathrm{x}^{2}-\mathrm{x}-3=0 \\
&\mathrm{x}=\frac{1 \pm \sqrt{1+12}}{2}=\frac{1 \pm \sqrt{13}}{2}=\frac{1+\sqrt{13}}{2}, \frac{1-\sqrt{13}}{2} \\
&|\mathrm{x}|<1 \\
&3 \mathrm{x}^{2}+4 \mathrm{x}^{2}-4+\mathrm{x}-1=0 \\
&7 \mathrm{x}^{2}+\mathrm{x}-5=0 \\
&\mathrm{x}=\frac{-1 \pm \sqrt{1+20 \times 7}}{14}=\frac{-1 \pm \sqrt{141}}{14}
\end{aligned}
\)
So, number of real roots =4

Q18. In a triangle \(\mathrm{ABC}\), let \(\mathrm{AB}=\sqrt{23}, \mathrm{BC}=3\) and \(\mathrm{CA}=4\). Then the value of \(\frac{\cot \mathrm{A}+\cot \mathrm{C}}{\cot \mathrm{B}}\) is _________.

Answer: 2

Solution:

\(\begin{aligned}
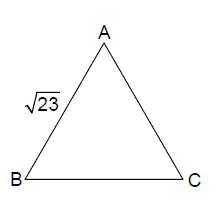
&A B=\sqrt{23}=C\\
&\mathrm{BC}=3=\mathrm{a}\\
&\mathrm{CA}=4=\mathrm{b}\\
&\frac{\cot A+\cot C}{\cot B} ; \frac{\frac{\cos A}{\sin A}+\frac{\cos C}{\sin C}}{\frac{\cos B}{\sin B}}\\
&=\frac{\cos A \sin C+\cos C \sin A}{\sin A \cdot \sin C \cdot \frac{\cos B}{\sin B}}=\frac{\sin (A+C) \cdot \sin B}{\sin A \cdot \sin C \cdot \cos B}=\frac{\sin B \cdot \sin B}{\sin A \cdot \sin C \cdot \cos B}\\
&=\frac{b^{2}}{a c \cdot \frac{\left(a^{2}+c^{2}-b^{2}\right)}{2 a c}}=\frac{2 b^{2}}{a^{2}+c^{2}-b^{2}}=\frac{2 \times 16}{9+23-16}=\frac{2 \times 16}{32-16}=\frac{2 \times 16}{16}=2
\end{aligned}\)

Q19. Let \(\overrightarrow{\mathrm{u}}, \overrightarrow{\mathrm{v}}\) and \(\overrightarrow{\mathrm{w}}\) be vectors in three-dimensional space, where \(\overrightarrow{\mathrm{u}}\) and \(\overrightarrow{\mathrm{v}}\) are unit vectors which are not perpendicular to each other and \(\vec{u} \cdot \vec{w}=1, \vec{v} \cdot \vec{w}=1, \vec{w} \cdot \vec{w}=4\)
If the volume of the parallelopiped, whose adjacent sides are represented by the vectors \(\overrightarrow{\mathrm{u}}, \overrightarrow{\mathrm{v}}\) and \(\overrightarrow{\mathrm{w}}\) , is \(\sqrt{2}\), then the value of \(|3 \vec{u}+5 \vec{v}|\) is ______.

Answer: 7

Solution:

Given, \(|\overrightarrow{\mathrm{u}}|=1 ;|\overrightarrow{\mathrm{v}}|=1 ; \overrightarrow{\mathrm{u}} \cdot \overrightarrow{\mathrm{v}} \neq 0 ; \overrightarrow{\mathrm{u}} \cdot \overrightarrow{\mathrm{w}}=1 ; \overrightarrow{\mathrm{v}} \cdot \overrightarrow{\mathrm{w}}=1\);
\(\overrightarrow{\mathrm{w}} \cdot \overrightarrow{\mathrm{w}}=|\overrightarrow{\mathrm{w}}|^{2}=4 \Rightarrow|\overrightarrow{\mathrm{w}}|=2 ;\left[\begin{array}{lll}\overrightarrow{\mathrm{u}} & \overrightarrow{\mathrm{v}} & \overrightarrow{\mathrm{w}}\end{array}\right]=\sqrt{2}\) and \(\left[\begin{array}{lll}\overrightarrow{\mathrm{u}} & \overrightarrow{\mathrm{v}} & \overrightarrow{\mathrm{w}}\end{array}\right]^{2}=\left|\begin{array}{lll}\vec{u} \cdot \overrightarrow{\mathrm{u}} & \overrightarrow{\mathrm{u}} \cdot \overrightarrow{\mathrm{v}} & \overrightarrow{\mathrm{u}} \cdot \overrightarrow{\mathrm{w}} \\ \overrightarrow{\mathrm{v}} \cdot \overrightarrow{\mathrm{u}} & \overrightarrow{\mathrm{v}} \cdot \overrightarrow{\mathrm{v}} & \overrightarrow{\mathrm{v}} \cdot \overrightarrow{\mathrm{w}} \\ \overrightarrow{\mathrm{w}} \cdot \overrightarrow{\mathrm{u}} & \overrightarrow{\mathrm{w}} \cdot \overrightarrow{\mathrm{v}} & \overrightarrow{\mathrm{w}} \cdot \overrightarrow{\mathrm{w}}\end{array}\right|=2\)
\(
\begin{aligned}
&\Rightarrow\left|\begin{array}{ccc}
1 & \overrightarrow{\mathrm{u}} . \overrightarrow{\mathrm{v}} & 1 \\
\overrightarrow{\mathrm{u}} . \overrightarrow{\mathrm{v}} & 1 & 1 \\
1 & 1 & 4
\end{array}\right|=2 \\
&\Rightarrow \overrightarrow{\mathrm{u}} \cdot \overrightarrow{\mathrm{v}}=\frac{1}{2}
\end{aligned}
\)
So, \(|3 \overrightarrow{\mathrm{u}}+5 \overrightarrow{\mathrm{v}}|=\sqrt{9|\overrightarrow{\mathrm{u}}|^{2}+25|\overrightarrow{\mathrm{v}}|^{2}+2 \cdot 3 \cdot 5 \overrightarrow{\mathrm{u}} \cdot \overrightarrow{\mathrm{v}}}\) \(=\sqrt{9+25+30\left(\frac{1}{2}\right)}=\sqrt{49}=7\)

Previous Lesson

Back to Lesson