Sample Paper

IIT JEE (Advanced) Entrance Sample Paper Physics Sample Paper

PART-1: PHYSICS
SECTION-1 : (Maximum Marks: 12)

This section contains four (04) questions.
Each question has four options (A), (B), (C), and (D). Only one of these options is the correct answer.
For each question, choose the option corresponding to the correct answer.
Answers to each question will be evaluated according to the following marking scheme:

Full Marks: “+3″ If only the correct option is chosen;
Zero Marks: “0″ If none of the options is chosen (i.e. the question is unanswered);
Negative Marks: “−1″ In all other cases.

Q1. The smallest division on the main scale of a Vernier calipers is 0.1 cm. Ten divisions of the Vernier scale correspond to nine divisions of the main scale. The figure below on the left shows the reading of this calipers with no gap between its two jaws. The figure on the right shows the reading with a solid sphere held between the jaws. The correct diameter of the sphere is

(A) 3.07 cm

(B) 3.11 cm

(D) 3.17 cm

Answer: C

Solution:

$\begin{aligned}
&\text { Given } 10 \mathrm{VSD}=9 \mathrm{MSD}; \quad \text { Here MSD } \rightarrow \text { Main Scale division }\\
&1 \mathrm{VSD}=\frac{9}{10} \mathrm{MSD}; \quad \mathrm{VSD} \rightarrow \text { Vernier Scale division }\\
&\text { Least count }=1 \mathrm{MSD}-1 \mathrm{VSD}\\
&=\left(1-\frac{9}{10}\right) \mathrm{MSD}\\
&=0.1 \mathrm{MSD}\\
&=0.1 \times 0.1 \mathrm{~cm}\\
&=0.01 \mathrm{~cm}\\
&\text { As ‘ } 0 \text { ‘ of V.S. lie before ‘0’ of M.S. }\\
&\text { Zero error }=-[10-6] \text { Least Count }\\
&=-4 \times 0.01 \mathrm{~cm}\\
&=-0.04 \mathrm{~cm}\\
&\text { Reading }=3.1 \mathrm{~cm}+1 \times \mathrm{LC}\\
&=3.4 \mathrm{~cm}+1 \times 0.01 \mathrm{~cm}\\
&=3.11 \mathrm{~cm}\\
&\text { True diameter }=\text { Reading }-\text { Zero error }\\
&=3.11-(-0.04) \mathrm{cm}=3.15 \mathrm{~cm}
\end{aligned}$\\

Q2. An ideal gas undergoes a four-step cycle as shown in the P – V diagram below. During this cycle, heat is absorbed by the gas in

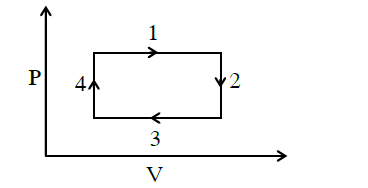
(A) steps 1 and 2

(B) steps 1 and 3

(D) steps 2 and 4

Answer: C

Q3. An extended object is placed at point $\mathrm{O}, 10 \mathrm{~cm}$ in front of a convex lens $\mathrm{L}_{1}$ and a concave lens $\mathrm{L}_{2}$ is placed $10 \mathrm{~cm}$ behind it, as shown in the figure. The radii of curvature of all the curved surfaces in both the lenses are $20 \mathrm{~cm}$. The refractive index of both the lenses is $1.5$. The total magnification of this lens system is

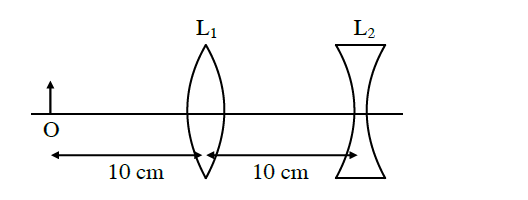
(A) 0.4

(B) 0.8

(D) 1.6

Answer: B

Q4. A heavy nucleus Q of half-life 20 minutes undergoes alpha decay with probability of 60% and beta decay with probability of 40%. Initially, the number of Q nuclei is 1000. The number of alpha decay of Q in the first one hour is

(A) 50

(B) 75

(D) 525

Answer: D

Solution:

Out of 1000 nuclei of $Q 60 \%$ may go $\alpha$-decay
$\Rightarrow \quad 600$ nuclei may have $\alpha$-decay
$
\lambda=\frac{\ln 2}{t_{1 / 2}}=\frac{\ln 2}{20}
$
$t=1$ hour $=60$ minutes
Using
$
\begin{aligned}
\mathrm{N} &=\mathrm{N}_{0} \mathrm{e}^{-\lambda \mathrm{t}} \\
&=600 \times \mathrm{e}^{-\frac{\ln 2}{20} \times 60} \\
\mathrm{~N} &=75
\end{aligned}
$
$\Rightarrow \quad 75$ Nuclei are left after one hour
So, No. of nuclei decayed
$
=600-75=525
$

SECTION-2 : (Maximum Marks: 12)

This section contains three (03) question stems.
There are two(02) questions corresponding to each question stem.
The answer to each question is a numerical value.
For each question, enter the correct numerical value corresponding to the answer in the designated place using the mouse and the on-screen virtual numeric keypad.
If the numerical value has more than two decimal places, truncate/round off the value to two decimal places.
Answers to each question will be evaluated according to the following marking scheme:
Full Marks: “+2” If only the correct numerical value is entered at the designated place;
Zero Marks: “0” In all other cases

Question Stem for Question Numbers 5 and 6

A projectile is thrown from a point $\mathrm{O}$ on the ground at an angle $45^{\circ}$ from the vertical and with a speed $5 \sqrt{2} \mathrm{~m} / \mathrm{s}$. The projectile at the highest point of its trajectory splits into two equal parts. One part falls vertically down to the ground, $0.5 \mathrm{~s}$ after the splitting. The other part, $\mathrm{t}$ seconds after the splitting, falls to the ground at a distance $\mathrm{x}$ meters from the point $\mathrm{O}$. The acceleration due to gravity $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}$.

Q5. The value of t is ___.

Answer: 0.5

Solution:

After splitting $1^{\text {st }}$ mass takes $0.5 \mathrm{sec}$ to reach ground. Initial velocity is same for both mass at the highest point in the vertical direction. Displacement and acceleration in the vertical direction is also same. So, $2^{\text {nd }}$ mass will also take $0.5$ sec to reach ground.

Q6. The value of x is ___.

Answer: 7.50

Solution:

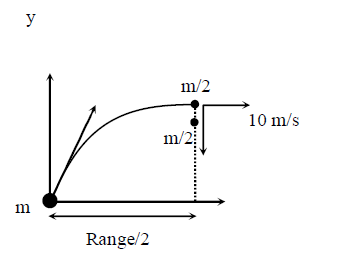
Velocity of projectile at highest point $5 \mathrm{~m} / \mathrm{s} \hat{\mathrm{i}}$
Since, there is no external force in horizontal direction so by conservation of momentum
$
\mathrm{m}(5)=\frac{\mathrm{m}}{2}(0)+\frac{\mathrm{m}}{2}(\mathrm{v})
$
$
\overrightarrow{\mathrm{V}}=10 \mathrm{~m} / \mathrm{s} \hat{\mathrm{i}}
$
Distance covered by second mass before landing $=$ $\frac{\text { Range }}{2}+10(\mathrm{t})=7.5 \mathrm{~m}$

Question Stem for Question Numbers 7 and 8

In the circuit shown below, the switch $\mathrm{S}$ is connected to position $\mathrm{P}$ for a long time so that the charge on the capacitor becomes $\mathrm{q}_{1} \mu \mathrm{C}$. Then $\mathrm{S}$ is switched to position $\mathrm{Q}$. After a long time, the charge on the capacitor is $\mathrm{q}_{2} \mu \mathrm{C}$.

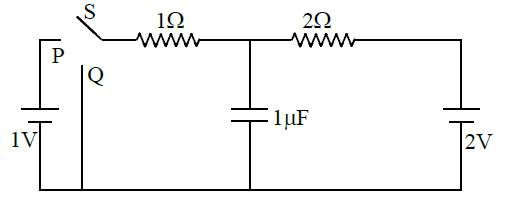
Q7. The magnitude of q1 is ___.

Answer: 1.33

Solution:

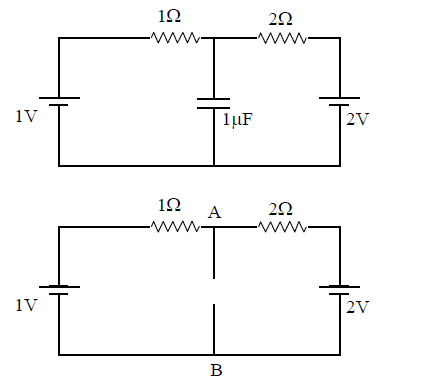
After a long time, the capacitor is fully charged and no current flows through the capacitor which is equivalent to an open circuit. We can replace the capacitor with an open circuit as shown in the above figure.
$I$ current in circuit $=1 / 3$ ampere $\mathrm{v}_{\mathrm{AB}}=2-2\left(\frac{1}{3}\right)=\frac{4}{3}$ volt
So, $\mathrm{q}_{1}=\mathrm{CV}=\frac{4}{3} \mu \mathrm{C}$

Q8. The magnitude of q2 is ___.

Answer: 0.67

Solution:

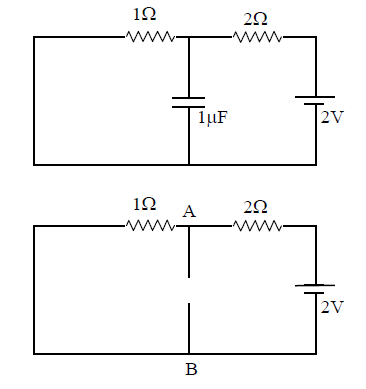
After long time $I$ circuit $=\frac{2}{3}$ ampere
$
\mathrm{v}_{\mathrm{AB}}=2-2\left(\frac{2}{3}\right)=\frac{2}{3} \text { volt }
$
So, $\mathrm{q}_{2}=\mathrm{CV}=(1)\left(\frac{2}{3}\right)=\frac{2}{3} \mu \mathrm{C}$

Question Stem for Question Nos. 9 and 10

Two-point charges $-Q$ and $+Q / \sqrt{3}$ are placed in the xy-plane at the origin $(0,0)$ and a point $(2,0)$, respectively, as shown in the figure. This results in an equipotential circle of radius $R$ and potential $\mathrm{V}=0$ in the xy-plane with its center at $(b, 0)$. All lengths are measured in meters.

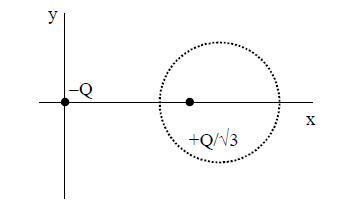
Q9. The value of R is ___ meter.

Answer: 1.73

Solution:

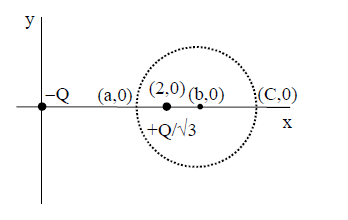
Lets take two points $(\mathrm{a}, 0)$ and $(\mathrm{C}, 0)$ on equipotential circle.
Net potential at $(\mathrm{C}, 0)=0$
$
\begin{aligned}
&\frac{K(-q)}{C}+\frac{K q}{\frac{\sqrt{3}}{(C-2)}}=0 \\
&\frac{1}{C}=\frac{1}{\sqrt{3}(C-2)} \\
&\Rightarrow \sqrt{3} C-2 \sqrt{3}=C \\
&\Rightarrow(\sqrt{3}-1) \mathrm{C}=2 \sqrt{3} \\
&\Rightarrow \mathrm{C}=\frac{2 \sqrt{3}}{\sqrt{3}-1} \\
&\text { Potential net at }(\mathrm{a}, 0)=0 \\
&\frac{\mathrm{K}(-\mathrm{q})}{\mathrm{a}}+\frac{\mathrm{K} \frac{\mathrm{q}}{\sqrt{3}}}{(2-\mathrm{a})}=0 \\
&\Rightarrow \frac{1}{\mathrm{a}}=\frac{1}{\sqrt{3}(2-\mathrm{a})} \\
&\Rightarrow 2 \sqrt{3}-\sqrt{3} \mathrm{a}=\mathrm{a} \\
&\Rightarrow \mathrm{a}=\frac{2 \sqrt{3}}{1+\sqrt{3}} \\
&\text { So, Radius }=\frac{\mathrm{C}-\mathrm{a}}{2}=\frac{\sqrt{3}-1}{\sqrt{3}}-\frac{2 \sqrt{3}}{\sqrt{3}+1} \\
&=\sqrt{3}\left(\frac{1}{\sqrt{3}-1}-\frac{1}{\sqrt{3}+1}\right)=\sqrt{3}\left(\frac{\sqrt{3}+1-\sqrt{3}+1}{3-1}\right) \\
&\text { Radius }=\sqrt{3}
\end{aligned}$

Q10. The value of b is ___ meter.

Answer: 3

Solution:

$\begin{aligned}
&\mathrm{b}=\mathrm{a}+\text { radius } \\
&=\frac{2 \sqrt{3}}{\sqrt{3}+1}+\sqrt{3}=\frac{2 \sqrt{3}+3+\sqrt{3}}{1+\sqrt{3}} \\
&=\frac{3 \sqrt{3}+3}{1+\sqrt{3}}=3 \\
&\text { Center }=(3,0)
\end{aligned}$

SECTION-3 : (Maximum Marks : 24)

This section contains SIX (06) questions.
Each question has four options (A), (B), (C), and (D). One or more than one of these four option(s) is (are) correct answer(s).
For each question, choose the option(s) corresponding to (all) the correct answer(s).
Answers to each question will be evaluated according to the following marking scheme:
Full Marks: “+4” If only (all) the correct option(s) is(are) chosen;
Partial Marks: “+3” If all the four options are correct but ONLY three options are chosen;
Partial Marks: “+2” If three or more options are correct but ONLY two options are chosen, both of which are correct;
Partial Marks: “+1” If two or more options are correct but ONLY one option is chosen and it is a correct option;
Zero Marks: “0” If unanswered;
Negative Marks: “−2” In all other cases.
For example, in a question, if (A), (B), and (D) are the only three options corresponding to correct answers, then
choosing only (A), (B), and (D) will get +4 marks;
choosing only (A) and (B) will get +2 marks;
choosing only (A) and (D) will get +2 marks;
choosing only (B) and (D) will get +2 marks;
choosing only (A) will get +1 mark;
choosing only (B) will get +1 mark;
choosing only (D) will get +1 mark;
choosing no option(s) (i.e. the question is unanswered) will get 0 marks and choosing any other option(s) will get −2 marks

Q11. A horizontal force $F$ is applied at the center of mass of a cylindrical object of mass $\mathrm{m}$ and radius $R$, perpendicular to its axis as shown in the figure. The coefficient of friction between the object and the ground is $\mu$. The center of mass of the object has an acceleration $a$. The acceleration due to gravity is $g$. Given that the object rolls without slipping, which of the following statement(s) is(are) correct?

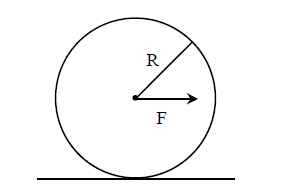
(A) For the same $F$, the value of $a$ does not depend on whether the cylinder is solid or hollow

(B) For a solid cylinder, the maximum possible value of $a$ is $2 \mu \mathrm{g}$

(D) For a thin-walled hollow cylinder, $a=\frac{F}{2 m}$

Answer: B, D

Solution:

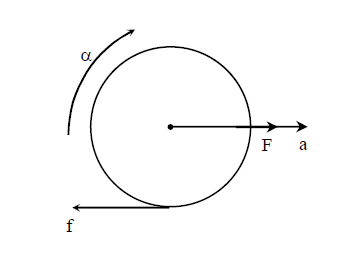
$\begin{array}{ll}F-f=m a & \\ f R=I \alpha & \text { (about center of mass) } \\ a=R \alpha & \text { (pure rolling) }\end{array}$
For hollow cylinder $a=\frac{F}{2 m}, f=\frac{F}{2}$
For solid cylinder, $a=\frac{2 F}{3 m}, f=\frac{F}{3}$
Also for solid cylinder $\frac{F}{2} \leq \mu m g$
Therefore $\mathrm{a} \leq 2 \mu \mathrm{g}$

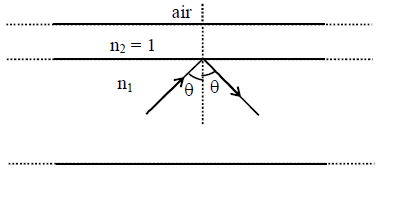
Q12. A wide slab consisting of two media of refractive indices $\mathrm{n}_{1}$ and $\mathrm{n}_{2}$ is placed in air as shown in the figure. A ray of light is incident from medium $n_{1}$ to $n_{2}$ at an angle $\theta$, where $\sin \theta$ is slightly larger than $1 / n_{1}$. Take refractive index of air as 1 . Which of the following statement(s) is(are) correct?

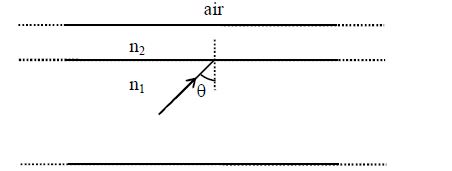
(A) The light ray enters air if $\mathrm{n}_{2}=\mathrm{n}_{1}$

(B) The light ray is finally reflected back into the medium of refractive index $\mathrm{n}_{1}$ if $\mathrm{n}_{2}<\mathrm{n}_{1}$

(C) The light ray is finally reflected back into the medium of refractive index $\mathrm{n}_{1}$ if $\mathrm{n}_{2}>\mathrm{n}_{1}$

(D) The light ray is reflected back into the medium of refractive index $\mathrm{n}_{1}$ if $\mathrm{n}_{2}=1$

Answer: B, C & D

Solution: The ray diagram for the following conditions are

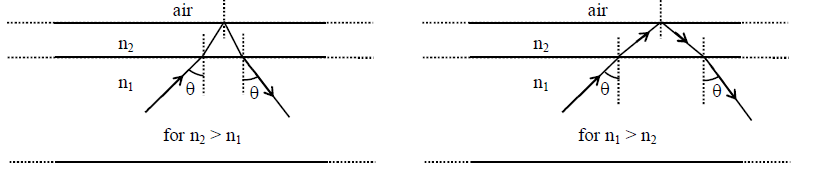
The light finally must reflected back in medium of refractive index $\mathrm{n}_{1}$ for all values of $\mathrm{n}_{2}$.

Q13. A particle of mass $M=0.2 \mathrm{~kg}$ is initially at rest in the $x y$-plane at a point $(\mathrm{x}=-l, \mathrm{y}=-h)$, where $l=10 \mathrm{~m}$ and $h=1 \mathrm{~m}$. The particle is accelerated at time $\mathrm{t}=0$ with a constant acceleration $\mathrm{a}=10 \mathrm{~m} / \mathrm{s}^{2}$ along the positive $\mathrm{x}$-direction. Its angular momentum and torque with respect to the origin, in SI units, are represented by $\vec{L}$ and $\vec{\tau}$, respectively. $\hat{i}, \hat{j}$ and $\hat{k}$ are unit vectors along the positive $x, y$ and z-directions, respectively. If $\hat{k}=\hat{i} \times \hat{j}$ then which of the following statement(s) is (are) correct ?

(A) The particle arrives at the point $(x=l, y=-h)$ at time $\mathrm{t}=2 \mathrm{~s}$.

(B) $\vec{\tau}=2 \hat{\mathrm{k}}$ when the particle passes through the point $(x=l, y=-h)$

(D) $\vec{\tau}=\hat{\mathrm{k}}$ when the particle passes through the point $(x=0, y=-h)$

Answer: A, B & C

Solution:

$\begin{aligned}
&\text { Time taken to reach from }(-\ell,-\mathrm{h}) \text { to }(\ell,-\mathrm{h}) \text { is given by }\\
&2 \ell=\frac{1}{2} \mathrm{at}^{2}\\
&20=\frac{1}{2}(10) \mathrm{t}^{2} \quad \mathrm{t}=2 \mathrm{sec}\\
&\overrightarrow{\mathrm{L}}=\mathrm{mvh} \hat{\mathrm{k}}=\text { math } \hat{\mathrm{k}}\\
&\overrightarrow{\mathrm{L}}=(0.2)(10) 2(1) \hat{\mathrm{k}}=4 \hat{\mathrm{k}} \text { [when particle passes through }(\ell,-\mathrm{h}) \text { ] }\\
&\vec{\tau}=\frac{\mathrm{d} \overrightarrow{\mathrm{L}}}{\mathrm{dt}}=\operatorname{mah} \hat{\mathrm{k}}=(0.2)(10)(1) \hat{\mathrm{k}}=2 \hat{\mathrm{k}} \text { (always) }
\end{aligned}$\\

Q14. Which of the following statement(s) is(are) correct about the spectrum of hydrogen atom?

(A) The ratio of the longest wavelength to the shortest wavelength in Balmer series is $9 / 5$

(B) There is an overlap between the wavelength ranges of Balmer and Paschen series.

(C) The wavelengths of Lyman series are given by $\left(1+\frac{1}{\mathrm{~m}^{2}}\right) \lambda_{0}$, where $\lambda_{0}$ is the shortest wavelength of Lyman series and $m$ is an integer

(D) The wavelength ranges of Lyman and Balmer series do not overlap

Answer: A & D

Q15. A long straight wire carries a current, $I=2$ ampere. A semi-circular conducting rod is placed beside it on two conducting parallel rails of negligible resistance. Both the rails are parallel to the wire. The wire, the rod, and the rails lie in the same horizontal plane, as shown in the figure. Two ends of the semi-circular rod are at distances $1 \mathrm{~cm}$ and $4 \mathrm{~cm}$ from the wire. At time $t=0$, the rod starts moving on the rails with a speed $v=3.0 \mathrm{~m} / \mathrm{s}$ (see the figure).
A resistor $\mathrm{R}=1.4 \Omega$ and a capacitor $\mathrm{C}_{0}=5.0 \mu \mathrm{F}$ are connected in series between the rails. At time $\mathrm{t}=0, \mathrm{C}_{0}$ is uncharged. Which of the following statement(s) is(are) correct?
$\left[\mu_{0}=4 \pi \times 10^{-7}\right.$ SI units. Take $\left.\ln 2=0.7\right]$

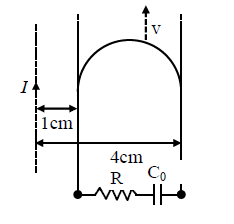
(A) Maximum current through $R$ is $1.2 \times 10^{-6}$ ampere

(B) Maximum current through $R$ is $3.8 \times 10^{-6}$ ampere

(D) Maximum charge on capacitor $\mathrm{C}_{0}$ is $2.4 \times 10^{-12}$ coulomb

Answer: A & C

Solution:

Emf induced across the semi-circular conducting rod.
$
\varepsilon=\int_{1}^{4} \frac{\mu_{0} I \mathrm{Idx}}{2 \pi \mathrm{x}}=\frac{\mu_{0} \mathrm{IV}}{2 \pi} \ln (4)=\frac{\mu_{0} \mathrm{IV}}{\pi} \ln (2)
$
Since the semi-circular conducting rod is moving with a constant speed $\mathrm{v}=3 \mathrm{~m} / \mathrm{s}$, then $\varepsilon=\frac{\mu_{0} I v}{\pi} \ln (2)=$ constant
The maximum current through the resistor $R$ is
$
\mathrm{i}_{\max }=\frac{\varepsilon}{\mathrm{R}}=\frac{\mu_{0} \mathrm{IV}}{\pi \mathrm{R}} \ln (2)=\frac{4 \times 10^{-7} \times 2 \times 3 \times 0.7}{1.4}=1.2 \times 10^{-6} \text { ampere. }
$
Maximum charge on the capacitor $\mathrm{C}_{0}$ is
$
\mathrm{q}_{\max }=\mathrm{C}_{0} \varepsilon=\mathrm{C}_{0}\left(\frac{\mu_{0} \mathrm{Iv}}{\pi} \ln (2)\right)=5 \times 10^{-6} \times 4 \times 10^{-7} \times 2 \times 3 \times 0.7=8.4 \times 10^{-12} \text { coulomb. }
$

Q16. A cylindrical tube, with its base as shown in the figure, is filled with water. It is moving down with a constant acceleration $a$ along a fixed inclined plane with angle $\theta=45^{\circ} . \mathrm{P}_{1}$ and $\mathrm{P}_{2}$ are pressures at points 1 and $\mathbf{2}$, respectively, located at the base of the tube. Let $\beta=\left(P_{1}-P_{2}\right) /(\rho g d)$, where $\rho$ is density of water, $d$ is the inner diameter of the tube and $g$ is the acceleration due to gravity. Which of the following statement(s) is(are) correct?

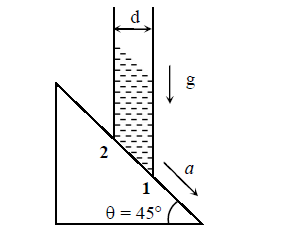
(A) $\beta=0$ when $a=\mathrm{g} / \sqrt{2}$

(B) $\beta>0$ when $a=\mathrm{g} / \sqrt{2}$

(D) $\beta=\frac{1}{\sqrt{2}}$ when $a=\mathrm{g} / 2$

Answer: A & C

Solution:

$\begin{aligned}
&\left(P_{1}-P_{2}\right) d s=\rho d s d \sqrt{2}(g \sin 45-a) \\
&\left(P_{1}-P_{2}\right)=\rho d(g-a \sqrt{2}) \\
&\beta=\frac{\left(P_{1}-P_{2}\right)}{\rho g d}=\left(1-\frac{a \sqrt{2}}{g}\right) \\
&\text { When } a=g / \sqrt{2}, \quad \beta=0 \\
&\text { When } a=g / 2, \quad \beta=\left(\frac{\sqrt{2}-1}{\sqrt{2}}\right)
\end{aligned}$

SECTION-4 : (Maximum Marks : 12)

This section contains three (03) questions.
The answer to each question is a non-negative integer.
For each question, enter the correct integer corresponding to the answer using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
Answer to each question will be evaluated according to the following marking scheme:
Full Marks: “+4” If only the correct integer is entered;
Zero Marks: “0” In all other cases

Q17. An $\alpha$-particle (mass $4 \mathrm{amu}$ ) and a singly charged sulfur ion (mass $32 \mathrm{amu}$ ) are initially at rest. They are accelerated through a potential $\mathrm{V}$ and then allowed to pass into a region of uniform magnetic field which is normal to the velocities of the particles. Within this region, the $\alpha$-particle and the sulfur ion move in circular orbits of radii $r_{\alpha}$ and $r_{s}$, respectively. The ratio $\left(r_{s} / r_{\alpha}\right)$ is __________.

Answer: 4

$\begin{aligned}
&\mathrm{r}_{\mathrm{a}}=\frac{\sqrt{2 \mathrm{~m}_{a} \mathrm{q}_{a} \mathrm{~V}}}{\mathrm{q}_{a} \mathrm{~B}} \\
&\mathrm{r}_{\mathrm{s}}=\frac{\sqrt{2 \mathrm{~m}_{\mathrm{s}} \mathrm{q}_{\mathrm{s}} \mathrm{V}}}{\mathrm{q}_{\mathrm{s}} \mathrm{B}} \\
&\frac{\mathrm{r}_{\mathrm{s}}}{\mathrm{r}_{\mathrm{a}}}=\sqrt{\frac{\mathrm{m}_{\mathrm{s}}}{\mathrm{q}_{\mathrm{s}}} \frac{\mathrm{q}_{a}}{\mathrm{~m}_{\alpha}}}=\sqrt{\left(\frac{32}{1}\right)\left(\frac{2}{4}\right)} \\
&\frac{\mathrm{r}_{\mathrm{s}}}{\mathrm{r}_{\mathrm{a}}}=4
\end{aligned}$

Q18. A thin rod of mass $M$ and length $a$ is free to rotate in the horizontal plane about a fixed vertical axis passing through point $\mathrm{O}$. A thin circular disc of mass $\mathrm{M}$ and of radius $a / 4$ is pivoted on this rod with its center at a distance $a / 4$ from the free end so that it can rotate freely about its vertical axis, as shown in the figure. Assume that both the rod and the disc have uniform density and they remain horizontal during the motion. An outside stationary observer finds the rod rotating with an angular velocity $\Omega$ and the disc rotating about its vertical axis with angular velocity $4 \Omega$. The total angular momentum of the system about the point $\mathrm{O}$ is $\left(\frac{\mathrm{M} a^{2} \Omega}{48}\right) \mathrm{n}$. The value of $\mathrm{n}$ is _________.

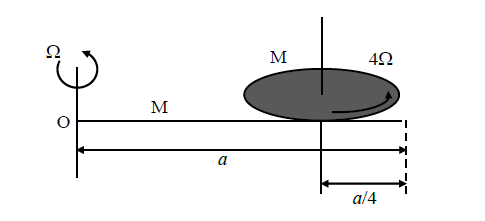
Answer: 49

Solution:

Angular momentum of disc about $\mathrm{O}$ is $\mathrm{L}_{\mathrm{DO}}=\mathrm{M}\left(\frac{3 \mathrm{a}}{4}\right)\left(\frac{3 \mathrm{a}}{4}\right) \Omega+\frac{\mathrm{M}}{2}\left(\frac{\mathrm{a}}{4}\right)^{2}(4 \Omega)$

Angular momentum of rod about $O$ is
$
\mathrm{L}_{\mathrm{RO}}=\frac{M \mathrm{a}^{2}}{3} \Omega
$
So, $\mathrm{L}_{0}=\mathrm{L}_{\mathrm{DO}}+\mathrm{L}_{\mathrm{RO}}=\frac{49}{48}\left(\mathrm{Ma}^{2} \Omega\right)$
Therefore, $n=49$

Q19. A small object is placed at the center of a large evacuated hollow spherical container. Assume that the container is maintained at $0 \mathrm{~K}$. At time $\mathrm{t}=0$, the temperature of the object is $200 \mathrm{~K}$. The temperature of the object becomes $100 \mathrm{~K}$ at $\mathrm{t}=\mathrm{t}_{1}$ and $50 \mathrm{~K}$ at $\mathrm{t}=\mathrm{t}_{2}$. Assume the object and the container to be ideal black bodies. The heat capacity of the object does not depend on temperature. The ratio $\left(\mathrm{t}_{2} / \mathrm{t}_{1}\right)$ is ________.

Answer: 9

Solution:

$\begin{aligned}
&-C \frac{\mathrm{dT}}{\mathrm{dt}}=\left(\mathrm{T}^{4}-\mathrm{T}_{\mathrm{S}}^{4}\right) \\
&\int_{200}^{100} \frac{\mathrm{dT}}{\mathrm{T}^{4}-\mathrm{T}_{\mathrm{S}}^{4}}=\int_{0}^{\mathrm{t}_{1}}-\frac{1}{\mathrm{c}} \mathrm{dt} \\
&-\frac{1}{3}\left[\frac{1}{\mathrm{~T}^{3}}\right]_{200}^{100}=-\frac{1}{\mathrm{c}}\left(\mathrm{t}_{1}\right) \\
&\Rightarrow\left[\frac{1}{(100)^{3}}-\frac{1}{(200)^{3}}\right]=\frac{3}{\mathrm{c}} \mathrm{t}_{1} \\
&\text { Similarly, }\left[\frac{1}{(50)^{3}}-\frac{1}{(200)^{3}}\right]=\frac{3}{\mathrm{c}} \mathrm{t}_{2} \\
&\frac{\mathrm{t}_{2}}{\mathrm{t}_{1}}=\frac{\left[\frac{1}{(50)^{3}}-\frac{1}{(200)^{3}}\right]}{\left[\frac{1}{(100)^{3}}-\frac{1}{(200)^{3}}\right]}=9
\end{aligned}$

Back to Lesson

Next Lesson