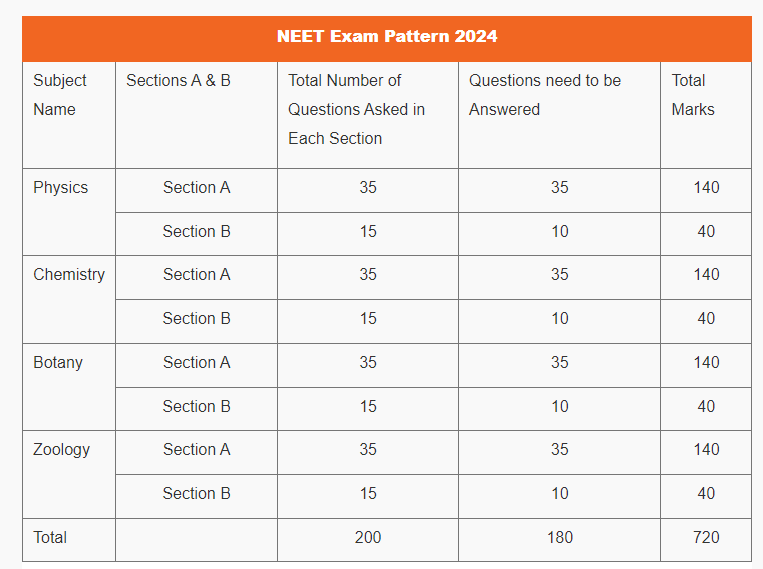
NEET Exam Pattern 2024
| Features | Highlights |
| Mode of Examination | Offline (Pen and Paper) |
| Questions Type | Multiple Choice Type |
| Total Questions in NEET 2024 | 200 (Students need to attempt 180 questions ) |
| Total Marks | 720 |
| NEET Exam Duration | 3 hours 20 minutes |
| NEET 2024 Marking Scheme |
|
| Medium of NEET 2024 Paper | English, Hindi, Assamese, Telugu, Bengali, Kannada, Marathi, Malayalam, Gujarati, Odia, Punjabi, Tamil, and Urdu |
| Questions will be asked from each section |
|
| Subjects | Physics, Biology, Chemistry |
NEET 2024 Exam Pattern: Subject Wise Marks Distribution
The purpose of your books is to get a good grasp on the concepts and fundamentals and will help you to build a strong foundation of understanding of the subjects. We recommend the following books and materials in addition to the course package we have put together for our NEET exam aspiring students.
Physics Books and Materials:
- Physics by NCERT
- Concept of Physics – H. C. Verma
- Objective Physics for NEET – D C Pandey
- Previous year papers (Any publication: Disha, MTG Objective, etc.)
NEET PHYSICS SYLLABUS
UNIT 1: PHYSICS AND MEASUREMENT
Units of measurements, System of Units, S I Units, fundamental and derived units, least count, significant figures, Errors in measurements, Dimensions of Physics quantities, dimensional analysis, and its applications.
UNIT 2: KINEMATICS
The frame of reference, motion in a straight line, Position- time graph, speed and velocity; Uniform and non-uniform motion, average speed and instantaneous velocity, uniformly accelerated motion, velocity-time, position-time graph, relations for uniformly accelerated motion, Scalars and Vectors, Vector. Addition and subtraction, scalar and vector products, Unit Vector, Resolution of a Vector. Relative Velocity, Motion in a plane, Projectile Motion, Uniform Circular Motion.
UNIT 3: LAWS OF MOTION
Force and inertia, Newton’s First law of motion; Momentum, Newton’s Second Law of motion, Impulses; Newton’s Third Law of motion. Law of conservation of linear momentum and its applications. Equilibrium of concurrent forces.
Static and Kinetic friction, laws of friction, rolling friction.
Dynamics of uniform circular motion: centripetal force and its applications: vehicle on a level circular road, vehicle on a banked road.
UNIT 4: WORK, ENERGY, AND POWER
Work done by a constant force and a variable force; kinetic and potential energies, work-energy theorem, power.
The potential energy of spring conservation of mechanical energy, conservative and nonconservative forces; motion in a vertical circle: Elastic and inelastic collisions in one and two dimensions.
UNIT5: ROTATIONAL MOTION
Centre of the mass of a two-particle system, Centre of the mass of a rigid body; Basic concepts of rotational motion; moment of a force; torque, angular momentum, conservation of angular momentum and its applications;
The moment of inertia, the radius of gyration, values of moments of inertia for simple geometrical objects, parallel and perpendicular axes theorems, and their applications. Equilibrium of rigid bodies, rigid body rotation and equations of rotational motion, comparison of linear and rotational motions.
UNIT 6: GRAVITATION
The universal law of gravitation. Acceleration due to gravity and its variation with altitude and depth. Kepler’s law of planetary motion. Gravitational potential energy; gravitational potential. Escape velocity, Motion of a satellite, orbital velocity, time period and energy of satellite.
UNIT 7: PROPERTIES OF SOLIDS AND LIQUIDS
Elastic behaviour, Stress-strain relationship, Hooke’s Law. Young’s modulus, bulk modulus, modulus of rigidity. Pressure due to a fluid column; Pascal’s law and its applications. Effect of gravity on fluid pressure.
Viscosity. Stokes’ law. terminal velocity, streamline, and turbulent flow.critical velocity. Bernoulli’s principle and its applications.
Surface energy and surface tension, angle of contact, excess of pressure across a curved surface, application of surface tension – drops, bubbles, and capillary rise. Heat, temperature, thermal expansion; specific heat capacity, calorimetry; change of state, latent heat. Heat transfer conduction, convection, and radiation.
UNIT 8: THERMODYNAMICS
Thermal equilibrium, zeroth law of thermodynamics, the concept of temperature. Heat, work, and internal energy. The first law of thermodynamics, isothermal and adiabatic processes.
The second law of thermodynamics: reversible and irreversible processes.
UNIT 9: KINETIC THEORY OF GASES
Equation of state of a perfect gas, work done on compressing a gas, Kinetic theory of gases assumptions, the concept of pressure. Kinetic interpretation of temperature: RMS speed of gas molecules: Degrees of freedom. Law of equipartition of energy and applications to specific heat capacities of gases; Mean free path. Avogadro’s number.
UNIT 10: OSCILLATIONS AND WAVES
Oscillations and periodic motion – time period, frequency, displacement as a function of time. Periodic functions. Simple harmonic motion (S.H.M.) and its equation; phase: oscillations of a spring -restoring force and force constant: energy in S.H.M. – Kinetic and potential energies; Simple pendulum – derivation of expression for its time period:
Wave motion. Longitudinal and transverse waves, speed of travelling wave. Displacement relation for a progressive wave. Principle of superposition of waves, reflection of waves. Standing waves in strings and organ pipes, fundamental mode and harmonics. Beats.
UNIT 11: ELECTROSTATICS
Electric charges: Conservation of charge. Coulomb’s law forces between two point charges, forces between multiple charges: superposition principle and continuous charge distribution.
Electric field: Electric field due to a point charge, Electric field lines. Electric dipole, Electric field due to a dipole. Torque on a dipole in a uniform electric field.
Electric flux. Gauss’s law and its applications to find field due to infinitely long uniformly charged straight wire uniformly charged infinite plane sheet, and uniformly charged thin spherical shell. Electric potential and its calculation for a point charge, electric dipole and system of charges; potential difference, Equipotential surfaces, Electrical potential energy of a system of two point charges and of electric dipole in an electrostatic field.
Conductors and insulators. Dielectrics and electric polarization, capacitors and capacitances, the combination of capacitors in series and parallel, and capacitance of a parallel plate capacitor with and without dielectric medium between the plates. Energy is stored in a capacitor.
UNIT 12: CURRENT ELECTRICITY
Electric current. Drift velocity, mobility and their relation with electric current.. Ohm’s law. Electrical resistance.. V-I characteristics of Ohmic and non-ohmic conductors. Electrical energy and power. Electrical resistivity and conductivity. Series and parallel combinations of resistors; Temperature dependence of resistance.
Internal resistance, potential difference and emf of a cell, a combination of cells in series and parallel. Kirchhoff’s laws and their applications. Wheatstone bridge. Metre Bridge.
UNIT 13: MAGNETIC EFFECTS OF CURRENT AND MAGNETISM
Biot – Savart law and its application to the current carrying circular loop. Ampere’s law and its applications to infinitely long current carrying straight wire and solenoid. Force on a moving charge in uniform magnetic and electric fields.
Force on a current-carrying conductor in a uniform magnetic field. The force between two parallel currents carrying conductors-definition of ampere. Torque experienced by a current loop in a uniform magnetic field: Moving coil galvanometer, its sensitivity, and conversion to ammeter and voltmeter.
Current loop as a magnetic dipole and its magnetic dipole moment. Bar magnet as an equivalent solenoid, magnetic field lines; Magnetic field due to a magnetic dipole (bar magnet) along its axis and perpendicular to its axis. Torque on a magnetic dipole in a uniform magnetic field. Para, dia- and ferromagnetic substances with examples, effect of temperature on magnetic properties.
UNIT 14: ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS
Electromagnetic induction: Faraday’s law. Induced emf and current: Lenz’s Law, Eddy currents. Self and mutual inductance. Alternating currents, peak and RMS value of alternating current/ voltage: reactance and impedance: LCR series circuit, resonance: power in AC circuits, wattles current. AC generator and transformer.
UNIT 15: ELECTROMAGNETIC WAVES
Displacement current. Electromagnetic waves and their characteristics, Transverse nature of electromagnetic waves, Electromagnetic spectrum (radio waves, microwaves, infrared, visible, ultraviolet. X-rays. Gamma rays), Applications of e.m. waves.
UNIT 16: OPTICS
Reflection of light, spherical mirrors, mirror formula. Refraction of light at plane and spherical surfaces, thin lens formula and lens maker formula. Total internal reflection and its applications.
Magnification. Power of a Lens. Combination of thin lenses in contact. Refraction of light through a prism. Microscope and Astronomical Telescope (reflecting and refracting ) and their magnifying powers.
Wave optics: wavefront and Huygens’ principle. Laws of reflection and refraction using Huygens principle. Interference, Young’s double-slit experiment and expression for fringe width, coherent sources, and sustained interference of light. Diffraction due to a single slit, width of central maximum.. Polarization, plane-polarized light: Brewster’s law, uses of plane-polarized light and Polaroid.
UNIT 17: DUAL NATURE OF MATTER AND RADIATION
Dual nature of radiation. Photoelectric effect. Hertz and Lenard’s observations; Einstein’s photoelectric equation: particle nature of light. Matter waves-wave nature of particle, de Broglie relation.
UNIT 18: ATOMS AND NUCLEI
Alpha-particle scattering experiment; Rutherford’s model of atom; Bohr model, energy levels, hydrogen spectrum. Composition and size of nucleus, atomic masses, Mass-energy relation, mass defect; binding energy per nucleon and its variation with mass number, nuclear fission, and fusion.
UNIT 19: ELECTRONIC DEVICES
Semiconductors; semiconductor diode: I-V characteristics in forward and reverse bias; diode as a rectifier; I-V characteristics of LED. the photodiode, solar cell, and Zener diode; Zener diode as a voltage regulator, Logic gates (OR. AND. NOT. NAND and NOR).
UNIT 20: EXPERIMENTAL SKILLS
Familiarity with the basic approach and observations of the experiments and activities:
- Vernier calipers-its use to measure the internal and external diameter and depth of a vessel.
- Screw gauge-its use to determine the thickness/ diameter of thin sheet/wire.
- Simple Pendulum-dissipation of energy by plotting a graph between the square of amplitude and time.
- Metre Scale – the mass of a given object by the principle of moments.
- Young’s modulus of elasticity of the material of a metallic wire.
- Surf ace tension of water by capillary rise and effect of detergents,
- Co-efficient of Viscosity of a given viscous liquid by measuring the terminal velocity of a given spherical body,
- Speed of sound in air at room temperature using a resonance tube,
- Specific heat capacity of a given (i) solid and (ii) liquid by method of mixtures.
- The resistivity of the material of a given wire using a metre bridge.
- The resistance of a given wire using Ohm’s law.
- Resistance and figure of merit of a galvanometer by half deflection method.
- The focal length of;
(i) Convex mirror
(ii) Concave mirror, and
(ii) Convex lens, using the parallax method. - The plot of the angle of deviation vs angle of incidence for a triangular prism.
- The refractive index of a glass slab using a travelling microscope.
- Characteristic curves of a p-n junction diode in forward and reverse bias.
- Characteristic curves of a Zener diode and finding reverse break down voltage.
- Identification of Diode. LED,. Resistor. A capacitor from a mixed collection of such items.
