Sample Quiz

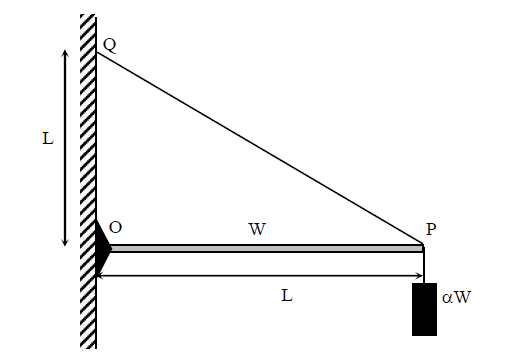
One end of a horizontal uniform beam of weight W and length L is hinged on a vertical wall at point \(O\) and its other end is supported by a light inextensible rope. The other end of the rope is fixed at point \(Q\), at a height \(L\) above the hinge at point O. A block of weight \(\alpha W\) is attached at the point \(P\) of the beam, as shown in the figure (not to scale). The rope can sustain a maximum tension of \((2 \sqrt{2}) \mathrm{W}\). Which of the following statement(s) is(are) correct?

A source, approaching with speed \(u\) towards the open end of a stationary pipe of length \(L\), is emitting a sound of frequency \(f_{5}\). The farther end of the pipe is closed. The speed of sound in air is \(v\) and \(f_{0}\) is the fundamental frequency of the pipe. For which of the following combination(s) of \(u\) and \(f_{S}\), will the sound reaching the pipe lead to a resonance?

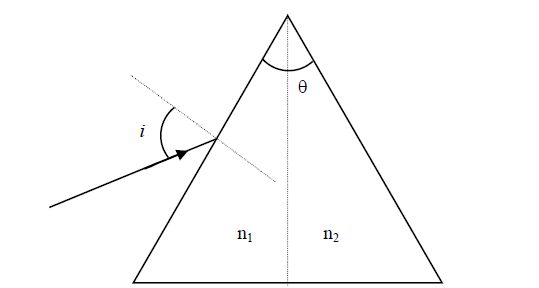
For a prism of prism angle \(\theta=60^{\circ}\), the refractive indices of the left half and the right half are, respectively, \(\mathrm{n}_{1}\) and \(\mathrm{n}_{2}\left(\mathrm{n}_{2} \geq \mathrm{n}_{1}\right)\) as shown in the figure. The angle of incidence \(i\) is chosen such that the incident light rays will have minimum deviation if \(\mathrm{n}_{1}=\mathrm{n}_{2}=\mathrm{n}=1.5\). For the case of unequal refractive indices, \(\mathrm{n}_{1}=\mathrm{n}  {\text {and} }  \mathrm{n}_{2}=\) \(\mathrm{n}+\Delta \mathrm{n}\) (where \(\Delta \mathrm{n} \ll<\mathrm{n}\) ), the angle of emergence \(e=i+\Delta e\). Which of the following statement(s) is(are) correct?

A physical quantity \(\overrightarrow{\mathrm{S}}\) is defined as \(\overrightarrow{\mathrm{S}}=(\overrightarrow{\mathrm{E}} \times \overrightarrow{\mathrm{B}}) / \mu_{0}\), where \(\overrightarrow{\mathrm{E}}\) is electric field, \(\overrightarrow{\mathrm{B}}\) is magnetic field and \(\mu_{0}\) is the permeability of free space. The dimensions of \(\overrightarrow{\mathrm{S}}\) are the same as the dimensions of which of the following quantity(ies)?

A heavy nucleus \(\mathrm{N}\), at rest, undergoes fission \(\mathrm{N} \rightarrow \mathrm{P}+\mathrm{Q}\), where \(\mathrm{P}\) and \(\mathrm{Q}\) are two lighter nuclei. Let \(\delta=M_{N}\) – \(\mathrm{M}_{\mathrm{P}}-\mathrm{M}_{\mathrm{Q}}\), where \(\mathrm{M}_{\mathrm{P}}, \mathrm{M}_{\mathrm{Q}}\) and \(\mathrm{M}_{\mathrm{N}}\) are the masses of \(P, Q\) and \(\mathrm{N}\), respectively. \(\mathrm{E}_{\mathrm{P}}\) and \(\mathrm{E}_{\mathrm{Q}}\) are the kinetic energies of \(P\) and \(Q\), respectively. The speeds of \(P\) and \(Q\) are \(v_{P}\) and \(v_{Q}\), respectively. If \(c\) is the speed of light, which of the following statement(s) is(are) correct?

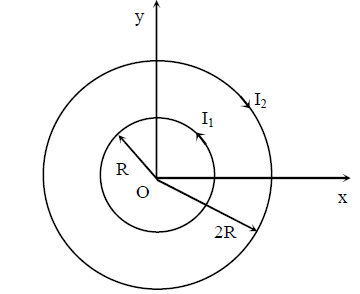
Two concentric circular loops, one of radius \(R\) and the other of radius \(2 R\), lie in the \(x y-p l a n e\) with the origin as their common center, as shown in the figure. The smaller loop carries current \(I_{1}\) in the anti-clockwise direction and the larger loop carries current \(\mathrm{I}_{2}\) in the clock wise direction, with \(\mathrm{I}_{2}>2 \mathrm{I}_{1} . \overrightarrow{\mathrm{B}}(\mathrm{x}, \mathrm{y})\) denotes the magnetic field at a point (x,y) in the \(x y-p l a n e .\) Which of the following statement(s) is(are) correct?

In the circuit, a metal filament lamp is connected in series with a capacitor of capacitance \(\mathrm{C} \mu \mathrm{F}\) across a \(200 \mathrm{~V}, 50\) Hz supply. The power consumed by the lamp is \(500 \mathrm{~W}\) while the voltage drop across it is \(100 \mathrm{~V}\). Assume that there is no inductive load in the circuit. Take RMS values of the voltages. The magnitude of the phase angle (in degrees) between the current and supply voltage is \(\phi .\) Assume, \(\pi \sqrt{3} \approx 5\).
The value of \(C\) is ______.

In the circuit, a metal filament lamp is connected in series with a capacitor of capacitance \(\mathrm{C} \mu \mathrm{F}\) across a \(200 \mathrm{~V}, 50\) Hz supply. The power consumed by the lamp is \(500 \mathrm{~W}\) while the voltage drop across it is \(100 \mathrm{~V}\). Assume that there is no inductive load in the circuit. Take RMS values of the voltages. The magnitude of the phase angle (in degrees) between the current and supply voltage is \(\phi .\) Assume, \(\pi \sqrt{3} \approx 5\).
The value of \(\phi\) is ______.

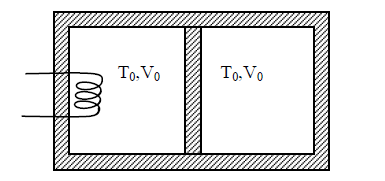
A thermally insulating cylinder has a thermally insulating and frictionless movable partition in the middle, as shown in the figure below. On each side of the partition, there is one mole of an ideal gas, with specific heat at constant volume, \(C_{V}=2 R\). Here, \(R\) is the gas constant. Initially, each side has a volume \(V_{0}\) and temperature \(T_{0}\). The left side has an electric heater, which is turned on at very low power to transfer heat \(Q\) to the gas on the left side. As a result, the partition moves slowly towards the right reducing the right side volume to \(V_{0} / 2\). Consequently, the gas temperatures on the left and the right sides become \(T_{L}\) and \(T_{R}\), respectively. Ignore the changes in the temperatures of the cylinder, heater, and the partition. The value of \(\frac{T_{R}}{T_{0}}\) is

A thermally insulating cylinder has a thermally insulating and frictionless movable partition in the middle, as shown in the figure below. On each side of the partition, there is one mole of an ideal gas, with specific heat at constant volume, \(C_{V}=2 R\). Here, \(R\) is the gas constant. Initially, each side has a volume \(V_{0}\) and temperature \(T_{0}\). The left side has an electric heater, which is turned on at very low power to transfer heat \(Q\) to the gas on the left side. As a result, the partition moves slowly towards the right reducing the right side volume to \(V_{0} / 2\). Consequently, the gas temperatures on the left and the right sides become \(T_{L}\) and \(T_{R}\), respectively. Ignore the changes in the temperatures of the cylinder, heater, and the partition. The value of \(\frac{Q}{\mathrm{RT}_{0}}\) is