Exemplar MCQs
Quiz Summary
0 of 43 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 43 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 43
1. Question
Which of the following sets cannot enter into the list of fundamental quantities in any system of units?
CorrectIncorrect -
Question 2 of 43
2. Question
A physical quantity is measured and the result is expressed as \(n u\) where \(u\) is the unit used and \(n\) is the numerical value. If the result is expressed in various units then
CorrectIncorrect -
Question 3 of 43
3. Question
Suppose a quantity \(x\) can be dimensionally represented in terms of \(\mathrm{M}, \mathrm{L}\) and \(\mathrm{T}\), that is, \([x]=\mathrm{M}^{a} \mathrm{~L}^{b} \mathrm{~T}^{c}\). The quantity mass
CorrectIncorrect -
Question 4 of 43
4. Question
A dimensionless quantity
CorrectIncorrect -
Question 5 of 43
5. Question
A unitless quantity
CorrectIncorrect -
Question 6 of 43
6. Question
\(
\int \frac{d x}{\sqrt{2 a x-x^{2}}}=a^{n} \sin ^{-1}\left[\frac{x}{a}-1\right] \text {. }
\)
The value of \(n\) isCorrectIncorrect -
Question 7 of 43
7. Question
The dimensions \(\mathrm{ML}^{-1} \mathrm{~T}^{-2}\) may correspond to
CorrectIncorrect -
Question 8 of 43
8. Question
Choose the correct statement(s):
CorrectIncorrect -
Question 9 of 43
9. Question
Choose the correct statement(s)
CorrectIncorrect -
Question 10 of 43
10. Question
\(\text { The volume of a cube of side } 1 \mathrm{~cm} \text { is equal to } \ldots . \mathrm{m}^{3}\)
CorrectIncorrect -
Question 11 of 43
11. Question
The surface area of a solid cylinder of radius \(2.0 \mathrm{~cm}\) and height \(10.0 \mathrm{~cm}\) is equal to … \((\mathrm{mm})^{2}\)
CorrectIncorrectHint
Surface area \(=2 \pi r h+2 \pi r^{2}=2 \pi r(h+r)\) \(=2 \times 22 / 7 \times 2 \times 10(10 \times 10+2 \times 10) \mathrm{mm}^{2}=1.5 \times 10^{4} \mathrm{~mm}^{2}\)
-
Question 12 of 43
12. Question
\(\text { A vehicle moving with a speed of } 18 \mathrm{~km} \mathrm{~h}^{-1} \text { covers….m in } 1 \mathrm{~s}\)
CorrectIncorrect -
Question 13 of 43
13. Question
\(\text { The relative density of lead is } 11.3 \text {. Its density is } \ldots . g \mathrm{~cm}^{-3} \text { or } \ldots . \mathrm{kg} \mathrm{} \mathrm{m}^{-3} \text {. }\)
CorrectIncorrectHint
Density \(=11.3 \mathrm{~g} \mathrm{~cm}^{-3}\)
\(
\begin{aligned}
&=11.3 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-3}\left[1 \mathrm{~kg}=10^{3} \mathrm{~g}, 1 \mathrm{~m}=10^{2} \mathrm{~cm}\right] \\
&=11.3 \times 10^{3} \mathrm{~kg} \mathrm{~m}^{-4}
\end{aligned}
\) -
Question 14 of 43
14. Question
\(1 \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-2}=\ldots \mathrm{~g} \mathrm{~cm}{ }^{2} \mathrm{~s}^{-2}\)
CorrectIncorrect -
Question 15 of 43
15. Question
\(1 \mathrm{~m}=\ldots \ldots \mathrm{ly}\)
CorrectIncorrectHint
\(1 \mathrm{~m} \quad=\frac{1}{9.46 \times 10^{5}} \mathrm{ly} \approx \frac{1}{10^{16}} \mathrm{ly}=10^{-16} \mathrm{ly}\)
-
Question 16 of 43
16. Question
\(G=6.67 \times 10^{-11} \mathrm{~N} \mathrm{~m}^{2}(\mathrm{~kg})^{-2}=\ldots .(\mathrm{cm})^{3} \mathrm{~s}^{-2} \mathrm{~g}^{-1}\)
CorrectIncorrectHint
\(G\)
\(
\begin{aligned}
&=6.67 \times 10^{-11} \mathrm{Nm}^{2} \mathrm{~kg}^{-2}=6.67 \times 10^{-11} \frac{\mathrm{kg} \mathrm{m}}{\mathrm{s}^{2}} \mathrm{~m}^{2} \mathrm{~kg}^{-2} \\
&=6.67 \times 10^{-11} \mathrm{~kg}^{-1} \mathrm{~m}^{3} \mathrm{~s}^{-2} \\
&=6.67 \times 10^{-11} \frac{\mathrm{m}^{3}}{\mathrm{~kg} \mathrm{~s}^{2}}=\frac{6.67 \times 10^{-11} \times\left(10^{2}\right)^{3}}{\left(10^{3}\right)^{2}} \\
&=6.67 \times 10^{-8} \mathrm{~cm}^{-3} \mathrm{~s}^{-2} \mathrm{~g}^{-1} .
\end{aligned}
\) -
Question 17 of 43
17. Question
A new unit of length is chosen such that the speed of light in vacuum is unity. What is the distance between the Sun and the Earth in terms of the new unit if light takes \(8 \mathrm{~min}\) and \(20 \mathrm{~s}\) to cover this distance?
CorrectIncorrectHint
Answer: Distance between Sun and Earth
= Speed of light in vacuum x time taken by light to travel from Sun to Earth \(=3 \times 10^{8} \mathrm{~m} / \mathrm{s} \times 8 \mathrm{~min} 20 \mathrm{~s}=3 \times\) \(10^{8} \mathrm{~m} / \mathrm{s} \times 500 \mathrm{~s}=500 \times 3 \times 10^{8} \mathrm{~m}\).
In the new system, the speed of light in vacuum is unity. So, the new unit of length is \(3 \times 10^{8} \mathrm{~m}\).
\(\therefore\) distance between Sun and Earth =500 new units. -
Question 18 of 43
18. Question
Which of the following is the most precise device for measuring length:
CorrectIncorrectHint
(a) Least count of vernier callipers \(=1 / 20=0.05 \mathrm{~mm}=5 \times 10^{-5} \mathrm{~m}\)
(b) Least count of screw gauge =Pitch/No. of divisions on circular scale \(=1 \times 10^{-3} / 100=1 \times 10^{-5} \mathrm{~m}\)
(c) Least count of optical instrument \(=6000 \mathrm{~A}\) (average wavelength of visible light as \(6000 \mathrm{~A})=6 \times 10^{-7} \mathrm{~m}\). As the least count of optical instrument is least, it is the most precise device out of three instruments given to us. -
Question 19 of 43
19. Question
A student measures the thickness of a human hair by looking at it through a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is \(3.5 \mathrm{~mm}\). What is the estimate of the thickness of the hair?
CorrectIncorrectHint
As magnification, \(m\) =thickness of image of hair/ real thickness of hair \(=100\) and average width of the image of hair as seen by microscope \(=3.5 \mathrm{~mm}\)
\(\therefore\) Thickness of hair \(=3.5 \mathrm{~mm} / 100=0.035 \mathrm{~mm}\) -
Question 20 of 43
20. Question
The photograph of a house occupies an area of \(1.75 \mathrm{~cm}^{2}\) on a \(35 \mathrm{~mm}\) slide. The slide is projected onto a screen, and the area of the house on the screen is \(1.55 \mathrm{~m}^{2}\). What is the linear magnification of the projector-screen arrangement.
CorrectIncorrectHint
Answer: Here area of the house on slide \(=1.75 \mathrm{~cm}^{2}=1.75 \times 10^{-4} \mathrm{~m}^{2}\) and area of the house of projector-
screen \(=1.55 \mathrm{~m}^{2}\)
\(\therefore\) Areal magnification =Area on screen/Area on slide \(=1.55 \mathrm{~m}^{2} / 1.75 \times 10^{-4} \mathrm{~m}^{2}=8.857 \times 10^{3}\)
\(\therefore\) Linear magnification
\(=\sqrt{\text { Areal magnification }}\)
\(
=\sqrt{(8.857) \times 10^{3}}
\)
\(
=94.1 \text {. }
\) -
Question 21 of 43
21. Question
A book with many printing errors contains four different formulas for the displacement \(y\) of a particle undergoing a certain periodic motion:
( \(a=\) maximum displacement of the particle, \(v=\) speed of the particle. \(T=\) time-period of motion). which formulas are wrong on dimensional grounds.
CorrectIncorrectHint
(a) \(y=a \sin \frac{2 \pi t}{T}\)
Here, \([L.H.S.]=[y]=[L]\)
and \([R.H.S.]=\left[a \sin \frac{2 \pi t}{T}\right]=\left[L \sin \frac{T}{T}\right]=[L]\)
So, it is correct.
(b) \(y=a \sin v t\)
Here, \([y]=[L]\) and \([a \sin v t]=\left[L \sin \left(L T^{-1} . T\right)\right]=[L \sin L]\) So, the equation is wrong.
(c) \(y=\left(\frac{a}{T}\right) \sin \frac{t}{a}\)
Here, \(\quad[y]=[L]\) and \(\left[\left(\frac{a}{T}\right) \sin \frac{t}{a}\right]=\left[\frac{L}{T} \sin \frac{T}{L}\right]=\left[L T^{-1} \sin T L^{-1}\right]\)
So, the equation is wrong.
(d) \(y=(a \sqrt{2})\left(\sin \frac{2 \pi t}{T}+\cos \frac{2 \pi t}{T}\right)\)
Here, \(\quad[y]=[L],[a \sqrt{2}]=[L]\)
and \(\left[\sin \frac{2 \pi t}{T}+\cos \frac{2 \pi t}{T}\right]=\left[\sin \frac{T}{T}+\cos \frac{T}{T}\right]=\) dimensionless. So, it is correct. -
Question 22 of 43
22. Question
The unit of length convenient on the atomic scale is known as an angstrom and is denoted by \(Å: 1 Å =10^{-10} \mathrm{~m}\). The size of a hydrogen atom is about \(0.5 \). What is the total atomic volume in \(\mathrm{m}^{3}\) of a mole of hydrogen atoms?
CorrectIncorrectHint
Volume of one hydrogen atom = \(\frac{4}{3} \pi r^{3}\) (volume of a sphere)
\(
=4 / 3 \times 3.14 \times\left(0.5 \times 10^{-10}\right) \mathrm{m}^{3}=5.23 \times 10^{-31} \mathrm{~m}^{3}
\)
According to Avagadro’s hypothesis, one mole of hydrogen contains \(6.023 \times 10^{23}\) atoms.
The atomic volume of 1 mole of hydrogen atoms
\(
=6.023 \times 1023 \times 5.23 \times 10^{-31}=3.15 \times 10^{-7} \mathrm{~m}^{3} \text {. }
\) -
Question 23 of 43
23. Question
The length, breadth, and thickness of a rectangular sheet of metal are \(4.234 \mathrm{~m}, 1.005 \mathrm{~m}\), and \(2.01 \mathrm{~cm}\) respectively. what is the area and volume of the sheet to correct significant figures?
CorrectIncorrectHint
As Area \(=(4.234 \times 1.005) \times 2=8.51034=8.5 \mathrm{~m}^{2}\)
\(
\text { Volume }=(4.234 \times 1.005) \times\left(2.01 \times 10^{-2}\right)=8.55289 \times 10^{-2}=0.0855 \mathrm{~m}^{3} \text {. }
\) -
Question 24 of 43
24. Question
A physical quantity \(P\) is related to four observables \(a, b, c\) and \(d\) as follows :
\(
P=a^{3} b^{2} /(\sqrt{c} d)
\)
The percentage errors of measurement in \(a, b, c\) and d are \(1 \%, 3 \%, 4 \%\) and \(2 \%\), respectively. What is the percentage error in the quantity \(P\) ? If the value of \(P\) calculated using the above relation turns out to be \(3.763\), to what value should you round off the result?CorrectIncorrectHint
As \(P=\frac{a^{3} b^{2}}{(\sqrt{c} d)}=a^{3} b^{2} c^{-1 / 2} d^{-1}\)
\(\therefore\) Maximum fractional error in the measurement
\(
\frac{\Delta P}{P}=3 \frac{\Delta a}{a}+2 \frac{\Delta b}{b}+\frac{1}{2} \frac{\Delta c}{c}+\frac{\Delta d}{d}
\)
As \(\quad \frac{\Delta a}{a}=1 \%, \quad \frac{\Delta b}{b}=3 \%, \quad \frac{\Delta c}{c}=4 \%\) and \(\frac{\Delta d}{d}=2 \%\)
\(\therefore\) Maximum fractional error in the measurement
\(
\begin{aligned}
\frac{\Delta P}{P} &=3 \times 1 \%+2 \times 3 \%+\frac{1}{2} \times 4 \%+2 \% \\
&=3 \%+6 \%+2 \%+2 \%=13 \%
\end{aligned}
\)
If \(P=3.763\), then \(\Delta P=13 \%\) of \(P\)
\(
=\frac{13 P}{100}=\frac{13 \times 3.763}{100}=0.489
\)
As the error lies in the first decimal place, the answer should be rounded off to the first decimal place. Hence, we shall express the value of \(P\) after rounding it off as \(P=3.8\). -
Question 25 of 43
25. Question
It is claimed that two cesium clocks if allowed to run for 100 years, free from any disturbance, may differ by only about \(0.02 \mathrm{~s}\). What does this imply for the accuracy of the standard cesium clock in measuring a time-interval of \(1 \mathrm{~s}\)?
CorrectIncorrectHint
Answer: Total time \(=100\) years \(=100 \times 365 \times 24 \times 60 \times 60 \mathrm{~s}\)
Error in 1 second \(=0.02 / 100 \times 365 \times 24 \times 60 \times 60\) \(=6.34 \times 10^{-12} \mathrm{~s}\)
\(\therefore\) Accuracy of 1 part in \(10^{11}\) to \(10^{12}\). -
Question 26 of 43
26. Question
The number of significant figures in 0.06900 is
CorrectIncorrectHint
Key concept: Significant figures in the measured value of a physical quantity tell the number of digits in which we have confidence. Larger the number of significant figures obtained in a measurement, greater is the accuracy of the measurement. The reverse is also true.
The following rules are observed in counting the number of significant figures in a given measured quantity.
1. All non-zero digits are significant.
2. A zero becomes significant figure if it appears between two non-zero digits.
3. Leading zeros or the zeros placed to the left of the number are never significant.
4. Trailing zeros or the zeros placed to the right of the number are significant.
5. In exponential notation, the numerical portion gives the number of significant figures.
Leading zeros or the zeros placed to the left of the number are never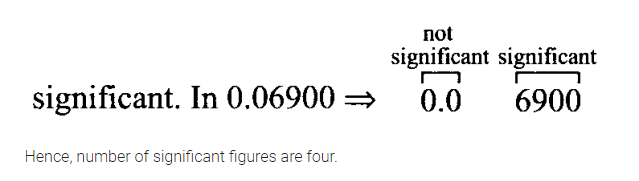
-
Question 27 of 43
27. Question
The sum of the numbers 436.32,227.2 and 0.301 in appropriate significant figures is
CorrectIncorrectHint
(b) The result of an addition or subtraction in the number having different precisions should be reported to the same number of decimal places as present in the number having the least number of decimal places.

The final result should, therefore, be rounded off to one decimal place, i.e. 664.
-
Question 28 of 43
28. Question
The mass and volume of a body are \(4.237 \mathrm{~g}\) and \(2.5 \mathrm{~cm}^3\), respectively. The density of the material of the body in correct significant figures is
CorrectIncorrectHint
(c) The answer to a multiplication or division is rounded off to the same number of significant figures as possessed by the least precise term used in the calculation. The final result should retain as many significant figures as are there in the original number with the least significant figures. In the given question, density should be reported to two significant figures
\(
\text { Density }=\frac{4.237 \mathrm{~g}}{2.5 \mathrm{~cm}^3}=1.6948
\)
After rounding off the number, we get density \(=1.7\) -
Question 29 of 43
29. Question
The numbers 2.745 and 2.735 on rounding off to 3 significant figures will give
CorrectIncorrectHint
Key concept: While rounding off measurements, we use the following rules by convention:
1. If the digit to be dropped is less than 5 , then the preceding digit is left unchanged.
2. If the digit to be dropped is more than 5, then the preceding digit is raised by one.
3. If the digit to be dropped is 5 followed by digits other than zero, then the preceding digit is raised by one.
4. If the digit to be dropped is 5 or 5 followed by zeros, then the preceding digit is left unchanged if it is even.
5. If the digit to be dropped is 5 or 5 followed by zeros, then the preceding digit is raised by one, if it is odd.
Units and Measurements
Let us round off 2.745 to 3 significant figures.
Here the digit to be dropped is 5 , then preceding digit is left unchanged, if it is even.
Hence on rounding off 2.745, it would be 2.74.
Now consider 2.737, here also the digit to be dropped is 5, then the preceding digit is raised by one, if it is odd. Hence on rounding off 2.735 to 3 significant figures, it would be 2.74. -
Question 30 of 43
30. Question
The length and breadth of a rectangular sheet are \(16.2 \mathrm{~cm}\) and \(10.1 \mathrm{~cm}\), respectively. The area of the sheet in appropriate significant figures and error is
CorrectIncorrectHint
Key concept: Error in product of quantities: Suppose \(x=a \times b\)
Let \(\Delta a=\) absolute error in measurement of \(a\),
\(\Delta b=\) absolute error in measurement of \(b\),
\(\Delta x=\) absolute error in calculation of \(x\), i.e. product of \(a\) and \(b\).
The maximum fractional error in \(x\) is \(\frac{\Delta x}{x}= \pm\left(\frac{\Delta a}{a}+\frac{\Delta b}{b}\right)\)
Percentage error in the value of \(x=(\) Percentage error in value of \(a)+\)
(Percentage error in value of \(b\) )
According to the problem, length \(l=(16.2 \pm 0.1) \mathrm{cm}\)
Breadth \(b=(10.1 \pm 0.1) \mathrm{cm}\)
Area \(A=l \times b=(16.2 \mathrm{~cm}) \times(10.1 \mathrm{~cm})=163.62 \mathrm{~cm}^2\)
As per the rule area will have only three significant figures and error will have only one significant figure. Rounding off we get, area \(A=164 \mathrm{~cm}^2\)
If \(\Delta A\) is error in the area, then relative error is calculated as \(\frac{\Delta A}{A}\).
\(
\begin{aligned}
\frac{\Delta A}{A}=\frac{\Delta l}{l}+\frac{\Delta b}{b} & =\frac{0.1 \mathrm{~cm}}{16.2 \mathrm{~cm}}+\frac{0.1 \mathrm{~cm}}{10.1 \mathrm{~cm}} \\
& =\frac{1.01+1.62}{16.2 \times 10.1}=\frac{2.63}{163.62} \\
\Rightarrow \Delta A & =A \times \frac{2.63}{163.62} \mathrm{~cm}^2=163.62 \times \frac{2.63}{163.62}=2.63 \mathrm{~cm}^2
\end{aligned}
\)
\(\Delta A=3 \mathrm{~cm}^2\) (By rounding off to one significant figure)
Area, \(A=A \pm \Delta A=(164 \pm 3) \mathrm{cm}^2\) -
Question 31 of 43
31. Question
Which of the following pairs of physical quantities does not have same dimensional formula?
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Work }=F \times \Delta x=\left[M L T^{-2}\right][L]=\left[M L^2 T^{-2}\right] \\
& \text { Torque = force } \times \text { distance }=\left[M L^2 T^{-2}\right] \\
& \text { Angular momentum }=m v r=[M]\left[L T^1\right][L]=\left[M L^2 T^{-1}\right] \\
& \text { Planck’s constant }=\frac{E}{V}=\frac{\left[M L^2 T^{-2}\right]}{\left[T^{-1}\right]}=\left[M L^2 T^{-1}\right]
\end{aligned}
\)
(b) Angular momentum \(=\operatorname{mvr}=[M]\left[L T^1\right][L]=\left[M L^2 T^{-1}\right]\)
Planck’s constant \(=\frac{E}{V}=\frac{\left[M L^2 T^{-2}\right]}{\left[T^{-1}\right]}=\left[M L^2 T^{-1}\right]\)
(c) Tension (force) \(=\left[M L T^{-2}\right]\)
Surface tension \(=\frac{\text { force }}{\text { length }}=\frac{\left[M L T^{-2}\right]}{[L]}=\left[M L^0 T^{-2}\right]\)
(d) Impulse \(=F \times \Delta t=\left[M L T^{-2}\right][T]=\left[M L T^{-1}\right]\)
Momentum \(=\) mass \(\times\) velocity \(=[M]\left[L T^{-1}\right]=\left[M L T^{-1}\right]\)
So, among the above pairs only tension and surface tension does not have same dimensional formula. They both sound similar but they both have different meaning and different applications. -
Question 32 of 43
32. Question
Measure of two quantitles along with the precision of respective measuring instrument is
\(
\begin{aligned}
& A=2.5 \mathrm{~m} \mathrm{~s}^{-1} \pm 0.5 \mathrm{~m} \mathrm{~s}^{-1} \\
& B=0.10 \mathrm{~s} \pm 0.01 \mathrm{~s}
\end{aligned}
\)
The value of \(A B\) will beCorrectIncorrectHint
(a) According to the problem,
\(
\begin{aligned}
A & =2.5 \mathrm{~ms}^{-1} \pm 0.5 \mathrm{~ms}^{-1}, B=0.10 \mathrm{~s} \pm 0.01 \mathrm{~s} \\
Z & =A B=(2.5)(0.10)=0.25 \mathrm{~m} \\
\frac{\Delta Z}{Z} & =\frac{\Delta A}{A}+\frac{\Delta B}{B}, \Delta Z=Z\left(\frac{\Delta A}{A}+\frac{\Delta B}{B}\right) \\
& =0.25\left(\frac{0.5}{2.5}+\frac{0.01}{0.10}\right)=0.25(0.2+0.1)=0.075 \\
\Delta Z & =0.075=0.08 \mathrm{~m} \quad \text { (rounding off to two significant figures.) }
\end{aligned}
\)
Thus, measured value of \(A B\), i.e., \(=Z \pm \Delta Z=(0.25 \pm 0.08) \mathrm{m}\) -
Question 33 of 43
33. Question
You measure two quanttles as \(A=1.0 \mathrm{~m} \pm 0.2 \mathrm{~m}, B=2.0 \mathrm{~m} \pm 0.2 \mathrm{~m}\). We should report correct value for \(\sqrt{\mathrm{AB}}\) as:
CorrectIncorrectHint
(d) According to the problem, \(A=1.0 \mathrm{~m} \pm 0.2 \mathrm{~m}, B=2.0 \mathrm{~m} \pm 0.2 \mathrm{~m}\)
Let, \(Z=\sqrt{A B}=\sqrt{(1.0)(2.0)}=1.414 \mathrm{~m}\)
Rounding off to two significant digits \(Z=1.4 \mathrm{~m}\)
As
\(
\begin{aligned}
\frac{\Delta Z}{Z} & =\frac{1}{2} \frac{\Delta A}{A}+\frac{1}{2} \frac{\Delta B}{B} \\
& =\frac{1}{2}\left(\frac{0.2 \mathrm{~m}}{1 \mathrm{~m}}\right)+\frac{1}{2}\left(\frac{0.2 \mathrm{~m}}{2 \mathrm{~m}}\right)=0.15
\end{aligned}
\)
\(
\Rightarrow \Delta Z=Z(0.15)=1.4 \mathrm{~m}(0.15)=0.212
\)
Rounding off to one significant digit, \(\Delta Z=0.2 \mathrm{~m}\)
The correct value for \(\sqrt{A B}=1.4 \pm 0.2 \mathrm{~m}\). -
Question 34 of 43
34. Question
Which of the following measurements is most precise?
CorrectIncorrectHint
Key concept: Precision is the degree to which several measurements provide answers very close to each other. It is an indicator of the scatter in the data. The lesser the scatter, the higher the precision. Let us first check the units. In all the options magnitude is the same but the units of measurement are different. As here \(5.00 \mathrm{~mm}\) has the smallest unit. All given measurements are correct up to two decimal places. However, the absolute error in (a) is \(0.01 \mathrm{~mm}\) which is the least of all the four. So it is most precise.
-
Question 35 of 43
35. Question
The mean length of an object is \(5 \mathrm{~cm}\). Which of the following measurements is most accurate?
CorrectIncorrectHint
Key concept: Accuracy describes the nearness of a measurement to the standard or true value, i.e. a highly accurate measuring device will provide measurements very close to the standard, true or known values. Example: In target shooting, a high score indicates the nearness to the bull’s eye and is a measure of the shooter’s accuracy.
According to the problem, length \(l=5 \mathrm{~cm}\)
Let us first check the errors in each values by picking options one by one, we get
\(
\begin{array}{ll}
\Delta l_1=5-4.9=0.1 \mathrm{~cm}, & \Delta l_2=5-4.805=0.195 \mathrm{~cm}, \\
\Delta l_3=5.25-5=0.25 \mathrm{~cm} \text { and } & \Delta l_4=5.4-5=0.4 \mathrm{~cm}
\end{array}
\)
Error \(\Delta l_1\) is the least.
Hence \(4.9 \mathrm{~cm}\) is most closer to true value. So, 4.9 is more accurate. -
Question 36 of 43
36. Question
Youngs modulus of steel is \(1.9 \times 10^{11} \mathrm{~N} / \mathrm{m}^2\). When expressed in CGS units of dynes \(/ \mathrm{cm}^2\), it will be equal to \(\left(1 \mathrm{~N}=10^5\right.\) dyne, \(1 \mathrm{~m}^2=10^4 \mathrm{~cm}^2\) )
CorrectIncorrectHint
(c) According to the problem,
Young’s modulus, \(Y=1.9 \times 10^{11} \mathrm{~N} / \mathrm{m}^2\)
\(1 \mathrm{~N}\) in SI system of units \(=10^5\) dyne in C.G.S system.
Hence, \(\quad Y=1.9 \times 10^{11} \times 10^5\) dyne \(/ \mathrm{m}^2\)
In C.G.S. length is measured in unit ‘ \(\mathrm{cm}\) ‘, so we should also convert \(\mathrm{m}\) into \(\mathrm{cm}\).
\(
\begin{aligned}
\therefore \quad Y & =1.9 \times 10^{11}\left(\frac{10^5 \text { dyne }}{10^4 \mathrm{~cm}^2}\right) \quad[\because 1 \mathrm{~m}=100 \mathrm{~cm}] \\
& =1.9 \times 10^{12} \text { dyne } / \mathrm{cm}^2
\end{aligned}
\) -
Question 37 of 43
37. Question
If momentum \((P)\), area \((A)\) and time \((T)\) are taken to be fundamental quantities, then energy has the dimensional formula
CorrectIncorrectHint
(d) According to the problem, fundamental quantities are momentum \((p)\), area \((A)\), and time \((T)\) and we have to express energy in these fundamental quantities.
Let energy \(E\),
\(
E \propto p^a A^A T^c \Rightarrow E=k p^a A^A T^c
\)
where, \(k\) is dimensionless constant of proportionality.
Dimensional formula of energy, \([E]=\left[M L^2 T^{-2}\right]\) and \([p]=\left[M L T^{-1}\right]\)
\(
[A]=\left[L^2\right],[T]=[T] \text { and }[E]=[K][p]^a[A]^b[T]^c
\)
Putting all the dimensions, we get
\(
\begin{aligned}
M L^2 T^{-2} & =\left[M L T^{-1}\right]^a\left[L^2\right]^b[T]^c \\
& =M^a L^{a+2 b} T^{-a+c}
\end{aligned}
\)
According to the principle of homogeneity of dimensions, we get
\(
\begin{aligned}
& a=1 \dots(i) \\
& a+2 b=2 \dots(ii) \\
& -a+c=-2 \dots(iii)
\end{aligned}
\)
By solving these equations (i), (ii) and (iii), we get
\(
a=1, b=\frac{1}{2}, c=-1
\)
Dimensional formula for \(E\) is \(\left[p^1 A^{1 / 2} t^{-1}\right]\). -
Question 38 of 43
38. Question
On the basis of dimensions, decide which of the following relations for the displacement of a particle undergoing simple harmonic motion is not correct:
CorrectIncorrectHint
(b, c) The argument of trigonometric functions (sin, cos etc.) should be dimensionless. \(y\) is displacement and according to the principle of homogeneity of dimensions LHS and RHS.
\(
\begin{aligned}
& {[Y]=[L],[a]=[L]} \\
& {\left[\frac{2 \pi t}{T}\right]=\frac{[T]}{[T]}=\left[T^0\right]} \\
& {[v t]=[v][t]=\left[L T^{-1}\right][T]=[L]} \\
& {\left[\frac{a}{T}\right]=\frac{[a]}{[T]}=\frac{[L]}{[T]}=\left[L T^{-1}\right]} \\
& {\left[\frac{t}{a}\right]=\left[L^{-1} T\right]} \\
& {[\text { LHS }] \neq[\text { RHS }]}
\end{aligned}
\)
Hence, (c) is not the correct option. \(\Rightarrow\) LHS \(\neq\) RHS.
So, option (b) is also not correct. -
Question 39 of 43
39. Question
If \(P, Q, R\) are physical quantities, having different dimensions, which of the following combinations can never be a meaningful quantity?
CorrectIncorrectHint
\((a, e)\)
Key concept: Principle of Homogeneity of dimensions: It states that in a correct equation, the dimensions of each term added or subtracted must be same. Every correct equation must have same dimensions on both sides of the equation.
According to the problem \(P, Q\) and \(R\) are having different dimensions, since, sum and difference of physical dimensions, are meaningless, i.e., \((P-Q)\) and \((R+Q)\) are not meaningful.
So in option (b) and (c), PQ may have the same dimensions as those of \(R\) and in option (d) \(P R\) and \(Q^2\) may have same dimensions as those of \(R\).
Hence, they cannot be added or subtracted, so we can say that (a) and (e) are not meaningful. -
Question 40 of 43
40. Question
Photon is quantum of radiation with energy \(E=h v\) where \(v\) is frequency and \(h\) is Planck’s constant. The dimensions of \(h\) are the same as that of
CorrectIncorrectHint
(b, d) We know that energy of radiation, \(E=h v\). So, we have to compare \(h\) with dimensional formula of each option.
\(
\begin{aligned}
{[h] } & =\frac{[E]}{[v]}=\frac{\text { force } \times \text { displacement }}{\text { frequency }} \\
& =\frac{\left[M L^2 T^{-2}\right]}{\left[T^{-1}\right]}=\left[M L^2 T^{-1}\right]
\end{aligned}
\)
(a) Dimension of linear impulse
\(
[I]=[F t]=\left[M L T^{-2}\right][T]=\left[M L T^{-1}\right]
\)
where, \(t\) is the time interval.
(b) Dimension of angular impulse
\(
[J]=[I \omega]=\left[M L^2\right]\left[T^{-1}\right]=\left[M L^2 T^{-1}\right]
\)
(c) Dimensión of linear momentum
\(
[P]=[m v]=[M]\left[L T^{-1}\right]=\left[M L T^{-1}\right]
\)
(d) Dimension of angular momentum
\(
[L]=[m v r]=[M]\left[L T^{-1}\right][L]=\left[M L^2 T^{-1}\right]
\)
Hence, the dimension of angular impulse and angular momentum is the same as Planck’s constant \((h)\). -
Question 41 of 43
41. Question
If Planck’s constant \((h)\) and speed of light in vacuum \((c)\) are taken as two fundamental quantities, which one of the following can, in addition, be taken to express length, mass and time in terms of the three chosen fundamental quantities?
CorrectIncorrectHint
(a, b, d) We know that dimension of \(h\)
\(
[h]=\frac{\left[M L^2 T^{-2}\right]}{\left[T^{-1}\right]}=\left[M L^2 T^{-1}\right],[G]=\left[M^{-1} L^3 T^{-2}\right],[c]=\left[L T^{-1}\right]
\)
For mass, let \(m=c^a h^b G^c\) where \(a, b\) and \(c\) are exponents of \(c, h\) and \(G\) respectively.
\(
\Rightarrow \quad\left[M L^0 T^0\right]=\left[L T^{-1}\right]^a\left[M L^2 T^{-1}\right]^b\left[M^{-1} L^3 T^{-2}\right]^c
\)
Using the principle of homogeneity of dimensions,
\(
\begin{aligned}
& b-c=1 \dots(i) \\
& a+2 b+3 c=0 \dots(ii) \\
& -a-b-2 c=0 \dots(iii)
\end{aligned}
\)
Adding eqns. (i), (ii) and (iii),
\(
2 b=1 \Rightarrow b=1 / 2
\)
From eqn. (i), \(a=b-1=\frac{1}{2}-1=-\frac{1}{2}\)
From eqn. (iii), \(a=-(b+2 c)=-\left(\frac{1}{2}-1\right)=\frac{1}{2}\)
Hence, \(m=c^{1 / 2} h^{1 / 2} G^{-1 / 2} \Rightarrow m=\sqrt{\frac{c h}{G}}\)
Similarly, for length, \(L=\sqrt{\frac{h G}{c^3}}\) and for time, \(T=\sqrt{\frac{h G}{c^5}}\)
\(\therefore\) Planck’s length \(=\sqrt{\frac{G h}{c^3}} ;\) Planck’s time \(=\sqrt{\frac{G h}{c^5}}\);
and Planck’s mass \(=\sqrt{\frac{c h}{G}}\)
Mass can be expressed by \(m_e\) and \(m_p\).
Hence, (a), (b) or (d) any can be used to express \(L, M\) and \(T\) in terms of three chosen fundamental quantities. -
Question 42 of 43
42. Question
Which of the following ratios express pressure?
CorrectIncorrectHint
\((a, b)\) Let us first express the relation of pressure with other physical quantities one by one with the help of dimensional analysis.
We know that pressure
(a) \(\frac{\text { Force }}{\text { Area }}=\frac{\left[M L T^{-2}\right]}{\left[L^2\right]}=\left[M L^{-1} T^{-2}\right]\)
So, this ratio express pressure (In fact this ratio actually represents pressure).
(b) \(\frac{\text { Energy }}{\text { Area }}=\frac{\left[M L^2 T^{-2}\right]}{\left[L^2\right]}=\left[M T^{-2}\right]\)
Dimensions of this ratio are not same as pressure, so this ratio does not express pressure.
(c) \(\frac{\text { Energy }}{\text { Volume }}=\frac{\left[M L^2 T^{-2}\right]}{\left[L^3\right]}=\left[M L^{-1} T^{-2}\right]\)
Dimensions of this ratio is the same as pressure, so this ratio also express pressure.
(d) \(\frac{\text { Force }}{\text { Volume }}=\frac{\left[M L T^{-2}\right]}{\left[L^3\right]}=\left[M L^{-2} T^{-2}\right]\)
Dimensions of this ratio are not same as pressure, so this ratio does not express pressure. -
Question 43 of 43
43. Question
Which of the following are not a unit of time?
CorrectIncorrectHint
(b, d) Parsec and light year are those practical units which are used to measure large distances. For example, the distance between sun and earth or other celestial bodies. So they are the units of length not time. Here, second and year represent time.
Important point: 1 light year (distance that light travels in 1 year with speed \(=3 \times 10^8 \mathrm{~m} / \mathrm{s}\).) \(=9.46 \times 10^{11} \mathrm{~m}\) And 1 par see \(=3.08 \times 10^{16} \mathrm{~m}\)