Circular Motion

Vehicle on a leveled circular road

When a vehicle travels in a curved path, there must be a centripetal force acting on it. This centripetal force is provided by the frictional force between tyre and surface of the road. Consider a vehicle of mass ‘ \(m\) ‘ moving at a speed ‘ \(v\) ‘ in the circular track of radius ‘ \(R\) ‘. There are three forces acting on the vehicle when it moves as shown in the Figure 3.43

• Gravitational force \((\mathrm{mg})\) acting downwards
• Normal force \((\mathrm{mg})\) acting upwards
• Frictional force \(\left(\mathrm{F}_{\mathrm{s}}\right)\) acting horizontally inwards along the road.

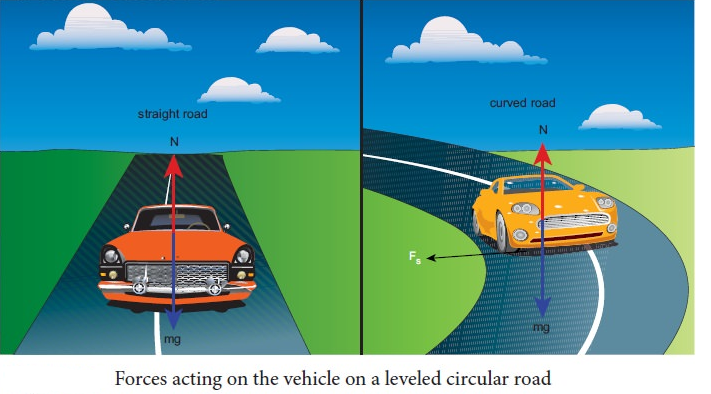
Suppose the road is horizontal then the normal force and gravitational force are exactly equal and opposite. The centripetal force is provided by the force of static friction \(F_S\) between the tyre and surface of the road which acts towards the center of the circular track,
\(
\frac{m v^2}{R}=F_s
\)

As we have already seen in the previous section, the static friction can increase from zero to a maximum value
\(
F_s \leq \mu_s m g .
\)

There are two conditions possible:
Safe Turn: If \(\frac{m v^2}{R} \leq \mu_s m g\), or \(\mu_s \geq \frac{v^2}{R g}\) or \(\sqrt{\mu_s R g} \geq v\)
The static friction would be able to provide necessary centripetal force to bend the car on the road. So the coefficient of static friction between the tyre and the surface of the road determines what maximum speed the car can have for safe turn.
Skid:  If \(\frac{m v^2}{R}>\mu_s m g\), or \(\mu_s<\frac{v^2}{R g}\) (skid)
If the static friction is not able to provide enough centripetal force to turn, the vehicle will start to skid.

Motion of a car on a banked road

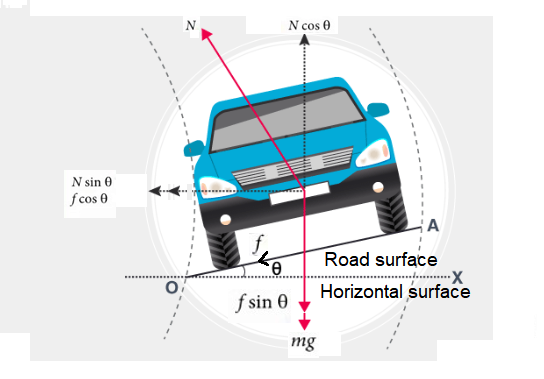
Component of friction force \((f \cos \theta)\) and component of normal reaction \((N \sin \theta)\) provide required centripetal force for safe turning.
The maximum permissible speed to avoid slipping
\(
v_{\max }=\left[\frac{R g\left(\mu_s+\tan \theta\right)}{1-\mu_s \tan \theta}\right]^{1 / 2}
\)

If road is smooth then \(\mu_s=0\) and \(v_{\max }=\sqrt{R g \tan \theta}\)
For a car taking a circular turn on a horizontal road, the centripetal force is provided by the force of friction.

Motion of a car on a level road
Friction force \(\left(\mu_s N\right)\) between tyres and road provides a required centripetal force.
\(
f \leq \mu_s N=\frac{m v^2}{R}
\)

Maximum speed of car for safe turning, \(v=\sqrt{\mu_s R g}\)