7.16 Problems on Rotational Mechanics

Q1: A wheel rotates with a constant acceleration of \(2.0 \mathrm{rad} / \mathrm{s}^2\). If the wheel starts from rest, how many revolutions will it make in the first 10 seconds?

Answer:

The angular displacement in the first 10 seconds is given by
\(
\theta=\omega_0 t+\frac{1}{2} \alpha t^2=\frac{1}{2}\left(2.0 \mathrm{rad} / \mathrm{s}^2\right)(10 \mathrm{~s})^2=100 \mathrm{rad} .
\)
As the wheel turns by \(2 \pi\) radian in each revolution, the number of revolutions in \(10 \mathrm{~s}\) is
\(
n=\frac{100}{2 \pi}=16
\)

Q2: The wheel of a motor, accelerated uniformly from rest, rotates through 2.5 radian during the first second. Find the angle rotated during the next second.

Answer: As the angular acceleration is constant, we have
\(
\theta=\omega_0 t+\frac{1}{2} \alpha t^2=\frac{1}{2} \alpha t^2 .
\)
Thus, \(\quad 2 \cdot 5 \mathrm{rad}=\frac{1}{2} \alpha(1 \mathrm{~s})^2\)
\(
\alpha=5 \mathrm{rad} / \mathrm{s}^2
\)
or, \(\quad \alpha=5 \mathrm{rad} / \mathrm{s}^2\).
The angle rotated during the first two seconds is
\(
=\frac{1}{2} \times\left(5 \mathrm{rad} / \mathrm{s}^2\right)(2 \mathrm{~s})^2=10 \mathrm{rad} \text {. }
\)
Thus, the angle rotated during the 2nd second is
\(
10 \mathrm{rad}-2.5 \mathrm{rad}=7.5 \mathrm{rad} \text {. }
\)

Q3: A wheel having moment of inertia \(2 \mathrm{~kg}-\mathrm{m}^2\) about its axis, rotates at \(50 \mathrm{rpm}\) about this axis. Find the torque that can stop the wheel in one minute.

Answer: The initial angular velocity
\(
=50 \mathrm{rpm}=\frac{5 \pi}{3} \mathrm{rad} / \mathrm{s} \text {. }
\)
Using \(\omega=\omega_0+\alpha t\),
\(
\alpha=\frac{\omega-\omega_0}{t}=\frac{0-\frac{5 \pi}{3}}{60} \mathrm{rad} / \mathrm{s}^2=-\frac{\pi}{36} \mathrm{rad} / \mathrm{s}^2 .
\)
The torque that can produce this deceleration is
\(
\Gamma=I|\alpha|=\left(2 \mathrm{~kg}-\mathrm{m}^2\right)\left(\frac{\pi}{36} \mathrm{rad} / \mathrm{s}^2\right)=\frac{\pi}{18} \mathrm{~N}-\mathrm{m} .
\)

Q4: A string is wrapped around the rim of a wheel of moment of inertia \(0.20 \mathrm{~kg}-\mathrm{m}^2\) and radius \(20 \mathrm{~cm}\). The wheel is free to rotate about its axis. Initially, the wheel is at rest. The string is now pulled by a force of \(20 \mathrm{~N}\). Find the angular velocity of the wheel after \(5 \cdot 0\) seconds.

Answer: 

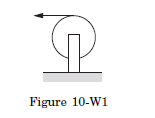
The torque applied to the wheel is
\(
\Gamma=F \cdot r=(20 \mathrm{~N})(0.20 \mathrm{~m})=4.0 \mathrm{~N-m}.
\)
The angular acceleration produced is
\(
\alpha=\frac{\Gamma}{I}=\frac{4.0 \mathrm{~N}-\mathrm{m}}{0.20 \mathrm{~kg}-\mathrm{m}^2}=20 \mathrm{rad} / \mathrm{s}^2 .
\)
The angular velocity after 5.0 seconds is
\(
\omega=\omega_0+\alpha t=\left(20 \mathrm{rad} / \mathrm{s}^2\right)(5 \cdot 0 \mathrm{~s})=100 \mathrm{rad} / \mathrm{s} .
\)

Q5: A wheel of radius \(r\) and moment of inertia \(I\) about its axis is fixed at the top of an inclined plane of inclination \(\theta\) as shown in figure (10-W2). A string is wrapped round the wheel and its free end supports a block of mass \(M\) which can slide on the plane. Initially, the wheel is rotating at a speed \(\omega\) in a direction such that the block slides up the plane. How far will the block move before stopping?

Answer: Suppose the deceleration of the block is \(a\). The linear deceleration of the rim of the wheel is also \(a\). The angular deceleration of the wheel is \(\alpha=a / r\). If the tension in the string is \(T\), the equations of motion are as follows:
\(
\begin{aligned}
& M g \sin \theta-T=M a \\
& T r=I \alpha=I a / r .
\end{aligned}
\)
and
\(
\operatorname{Tr}=I \alpha=I a / r \text {. }
\)
Eliminating \(T\) from these equations,
giving,
\(
\begin{aligned}
& M g \sin \theta-I \frac{a}{r^2}=M a \\
& a=\frac{M g r^2 \sin \theta}{I+M r^2} .
\end{aligned}
\)
The initial velocity of the block up the incline is \(v=\omega r\). Thus, the distance moved by the block before stopping is
\(
x=\frac{v^2}{2 a}=\frac{\omega^2 r^2\left(I+M r^2\right)}{2 M g r^2 \sin \theta}=\frac{\left(I+M r^2\right) \omega^2}{2 M g \sin \theta} .
\)

Q6: The pulley shown in figure (10-W3) has a moment of inertia \(I\) about its axis and its radius is \(R\). Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.

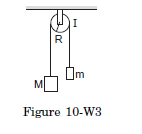
Answer: Suppose the tension in the left string is \(T_1\) and that in the right string is \(T_2\). Suppose the block of mass \(M\) goes down with an acceleration \(a\) and the other block moves up with the same acceleration. This is also the tangential acceleration of the rim of the wheel as the string does not slip over the rim. The angular acceleration of the wheel is, therefore, \(\alpha=a / R\). The equations of motion for the mass \(M\), the mass \(m\) and the pulley are as follows:
\(
\begin{gathered}
M g-T_1=M a \dots(i)\\
T_2-m g=m a \dots(ii)
\end{gathered}
\)
\(
T_1 R-T_2 R=I \alpha=I a / R \dots(iii)
\)
Putting \(T_1\) and \(T_2\) from (i) and (ii) into (iii),
\(
[M(g-a)-m(g+a)] R=I \frac{a}{R}
\)
which gives \(a=\frac{(M-m) g R^2}{I+(M+m) R^2}\).

Q7: Two small kids weighing \(10 \mathrm{~kg}\) and \(15 \mathrm{~kg}\) respectively are trying to balance a seesaw of total length \(5.0 \mathrm{~m}\), with the fulcrum at the centre. If one of the kids is sitting at an end, where should the other sit?

Answer: It is clear that the \(10 \mathrm{~kg}\) kid should sit at the end and the \(15 \mathrm{~kg}\) kid should sit closer to the centre. Suppose his distance from the centre is \(x\). As the kids are in equilibrium, the normal force between a kid and the seesaw equals the weight of that kid. Considering the rotational equilibrium of the seesaw, the torques of the forces acting on it should add to zero. The forces are (a) (15 kg)g downward by the \(15 \mathrm{~kg}\) kid,
(b) \((10 \mathrm{~kg}) \mathrm{g}\) downward by the \(10 \mathrm{~kg}\) kid,
(c) weight of the seesaw and
(d) the normal force by the fulcrum.
Taking torques about the fulcrum,
\(
\begin{aligned}
(15 \mathrm{~kg}) g x & =(10 \mathrm{~kg}) g(2.5 \mathrm{~m}) \\
x & =1.7 \mathrm{~m} .
\end{aligned}
\)

Q8: A uniform ladder of mass \(10 \mathrm{~kg}\) leans against a smooth vertical wall making an angle of \(53^{\circ}\) with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder.

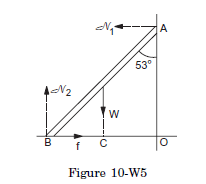
Answer: The forces acting on the ladder are shown in figure (10-W5). They are
(a) its weight \(W\),
(b) normal force \(\mathcal{N}_1\) by the vertical wall,
(c) normal force \(\mathcal{N}_2\) by the floor and
(d) frictional force \(f\) by the floor.
Taking horizontal and vertical components
\(
\begin{array}{ll}
& \mathcal{N}_1=f \dots(i)\\
\text { and } & \mathcal{N}_2=W \dots(ii)
\end{array}
\)
Taking torque about \(B\),
\(
\mathcal{N}_1(A O)=W(C B)
\)
\(
\text { or, } \quad \quad \mathcal{N}_1(A B) \cos 53^{\circ}=W \frac{A B}{2} \sin 53^{\circ}
\)
\(
\text { or, } \quad \quad \mathcal{N}_1 \frac{3}{5}=\frac{W}{2} \frac{4}{5}
\)
\(
\text { or, } \quad \quad \mathcal{N}_1=\frac{2}{3} W \dots(iii)
\)
The normal force by the floor is
\(
\mathcal{N}_2=W=(10 \mathrm{~kg})\left(9 \cdot 8 \mathrm{~m} / \mathrm{s}^2\right)=98 \mathrm{~N} \text {. }
\)
The frictional force is
\(
f= \mathcal{N}_1=\frac{2}{3} W=65 \mathrm{~N} .
\)

Q9: The ladder shown in figure (10-W6) has negligible mass and rests on a frictionless floor. The crossbar connects the two legs of the ladder at the middle. The angle between the two legs is \(60^{\circ}\). The fat person sitting on the ladder has a mass of \(80 \mathrm{~kg}\). Find the contact force exerted by the floor on each leg and the tension in the crossbar.

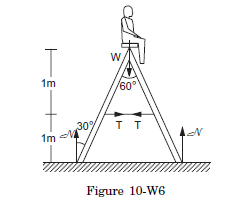
Answer: The forces acting on different parts are shown in figure (10-W6). Consider the vertical equilibrium of “the ladder plus the person” system. The forces acting on this system are its weight \((80 \mathrm{~kg}) \mathrm{g}\) and the contact force \(\mathcal{N}+\mathcal{N}=2 \mathcal{N}\) due to the floor. Thus,
\(
\begin{aligned}
2 \mathcal{N} & =(80 \mathrm{~kg}) g \\
\mathcal{N} & =(40 \mathrm{~kg})\left(9.8 \mathrm{~m} / \mathrm{s}^2\right)=392 \mathrm{~N} .
\end{aligned}
\)
or,
Next, consider the equilibrium of the left leg of the ladder. Taking torques of the forces acting on it about the upper end,
\(
\begin{aligned}
& \mathcal{N}(2 \mathrm{~m}) \tan 30^{\circ}=T(1 \mathrm{~m}) \\
& T=\mathcal{N} \frac{2}{\sqrt{3}}=(392 \mathrm{~N}) \times \frac{2}{\sqrt{3}} \approx 450 \mathrm{~N} .
\end{aligned}
\)

Q10: Two small balls \(A\) and \(B\), each of mass \(m\), are attached rigidly to the ends of a light rod of length \(d\). The structure rotates about the perpendicular bisector of the rod at an angular speed \(\omega\). Calculate the angular momentum of the individual balls and of the system about the axis of rotation.

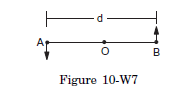
Answer: Consider the situation shown in Figure (10-W7). The velocity of the ball \(A\) with respect to the centre \(O\) is \(v=\frac{\omega d}{2}\). The angular momentum of the ball with respect to the axis is \(L_1=m v r=m\left(\frac{\omega d}{2}\right)\left(\frac{d}{2}\right)=\frac{1}{4} m \omega d^2\).
The same is the angular momentum \(L_2\) of the second ball. The angular momentum of the system is equal to the sum of these two angular momenta i.e., \(L=\frac{1}{2} m \omega d^2\).

Q11: Two particles of mass \(m\) each are attached to a light rod of length \(d\), one at its centre and the other at a free end. The rod is fixed at the other end and is rotated in a plane at an angular speed \(\omega\). Calculate the angular momentum of the particle at the end with respect to the particle at the centre.

Answer:

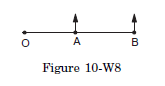
The situation is shown in Figure (10-W8). The velocity of the particle \(A\) with respect to the fixed end \(O\) is \(v_A=\omega\left(\frac{d}{2}\right)\) and that of \(B\) with respect to \(O\) is \(v_B=\omega d\). Hence the velocity of \(B\) with respect to \(A\) is \(v_B-v_A=\omega\left(\frac{d}{2}\right)\). The angular momentum of \(B\) with respect to \(A\) is, therefore,
\(
L=m v r=m \omega\left(\frac{d}{2}\right) \frac{d}{2}=\frac{1}{4} m \omega d^2
\)
along the direction perpendicular to the plane of rotation.

Q12: A particle is projected at time \(t=0\) from a point \(P\) with a speed \(v_0\) at an angle of \(45^{\circ}\) to the horizontal. Find the magnitude and the direction of the angular momentum of the particle about the point \(P\) at time \(t=v_0 / g\).

Answer: Let us take the origin at \(P, X\)-axis along the horizontal and \(Y\)-axis along the vertically upward direction as shown in figure (10-W9). For horizontal motion during the time 0 to \(t\),

\(
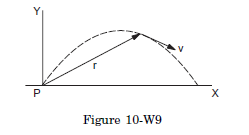
\begin{aligned}
& v_x=v_0 \cos 45^{\circ}=v_0 / \sqrt{ } 2 \\
& \text { and } \quad x=v_x t=\frac{v_0}{\sqrt{2}} \cdot \frac{v_0}{g}=\frac{v_0^2}{\sqrt{ } 2 g} \text {. } \\
&
\end{aligned}
\)
For vertical motion,
\(
v_y=v_0 \sin 45^{\circ}-g t=\frac{v_0}{\sqrt{ } 2}-v_0=\frac{(1-\sqrt{ } 2)}{\sqrt{ } 2} v_0
\)
\(
\text { and } \quad \begin{aligned}
y & =\left(v_0 \sin 45^{\circ}\right) t-\frac{1}{2} g t^2 \\
& =\frac{v_0^2}{\sqrt{2} g}-\frac{v_0^2}{2 g}=\frac{v_0^2}{2 g}(\sqrt{ } 2-1)
\end{aligned}
\)
The angular momentum of the particle at time \(t\) about the origin is
\(
\begin{aligned}
L & =\vec{r} \times \vec{p}=m \vec{r} \times \vec{v} \\
& =m(\overrightarrow{i x}+\overrightarrow{j y}) \times\left(\vec{i} v_x+\vec{j} v_y\right)
\end{aligned}
\)
\(
\begin{aligned}
& =m\left(\vec{k} x v_y-\vec{k} y v_x\right) \\
& =m \vec{k}\left[\left(\frac{v_0^2}{\sqrt{2} g}\right) \frac{v_0}{\sqrt{2}}(1-\sqrt{2})-\frac{v_0^2}{2 g}(\sqrt{2}-1) \frac{v_0}{\sqrt{2}}\right]
\end{aligned}
\)
\(
=-\vec{k} \frac{m v_0^3}{2 \sqrt{2} g}
\)
Thus, the angular momentum of the particle is \(\frac{m v_0^3}{2 \sqrt{2} g}\) in the negative \(Z\)-direction, i.e., perpendicular to the plane of motion, going into the plane.

Q13: A uniform circular disc of mass \(200 \mathrm{~g}\) and radius \(4.0 \mathrm{~cm}\) is rotated about one of its diameter at an angular speed of \(10 \mathrm{rad} / \mathrm{s}\). Find the kinetic energy of the disc and its angular momentum about the axis of rotation.

Answer: The moment of inertia of the circular disc about its diameter is
\(
\begin{aligned}
I & =\frac{1}{4} M r^2=\frac{1}{4}(0.200 \mathrm{~kg})(0.04 \mathrm{~m})^2 \\
& =8.0 \times 10^{-5} \mathrm{~kg}-\mathrm{m}^2 .
\end{aligned}
\)
The kinetic energy is
\(
\begin{aligned}
K & =\frac{1}{2} I \omega^2=\frac{1}{2}\left(8 \cdot 0 \times 10^{-5} \mathrm{~kg}-\mathrm{m}^2\right)\left(100 \mathrm{rad}^2 / \mathrm{s}^2\right) \\
& =4 \cdot 0 \times 10^{-3} \mathrm{~J}
\end{aligned}
\)
and the angular momentum about the axis of rotation is
\(
L=I \omega=\left(8.0 \times 10^{-5} \mathrm{~kg}-\mathrm{m}^2\right)(10 \mathrm{rad} / \mathrm{s})
\)
\(
=8.0 \times 10^{-4} \mathrm{~kg}-\mathrm{m}^2 / \mathrm{s}=8.0 \times 10^{-4} \mathrm{~J}-\mathrm{s} .
\)

Q14: A wheel rotating at an angular speed of \(20 \mathrm{rad} / \mathrm{s}\) is brought to rest by a constant torque in 4.0 seconds. If the moment of inertia of the wheel about the axis of rotation is \(0.20 \mathrm{~kg}-\mathrm{m}^2\), find the work done by the torque in the first two seconds.

Answer: The angular deceleration of the wheel during the 4.0 seconds may be obtained by the equation
\(
\begin{aligned}
\omega & =\omega_0-\alpha t \\
\alpha & =\frac{\omega_0-\omega}{t}=\frac{20 \mathrm{rad} / \mathrm{s}}{4.0 \mathrm{~s}}=5.0 \mathrm{rad} / \mathrm{s}^2 .
\end{aligned}
\)
The torque applied to produce this deceleration is
\(
\Gamma=I \alpha=\left(0.20 \mathrm{~kg}-\mathrm{m}^2\right)\left(5.0 \mathrm{rad} / \mathrm{s}^2\right)=1.0 \mathrm{~N}-\mathrm{m} .
\)
The angle rotated in the first two seconds is
\(
\theta=\omega_0 t-\frac{1}{2} \alpha t^2
\)
\(
\begin{aligned}
& =(20 \mathrm{rad} / \mathrm{s})(2 \mathrm{~s})-\frac{1}{2}\left(5 \cdot 0 \mathrm{rad} / \mathrm{s}^2\right)\left(4 \cdot 0 \mathrm{~s}^2\right) \\
& =40 \mathrm{rad}-10 \mathrm{rad}=30 \mathrm{rad} .
\end{aligned}
\)
The work done by the torque in the first 2 seconds is, therefore,
\(
W=\Gamma \theta=(1.0 \mathrm{~N}-\mathrm{m})(30 \mathrm{rad})=30 \mathrm{~J} .
\)

Q15: Two masses \(M\) and \(m\) are connected by a light string going over a pulley of radius \(r\). The pulley is free to rotate about its axis which is kept horizontal. The moment of inertia of the pulley about the axis is I. The system is released from rest. Find the angular momentum of the system when the mass \(M\) has descended through a height h. The string does not slip over the pulley.

Answer: 

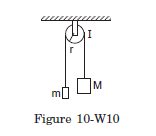
The situation is shown in Figure (10-W10). Let the speed of the masses be \(v\) at time \(t\). This will also be the speed of a point on the rim of the wheel and hence the angular velocity of the wheel at time \(t\) will be \(v / r\). If the height descended by the mass \(M\) is \(h\), the loss in the potential energy of the “masses plus the pulley” system is \(M g h-m g h\). The gain in kinetic energy is
\(
\frac{1}{2} M v^2+\frac{1}{2} m v^2+\frac{1}{2} I\left(\frac{v}{r}\right)^2 \text {. As no energy is lost, }
\)
\(
\frac{1}{2}\left(M+m+\frac{I}{r^2}\right) v^2=(M-m) g h
\)
\(
\text { or, } \quad v^2=\frac{2(M-m) g h}{M+m+\frac{I}{r^2}} \text {. }
\)
The angular momentum of the mass \(M\) is \(M v r\) and that of the mass \(m\) is \(m v r\) in the same direction. The angular momentum of the pulley is \(I \omega=I v / r\). The total angular momentum is
\(
\begin{aligned}
{\left[(M+m) r+\frac{I}{r}\right] v } & =\left[\left(M+m+\frac{I}{r^2}\right) r\right] \sqrt{\frac{2(M-m) g h}{M+m+\frac{I}{r^2}}} \\
& =\sqrt{2(M-m)\left(M+m+\frac{I}{r^2}\right) r^2 g h}
\end{aligned}
\)

Q16: Figure (10-W11) shows a mass \(m\) placed on a frictionless horizontal table and attached to a string passing through a small hole in the surface. Initially, the mass moves in a circle of radius \(r_0\) with a speed \(v_0\) and the free end of the string is held by a person. The person pulls on the string slowly to decrease the radius of the circle to \(r\). (a) Find the tension in the string when the mass moves in the circle of radius \(r\). (b) Calculate the change in the kinetic energy of the mass.

Answer: The torque acting on the mass \(m\) about the vertical axis through the hole is zero. The angular momentum about this axis, therefore, remains constant. If the speed of the mass is \(v\) when it moves in the circle of radius \(r\), we have
\(
m v_0 r_0=m v r
\)
or,
\(
v=\frac{r_0}{r} v_0 \dots(i)
\)
(a) The tension \(T=\frac{m v^2}{r}=\frac{m r_0^2 v_0^2}{r^3}\).
(b) The change in kinetic energy \(=\frac{1}{2} m v^2-\frac{1}{2} m v_0^2\).
By (i), it is \(\frac{1}{2} m v_0^2\left[\frac{r_0^2}{r^2}-1\right]\).

Q17: A uniform rod of mass \(m\) and length \(l\) is kept vertical with the lower end clamped. It is slightly pushed to let it fall down under gravity. Find its angular speed when the rod is passing through its lowest position. Neglect any friction at the clamp. What will be the linear speed of the free end at this instant?

Answer:

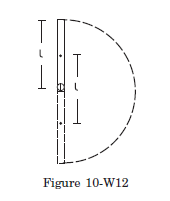
As the rod reaches its lowest position, the centre of mass is lowered by a distance \(l\). Its gravitational potential energy is decreased by \(\mathrm{mgl}\). As no energy is lost against friction, this should be equal to the increase in the kinetic energy. As the rotation occurs about the horizontal axis through the clamped end, the moment of inertia is \(I=m l^2 / 3\). Thus,
\(
\begin{aligned}
\frac{1}{2} I \omega^2 & =m g l \\
\frac{1}{2}\left(\frac{m l^2}{3}\right) \omega^2 & =m g l \\
\omega & =\sqrt{\frac{6 g}{l} .}
\end{aligned}
\)
The linear speed of the free end is
\(
v=l \omega=\sqrt{6 g l} .
\)

Q18: Four particles each of mass \(m\) are kept at the four corners of a square of the edge \(a\). Find the moment of inertia of the system about a line perpendicular to the plane of the square and passing through the centre of the square.

Answer:

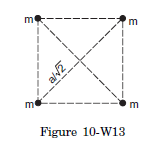
The perpendicular distance of every particle from the given line is \(a / \sqrt{2}\). The moment of inertia of one particle is, therefore, \(m(a / \sqrt{ } 2)^2=\frac{1}{2} m a^2\). The moment of inertia of the system is, therefore, \(4 \times \frac{1}{2} m a^2=2 m a^2\).

Q19: Two identical spheres each of mass \(1.20 \mathrm{~kg}\) and radius \(10.0 \mathrm{~cm}\) are fixed at the ends of a light rod so that the separation between the centres is \(50^{\circ} 0 \mathrm{~cm}\). Find the moment of inertia of the system about an axis perpendicular to the rod passing through its middle point.

Answer: 

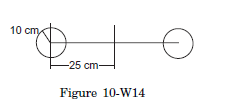
Consider the diameter of one of the spheres parallel to the given axis. The moment of inertia of this sphere about the diameter is
\(
\begin{aligned}
I & =\frac{2}{5} m R^2=\frac{2}{5}(1.20 \mathrm{~kg})(0.1 \mathrm{~m})^2 \\
& =4.8 \times 10^{-3} \mathrm{~kg}-\mathrm{m}^2 .
\end{aligned}
\)
Its moment of inertia about the given axis is obtained by using the parallel axes theorem. Thus,
\(
\begin{aligned}
I & =I_{c m}+m d^2 \\
& =4.8 \times 10^{-3} \mathrm{~kg}-\mathrm{m}^2+(1.20 \mathrm{~kg})(0.25 \mathrm{~m})^2 \\
& =4.8 \times 10^{-3} \mathrm{~kg}-\mathrm{m}^2+0.075 \mathrm{~kg}-\mathrm{m}^2 \\
& =79.8 \times 10^{-3} \mathrm{~kg}-\mathrm{m}^2 .
\end{aligned}
\)
The moment of inertia of the second sphere is also the same so that the moment of inertia of the system is
\(
2 \times 79.8 \times 10^{-3} \mathrm{~kg}-\mathrm{m}^2 \approx 0.160 \mathrm{~kg}-\mathrm{m}^2 .
\)

Q20: Two uniform identical rods each of mass \(M\) and length \(l\) are joined to form a cross as shown in figure (10-W15). Find the moment of inertia of the cross about a bisector as shown dotted in the figure.

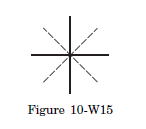
Answer: Consider the line perpendicular to the plane of the figure through the centre of the cross. The moment of inertia of each rod about this line is \(\frac{M l^2}{12}\) and hence the moment of inertial of the cross is \(\frac{M l^2}{6}\). The moment of inertia of the cross about the two bisectors are equal by symmetry and according to the theorem of perpendicular axes, the moment of inertia of the cross about the bisector is \(\frac{M l^2}{12}\).

Q21: A uniform rod of mass \(M\) and length a lies on a smooth horizontal plane. A particle of mass \(m\) moving at a speed \(v\) perpendicular to the length of the rod strikes it at a distance a \(/ 4\) from the centre and stops after the collision. Find (a) the velocity of the centre of the rod and (b) the angular velocity of the rod about its centre just after the collision.

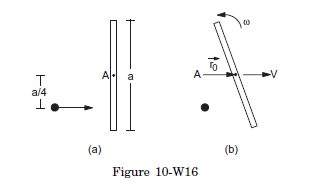
Answer: The situation is shown in Figure (10-W16a). Consider the rod and the particle together as the system. As there is no external resultant force, the linear momentum of the system will remain constant. Also there is no resultant external torque on the system and so the angular momentum of the system about any line will remain constant.
Suppose the velocity of the centre of the rod is \(V\) and the angular velocity about the centre is \(\omega\).
(a) The linear momentum before the collision is \(m v\) and that after the collision is \(M V\). Thus,
\(
m v=M V, \text { or } V=\frac{m}{M} v .
\)
(b) Let \(A\) be the centre of the rod when it is at rest. Let \(A B\) be the line perpendicular to the plane of the figure. Consider the angular momentum of “the rod plus the particle” system about \(A B\). Initially, the rod is at rest. The angular momentum of the particle about \(A B\) is
\(
L=m v(a / 4) .
\)
After the collision, the particle comes to rest. The angular momentum of the rod about \(A\) is
\(
\vec{L}=\vec{L}_{\mathrm{cm}}+M \overrightarrow{r_0} \times \vec{V} .
\)
As \(\quad \overrightarrow{r_0} \| \vec{V}, \quad \overrightarrow{r_0} \times \vec{V}=0\).
Thus,
\(
\vec{L}=\vec{L}_{\mathrm{cm}}
\)
Hence the angular momentum of the rod about \(A B\) is
\(
L=I \omega=\frac{M a^2}{12} \omega .
\)
Thus, \(\quad \frac{m v a}{4}=\frac{M a^2}{12} \omega \quad\) or, \(\omega=\frac{3 m v}{M a}\).

Q22: A wheel of perimeter \(220 \mathrm{~cm}\) rolls on a level road at a speed of \(9 \mathrm{~km} / \mathrm{h}\). How many revolutions does the wheel make per second?

Answer: As the wheel rolls on the road, its angular speed \(\omega\) about the centre and the linear speed \(v\) of the centre are related as \(v=\omega r\).
\(
\begin{aligned}
\therefore \omega & =\frac{v}{r}=\frac{9 \mathrm{~km} / \mathrm{h}}{220 \mathrm{~cm} / 2 \pi}=\frac{2 \pi \times 9 \times 10^5}{220 \times 3600} \mathrm{rad} / \mathrm{s} . \\
& =\frac{900}{22 \times 36} \mathrm{rev} / \mathrm{s}=\frac{25}{22} \mathrm{rev} / \mathrm{s} .
\end{aligned}
\)

Q23: A cylinder is released from rest from the top of an incline of inclination \(\theta\) and length \(l\). If the cylinder rolls without slipping, what will be its speed when it reaches the bottom?

Answer: Let the mass of the cylinder be \(m\) and its radius \(r\). Suppose the linear speed of the cylinder when it reaches the bottom is \(v\). As the cylinder rolls without slipping, its angular speed about its axis is \(\omega=v / r\). The kinetic energy at the bottom will be
\(
\begin{aligned}
K & =\frac{1}{2} I \omega^2+\frac{1}{2} m v^2 \\
& =\frac{1}{2}\left(\frac{1}{2} m r^2\right) \omega^2+\frac{1}{2} m v^2=\frac{1}{4} m v^2+\frac{1}{2} m v^2=\frac{3}{4} m v^2 .
\end{aligned}
\)
This should be equal to the loss of potential energy \(m g l \sin \theta\). Thus, \(\quad \frac{3}{4} m v^2=m g l \sin \theta\) or,
\(
v=\sqrt{\frac{4}{3} g l \sin \theta} .
\)

Q24: A sphere of mass \(m\) rolls without slipping on an inclined plane of inclination \(\theta\). Find the linear acceleration of the sphere and the force of friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?

Answer:

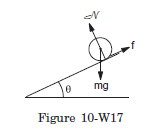
Suppose the radius of the sphere is \(r\). The forces acting on the sphere are shown in Figure (10-W17). They are (a) weight \(m g\), (b) normal force \(\mathcal{N}\) and (c) friction \(f\).

Let the linear acceleration of the sphere down the plane be \(a\). The equation for the linear motion of the centre of mass is
\(
m g \sin \theta-f=m a \dots(i)
\)
As the sphere rolls without slipping, its angular acceleration about the centre is \(a / r\). The equation of rotational motion about the centre of mass is,
\(
\begin{aligned}
f r & =\left(\frac{2}{5} m r^2\right)\left(\frac{a}{r}\right) \\
f & =\frac{2}{5} m a \dots(ii)
\end{aligned}
\)
From (i) and (ii),
\(
\begin{aligned}
a & =\frac{5}{7} g \sin \theta \\
\text { and } \quad f & =\frac{2}{7} m g \sin \theta .
\end{aligned}
\)
The normal force is equal to \(m g \cos \theta\) as there is no acceleration perpendicular to the incline. The maximum friction that can act is, therefore, \(\mu m g \cos \theta\), where \(\mu\) is the coefficient of static friction. Thus, for pure rolling \(\mu m g \cos \theta>\frac{2}{7} m g \sin \theta\)
or, \(\mu>\frac{2}{7} \tan \theta\).

Q25: Figure (10-W18) shows two cylinders of radii \(r_1\) and \(r_2\) having moments of inertia \(I_1\) and \(I_2\) about their respective axes. Initially, the cylinders rotate about their axes with angular speeds \(\omega_1\) and \(\omega_2\) as shown in the figure. The cylinders are moved closer to touch each other keeping the axes parallel. The cylinders first slip over each other at the contact but the slipping finally ceases due to the friction between them. Find the angular speeds of the cylinders after the slipping ceases.

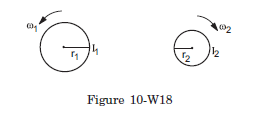
Answer: When slipping ceases, the linear speeds of the points of contact of the two cylinders will be equal. If \(\omega_1^{\prime}\) and \(\omega_2^{\prime}\) be the respective angular speeds, we have
\(
\omega_1^{\prime} r_1=\omega_2^{\prime} r_2 \dots(i)
\)
The change in the angular speed is brought about by the frictional force which acts as long as the slipping exists. If this force \(f\) acts for a time \(t\), the torque on the first cylinder is \(f r_1\) and that on the second is \(f r_2\). Assuming \(\omega_1 r_1>\omega_2 r_2\), the corresponding angular impluses are \(-f r_1 t\) and \(f r_2 t\). We, therefore, have
\(
\begin{aligned}
-f r_1 t & =I_1\left(\omega_1^{\prime}-\omega_1\right) \\
\text { and } \quad f r_2 t & =I_2\left(\omega_2^{\prime}-\omega_2\right)
\end{aligned}
\)
\(
\text { or, } \quad-\frac{I_1}{r_1}\left(\omega_1^{\prime}-\omega_1\right)=\frac{I_2}{r_2}\left(\omega_2^{\prime}-\omega_2\right) . \quad \ldots \text { (ii) }
\)
Solving (i) and (ii),
\(
\omega_1^{\prime}=\frac{I_1 \omega_1 r_2+I_2 \omega_2 r_1}{I_2 r_1^2+I_1 r_2^2} r_2 \text { and } \omega_2^{\prime}=\frac{I_1 \omega_1 r_2+I_2 \omega_2 r_1}{I_2 r_1^2+I_1 r_2^2} r_1 \text {. }
\)

Q26: A cylinder of mass \(m\) is suspended through two strings wrapped around it as shown in Figure (10-W19). Find (a) the tension \(T\) in the string and (b) the speed of the cylinder as it falls through a distance \(h\).

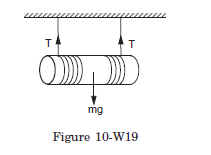
Answer: The portion of the strings between the ceiling and the cylinder is at rest. Hence the points of the cylinder where the strings leave it are at rest. The cylinder is thus rolling without slipping on the strings. Suppose the centre of the cylinder falls with an acceleration \(a\). The angular acceleration of the cylinder about its axis is \(\alpha=a / R\), as the cylinder does not slip over the strings.
The equation of motion for the centre of mass of the cylinder is
\(
m g-2 T=m a \dots(i)
\)
and for the motion about the centre of mass, it is
\(
\begin{aligned}
& 2 \operatorname{Tr}=\left(\frac{1}{2} m r^2 \alpha\right)=\frac{1}{2} m r a \\
& 2 T=\frac{1}{2} m a \dots(ii) \\
&
\end{aligned}
\)
From (i) and (ii),
\(
a=\frac{2}{3} g \text { and } T=\frac{m g}{6} .
\)
As the centre of the cylinder starts moving from rest, the velocity after it has fallen through a distance \(h\) is
given by
\(
\begin{aligned}
& v^2=2\left(\frac{2}{3} g\right) h \\
& v=\sqrt{\frac{4 g h}{3}} \text {. } \\
&
\end{aligned}
\)

Q27: A force \(F\) acts tangentially at the highest point of a sphere of mass \(m\) kept on a rough horizontal plane. If the sphere rolls without slipping, find the acceleration of the centre of the sphere.

Answer: 

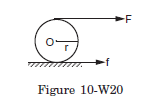
The situation is shown in figure \((10-\mathrm{W} 20)\). As the force \(F\) rotates the sphere, the point of contact has a tendency to slip towards left so that the static friction on the sphere will act towards right. Let \(r\) be the radius of the sphere and \(a\) be the linear acceleration of the centre of the sphere. The angular acceleration about the centre of the sphere is \(\alpha=a / r\), as there is no slipping.
For the linear motion of the centre
\(
F+f=m a \dots(i)
\)
and for the rotational motion about the centre,
\(
F r-f r=I \alpha=\left(\frac{2}{5} m r^2\right)\left(\frac{a}{r}\right)
\)
or,
\(
F-f=\frac{2}{5} m a \dots(ii)
\)
From (i) and (ii),
\(
2 F=\frac{7}{5} m a \text { or, } a=\frac{10 \mathrm{~F}}{7 \mathrm{~m}} .
\)

Q28: A sphere of mass \(M\) and radius \(r\) shown in figure (10-W21) slips on a rough horizontal plane. At some instant, it has translational velocity \(v_0\) and rotational velocity about the centre \(\frac{v_0}{2 r}\). Find the translational velocity after the sphere starts pure rolling.

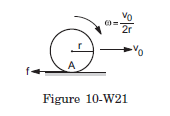
Answer: Let us consider the torque about the initial point of contact \(A\). The force of friction passes through this point and hence its torque is zero. The normal force and the weight balance each other. The net torque about \(A\) is zero. Hence the angular momentum about \(A\) is conserved.
Initial angular momentum is,
\(
\begin{aligned}
L & =L_{c m}+M r v_0=I_{c m} \omega_0+M r v_0 \\
& =\left(\frac{2}{5} M r^2\right)\left(\frac{v_0}{2 r}\right)+M r v_0=\frac{6}{5} M r v_0 .
\end{aligned}
\)
Suppose the translational velocity of the sphere, after it starts rolling, is \(v\). The angular velocity is \(v / r\). The angular momentum about \(A\) is,
\(
\begin{aligned}
L & =L_{c m}+M r v \\
& =\left(\frac{2}{5} M r^2\right)\left(\frac{v}{r}\right)+M r v=\frac{7}{5} M r v .
\end{aligned}
\)
Thus,
\(
\begin{aligned}
\frac{6}{5} M r v_0 & =\frac{7}{5} M r v \\
v & =\frac{6}{7} v_0 .
\end{aligned}
\)

Q29: The sphere shown in figure (10-W22) lies on a rough plane when a particle of mass \(m\) travelling at a speed \(v_0\) collides and sticks with it. If the line of motion of the particle is at a distance \(h\) above the plane, find (a) the linear speed of the combined system just after the collision, (b) the angular speed of the system about the centre of the sphere just after the collision and (c) the value of \(h\) for which the sphere starts pure rolling on the plane. Assume that the mass \(M\) of the sphere is large compared to the mass of the particle so that the centre of mass of the combined system is not appreciably shifted from the centre of the sphere.

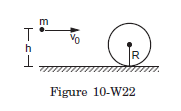
Answer: Take the particle plus the sphere as the system. (a) Using the conservation of linear momentum, the linear speed of the combined system \(v\) is given by
\(
m v_0=(M+m) v \quad \text { or, } \quad v=\frac{m v_0}{M+m} . \quad \ldots \text { (i) }
\)
(b) Next, we shall use the conservation of angular momentum about the centre of mass, which is to be taken at the centre of the sphere \((M \gg m)\). The angular momentum of the particle before the collision is \(m v_0(h-R)\). If the system rotates with angular speed \(\omega\) after the collision, the angular momentum of the system becomes
\(
\left(\frac{2}{5} M R^2+m R^2\right) \omega .
\)
Hence,
\(
\begin{gathered}
m v_0(h-R)=\left(\frac{2}{5} M+m\right) R^2 \omega \\
\omega=\frac{m v_0(h-R)}{\left(\frac{2}{5} M+m\right) R^2} .
\end{gathered}
\)
(c) The sphere will start rolling just after the collision if \(v=\omega R\), i.e., \(\frac{m v_0}{M+m}=\frac{m v_0(h-R)}{\left(\frac{2}{5} M+m\right) R}\)
giving, \(h=\left(\frac{\frac{7}{5} M+2 m}{M+m}\right) R \approx \frac{7}{5} R\).

Short Question Answers

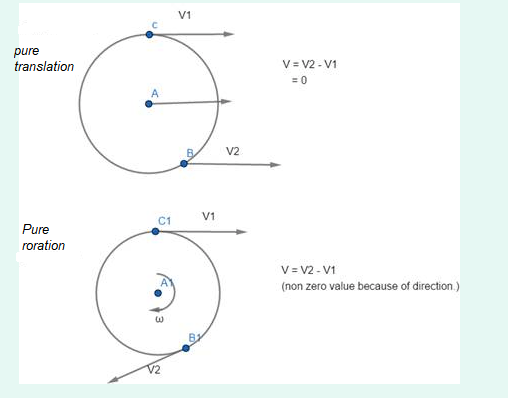
Q1: Can an object be in pure translation as well as in pure rotation?

Answer: The answer to this question is no. To justify we can use the concept of relative motion. In pure translation, the relative velocity between any two random points on an extended body is always zero. But in the case of pure rotation, the relative velocity between any two points on the same circle can never be zero.

Q2: A simple pendulum is a point mass suspended by a light thread from a fixed point. The particle is displaced towards one side and then released. It makes small oscillations. Is the motion of such a simple pendulum a pure rotation? If yes, where is the axis of rotation?

Answer: Yes, this is an example of pure rotation.
The axis of rotation is in the perpendicular direction of the plane of oscillation through the fixed point.

Q3: In a rotating body, \(a=\alpha r\) and \(v=\omega r\). Thus \(\frac{a}{\alpha}=\frac{v}{\omega}\). Can you use the theorems of ratio and proportion studied in algebra so as to write
\(
\frac{a+\alpha}{a-\alpha}=\frac{v+\omega}{v-\omega}
\)

Answer: So, it is meaningless to add or subtract these quantities as they are dimensionally different. This is also applicable for \(v\) and \(\omega\).

Q4: A ball is whirled in a circle by attaching it to a fixed point with a string. Is there an angular rotation of the ball about its centre? If yes, is this angular velocity equal to the angular velocity of the ball about the fixed point?

Answer: Yes, the ball is going to have an angular rotation about its center.
The angular velocities are going to be the same. When the conjunction of the ball and string reaches the initial point, the ball reaches the same point too. Hence, they are moving with the same angular velocities. So, the angular velocity about the center is equal to the angular velocity of the ball about the fixed point.

Explanation:
Let the time period of angular rotation of the ball be \(T\).
Therefore, we get
Angular velocity of the ball about the fixed point \(=\frac{2 \pi}{T}\)
After one revolution about the fixed centre is completed, the ball has come back to its original position. In this case, the point at which the ball meets with the string is again visible after one revolution. This means that it has undertaken one complete rotation about its centre.
The ball has taken one complete rotation about its centre. Therefore, we have
Angular displacement of the ball \(=2 \pi\)
Time period \(=T\)
So, angular velocity is again \(\frac{2 \pi}{T}\).
Thus, in both cases, angular velocities are the same.

Q5: The moon rotates about the earth in such a way that only one hemisphere of the moon faces the earth (figure 10-Q1). Can we ever see the “other face” of the moon from the earth? Can a person on the moon ever see all the faces of the earth?

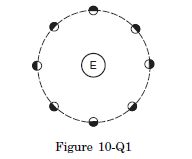
Answer: We will never see the other face of the moon. Because only one hemisphere of the moon is facing the earth.
But all the faces of earth are visible from the moon.
Because the time period of rotation (27 days) and revolution (27.322 days) of the moon are approximately the same. But the earth’s spinning time is around 24 hours. So, the person on the bright side can see all the faces of the earth.

Q6: The torque of the weight of any body about any vertical axis is zero. Is it always correct?

Answer: 

No. To justify this let us see two cases.
Case 1: Torque about a point on the vertical axis.
\(\tau=r F \sin \theta\)
Here \(\theta=\pi\)
\(\tau=r F \sin \pi\)
\(\tau=0\)
Case-2: Torque about an axis at some distance from the path of motion.
\(
\tau=r F \sin \theta
\)
Here \(\theta \in(0,-\pi) \tau \neq 0\)

Q7: \(\underset{\rightarrow}{T}\) he torque of a force \(\underset{\rightarrow}{\rightarrow}\) about a point is defined as \(\vec{\Gamma}=\vec{r} \times \vec{F}\). Suppose \(\vec{r}, \vec{F}\) and \(\vec{\Gamma}\) are all nonzero. Is \(\vec{r} \times \vec{\Gamma} \| \vec{F}\) always true? Is it ever true?

Answer:
No, \(\vec{r} \times \vec{\tau} \| \vec{\Gamma}\) is not true
In fact, it is never true. This is because:
\(
\begin{aligned}
& \vec{r} \times \vec{\tau} \\
& =\vec{r} \times(\vec{r} \times \vec{F})
\end{aligned}
\)
Applying vector triple product, we get:
\(
\begin{aligned}
& \vec{r} \times(\vec{r} \times \vec{F}) \\
& =(\vec{r} \cdot \vec{F}) \vec{r}-(\vec{r} \cdot \vec{r}) \vec{F}
\end{aligned}
\)
\(
\begin{aligned}
& \because \overrightarrow{r \cdot r}=r^2 \\
& =(\vec{r} \cdot \vec{F}) \vec{r}- r^2 \vec{F}
\end{aligned}
\)
\(
\text { If } \vec{r} \cdot \vec{F}=0
\)
\(
\vec{r} \times \vec{\Gamma}={-r^2} \vec{F}
\)
We know that \(r^2\) is never negative and \(\vec{r} \times \vec{\Gamma}=-r^2 \vec{F}\). This implies that both vectors may be antiparallel to each other but not parallel.

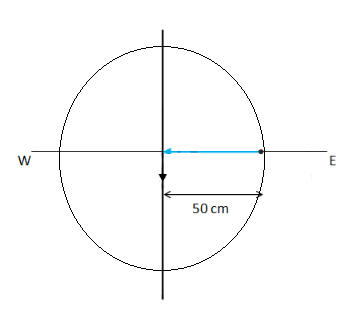
Q8: A heavy particle of mass \(m\) falls freely near the earth’s surface. What is the torque acting on this particle about a point \(50 \mathrm{~cm}\) east to the line of motion? Does this torque produce any angular acceleration in the particle?

Answer: We know that
\(
\vec{\tau}=\vec{r} \times \vec{F}
\)
Given:-
\(
\begin{aligned}
& \vec{r}=-0.5 \hat{i} m \\
& \vec{F}=-m g \hat{j}
\end{aligned}
\)
The torque becomes
\(
\begin{aligned}
& \vec{\tau}=0.5(-\hat{i}) \times m g(-\hat{j}) \\
& \vec{\tau}=0.5 \mathrm{mg} \hat{k}[\because \hat{i} \times \hat{j}=\hat{k}]
\end{aligned}
\)
No, there will be no angular acceleration on the particle due to the torque.
Angular acceleration is given by \(\alpha=\frac{\tau}{I}\). As the particle here moves in a straight line, the centre of rotation lies at a distance infinity \((r=\infty)\); so, the moment of inertia \(\left(I=m r^2\right)\) of the particle is infinity.
\(
\therefore \alpha=0
\)

Q9: If several forces act on a particle, the total torque on the particle may be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces acting on different particles of a body in such a way that their lines of action intersect at a common point?

Answer: Let us assume there are \(\mathrm{n}\) number of forces acting on \(\mathrm{H}\). so, the torque will be
\(
\vec{\tau}=\vec{R} \times \vec{F}_1+\vec{R} \times \vec{F}_2+\vec{R} \times \vec{F}_3+\cdots+\vec{R} \times \vec{F}_n
\)
\(
\vec{\tau}=\vec{R} \times\left(\vec{F}_1+\vec{F}_2+\vec{F}_3+\cdots+\vec{F}_n\right)
\)
\(
\vec{\tau}=\vec{R} \times \vec{F}_{\text {resultant }}
\)
Hence, the statement is proved.
This statement is valid till there exists a common point of intersection.

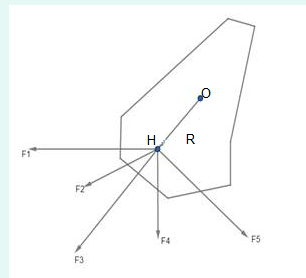
Let us assume there exists \(n\) number of forces having a common point of intersection \(\mathrm{P}\). The forces Are applied at particles A, B, C… We are going to find the torque about the point \(\mathrm{O}\).

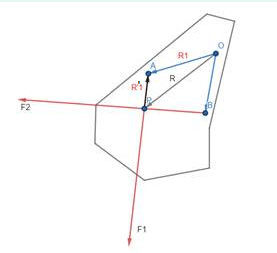
In the diagram A is connected by \(\mathbf{R}_{\mathbf{1}}\). Using vector summation we can write
\(
\vec{R}_1=\vec{R}+\vec{R}_1^{\prime}
\)
So, for the \(i^{\text {th }}\) particle
\(
\vec{R}_i=\vec{R}+\vec{R}^{\prime}{ }_i
\)
Torque,
\(
\vec{\tau}=\vec{R}_1 \times \vec{F}_1+\vec{R}_2 \times \vec{F}_2+\vec{R}_3 \times \vec{F}_3+\cdots+\vec{R}_n \times \vec{F}_n
\)
\(
\vec{\tau}=\left(\vec{R}+\vec{R}_1^{\prime}\right) \times \vec{F}_1+\left(\vec{R}+\vec{R}^{\prime}{ }_2\right) \times \vec{F}_2+\cdots+\left(\vec{R}+\vec{R}^{\prime}{ }_n\right) \times \vec{F}_n
\)
But
\(
\sum_{i=1}^n \overrightarrow{\boldsymbol{R}}_i^{\prime} \times \overrightarrow{\boldsymbol{F}}_i=0
\)
as the angle between them is \(\pi\).
So,
\(
\vec{\tau}=\vec{R} \times \vec{F}_1+\vec{R} \times \vec{F}_2+\vec{R} \times \vec{F}_3+\cdots+\vec{R} \times \vec{F}_n
\)
\(
\vec{\tau}=\vec{R} \times\left(\vec{F}_1+\vec{F}_2+\vec{F}_3+\cdots+\vec{F}_n\right)
\)
\(
\vec{\tau}=\vec{R} \times \vec{F}_{\text {resultant }}
\)
Hence, the statement is valid till it has a common point of intersection.

Q10: If the sum of all the forces acting on a body is zero, is it necessarily in equilibrium? If the sum of all the forces on a particle is zero, is it necessarily in equilibrium?

Answer: No, if the sum of all the forces acting on a body is zero, the body is not necessarily in equilibrium. To be in equilibrium, the sum of torque acting on the body must be zero too (see the figure). In the above case, although the sum of the forces acting on the body is zero \(\left(\overrightarrow{F_1}+\left(-\overrightarrow{F_1}\right)=0\right)\). Still, the body will rotate along \(\overrightarrow{O P}\). So, it won’t remain in equilibrium.

Note: In the case of a particle it remains in equilibrium when the resultant force is zero.

Q11: If the angular momentum of a body is found to be zero about a point, is it necessary that it will also be zero about a different point?

Answer: No, it is not.
\(
\vec{L}=\vec{r} \times \vec{P}
\)
So, it always depends upon the point we are calculating from.

Angular momentum is dependent on the position vector of the particle, angle between the radius vector and the linear velocity of the particle. So, there may be finite angular momentum along any different point even if it is zero at a particular point.If angular momentum is zero along \(\mathrm{O}^{\prime}\) but finite along \(\mathrm{O}\).

Q12: If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point?

Answer:  No, it is not necessary that the torque about any other point be zero if it is zero about one point.
\(
\vec{\tau}=\vec{r} \times \vec{F}
\)
So, it always depends upon the point we are calculating from.

Q13: A body is in translational equilibrium under the action of coplanar forces. If the torque of these forces is zero about a point, is it necessary that it will also be zero about any other point?

Answer: Here the body is in translational equilibrium. We are assuming \(n\) different forces at \(n\) different particles.

\(
\sum_{i=1}^n \vec{F}_i=0
\)
Let us say the torque about \(\mathrm{R}\) is zero.
\(
\vec{\tau}=\sum_{i=1}^n \vec{P}_i \times \vec{F}_i=0
\)
Now let us find the torque about \(O\) now
\(
\begin{aligned}
& \vec{\tau}=\sum_{i=1}^n \vec{S}_i \times \vec{F}_i \\
& \vec{\tau}=\sum_{i=1}^n\left(\vec{Q}_i+\vec{P}_i\right) \times \vec{F}_i \\
& \vec{\tau}=\sum_{i=1}^n \vec{Q}_i \times \vec{F}_i+\sum_{i=1}^n \vec{P}_i \times \vec{F}_i \\
& \vec{\tau}=\vec{Q}_i \times \sum_{i=1}^n \vec{F}_i
\end{aligned}
\)
\(
\vec{\tau}=0
\)
This proves that the torque about any other point will also be zero.

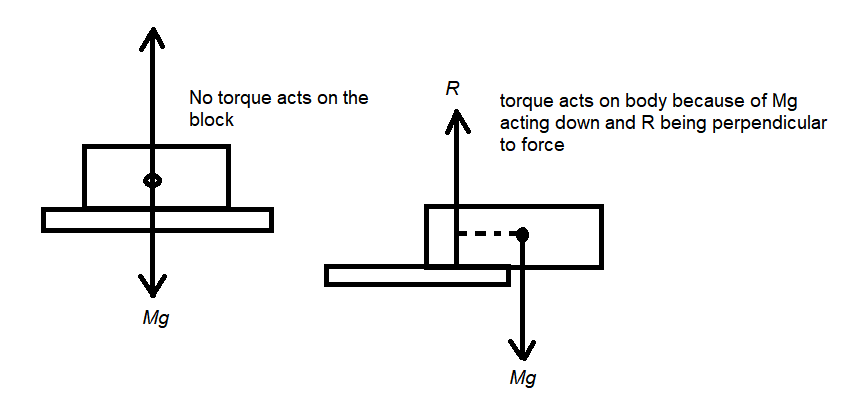
Q14: A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.

Answer: The centre of mass (CM) of a rectangular block lies in the middle of the block. When the block is projected less than half of its length (CM being over the table), no net force acts on it. Thus, no net torque acts upon the body . But if the block is projected more than half of its length outside the table (CM being outside the table), the gravitational force acts along the CM of the block. This force produces a moment along the edge of the table. This rotates the block, and as a result, it falls down.

Q15: When a fat person tries to touch his toes, keeping the legs straight, he generally falls. Explain with reference to figure \((10-\mathrm{Q} 2)\).

Answer: As he starts to bent down the center of mass gets shifted. As soon as it goes beyond his legs, the force exerted by his hands produces a torque around the center of mass. Hence, he falls down.

Q16: A ladder is resting with one end on a vertical wall and the other end on a horizontal floor. Is it more likely to slip when a man stands near the bottom or near the top?

Answer: 

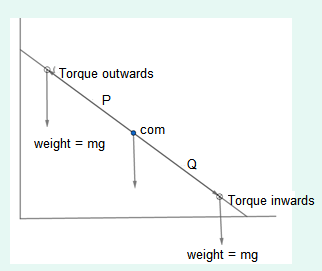
For this, we are going to count the torque about COM.
Now, when the guy stands near the top
\(
\tau=m_{\operatorname{COM}} g \times 0+m g p \sin \theta \text { (outside of plane of paper). }
\)
Hence, he is more likely to slip down.
Now, if he stands near the bottom,
\(\tau=m_{\text {COM }} g \times 0+m g q \sin \theta\) (inside of plane of paper).
So, he will less likely slip down.

Q17: When a body is weighed on an ordinary balance we demand that the arm should be horizontal if the weights on the two pans are equal. Suppose equal weights are put on the two pans, the arm is kept at an angle with the horizontal and released. Is the torque of the two weights about the middle point (point of support) zero? Is the total torque zero? If so, why does the arm rotate and finally become horizontal?

Answer:

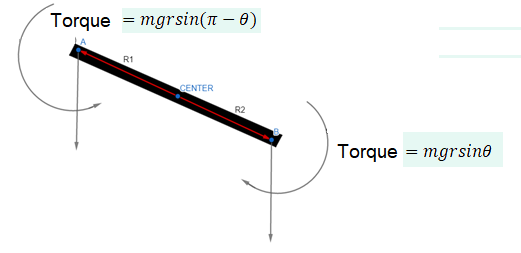
The torque on \(\mathrm{A}\)
\(
\tau=m g r \sin (\pi-\theta)
\)
\(
\tau=m g r \sin \theta
\)
The torque on \(B\)
\(
\tau=m g r \sin \theta
\)
So, the net torque is zero.
But this is all about equilibrium. When the angle was initially constructed, we had to do some work against gravity. When we release the hindrance the system tries to attain its stability back to remain at minimum potential energy. This is why the balance attains its equilibrium again.

Q18: The density of a rod \(A B\) continuously increases from \(A\) to \(B\). Is it easier to set it in rotation by clamping it at \(A\) and applying a perpendicular force at \(B\) or by clamping it at \(B\) and applying the force at \(A\)?

Answer: 

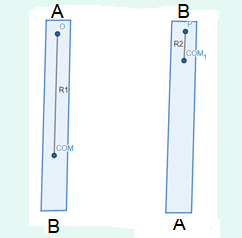
When there is no constraints attached, the whole mass is concentrated at the center of mass of the rod which is more towards \(B\) as the mass concentration is higher.
From the diagram, \(R_1>R_2\)
Now, moment of inertia, \(m R_1{ }^2>m R_2{ }^2\)
\(
m R_1^2 \vec{\alpha}>m R_2^2 \vec{\alpha}
\)
\(
\vec{\tau}_1>\vec{\tau}_2
\)
\(
\vec{F}_1>\vec{F}_2
\)
So, the first one is easier to rotate.

Q19: When tall buildings are constructed on Earth, the duration of day-night slightly increases. Is it true?

Answer: It increases the moment of inertia. Angular momentum \(L=I \omega\). The angular momentum of earth is constant. So the angular velocity decreases. Hence, the duration of the day-night slightly increases.

Q20: If the ice at the poles melts and flows toward the equator, how will it affect the duration of day-night?

Answer: If the ice at the pole melts and flows towards the equator then the radius at that region increases. This increases the moment of inertia. So, the angular velocity also decreases, and the duration of day and night increases.

Q21: A hollow sphere, a solid sphere, a disc, and a ring all having the same mass and radius are rolled down on an inclined plane. If no slipping takes place, which one will take the smallest time to cover a given length?

Answer: Moment of inertia is the rotational analogous of mass.
\(I_{\text {holosphere }}=\left(\frac{2}{3}\right) \mathrm{mr}^2\)
\(I_{\text {solidsphere }}=\left(\frac{2}{5}\right) \mathrm{mr}^2\)
\(I_{\text {disc }}=\left(\frac{1}{2}\right) \mathrm{mr}^2\)
\(I_{\text {ring }}=\mathrm{mr}^2\)
Now, \(\tau=I \alpha\)
So, the one with the least moment of inertia will attain a higher speed. Hence, the solid sphere will take the smallest time.

Q22: A sphere rolls on a horizontal surface. Is there any point of the sphere which has a vertical velocity?

Answer: Some points on the equator of the sphere has got vertical velocity with respect to the direction of motion of the sphere.

Q23: A uniform rod of mass \(m[latex] and length [latex]l\) is struck at an end by a force \(F\) perpendicular to the rod for a short time interval \(t\). Calculate
(a) the speed of the centre of mass, (b) the angular speed of the rod about the centre of mass, (c) the kinetic energy of the rod and (d) the angular momentum of the rod about the centre of mass after the force has stopped to act. Assume that \(t\) is so small that the rod does not appreciably change its direction while the force acts.

Answer: Given
Mass of the rod \(=\mathrm{m}\)
Length of the rod \(=l\)
(a) For the centre of mass,
Acceleration,
\(
a=\frac{F}{m}
\)
Velocity, \(v=a t\)
\(
\Rightarrow v=\frac{F t}{m}
\)
(b) Let the angular speed about the centre of mass be \(\omega\).
Moment of inertia of the rod about centre of mass \(=I=\frac{m l^2}{12}\)
\(
\begin{aligned}
& I \omega=m v r \\
& \Rightarrow \frac{m l^2}{12} \times \omega=m v \frac{l}{2} \\
& \Rightarrow \frac{m l^2}{12} \times \omega=m \times \frac{F t}{m} \times \frac{l}{2} \\
& \Rightarrow \omega=6 \frac{F t}{m l}
\end{aligned}
\)
(c) Kinetic energy,
\(
\begin{aligned}
& \text { K.E. }=\frac{1}{2} m v^2+\frac{1}{2} I \omega^2 \\
& =\frac{1}{2} \times m\left(\frac{F t}{m}\right)^2+\frac{1}{2} \times I \omega^2 \\
& =\frac{1}{2} \times m\left(\frac{F^2 t^2}{m^2}\right)+\frac{1}{2} \times \frac{m l^2}{12} \times\left(\frac{36 F^2 t^2}{m^2 l^2}\right) \\
& =\frac{2 F^2 t^2}{m}
\end{aligned}
\)
(d) Angular momentum about the centre of mass,
\(
\begin{aligned}
& L=m v r \\
& =m \times \frac{F t}{m} \times\left(\frac{l}{2}\right)=\frac{F l t}{2}
\end{aligned}
\)

Q24: Suppose the particle of the previous problem has a mass \(m\) and a speed \(v\) before the collision and it sticks to the rod after the collision. The rod has a mass \(M\). (a) Find the velocity of the centre of mass \(C\) of the system constituting “the rod plus the particle”. (b) Find the velocity of the particle with respect to \(C\) before the collision. (c) Find the velocity of the rod with respect to \(C\) before the collision. (d) Find the angular momentum of the particle and of the rod about the centre of mass \(C\) before the collision. (e) Find the moment of inertia of the system about the vertical axis through the centre of mass \(C\) after the collision. (f) Find the velocity of the centre of mass \(C\) and the angular velocity of the system about the centre of mass after the collision.

Answer: (a) It is given that no external torque and force is applied on the system.
Applying the law of conservation of momentum, we get
\(
\begin{aligned}
& m v=(M+m) v^{\prime} \\
& \Rightarrow v^{\prime}=\frac{m v}{M+m}
\end{aligned}
\)
(b) Velocity of the particle w.r.t. centre of mass (COM) C before the collision \(=v_c=v-v^{\prime}\)
\(
\Rightarrow v_c=v-\frac{m v}{M+m}=\frac{M v}{M+m}
\)
(c) If the body moves towards the rod with a velocity of \(v\), i.e. the rod is moving with a velocity \(-v\) towards the particle.
\(
\text { Therefore the velocity of the rod w.r.t. the centre of mass }=\mathrm{V}^{-}
\)
\(
V^{-}=\frac{M \times 0-m \times v}{M+m}=\frac{-m v}{M+m}
\)
\(
\text { Therefore Velocity of the particle w.r.t. COM C before collision }=-\frac{m v}{M+m}
\)
(d) Distance of the COM from the particle,
\(
\begin{aligned}
& x_{c m}=\frac{m_1 x_1+m_2 x_2}{m_1+m_2} \\
& \Rightarrow r=\frac{M \times \frac{L}{2}+m \times 0}{M+m} \\
& \Rightarrow r=\frac{M L}{2(M+m)}
\end{aligned}
\)
\(\therefore\) Angular momentum of body about COM
\(
\begin{aligned}
& =m v r \\
& =m \times \frac{M v}{(M+m)} \times \frac{M L}{2(M+m)} \\
& =\frac{M^2 m v L}{2(M+m)^2}
\end{aligned}
\)
\(\therefore\) Angular momentum of rod about COM
\(
\begin{aligned}
& =M \times\left(\frac{m v}{(M+m)}\right) \times \frac{1}{2} \frac{m L}{(M+m)} \\
& =\frac{M m^2 v L}{2(M+m)^2}
\end{aligned}
\)
(e) Moment of inertia about COM = \(I\)
\(
\begin{aligned}
& =I_1+I_2 \\
& I=m\left[\frac{M L}{2(M+M)}\right]^2+\frac{M L^2}{12}+M\left[\frac{M L}{2(m+M)}\right]^2 \\
& =\frac{m M^2 L^2}{4(m+M)^2}+\frac{M L^2}{12}+\frac{M m^2 L^2}{4(M+m)^2} \\
& =\frac{3 m M^2 L^2+M(m+M)^2 L^2+3 M m^2 L^2}{12(m+M)^2} \\
& =\frac{M(M+4 m) L^2}{12(M+m)}
\end{aligned}
\)
(f) About COM,
\(
\begin{aligned}
& V_{c m}=\frac{m v}{M+m} \\
& \therefore I \omega=m v r=m v \times \frac{M L}{2(M+m)} \\
& \Rightarrow \omega=\frac{m v M L}{2(M+m)} \times \frac{12(M+m)}{M(M+4 m) L^2} \\
& =\frac{6 m v}{(M+4 m) L}
\end{aligned}
\)

Q25: Two small balls \(A\) and \(B\), each of mass \(m\), are joined rigidly to the ends of a light rod of length \(L\) (figure 10 -E10). The system translates on a frictionless horizontal surface with a velocity \(v_0\) in a direction perpendicular to the rod. A particle \(P\) of mass \(m\) kept at rest on the surface sticks to the ball \(A\) as the ball collides with it. Find
(a) the linear speeds of the balls \(A\) and \(B\) after the collision, (b) the velocity of the centre of mass \(C\) of the system \(A+B+P\) and (c) the angular speed of the system about \(C\) after the collision.

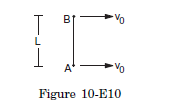
[Hint: The light rod will exert a force on the ball \(B\) only along its length.]

Answer: (a) Collision will not affect the velocity of ball B because the light rod will exert a force on it only along its length.
Therefore, we have
Velocity of \(\mathrm{B}=v_0\)
For ball \(\mathrm{A}\),
On applying the law of conservation of linear momentum, we get
\(
\begin{aligned}
& m v_0=2 m \times v \\
& \Rightarrow v=\frac{v_0}{2}
\end{aligned}
\)
\(\therefore\) Velocity of \(\mathrm{A}=\frac{v_0}{2}\)
(b) If we consider the three bodies to be a system, we have
Net external force \(=0\)
\(
\begin{aligned}
& v_{C M}=\frac{m \times v_0+2 m \times\left(v_0 / 2\right)}{n+2 m} \\
& =\frac{m v_0+m v_0}{3 m} \\
& =\frac{2 v_0}{3}
\end{aligned}
\)
(Direction will be same as the initial velocity before the collision.)
(c) Velocity of \((\mathrm{A}+\mathrm{P})\) w.r.t. the centre of mass \(=\left\{\frac{2 v_0}{3}-\frac{v_0}{2}\right\}=\frac{v_0}{6}\)
Velocity of B w.r.t. the centre of mass \(=v_0-\frac{2 v_0}{3}=\frac{v_0}{3}\)
Distance of the \((\mathrm{A}+\mathrm{P})\) from the centre of mass \(=\frac{l}{3}\)
Distance of the \(B\) from the centre of mass \(=\frac{2 l}{3}\)
Applying \(m v_{\text {com }} r=l_{c m} \times \omega\), we have
\(
\begin{aligned}
& \left(2 m \times \frac{v_o}{6} \times \frac{l}{3}\right)+\left(m \times \frac{v_0}{3} \times \frac{2 l}{3}\right)=\left\{2 m\left(\frac{l}{3}\right)^2+\left(\frac{2 l}{3}\right)^2 m\right\} \times \omega \\
& \Rightarrow \frac{6 m v_0 l}{18}=\frac{6 m l}{9} \omega \\
& \Rightarrow \omega=\frac{v_0}{2 l}
\end{aligned}
\)

Q26: Suppose the rod with the balls \(A\) and \(B\) of the previous problem is clamped at the centre in such a way that it can rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle \(P\) of the same mass \(m\) is dropped from a height \(h\) on the ball \(B\). The particle collides with \(B\) and sticks to it. (a) Find the angular momentum and the angular speed of the system just after the collision. (b) What should be the minimum value of \(h\) so that the system makes a full rotation after the collision?

Answer: (a) Angular momentum \(=m v r\)
Let the particle P collides the ball B with a speed \(u\) and the system moves with speed \(v\) just after the collision.
Applying the law of conservation of linear momentum, we get
\(
\begin{aligned}
m u & =2 m v-m v=m v \\
\therefore u & =v
\end{aligned}
\)
Velocity, \(u=\sqrt{2 g h}\)
and \(r=\frac{L}{2}\)
Initial angular momentum of system about COM of the rod,
\(
\begin{aligned}
& m u r=m \times \sqrt{2 g h} \times \frac{L}{2} \\
& =\frac{m L \sqrt{g h}}{\sqrt{2}}
\end{aligned}
\)
Angular momentum of system about COM of the rod just after the collision \(=l \omega\)
\(
I=\frac{2 m L^2}{4}+\frac{m L^2}{4}=\frac{3 m L^2}{4}
\)
Applying the law of conservation of angular momentum and obtaining the value of \(\omega\), we get
\(
\omega=\frac{m L \frac{\sqrt{g h}}{\sqrt{2}}}{\frac{3 m L^2}{4}}=\frac{\sqrt{8 g h}}{3 L}
\)
(b) When the mass \(2 m\) and \(m\) are at the topmost position and at the lowest point, respectively, they will automatically rotate. In this position, we have
The total gain in potential energy
\(
\begin{aligned}
& =2 m g\left(\frac{L}{2}\right)-m g\left(\frac{L}{2}\right) \\
& \text { Kinetic energy }=\frac{1}{2} I \omega^2
\end{aligned}
\)
Therefore, by the law of conservation of energy, we have
\(
\begin{aligned}
& m g \frac{L}{2}=\frac{1}{2} \times \frac{3}{4} m L^2 \times\left(\frac{8 g h}{9 g L^2}\right) \\
& \Rightarrow h=\frac{3 L}{2}
\end{aligned}
\)

Q27: A hollow sphere is released from the top of an inclined plane of inclination \(\theta\). (a) What should be the minimum coefficient of friction between the sphere and the plane to prevent sliding? (b) Find the kinetic energy of the ball as it moves down a length \(l\) on the incline if the friction coefficient is half the value calculated in part (a).

Answer: 

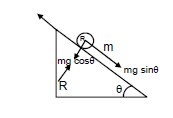
It is given that a hollow sphere is released from the top of an inclined plane of inclination \(\theta\).
(a) To prevent sliding, the body will make only perfect rolling. In this condition, we have
\(
\begin{aligned}
& m g l \sin \theta-f=m a \dots(1) \\
& f \times R=\left(\frac{2}{3}\right) m R^2 \times\left(\frac{a}{R}\right) \\
& \Rightarrow f=\frac{2}{3} m a \dots(2)
\end{aligned}
\)
On putting this value in equation (1), we get
\(
\begin{aligned}
& m g \sin \theta-\frac{2}{3} m a=m a \\
& \Rightarrow a=\frac{3}{5} g \sin \theta
\end{aligned}
\)
From equation (1), we have
\(
\begin{aligned}
& m g \sin \theta-f=\frac{3}{5} m g \sin \theta \\
& \Rightarrow f=\frac{2}{5} m g \sin \theta \\
& \Rightarrow \mu m g \cos \theta=\frac{2}{5} m g \sin \theta \\
& \Rightarrow \mu=\frac{2}{5} \tan \theta
\end{aligned}
\)
(b)
\(
\begin{aligned}
& \left(\frac{1}{5}\right) \tan \theta(m g \cos \theta) R=\frac{2}{3} m R^2 \alpha \\
& \Rightarrow \alpha=\frac{3}{10}\left(\frac{g \sin \theta}{R}\right) \\
& a_c=g \sin \theta-\left(\frac{g}{5}\right) \sin \theta \\
& =\left(\frac{4}{5}\right) g \sin \theta \\
& \Rightarrow t^2=\frac{2 l}{a_c} \\
& =2 l\left(4 g \frac{\sin \theta}{5}\right)\left(\frac{5}{2 g \sin \theta}\right) \\
& \therefore \omega=a t
\end{aligned}
\)
\(
\begin{aligned}
& \text { K.E. }=\frac{1}{2} m \nu^2+\frac{1}{2} I \omega^2 \\
& =\frac{1}{2} m(2 a l)+\frac{1}{2} l\left(a^2 t^2\right) \\
& =\frac{1}{2} m\left(4 g \frac{\sin \theta}{5}\right) \times 2 \times l+\frac{1}{2} \times \frac{2}{3} m R^2 \times \frac{9}{100} \\
& =\left(\frac{\sin ^2 \theta}{R}\right) \times\left(\frac{5 L}{2 g \sin \theta}\right) \\
& =4 m g l \frac{\sin \theta}{5}+3 m g l \frac{\sin \theta}{40} \\
& =\frac{7}{8} m g l \sin \theta
\end{aligned}
\)

Q28: Figure (10-E15) shows a small spherical ball of mass \(m\) rolling down the loop track. The ball is released on the linear portion at a vertical height \(H\) from the lowest point. The circular part shown has a radius \(R\).
(a) Find the kinetic energy of the ball when it is at a point \(A\) where the radius makes an angle \(\theta\) with the horizontal.
(b) Find the radial and the tangential accelerations of the centre when the ball is at \(A\).
(c) Find the normal force and the frictional force acting on the ball if \(H=60 \mathrm{~cm}, R=10 \mathrm{~cm}, \theta=0\) and \(m=70 \mathrm{~g}\).

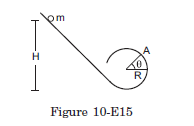
Answer: (a) Let the velocity and angular velocity of the ball at point A be \(v\) and \(\omega\), respectively.
Total kinetic energy at point \(\mathrm{A}=\frac{1}{2} m v^2+\frac{1}{2} I \omega^2\)

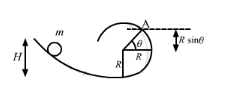
Total potential energy at point \(\mathrm{A}=m g(R+R \sin \theta)\)
In applying the law of conservation of energy, we have
Total energy at initial point = Total energy at A
Therefore, we get
\(
\begin{aligned}
& m g H=\frac{1}{2} m v^2+\frac{1}{2} I \omega^2+m g R(1+\sin \theta) \\
& \Rightarrow m g H-m g R(1+\sin \theta)=\frac{1}{2} m \nu^2+\frac{1}{2} I \omega^2 \\
& \Rightarrow \frac{1}{2} m v^2+\frac{1}{2} I \omega^2=m g(H-R-R \sin \theta) \ldots(1)
\end{aligned}
\)
Total K.E. at \(A=m g(H-R-R \sin \theta)\)
(b) Let us now find the acceleration components.
Putting \(I=\frac{2}{5} m R^2\) and \(\omega=\frac{v}{R}\) in equation (1), we get
\(
\begin{aligned}
& \frac{7}{10} m v^2=m g(H-R-R \sin \theta) \\
& \Rightarrow v^2=\frac{10}{7} g(H-R-R \sin \theta) \dots(2)
\end{aligned}
\)
Radial acceleration,
\(
a_r=\frac{v^2}{R}=\frac{10}{7} \frac{g(H-R-R \sin \theta)}{R}
\)
For tangential acceleration,
Differentiating equation (2) w.r.t. \(t\),
\(
\begin{aligned}
& 2 v \frac{d v}{d t}=-\left(\frac{10}{7}\right) g R \cos \theta \frac{d \theta}{d t} \\
& \Rightarrow \omega R \frac{d v}{d t}=-\left(\frac{5}{7}\right) g R \cos \theta \frac{d \theta}{d t} \\
& \Rightarrow \frac{d v}{d t}=-\left(\frac{5}{7}\right) g \cos \theta \\
& \Rightarrow a_t=-\left(\frac{5}{7}\right) g \cos \theta
\end{aligned}
\)

(c) At \(\theta=0\), from the free body diagram, we have
Normal force \(=N=m a_r\)
\(
\begin{aligned}
& N=m \times \frac{10}{7} \frac{g(H-R-R \sin \theta)}{R} \\
& =\left(\frac{70}{1000}\right) \times\left(\frac{10}{7}\right) \times 10\left\{\frac{0.6-0.1}{0.1}\right\} \\
& =5 N
\end{aligned}
\)
At \(\theta=0\), from the free body diagram, we get
\(
\begin{aligned}
& f_r=m g-m a_t \ldots \ldots \ldots\left(f_r=\text { Force of friction }\right) \\
& \Rightarrow f_r=m\left(g-a_t\right) \\
& =m\left(10-\frac{5}{7} \times 10\right) \\
& =0.07\left(9.8-\frac{5}{7} \times 10\right) \\
& =\frac{1}{100}(70-50)=0.2 N
\end{aligned}
\)