Let us consider the motion of the crest of the wave as shown in Fig. 15.8 which shows the shape of the wave at two instants of time, which differ by a small time interval \(\Delta t\). The entire wave pattern is seen to shift to the right (positive direction of \(x\)-axis) by a distance \(\Delta x\). In particular, the crest shown by a dot \((\bullet)\) moves a \(\text { distance } \Delta x \text { in time } \Delta t \text {. }\)

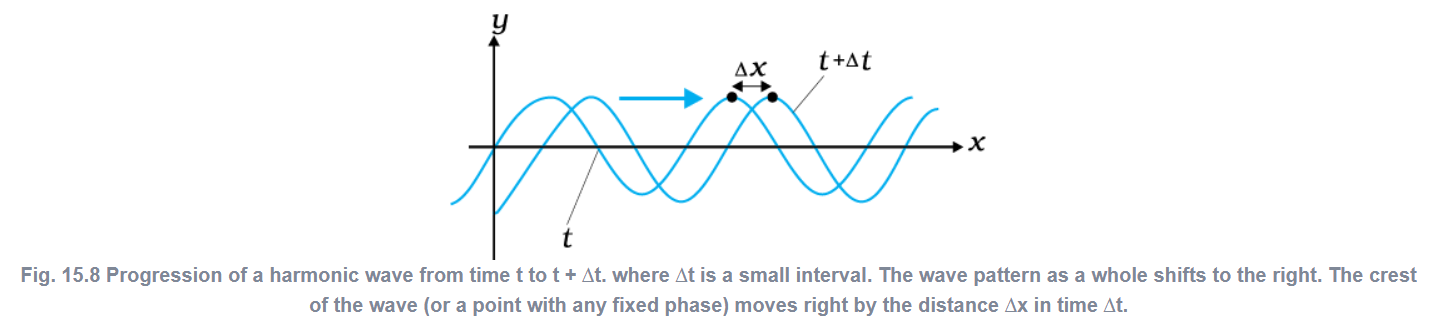
The speed or velocity of the wave is then \(v=\Delta x / \Delta t\).
We can put the \(\operatorname{dot}(\bullet)\) on a point with any other phase. It will move with the same speed \(v\) (otherwise the wave pattern will not remain fixed). That is the waveform will retain its displacement hence the phase of the travelling wave must be constant. The motion of a fixed phase point on the wave is given by
\(
k x-\omega t=\text { constant } \dots(15.10)
\)
Thus, as time \(t\) changes, the position \(x\) of the fixed phase point must change so that the phase remains constant. Thus,
\(
k x-\omega t=k(x+\Delta x)-\omega(t+\Delta t)
\)
or \(k \Delta x-\omega \Delta t=0\)
Taking \(\Delta x, \Delta t\) vanishingly small, this gives
\(
\frac{d x}{\mathrm{~d} t}=\frac{\omega}{k}=v \dots(15.11)
\)
Relating \(\omega\) to \(T\) and \(k\) to \(\lambda\), we get
\(
v=\frac{2 \pi f}{2 \pi / \lambda}=\lambda f=\frac{\lambda}{T} \dots(15.12)
\)

This equation represents the wave velocity of a travelling wave. Eq. (15.12), a general relation for all progressive waves, shows that in the time required for one full oscillation by any constituent of the medium, the wave pattern travels a distance equal to the wavelength of the wave. Travelling waves are also known as progressive waves.

Types of Travelling Waves

There are two types of travelling waves namely, transverse waves and longitudinal waves.

1. Transverse wave: The kind of travelling wave in which the particles oscillate perpendicular to the direction of propagation of the wave. For example, Electromagnetic waves, waves in a string, etc.
2. Longitudinal wave: The kind of travelling wave in which the particles oscillate along the direction of propagation of the wave. For example, Sound waves, heat waves, etc.

Speed of a Transverse Wave on Stretched String

The velocity of a wave travelling on a string depends on the elastic and the inertia properties of the string. When a part of the string gets disturbed, it exerts an extra force on the neighbouring part because of the elastic property. The neighbouring part responds to this force and the response depends on the inertia property. The elastic force in the string is measured by its tension \(F\) and the inertia by its mass per unit length. We have used the symbol \(F\) for tension and not \(T\) in order to avoid confusion with the time period.

Suppose a wave \(y=f\left(t-\frac{x}{v}\right)\) is travelling on the string in the positive \(x\)-direction with a speed \(v\). Let us choose an observer who is riding on a car that moves along the \(x\)-direction with the same velocity \(v\) (figure below). Looking from this frame, the pattern of the string is at rest but the entire string is moving towards the negative \(x\)-direction with a speed \(v\). If a crest is opposite to the observer at any instant, it will always remain opposite to him with the same shape while the string will pass through this crest in an opposite direction like a snake.

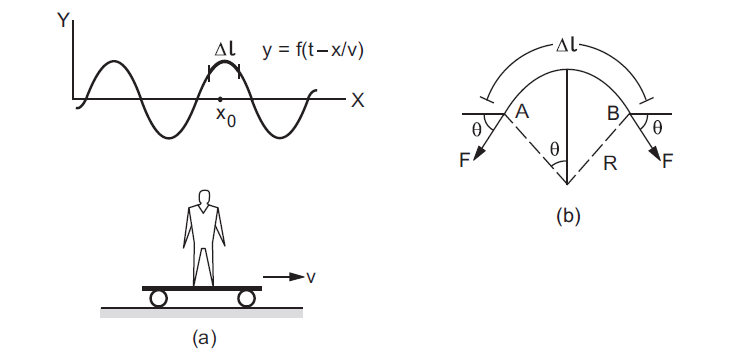
Consider a small element \(A B\) of the string of length \(\Delta l\) at the highest point of a crest. Any small curve may be approximated by a circular arc. Suppose the small element \(\Delta l\) forms an arc of radius \(R\). The particles of the string in this element go in this circle with a speed \(v\) as the string slides through this part. The general situation is shown in Figure (a) and the expanded view of the part near \(\Delta l\) is shown in Figure (b).

We assume that the displacements are small so that the tension in the string does not appreciably change because of the disturbance. The element \(A B\) is pulled by the parts of the string to its right and to its left. The resultant force on this element is in the downward direction as shown in Figure (b) and its magnitude is

\(
F_r=F \sin \theta+F \sin \theta=2 F \sin \theta .
\)
As \(\Delta l\) is taken small, \(\theta\) will be small and
\(
\sin \theta \approx \frac{\Delta l / 2}{R}
\)
so that the resultant force on \(\Delta l\) is
\(
F_r=2 F\left(\frac{\Delta l / 2}{R}\right)=F \Delta l / R .
\)
If \(\mu\) be the mass per unit length of the string, the element \(A B\) has a mass \(\Delta m=\Delta l \mu\). Its downward acceleration is
\(
a=\frac{F_r}{\Delta m}=\frac{F \Delta l / R}{\mu \Delta l}=\frac{F}{\mu R} \dots(15.13)
\)
But the element is moving in a circle of radius \(R\) with a constant speed \(v\). Its acceleration is, therefore, \(a=\frac{v^2}{R}\). The above equation becomes
\(
\begin{aligned}
\frac{v^2}{R} & =\frac{F}{\mu R} \\
v & =\sqrt{F / \mu} .
\end{aligned}
\)
\(
\text { or, } \quad v=\sqrt{F / \mu} \text {. } \dots(15.14)
\)
The velocity of the wave on a string thus depends only on the tension \(F\) and the linear mass density \(\mu\). We have used the approximation that the tension \(F\) remains almost unchanged as the part of the string vibrates up and down. This approximation is valid only for small amplitudes because as the string vibrates, the lengths of its parts change during the course of vibration and hence, the tension changes.

Given the speed of the wave in the medium and the frequency then fixes the wavelength
\(
\lambda=\frac{v}{f} \dots(15.15)
\)

Example 1: \(\mathrm{~A}\) steel wire \(0.72 \mathrm{~m}\) long has a mass of \(5.0 \times 10^{-3} \mathrm{~kg}\). If the wire is under a tension of \(60 \mathrm{~N}\), what is the speed of transverse waves on the wire?

Solution:
Mass per unit length of the wire,
\(
\begin{aligned}
\mu & =\frac{5.0 \times 10^{-3} \mathrm{~kg}}{0.72 \mathrm{~m}} \\
& =6.9 \times 10^{-3} \mathrm{~kg} \mathrm{~m}^{-1}
\end{aligned}
\)
Tension, \(T=60 \mathrm{~N}\)
The speed of the wave on the wire is given by
\(
v=\sqrt{\frac{T}{\mu}}=\sqrt{\frac{60 \mathrm{~N}}{6.9 \times 10^{-3} \mathrm{~kg} \mathrm{~m}^{-1}}}=93 \mathrm{~m} \mathrm{~s}^{-1}
\)

Example 2: The figure below shows a string of linear mass density \(1 \cdot 0 \mathrm{~g} \mathrm{~cm}^{-1}\) on which a wave pulse is travelling. Find the time taken by the pulse in travelling through a distance of \(50 \mathrm{~cm}\) on the string. Take \(g=10 \mathrm{~m} \mathrm{~s}^{-2}\).

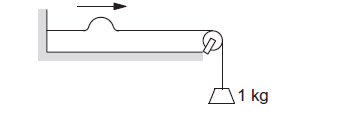
Solution:

The tension in the string is \(F=m g=10 \mathrm{~N}\). The mass per unit length is \(\mu=1 \cdot 0 \mathrm{~g} \mathrm{~cm}^{-1}=0 \cdot 1 \mathrm{~kg} \mathrm{~m}^{-1}\). The wave velocity is, therefore, \(v=\sqrt{F / \mu}=\sqrt{\frac{10 \mathrm{~N}}{0 \cdot 1 \mathrm{~kg} \mathrm{~m}^{-1}}}\) \(=10 \mathrm{~m} \mathrm{~s}^{-1}\). The time taken by the pulse in travelling through \(50 \mathrm{~cm}\) is, therefore, \(0.05 \mathrm{~s}\).

Speed of a Longitudinal Wave (Speed of Sound)

The waves in which the direction of propagation of the wave is along the oscillation of particles are known as longitudinal waves. 

In a longitudinal wave, the constituents of the medium oscillate forward and backward in the direction of propagation of the wave. We have already seen that the sound waves travel in the form of compressions and rarefactions of small-volume elements of air. The elastic property that determines the stress under compressional strain is the bulk modulus of the medium defined by
\(
B=-\frac{\Delta P}{\Delta V / V} \dots(15.16)
\)
Here, the change in pressure \(\Delta P\) produces a volumetric strain \(\frac{\Delta V}{V}\). \(B\) has the same dimension as pressure and given in SI units in terms of pascal \((\mathrm{Pa})\). The inertial property relevant for the propagation of wave is the mass density \(\rho\), with dimensions \(\left[\mathrm{ML}^{-3}\right]\). Simple inspection reveals that quantity \(B / \rho\) has the relevant dimension:
\(
\frac{\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]}{\left[\mathrm{ML}^{-3}\right]}=\left[\begin{array}{ll}
\mathrm{L}^2 & \mathrm{~T}^{-2}
\end{array}\right]
 \dots(15.17)\)
Thus, if \(B\) and \(\rho\) are considered to be the only relevant physical quantities,
\(
v=C \sqrt{\frac{B}{\rho}} \dots(15.18)
\)
where, as before, \(C\) is the undetermined constant from dimensional analysis. The exact derivation shows that \(C=1\). Thus, the general formula for longitudinal waves in a medium is:
\(
v=\sqrt{\frac{B}{\rho}} \dots(15.19)
\)
For a linear medium, like a solid bar, the lateral expansion of the bar is negligible and we may consider it to be only under longitudinal strain. In that case, the relevant modulus of elasticity is Young’s modulus\(Y\), which has the same dimension as the Bulk modulus \(B\).
Thus, the speed of longitudinal waves in a solid bar is given by
\(
v=\sqrt{\frac{Y}{\rho}} \dots(15.20)
\)
where \(Y\) is the Young’s modulus of the material of the bar.
Table 15.1 gives the speed of sound in some media.

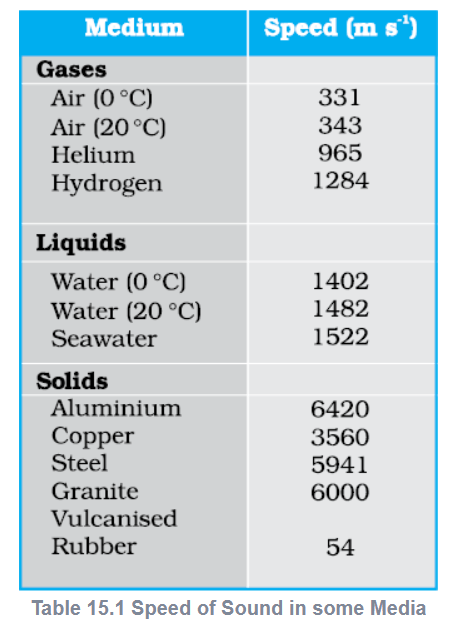
Liquids and solids generally have higher speed of sound than gases. [Note for solids, the speed being referred to is the speed of longitudinal waves in the solid]. This happens because they are much more difficult to compress than gases and so have much higher values of bulk modulus. Now, see Eq. (15.19). Solids and liquids have higher mass densities \((\rho)\) than gases. But the corresponding increase in both the modulus \((B)\) of solids and liquids is much higher. This is the reason why the sound waves travel faster in solids and liquids.

We can estimate the speed of sound in a gas in the ideal gas approximation. For an ideal gas, the pressure \(P\), volume \(V\) and temperature T are related by
\(
\mathrm{PV}=N k_B T \dots(15.21)
\)
where \(N\) is the number of molecules in volume \(V, k_B\) is the Boltzmann constant and \(T\) the temperature of the gas (in Kelvin). Therefore, for an isothermal change, it follows from Eq.(15.21) that
\(
V \Delta P+P \Delta V=0
\)
or \(\quad-\frac{\Delta P}{\Delta V / V}=P\)
Hence, substituting in Eq. (15.16), we have
\(
B=P
\)
Therefore, from Eq. (15.19) the speed of a longitudinal wave in an ideal gas is given by,
\(
v=\sqrt{\frac{P}{\rho}} \dots(15.22)
\)
This relation was first given by Newton and is known as Newton’s formula.

Example 3: Estimate the speed of sound in air at standard temperature and pressure. The mass of 1 mole of air is \(29.0 \times 10^{-3} \mathrm{~kg}\).

Solution:  We know that 1 mole of any gas occupies 22.4 litres at STP. Therefore, the density of air at STP is:
\(\rho_o=\) (mass of one mole of air) / (volume of one mole of air at STP)
\(
\begin{aligned}
& =\frac{29.0 \times 10^{-3} \mathrm{~kg}}{22.4 \times 10^{-3} \mathrm{~m}^3} \\
& =1.29 \mathrm{~kg} \mathrm{~m} \mathrm{~m}^{-3}
\end{aligned}
\)
According to Newton’s formula for the speed of sound in a medium, we get for the speed of sound in air at STP,
\(
v=\left[\frac{1.01 \times 10^5 \mathrm{~N} \mathrm{~m}^{-2}}{1.29 \mathrm{~kg} \mathrm{~m}^{-3}}\right]^{1 / 2}=280 \mathrm{~m} \mathrm{~s}^{-1} \dots(15.23)
\)
The result shown in Eq. (15.23) is about \(15 \%\) smaller as compared to the experimental value of \(331 \mathrm{~m} \mathrm{~s}^{-1}\) as given in Table 15.1. Where did we go wrong? If we examine the basic assumption made by Newton that the pressure variations in a medium during the propagation of sound are isothermal, we find that this is not correct. It was pointed out by Laplace that the pressure variations in the propagation of sound waves are so fast that there is little time for the heat flow to maintain a constant temperature. These variations, therefore, are adiabatic and not isothermal. 

Laplace’s Correction

Newton assumed that the pressure-volume changes in a gas are according to the isothermal process. But according to Laplace, pressure-volume changes occur according to the adiabatic process, and subsequently, an agreement between theoretical and practical observations were made, which favoured Laplace’s observations.

For an adiabatic process, the pressure and volume can change according to the equation:
\(\begin{array}{ll} & P V^\gamma=\text { constant } \\ \text { i.e. } & \Delta\left(P V^\gamma\right)=0 \\ \text { or } & P \gamma V^{\gamma-1} \Delta V+V^\gamma \Delta P=0\end{array}\)
where \(\gamma\) is the ratio of two specific heats, \(\mathrm{C}_{\mathrm{p}} / \mathrm{C}_{\mathrm{v}}\)

Thus, for an ideal gas, the adiabatic bulk modulus is given by,
\(
\begin{aligned}
B_{a d} & =-\frac{\Delta P}{\Delta V / V} \\
& =\gamma P
\end{aligned}
\)
The speed of sound is, therefore, from Eq. (15.19), given by
\(
v=\sqrt{\frac{\gamma P}{\rho}} \dots(15.24)
\)
This modification of Newton’s formula is referred to as the Laplace correction. For air \(\gamma=7 / 5\). Now using Eq. (15.24) to estimate the speed of sound in air at STP, we get a value \(331.3 \mathrm{~m} \mathrm{~s}^{-1}\), which agrees with the measured speed.

Example 4: The ratio of bulk modulus for two liquid mediums is \(4: 1\) and the ratio of its density is \(1: 4\) What will be the ratio of the speed of sound waves for both the mediums?

Solution: Ratio of bulk modulus for two liquid media \(\left(B_1: B_2\right)=4\) :
Ratio of their density \(\left(\rho_1: \rho_2\right)=1,: 4\)
The speed of longitudinal waves in a liquid medium will be given by:
\(v=\sqrt{\frac{B}{\rho}}\)
Hence, we can find the ratio of velocity in sound waves in both mediums as:
\(
\frac{v_1}{v_2}=\sqrt{\frac{B_1 \rho_2}{B_2 \rho_1}}
\)
Substituting the values,
\(
\begin{aligned}
& \frac{v_1}{v_2}=\sqrt{\frac{4}{1} \times \frac{1}{4}} \\
& \therefore v_1: v_2=1: 1
\end{aligned}
\)
The ratio of sound waves in both the given liquid mediums is \(1: 1\)

Power Transmitted Along the String By a Sine Wave

When a travelling wave is established on a string, energy is transmitted along the direction of propagation of the wave. Consider again a sine wave travelling along a stretched string in \(x\)-direction. The equation for the displacement in \(y\)-direction is

\(
y=A \sin \omega(t-x / v) \dots(i)
\)
The figure above shows a portion of the string at a time \(t\) to the right of position \(x\). The string on the left of the point \(x\) exerts a force \(F\) on this part. The direction of this force is along the tangent to the string at position \(x\). The component of the force along the \(Y\)-axis is
\(
F_y=-F \sin \theta \approx-F \tan \theta=-F \frac{\partial y}{\partial x} .
\)
The power delivered by the force \(F\) to the string on the right of position \(x\) is, therefore,
\(
P=\left(-F \frac{\partial y}{\partial x}\right) \frac{\partial y}{\partial t}
\)
By (i), it is
\(
\begin{aligned}
& -F\left[\left(-\frac{\omega}{v}\right) A \cos \omega(t-x / v)\right][\omega A \cos \omega(t-x / v)] \\
& =\frac{\omega^2 A^2 F}{v} \cos ^2 \omega(t-x / v) \text {. } \\
&
\end{aligned}
\)
This is the rate at which energy is being transmitted from left to right across the point at \(x\). The \(\cos ^2\) term oscillates between 0 and 1 during a cycle and its average value is \(1 / 2\). The average power transmitted across any point is, therefore,
\(
P_{a v}=\frac{1}{2} \frac{\omega^2 A^2 F}{v}=2 \pi^2 \mu v A^2 v^2 
\)
The power transmitted along the string is proportional to the square of the amplitude and the square of the frequency of the wave.

Example 5: The average power transmitted through a given point on a string supporting a sine wave is \(0.20 \mathrm{~W}\) when the amplitude of the wave is \(2.0 \mathrm{~mm}\). What power will be transmitted through this point if the amplitude is increased to \(3.0 \mathrm{~mm}\).

Solution:

Other things remaining the same, the power transmitted is proportional to the square of the amplitude.
Thus,
\(
\frac{P_2}{P_1}=\frac{A_2^2}{A_1^2}
\)
or,
\(
\frac{P_2}{0 \cdot 20 \mathrm{~W}}=\frac{9}{4}=2 \cdot 25
\)
or,
\(
P_2=2.25 \times 0.20 \mathrm{~W}=0.45 \mathrm{~W}
\)

Example 6: The equation of a wave travelling on a string stretched along the \(X\)-axis is given by
\(
y=A e^{-\left(\frac{x}{a}+\frac{t}{T}\right)^2} .
\)
(a) Write the dimensions of \(A, a\), and \(T\). (b) Find the wave speed. (c) In which direction is the wave travelling? (d) Where is the maximum of the pulse located at \(t=T\)? At \(t=2 T\)?

Solution:

Given,
Equation of the wave travelling on a string stretched along the \(x\)-axis:
\(
y=A e^{-\left(\frac{x}{a}+\frac{t}{T}\right)^2} 
\)
(a) The dimensions of \(A\) (amplitude), \(T\) (time period) and \(a=\frac{\lambda}{2 \pi}\), which will have the dimensions of the wavelength, are as follows:
\(
\begin{aligned}
& {[A]=\left[M^0 L^1 T^0\right]} \\
& {[T]=\left[M^0 L^0 T^{-1}\right]} \\
& {[a]=\left[M^0 L^1 T^0\right]}
\end{aligned}
\)
\(
\text { (b) Wave speed, } v=\frac{\lambda}{T}=\frac{a}{T}[\lambda=a]
\)
(c) If \(y=f\left(t+\frac{x}{v}\right)\), then the wave travels in the negative direction; and if \(y=f\left(t-\frac{x}{v}\right)\), then the wave travels in the positive direction.
Thus, we have:
\(
y=A e^{-\left(\frac{x}{a}+\frac{t}{T}\right)^2} 
\)
\(
\begin{aligned}
& =A e^{-\frac{1}{T}\left[t+\left(\frac{x T}{a}\right)\right]^2} \\
& =A e^{-\frac{1}{T}\left[t+\frac{x}{V}\right]} \\
& =A e^{-f\left[t+\frac{x}{V}\right]}
\end{aligned}
\)
Hence, the wave is travelling is the negative direction.
(d) Wave speed, \(v=\frac{a}{t}\), Maximum pulse at \(t=T, =\left(\frac{a}{T}\right) \times T=a\)
(Along the negative \(x\)-axis)
Maximum pulse at \(t=2 T, =\left(\frac{a}{T} \times 2 T\right)=2 a\)
(Along the negative \(x\)-axis)
Therefore, the wave is travelling in the negative \(x\)-direction.

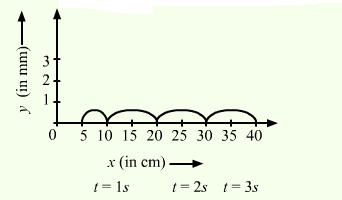
Example 7: The figure below shows a wave pulse at \(t=0\). The pulse moves to the right with a speed of \(10 \mathrm{~cm} \mathrm{~s}^{-1}\). Sketch the shape of the string at \(t=1 \mathrm{~s}, 2 \mathrm{~s}\) and \(3 \mathrm{~s}\).

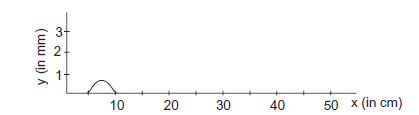
Solution:

Given,
Wave pulse at \(t=0\)

Wave speed \(=10 \mathrm{cms}^{-1}\)
Using the formula \(s=v \times t\), we get:
At :
\(t=1 \mathrm{~s}, s_1=v \times t=10 \times 1=10 \mathrm{~cm}\)
\(t=2 \mathrm{~s}, s_2=v \times t=10 \times 2=20 \mathrm{~cm}\)
\(t=3 \mathrm{~s}, s_3=v \times t=10 \times 3=30 \mathrm{~cm}\)

Example 8: A pulse travelling on a string is represented by the function
\(
y=\frac{a^3}{(x-v t)^2+a^2},
\)
where \(a=5 \mathrm{~mm}\) and \(v=20 \mathrm{~cm} \mathrm{~s}^{-1}\). Sketch the shape of the string at \(t=0,1 \mathrm{~s}\) and \(2 \mathrm{~s}\). Take \(x=0\) in the middle of the string.

Solution:

Function, \(y=\frac{a^3}{(x-v t)^2+a^2}\)
Acceleration, \(a=5 \mathrm{~mm}=0.5 \mathrm{~cm}\)
Velocity, \(v=20 \mathrm{~cms}^{-1}\)
A pulse travelling on a string is represented by the function as,
\(
y=\frac{a^3}{(x-v t)^2+a^2}
\)
At \(t=0 s, y=a^3 /\left(x^2+a^2\right)\)
The graph between \(y\) and \(x\) can be plotted by taking different values of \(x\).
\(
\text { similarly, at } t=1 s, y=a^3 /\left\{(x-v)^2+a^2\right\}
\)
\(
\text { and at } t=2 s, \quad y=a^3 /\left\{(x-2 v)^2+a^2\right\}
\)

Example 9: A wave pulse is travelling on a string with a speed \(v\) towards the positive \(X\)-axis. The shape of the string at \(t=0\) is given by \(g(x)=A \sin (x / a)\), where \(A\) and \(a\) are constants.
(a) What are the dimensions of \(A\) and \(a\)? (b) Write the equation of the wave for a general time \(t\), if the wave speed is \(v\).

Solution:

At \(t=0, g(x)=A \sin (x / a)\)
a) \(\left[\mathrm{M}^0 \mathrm{~L}^1 \mathrm{~T}^0\right]=[\mathrm{A}]\)
\(
[a]=\left[M^0 L^1 T^0\right]=[\mathrm{L}]
\)
b) Wave speed \(=v\)
\(\therefore\) Time period, \(\mathrm{T}=\mathrm{a} / \mathrm{v} (\mathrm{a}=\) wave length \(=\lambda)\)
\(\therefore\) General equation of wave
\(y=A \sin \{(x / a)-t /(a / v)\}\)
\(=A \sin \{(x-v t) / a\}\)

Example 10: The equation of a wave travelling on a string is
\(
y=(0.10 \mathrm{~mm}) \sin \left[\left(31.4 \mathrm{~m}^{-1}\right) x+\left(314 \mathrm{~s}^{-1}\right) t\right] .
\)
(a) In which direction does the wave travel? (b) Find the wave speed, the wavelength, and the frequency of the wave. (c) What is the maximum displacement and the maximum speed of a portion of the string?

Solution:

Given, Equation of the wave,
\(
y=(0.10 \mathrm{~mm}) \sin \left(31.4 \mathrm{~m}^{-1}\right) x+\left(314 \mathrm{~s}^{-1}\right) t
\)
The general equation is \(y=A \sin \left\{\left(\frac{2 \pi x}{\lambda}\right)+\omega t\right\}\)
From the above equation, we can conclude:
(a) The wave is travelling in the negative \(x\)-direction.
\(
\begin{aligned}
& \text { (b) } \frac{2 \pi}{\lambda}=31.4 \mathrm{~m}^{-1} \\
& \Rightarrow \lambda=\frac{2 \pi}{31.4}=0.2 \mathrm{~m}=20 \mathrm{~cm}
\end{aligned}
\)
And,
\(
\begin{aligned}
& \omega=314 s^{-1} \\
& \Rightarrow 2 \pi f=314 \\
& \Rightarrow f=\frac{314}{2 \pi} \\
& =\frac{314}{2 \times 3.14} \\
& =50 s^{-1}=50 \mathrm{~Hz}
\end{aligned}
\)
Wave speed:
\(
\begin{aligned}
& v=\lambda f=20 \times 50 \\
& =1000 \mathrm{~cm} / \mathrm{s}
\end{aligned}
\)
(c) Maximum displacement, \(A=0.10 \mathrm{~mm}\)
Maximum velocity \(=a \omega=0.1 \times 10^{-1} \times 314\) \(=3.14 \mathrm{~cm} / \mathrm{s}\)

Example 11: A wave travels along the positive \(x\)-direction with a speed of \(20 \mathrm{~m} \mathrm{~s}^{-1}\). The amplitude of the wave is \(0.20 \mathrm{~cm}\) and the wavelength \(2.0 \mathrm{~cm}\). (a) Write a suitable wave equation that describes this wave. (b) What is the displacement and velocity of the particle at \(x=2.0 \mathrm{~cm}\) at time \(t=0\) according to the wave equation written? Can you get different values of this quantity if the wave equation is written in a different fashion?

Solution:Wave speed, \(v=20 \mathrm{~m} / \mathrm{s}\)
\(
\begin{aligned}
& A=0.20 \mathrm{~cm} \\
& \lambda=2 \mathrm{~cm}
\end{aligned}
\)
a) Equation of wave along the \(x\)-axis
\(
y=A \sin (k x-w t)
\)
\(
\begin{aligned}
\therefore & \mathrm{k}=2 \pi / \lambda=2 \pi / 2=\pi \mathrm{~cm}^{-1} \\
& \mathrm{~T}=\lambda / \mathrm{v}=2 / 2000=1 / 1000 \mathrm{sec}=10^{-3} \mathrm{sec} \\
& \Rightarrow \omega=2 \pi / \mathrm{T}=2 \pi \times 10^{-3} \mathrm{sec}^{-1}
\end{aligned}
\)
So, the wave equation is,
\(
\therefore \mathrm{y}=(0.2 \mathrm{~cm}) \sin \left[\left(\pi \mathrm{cm}^{-1}\right) \mathrm{x}-\left(2 \pi \times 10^3 \mathrm{sec}^{-1}\right) \mathrm{t}\right]
\)
At \(x=2 \mathrm{~cm}\), and \(t=0\),
\(
\begin{aligned}
& y=(0.2 \mathrm{~cm}) \sin (\pi / 2)=0 \\
& v=r \omega \cos \pi x=0.2 \times 2000 \pi \times \cos 2 \pi=400 \pi
\end{aligned}
\)
\(
\begin{aligned}
& =400 \times(3.14)=1256 \mathrm{~cm} / \mathrm{s} \\
& =400 \pi \mathrm{cm} / \mathrm{s}=4 \pi \mathrm{~m} / \mathrm{s}
\end{aligned}
\)

Example 12: A wave is described by the equation
\(
y=(1 \cdot 0 \mathrm{~mm}) \sin \pi\left(\frac{x}{2 \cdot 0 \mathrm{~cm}}-\frac{t}{0 \cdot 01 \mathrm{~s}}\right) .
\)
(a) Find the time period and the wavelength? (b) Write the equation for the velocity of the particles. Find the speed of the particle at \(x=1.0 \mathrm{~cm}\) at time \(t=0.01 \mathrm{~s}\).
(c) What are the speeds of the particles at \(x=3.0 \mathrm{~cm}\), \(5.0 \mathrm{~cm}\) and \(7.0 \mathrm{~cm}\) at \(t=0.01 \mathrm{~s}\)?
(d) What are the speeds of the particles at \(x=1.0 \mathrm{~cm}\) at \(t=0.011,0.012\), and \(0.013 \mathrm{~s}?\)

Solution:

\(
Y=(1 \mathrm{~mm}) \sin \pi\left[\frac{\mathrm{x}}{2 \mathrm{~cm}}-\frac{\mathrm{t}}{0.01 \mathrm{sec}}\right]
\)
(a)
\(
\begin{aligned}
\mathrm{T} & =2 \times 0.01=0.02 \mathrm{sec}=20 \mathrm{~ms} \\
\lambda & =2 \times 2=4 \mathrm{~cm}
\end{aligned}
\)
(b)
\(
\begin{aligned}
& v=d y / d t=d / d t[\sin 2 \pi(x / 4-t / 0.02)]=-\cos 2 \pi\{x / 4)-(t / 0.02)\} \times 1 /(0.02) \\
& \Rightarrow v=-50 \cos 2 \pi\{(x / 4)-(t / 0.02)\} \\
& \text { at } x=1 \text { and } t=0.01 \mathrm{sec}, v=-50 \cos 2 \pi[(1 / 4)-(1 / 2)]=0
\end{aligned}
\)
(i) at \(x=3 \mathrm{~cm}, \mathrm{t}=0.01 \mathrm{sec}\)
\(
v=-50 \cos 2 \pi(3 / 4-1 / 2)=0
\)
(ii) at \(x=5 \mathrm{~cm}, \mathrm{t}=0.01 \mathrm{sec}, \mathrm{v}=0\) (putting the values)
iii) at \(x=7 \mathrm{~cm}, t=0.01 \mathrm{sec}, v=0\)
at \(x=1 \mathrm{~cm}\) and \(t=0.011 \mathrm{sec}\)
\(
v=-50 \cos 2 \pi\{(1 / 4)-(0.011 / 0.02)\}=-50 \cos (3 \pi / 5)=-9.7 \mathrm{~cm} / \mathrm{sec}
\)
(similarly, the other two can be calculated)

Example 13: A particle on a stretched string supporting a travelling wave, takes \(5.0 \mathrm{~ms}\) to move from its mean position to the extreme position. The distance between two consecutive particles, which are at their mean positions, is \(2.0 \mathrm{~cm}\). Find the frequency, the wavelength and the wave speed.

Solution:

Time period, \(\mathrm{T}=4 \times 5 \mathrm{~ms}=20 \times 10^{-3}=2 \times 10^{-2} \mathrm{~s}\)
\(
\lambda=2 \times 2 \mathrm{~cm}=4 \mathrm{~cm}
\)
\(
\text { frequency, } f=1 / \mathrm{T}=1 /\left(2 \times 10^{-2}\right)=50 \mathrm{~s}^{-1}=50 \mathrm{~Hz}
\)
\(
\text { Wave speed } v=\lambda \mathrm{f}=4 \times 50 \mathrm{~m} / \mathrm{s}=2000 \mathrm{~m} / \mathrm{s}=2 \mathrm{~m} / \mathrm{s}
\)

Example 14: The figure below shows a plot of the transverse displacements of the particles of a string at \(t=0\) through which a travelling wave is passing in the positive \(x\)-direction. The wave speed is \(20 \mathrm{~cm} \mathrm{~s}^{-1}\). Find (a) the amplitude, (b) the wavelength, (c) the wave number and (d) the frequency of the wave.

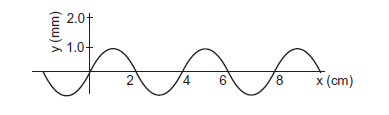
Solution:

Given: Wave speed,
\(
v=20 \mathrm{~cm} / \mathrm{s}
\)
From the graph, we can infer:
(a) Amplitude, \(A=1 \mathrm{~mm}\)
(b) Wavelength, \(\lambda=4 \mathrm{~cm}\)
(c) Wave number,
\(
\begin{aligned}
& k=\frac{2 \pi}{\lambda} \\
& =\frac{(2 \times 3.14)}{4} \\
& =1.57 \mathrm{~cm}^{-2}
\end{aligned}
\)
(d) Time Period, \(T=\frac{\lambda}{v}\)
Frequency, \(\mathrm{f}=\frac{1}{T}=\frac{v}{\lambda}\)
\(
\Rightarrow f=\frac{20}{4}=5 H z
\)

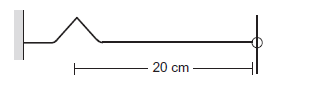
Example 15: A string of linear mass density \(0.5 \mathrm{~g} \mathrm{~cm}^{-1}\) and a total length \(30 \mathrm{~cm}\) is tied to a fixed wall at one end and to a frictionless ring at the other end (figure below). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of \(20 \mathrm{~cm} \mathrm{~s}^{-1}\). The pulse is symmetric about its maximum which is located at a distance of \(20 \mathrm{~cm}\) from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string?

Solution:

The crest reflects as a crest here, as the wire is traveling from a denser to rarer medium. \(\Rightarrow\) phase change \(=0\)
(a) To again original shape distance travelled by the wave \(S=20+20=40 \mathrm{~cm}\).
Wave speed, \(v=20 \mathrm{~m} / \mathrm{s} \Rightarrow\) time \(=\mathrm{s} / \mathrm{v}=40 / 20=2 \mathrm{sec}\)
(b) The wave regains its shape, after traveling a periodic distance \(=2 \times 30=60 \mathrm{~cm}\) \(\therefore\) Time period \(=60 / 20=3 \mathrm{sec}\)
(c) Frequency,
\(
f=\frac{1}{\text { Time period }}=\frac{1}{3} s^{-1}
\)
We know:
\(
f=\frac{1}{2 l} \sqrt{\left(\frac{T}{m}\right)}
\)
Here, \(T\) is the tension in the string.
Now,
\(
\begin{aligned}
& m=\text { Mass per unit length } \\
& =0.5 \mathrm{gm} / \mathrm{cm} \\
& \Rightarrow \frac{1}{3}=\frac{1}{(2 \times 30)} \sqrt{\left(\frac{T}{0.5}\right)} \\
& \Rightarrow T=400 \times 0.5 \\
& =200 \mathrm{dyn} \\
& =2 \times 10^{-3} N
\end{aligned}
\)

Example 16: A travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidally. The amplitude of vibration is \(1.0 \mathrm{~cm}\) and the displacement becomes zero 200 times per second. The linear mass density of the string is \(0.10 \mathrm{~kg} \mathrm{~m}^{-1}\) and it is kept under a tension of \(90 \mathrm{~N}\). (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive \(x\)-direction and at \(t=0\), the end \(x=0\) is at its positive extreme position. Write the wave equation. (c) Find the velocity and acceleration of the particle at \(x=50 \mathrm{~cm}\) at time \(t=10 \mathrm{~ms}\).

Solution:

Given,
Amplitude of the wave \(=1 \mathrm{~cm}\)
Frequency of the wave,
\(f=\frac{200}{2}=100 \mathrm{~Hz}\)
Mass per unit length, \(m=0.1 \mathrm{~kg} / \mathrm{m}\)
Applied tension, \(T=90 \mathrm{~N}\)
(a) Velocity of the wave is given by
\(v=\sqrt{\frac{T}{m}}\)
Thus, we have: \(v=\sqrt{\left(\frac{90}{0.1}\right)}=30 \mathrm{~m} / \mathrm{s}\)
Now, Wavelength, \(\lambda=\frac{v}{f}=\frac{30}{100}=0.3 \mathrm{~m}\)
\(\Rightarrow \lambda=30 \mathrm{~cm}\)
(b) At \(x=0\), displacement is maximum.
Thus, the wave equation is given by
\(
y=(1 \mathrm{~cm}) \cos 2 \pi\left\{\left(\frac{t}{0.01 \mathrm{~s}}\right)-\left(\frac{x}{30 \mathrm{~cm}}\right)\right\} \ldots(1)
\)
(c) Using \(\cos (-\theta)=\cos \theta\)
in equation (1), we get:
\(
y=1 \cos 2 \pi\left(\frac{x}{30}-\frac{t}{0.01}\right)
\)
Velocity, \(v=\frac{d y}{d t}\)
\(
\Rightarrow v=\left(\frac{2 \pi}{0.01}\right)^{d t} \sin 2 \pi\left\{\frac{x}{30}-\frac{t}{0.01}\right\}
\)
And,
Acceleration, \(\quad a=\frac{d v}{d t}\)
\(
\Rightarrow a=\left\{\frac{4 \pi^2}{(0.01)^2}\right\}^{a t} \cos 2 \pi\left\{\left(\frac{x}{30}\right)-\left(\frac{t}{0.01}\right)\right\}
\)
\(
\text { When, } x=50 \mathrm{~cm}, \mathrm{t}=10 \mathrm{~ms}=10 \times 10^{-3} \mathrm{~s}
\)
\(
\begin{aligned}
& v=\left(\frac{2 \pi}{0.01}\right) \sin 2 \pi\left\{\left(\frac{5}{3}\right)-\left(\frac{0.01}{0.01}\right)\right\} \\
& =\left(\frac{2 \pi}{0.01}\right) \sin \left(2 \pi \times \frac{2}{3}\right) \\
& =-\left(\frac{2 \pi}{0.01}\right) \sin \frac{4 \pi}{3} \\
& =-200 \pi \sin \frac{\pi}{3} \\
& =-200 \pi \times \frac{\sqrt{3}}{2} \\
& =-544 \mathrm{~cm} / \mathrm{s} \\
& =-5.4 \mathrm{~m} / \mathrm{s} \\
& \text { In magnitude, } {v}=5.4 \mathrm{~m} / \mathrm{s} .
\end{aligned}
\)
Similarly,
\(
\begin{aligned}
& a=\left\{\frac{4 \pi^2}{(0.01)^2}\right\} \cos 2 \pi\left\{\left(\frac{5}{3}\right)-1\right\} \\
& =4 \pi^2 \times 10^4 \times \frac{1}{2} \\
& \approx 2 \times 10^5 \mathrm{~cm} / \mathrm{s}^2 \text { or } 2 \mathrm{~km} / \mathrm{s}^2
\end{aligned}
\)

Example 17: A heavy but uniform rope of length \(L\) is suspended from a ceiling. (a) Write the velocity of a transverse wave travelling on the string as a function of the distance from the lower end. (b) If the rope is given a sudden sideways jerk at the bottom, how long will it take for the pulse to reach the ceiling? (c) A particle is dropped from the ceiling at the instant the bottom end is given the jerk. Where will the particle meet the pulse?

Solution:

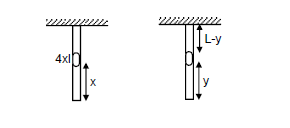
(a) Let \(m\) be the mass per unit length of the string.
Consider an element at a distance \(x\) from the lower end.
Here,
Weight acting downwards \(=(m x) g\)
\(\therefore\) Tension in the string at the upper part \(=m g x\)
The velocity of transverse vibration is given as
\(
\begin{aligned}
& v=\sqrt{\left(\frac{T}{m}\right)}=\sqrt{\left(\frac{m g x}{m}\right)} \\
& \Rightarrow v=\sqrt{(g x)}
\end{aligned}
\)
(b) Let the time taken be \(\mathrm{d} t\) for the small displacement \(\mathrm{d} x\).
Thus, we have:
\(
\begin{aligned}
& d t=\frac{d x}{v}=\frac{d x}{\sqrt{(g x)}} \\
& \therefore \text { Total time, } T=\int_0^L \frac{d x}{\sqrt{(g x)}}=\sqrt{\left(\frac{4 L}{g}\right)}
\end{aligned}
\)
(c) Suppose after time \(t\), the pulse meets the particle at a distance \(y\) from the lower end of the rope.
Now,
\(
\begin{aligned}
t & =\int_0^y \frac{d x}{\sqrt{(g x)}} \\
& =\sqrt{\left(\frac{4 y}{g}\right)}
\end{aligned}
\)
\(\therefore\) Distance travelled by the particle in this time, \(S=L-y\)
Using the equation of motion, we get:
\(
\begin{aligned}
& S=u t+\frac{1}{2} g t^2 \\
& \Rightarrow L-y=\left(\frac{1}{2}\right) g \times\left\{\left(\sqrt{\frac{4 y}{g}}\right)^2\right\} \\
& \Rightarrow L-y=2 y \\
& \Rightarrow 3 y=L \\
& \Rightarrow y=\frac{L}{3}
\end{aligned}
\)
Thus, the particle will meet the pulse at a distance \(\frac{L}{3}\) from the lower end.

Example 18: A tuning fork of frequency \(440 \mathrm{~Hz}\) is attached to a long string of linear mass density \(0.01 \mathrm{~kg} \mathrm{~m}^{-1}\) kept under a tension of \(49 \mathrm{~N}\). The fork produces transverse waves of amplitude \(0.50 \mathrm{~mm}\) on the string. (a) Find the wave speed and the wavelength of the waves. (b) Find the maximum speed and acceleration of a particle of the string. (c) At what average rate is the tuning fork transmitting energy to the string?

Solution:

Given, Frequency of the tuning fork, \(f=440 \mathrm{~Hz}\)
Linear mass density, \(m=0.01 \mathrm{kgm}^{-1}\)
Applied tension, \(T=49 \mathrm{~N}\)
The amplitude of the transverse wave produced by the fork \(=0.50 \mathrm{~mm}\)
Let the wavelength of the wave be \(\lambda\)
(a) The speed of the transverse wave is given by \(v=\sqrt{\left(\frac{T}{m}\right)}\)
\(
\Rightarrow v=\sqrt{\frac{49}{0.01}}=70 \mathrm{~m} / \mathrm{s}
\)
Also,
\(
\begin{aligned}
& v=\frac{f}{\lambda} \\
& \therefore \lambda=\frac{f}{v}=\frac{70}{440}=16 \mathrm{~cm}
\end{aligned}
\)
(b) Maximum speed \(\left(v_{\max }\right)\) and maximum acceleration \(\left(a_{\max }\right)\) :
We have:
\(
\begin{aligned}
& y=A \sin (\omega t-k x) \\
& \therefore v=\frac{d y}{d t}=A \omega \cos (\omega t-k x)
\end{aligned}
\)
Now
\(
\begin{aligned}
& v_{\max }=\left(\frac{d y}{d t}\right)=A \omega \\
& =0.50 \times 10^{-3} \times 2 \pi \times 440 \\
& =1.3816 \mathrm{~m} / \mathrm{s}
\end{aligned}
\)
And,
\(
\begin{aligned}
& a=\frac{d^2 y}{d t^2} \\
& \Rightarrow a=-A \omega^2 \sin (\omega t-k x) \\
& a_{\max }=-A \omega^2 \\
& =0.50 \times 10^{-3} \times 4 \pi^2(440)^2 \\
& =3.8 \mathrm{~km} / \mathrm{s}^2
\end{aligned}
\)
(c) Average rate \((p)\) is given by
\(
\begin{aligned}
& p=2 \pi^2 mv A^2 f^2 \\
& =2 \times 10 \times 0.01 \times 70 \times\left(0.5 \times 10^{-3}\right)^2 \times(440)^2 \\
& =0.67 \mathrm{~W}
\end{aligned}
\)

Example 19: Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than the wavelength divided by \(2 \pi\).

Solution:

Equation of the wave is given by \(y=A \sin (\omega t-k x)\) where
\(A\) is the amplitude
\(\omega\) is the angular frequency
\(k\) is the wave number
Velocity of wave, \(y=A \sin (\omega t-k x)\)
Velocity of particle, \(v_p=\frac{d y}{d t}=A \omega \cos (\omega t-k x)\)
Max velocity of the particle,
\(v_{p_{\max }}=A \omega\)
As given
\(
\begin{aligned}
& A<\frac{\lambda}{2 \pi} \\
& v_{p_{\max }}=\frac{\lambda \omega}{2 \pi} \\
& v_{p_{\max }}<\frac{\omega}{k}\left[\because \frac{2 \pi}{\lambda}=k\right]
\end{aligned}
\)

Example 20: Two wave pulses identical in shape but inverted with respect to each other are produced at the two ends of a stretched string. At an instant when the pulses reach the middle, the string becomes completely straight. What happens to the energy of the two pulses?

Solution:

When two wave pulses identical in shape but inverted with respect to each other meet at any instant, they form a destructive interference. The complete energy of the system at that instant is stored in the form of potential energy within it. After passing each other, both pulses regain their original shape.

Example 21: Show that for a wave travelling on a string
\(
\frac{y_{\max }}{v_{\max }}=\frac{v_{\max }}{a_{\max }}
\)
where the symbols have usual meanings. Can we use componendo and dividendo taught in algebra to write
\(
\frac{y_{\max }+v_{\max }}{y_{\max }-v_{\max }}=\frac{v_{\max }+a_{\max }}{v_{\max }-a_{\max }} ?
\)

Solution:

\(
\begin{aligned}
& \frac{y_{\max }}{v_{\max }}=\frac{v_{\max }}{a_{\max }} \\
& y=A \sin (\omega t-k x) \\
& v=\frac{d y}{d t}=A \cos (\omega t-k x) \\
& v_{\max }=A \omega \\
& a=\frac{d v}{d t}=-A \omega^2 \sin (\omega t-k x) \\
& a_{\max }=\omega^2 A \\
& \text { To prove, } \\
& \frac{y_{\max }}{v_{\max }}=\frac{v_{\max }}{a_{\max }} \\
& L H S \\
& \frac{y_{\max }}{v_{\max }}=\frac{A}{A \omega}=\frac{1}{\omega} \\
& R H S \\
& \frac{v_{\max }}{a_{\max }}=\frac{A \omega}{\omega^2 A}=\frac{1}{\omega}
\end{aligned}
\)
No, componendo and dividendo is not applicable. We cannot add quantities of different dimensions.

Example 22: What is the smallest positive phase constant which is equivalent to \(7 \cdot 5 \pi\)?

Solution:

Equation of the wave: \(y=A \sin (k x-\omega t+\phi)\)
Here, \(A\) is the amplitude, \(k\) is the wave number, \(\omega\) is the angular frequency, and \(\phi\) is the initial phase.
The argument of the sine is a phase, so the smallest positive phase constant should be
\(
\begin{aligned}
& \sin (7.5 \pi)=\sin (3 \times 2 \pi+1.5 \pi) \\
& =\sin (1.5 \pi)
\end{aligned}
\)
Therefore, the smallest positive phase constant is \(1.5 \pi\).

Example 23: A string clamped at both ends vibrates in its fundamental mode. Is there any position (except the ends) on the string which can be touched without disturbing the motion? What if the string vibrates in its first overtone?

Solution:

Yes, at the centre. The centre position is a node. If the string vibrates in its first overtone, then there will be two positions, i.e., two nodes, one at \(x=0\) and the other at \(x=L\).