14.4 Simple harmonic motion and uniform circular motion

In this section, we show that the projection of uniform circular motion on the diameter of the circle follows simple harmonic motion. A simple experiment (Fig. 14.9) helps us visualise this connection. Tie a ball to the end of a string and make it move in a horizontal plane about a fixed point with a constant angular speed. The ball would then perform a uniform circular motion in the horizontal plane. Observe the ball sideways or from the front, fixing your attention in the plane of motion. The ball will appear to execute to and fro motion along a horizontal line with the point of rotation as the midpoint. You could alternatively observe the shadow of the ball on a wall that is perpendicular to the plane of the circle. In this process what we are observing is the motion of the ball on a diameter of the circle normal to the direction of viewing.

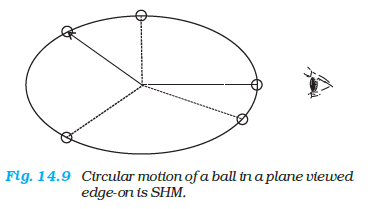
Fig. 14.10 describes the same situation mathematically. Suppose a particle P is moving uniformly on a circle of radius \(A\) with angular speed \(\omega\). The sense of rotation is anticlockwise. The initial position vector of the particle, 1.e., the vector \(\overline{\text { OP }}\) at \(t=0\) makes an angle of \(\phi\) with the positive direction of \(x\)-axis. In time \(t\), it will cover a further angle \(\omega t\) and its position vector will make an angle of \(\omega t+\phi\) with the +ve \(x\)-axis. Next, consider the projection of the position vector OP on the \(x\)-axis. This will be \(\mathrm{OP}^{\prime}\). The position of \(\mathrm{P}^{\prime}\) on the \(x\)-axis, as the particle P moves on the circle, is given by
\(
x(t)=A \cos (\omega t+\phi)
\)

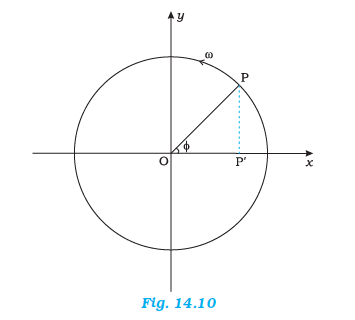
which is the defining equation of SHM. This shows that if P moves uniformly on a circle, its projection \(\mathrm{P}^{\prime}\) on a diameter of the circle executes SHM. The particle P and the circle on which it moves are sometimes referred to as the reference particle and the reference circle, respectively.

We can take projection of the motion of \(P\) on any diameter, say the \(y\)-axis. In that case, the displacement \(y(t)\) of \(\mathrm{P}^{\prime}\) on the \(y\)-axis is given by
\(
y=A \sin (\omega t+\phi)
\)
which is also an SHM of the same amplitude as that of the projection on \(x\)-axis, but differing by a phase of \(\pi / 2\).

Example 1: The figure given below depicts two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution are indicated in the figures. Obtain the simple harmonic motions of the \(x\)-projection of the radius vector of the rotating particle P in each case.

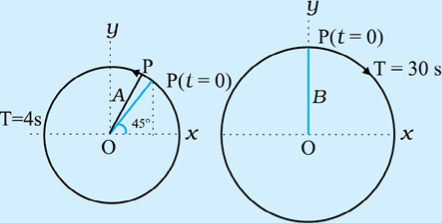
Solution:

(a) At \(t=0\), OP makes an angle of \(45^{\circ}=\pi / 4 \mathrm{rad}\) with the (positive direction of) \(x\)-axis. After time \(t\), it covers an angle \(\frac{2 \pi}{T} t\) in the anticlockwise sense, and makes an angle of \(\frac{2 \pi}{T} t+\frac{\pi}{4}\) with the \(x\)-axis.
The projection of OP on the \(\mathrm{x}\)-axis at time \(t\) is given by,
\(
x(t)=A \cos \left(\frac{2 \pi}{T} t+\frac{\pi}{4}\right)
\)
For \(T=4 \mathrm{~s}\),
\(
x(t)=A \cos \left(\frac{2 \pi}{4} t+\frac{\pi}{4}\right)
\)
which is a SHM of amplitude \(A\), period \(4 \mathrm{~s}\), and an initial phase \(=\frac{\pi}{4}\)

(b) In this case at \(t=0\), OP makes an angle of \(90^{\circ}=\frac{\pi}{2}\) with the \(x\)-axis. After a time \(t\), it covers an angle of \(\frac{2 \pi}{T} t\) in the clockwise sense and makes an angle of \(\left(\frac{\pi}{2}-\frac{2 \pi}{T} t\right)\) with the \(x\)-axis. The projection of OP on the \(x\)-axis at time \(t\) is given by
\(
\begin{aligned}
& x(t)=B \cos \left(\frac{\pi}{2}-\frac{2 \pi}{T} t\right) \\
&=B \sin \left(\frac{2 \pi}{T} t\right)
\end{aligned}
\)
For \(T=30 \mathrm{~s}\),
\(
x(t)=B \sin \left(\frac{\pi}{15} t\right)
\)
Writing this as \(x(t)=B \cos \left(\frac{\pi}{15} t-\frac{\pi}{2}\right)\), and comparing with Eq. (14.4). We find that this represents a SHM of amplitude \(B\), period \(30 \mathrm{~s}\), and an initial phase of \(-\frac{\pi}{2}\).

Example 2: Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial \((t=0)\) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: ( \(x\) is in \(\mathrm{cm}\) and \(t\) is in s).

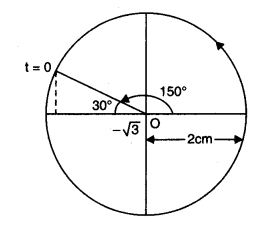
(a) \(x=-2 \sin (3 t+\pi / 3)\)
(b) \(x=\cos (\pi / 6-t)\)
(c) \(x=3 \sin (2 \pi t+\pi / 4)\)
(d) \(x=2 \cos \pi t\)

Solution:

(a) \(x=2 \cos \left(3 t+\frac{\pi}{3}+\frac{\pi}{2}\right)\)
Radius of the reference circle, \(r=\) amplitude of \(\mathrm{SHM}=2 \mathrm{~cm}\),
At
\(
\begin{aligned}
t & =0, \quad x=-2 \sin \frac{\pi}{3}=\frac{-2 \sqrt{3}}{2}=-\sqrt{3} \mathrm{~cm} \\
\omega t & =3 t \quad \therefore \omega=3 \mathrm{rad} / \mathrm{s} \\
\cos \phi_0 & =-\frac{\sqrt{3}}{2}, \quad \phi_0=150^{\circ}
\end{aligned}
\)
The reference circle is, thus, as plotted below.

(b) \(x=\cos \left(t-\frac{\pi}{6}\right)\)
Radius of circle, \(r=\) amplitude of \(\mathrm{SHM}=1 \mathrm{~cm}\).
At
\(
\begin{aligned}
t & =0, \quad x=\cos \frac{\pi}{6}=\frac{\sqrt{3}}{2} \mathrm{~cm} \\
\omega t & =1 t \Rightarrow \omega=1 \mathrm{rad} / \mathrm{s} \\
\cos \phi_0 & =\frac{\sqrt{3}}{2}, \quad \phi_0=-\frac{\pi}{6}
\end{aligned}
\)
The reference circle is, thus as plotted below.

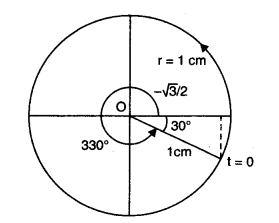
(c) \(x=3 \cos \left(2 \pi t+\frac{\pi}{4}+\frac{\pi}{2}\right)\)
Here, radius of the reference circle, \(r=3 \mathrm{~cm}\) and at \(t=0, x=3 \sin \frac{\pi}{4}=\frac{\sqrt{3}}{2} \mathrm{~cm}\)
\(
\begin{aligned}
\omega t & =2 \pi t \Rightarrow \omega=2 \pi \mathrm{rad} / \mathrm{s} \\
\phi_0 & =\frac{\sqrt{\frac{3}{2}}}{3}=\frac{1}{\sqrt{2}}
\end{aligned}
\)
Therefore, the reference circle is being shown below.

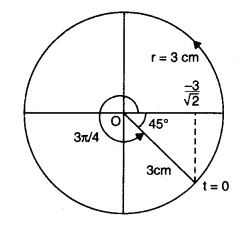
(d)
\(
x=2 \cos \pi t
\)
\(
\text { Radius of reference circle, } r=2 \mathrm{~cm} \text { and at } t=0, x=2 \mathrm{~cm}
\)
\(
\therefore \quad \omega t=\pi t, \text { or } \omega=\pi \mathrm{rad} / \mathrm{s}
\)
\(
\cos \phi_0=1, \phi_0=0
\)
\(
\text { The reference circle is plotted below. }
\)

Example 3: Answer the following questions :

(a) Time period of a particle in SHM depends on the force constant \(k\) and mass \(m\) of the particle:
\(T=2 \pi \sqrt{\frac{m}{k}}\). A simple pendulum executes SHM approximately. Why then is the time period of a pendulum independent of the mass of the pendulum?
(b) The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis
shows that \(T\) is greater than \(2 \pi \sqrt{\frac{l}{g}}\). Think of a qualitative argument to appreciate this result.
(c) A man with a wristwatch on his hand falls from the top of a tower. Does the watch give the correct time during the free fall?
(d) What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity?

Solution:

(a) In the case of a spring, \(\dot{k}\) does not depend upon \(m\). However, in case of a simple pendulum, \(k\) is directly proportional to \(m\) and hence the ratio \(\frac{m}{k}\) is a constant quantity.
(b) The restoring force for the bob of the pendulum is given by
\(
F=-m g \sin \theta
\)
If \(\theta\) is small, then \(\sin \theta=\theta=\frac{y}{l} \quad \therefore \quad F=-\frac{m g}{l} y\)
i.e., the motion is simple harmonic and time period is \(T=2 \pi \sqrt{\frac{l}{g}}\).
Clearly, the above formula is obtained only if we apply the approximation \(\sin \theta \approx \theta\).
For large angles, this approximation is not valid, and \(T\) is greater than \(2 \pi \sqrt{\frac{l}{g}}\).
(c) The wristwatch uses an electronic system or spring system to give the time, which does not change with acceleration due to gravity. Therefore, the watch gives the correct time.
(d) During the free fall of the cabin, the acceleration due to gravity is zero. Therefore, the frequency of oscillations is also zero i.e., the pendulum will not vibrate at all.

Example 4: A cylindrical piece of cork of density of base area \(A\) and height \(h\) floats in a liquid of density \(\rho_l\). The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
\(
T=2 \pi \sqrt{\frac{h \rho}{\rho_l g}}
\)
where \(\rho\) is the density of cork. (Ignore damping due to the viscosity of the liquid).

Solution:

Say, initially in equilibrium, \(y\) height of the cylinder is inside the liquid. Then, the Weight of the cylinder = upthrust due to the liquid displaced
\(\therefore \quad A h \rho g=A y \rho g\)
When the cork cylinder is depressed slightly by \(\Delta y\) and released, a restoring force, equal to additional upthrust, acts on it. The restoring force is
\(
F=A(y+\Delta y) \rho_l g-A y \rho_l g=A \rho_l g \Delta y
\)
\(\therefore \quad\) Acceleration, \(a=\frac{F}{m}=\frac{A \rho_l g \Delta y}{A h \rho}=\frac{\rho_l g}{h \rho} . \Delta y\) and the
acceleration is directed in a direction opposite to \(\Delta y\): Obviously, as \(a \propto-\Delta y\), the motion of cork cylinder is SHM, whose time period is given by
\(
\begin{aligned}
T & =2 \pi \sqrt{\frac{\text { displacement }}{\text { acceleration }}} \\
& =2 \pi \sqrt{\frac{\Delta y}{a}} \\
& =2 \pi \sqrt{\frac{h \rho}{\rho_l g}}
\end{aligned}
\)

Example 5: One end of a U-tube containing mercury is connected to a suction pump and the other end to the atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.

Solution:

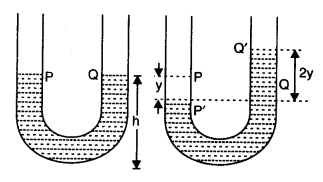
The suction pump creates the pressure difference, thus mercury rises in one limb of the U-tube. When it is removed, a net force acts on the liquid column due to the difference in levels of mercury in the two limbs and hence the liquid column executes S.H.M. which can be expressed as:
Consider the mercury contained in a vertical \(U\)-tube upto the level \(P\) and \(Q\) in its two limbs.
Let \(P=\) density of the mercury.
\(L=\) Total length of the mercury column in both the limbs.
\(A=\) internal cross-sectional area of \(U\)-tube. \(m=\) mass of mercury in \(U\)-tube \(=L A P\).
Assume, the mercury be depressed in the left limb to \(\mathrm{F}\) by a small distance \(y\), then it rises by the same amount in the right limb to position Q’.
\(\therefore\) Difference in levels in the two limbs \(=P^{\prime} Q^{\prime}=2 y\).
\(\therefore\) Volume of mercury contained in the column of length \(2 y=A \times 2 y\)
\(
\therefore \mathrm{m}-\mathrm{A} \times 2 \mathrm{y} \times \rho .
\)
If \(\mathrm{W}=\) weight of liquid contained in the column of length \(2 y\).
Then \(\mathrm{W}=\mathrm{mg}=\mathrm{A} \times 2 \mathrm{y} \times \rho \times g\)
This weight produces the restoring force \((F)\) which tends to bring back the mercury to its equilibrium position.
\(
\therefore \quad F=-2 A y \rho g=-(2 A \rho g) y
\)
If \(\quad a=\) acceleration produced in the liquid column, Then
\(
a=\frac{F}{m}
\)
\(
\begin{aligned}
& =-\frac{(2 A \rho g) y}{L A \rho}=-\frac{2 A \rho g}{L A} \\
& =-\frac{2 \rho g}{2 h \rho} y \dots(i) (\because L=2 h)
\end{aligned}
\)
where \(h=\) height of mercury in each limb. Now from eqn. \((i)\), it is clear that \(a \propto y\) and -ve sign shows that it acts opposite to \(y\), so the motion of mercury in \(u\)-tube is simple harmonic in nature having time period \((T)\) given by
\(
\begin{aligned}
T & =2 \pi \sqrt{\frac{y}{a}}=2 \pi \sqrt{\frac{2 h \rho}{2 \rho g}}=2 \pi \sqrt{\frac{h \rho}{\rho g}} \\
T & =2 \pi \sqrt{\frac{h}{g}}
\end{aligned}
\)

Example 6: An air chamber of volume \(V\) has a neck area of cross section \(a\) into which a ball of mass \(m\) just fits and can move up and down without any friction (Fig. below). Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. below].

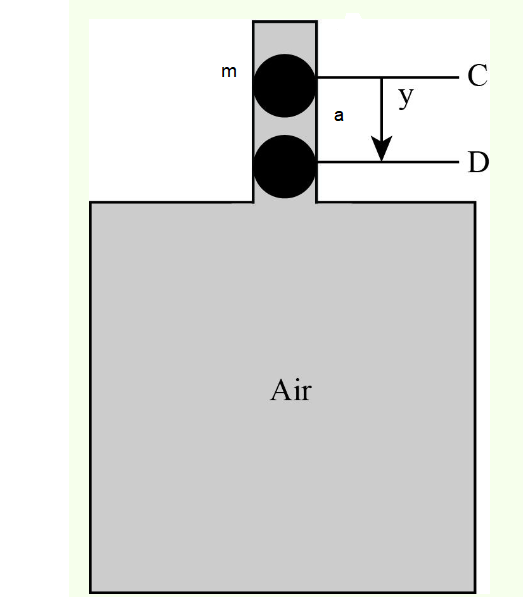
Solution:

Consider an air chamber of volume \(V\) with a long neck of the uniform area of cross-section \(A\), and \(a\) frictionless ball of mass \(\mathrm{m}\) fitted smoothly in the neck at position C, Fig. The pressure of air below the ball inside the chamber is equal to the atmospheric pressure.
Increase the pressure on the ball by a little amount \(p\), so that the ball is depressed to position \(\mathrm{D}\), where \(C D=\) y.
There will be decrease in volume and hence an increase in the pressure of air inside the chamber. The decrease in volume of the air inside the chamber, \(\Delta V=A y\)
\(
\begin{aligned}
\text { Volumetric strain } & =\frac{\text { change in volume }}{\text { original volume }} \\
& =\frac{\Delta \mathrm{V}}{\mathrm{V}}=\frac{A y}{V}
\end{aligned}
\)
\(\therefore\) Bulk Modulus of elasticity \(E\), will be
\(
\begin{aligned}
E & =\frac{\text { stress (or increase in pressure) }}{\text { volumetric strain }} \\
& =\frac{-p}{A y / V}=\frac{-p V}{A y}
\end{aligned}
\)
Here, the negative sign shows that the increase in pressure will decrease the volume of air in the chamber.
Now,
\(
p=\frac{-E A y}{V}
\)
Due to this excess pressure, the restoring force acting on the ball is
\(
F=p \times A=\frac{-E A y}{V} \cdot A=\frac{-E A^2}{V} y \dots(i)
\)
Since \(F \propto y\) and the negative sign shows that the force is directed towards the equilibrium position. If the applied increased pressure is removed from the ball, the ball will start executing linear SHM in the neck of the chamber with \(C\) as the mean position.
In S.H.M., the restoring force,
\(
F=-k y \dots(ii)
\)
Comparing (i) and (ii), we have
\(
\begin{aligned}
& \text { Spring factor, } k=E A^2 / V \\
& \text { inertia factor }=\text { mass of ball }=m \text {. } \\
& \text { Period, } T=2 \pi \sqrt{\frac{\text { inertia factor }}{\text { spring factor }}} \\
& =2 \pi \sqrt{\frac{m}{E A^2 / V}}=\frac{2 \pi}{A} \cdot \sqrt{\frac{m V}{E}} \\
& \therefore \text { Frequency, } f \quad=\frac{1}{T}=\frac{A}{2 \pi} \sqrt{\frac{E}{m V}} \\
&
\end{aligned}
\)

Example 7: In figure below \(k=100 \mathrm{~N} \mathrm{~m}^{-1}, M=1 \mathrm{~kg}\) and \(F=10 \mathrm{~N}\). (a) Find the compression of the spring in the equilibrium position. (b) A sharp blow by some external agent imparts a speed of \(2 \mathrm{~m} \mathrm{~s}^{-1}\) to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant. (c) Find the time period of the resulting simple harmonic motion. (d) Find the amplitude. (e) Write the potential energy of the spring when the block is at the left extreme. (f) Write the potential energy of the spring when the block is at the right extreme.
The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy.

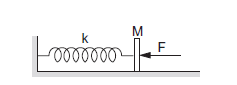
Solution:

It is given that:
Spring constant, \(k=100 \mathrm{~N} / \mathrm{m}\),
Mass of the block, \(M=1 \mathrm{~kg}\)
Force, \(\mathrm{F}=10 \mathrm{~N}\)

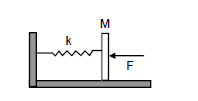
(a) In the equilibrium position,
\(
F=k x
\)
where \(\mathrm{x}\) is the compression of the spring, and \(\mathrm{k}\) is the spring constant.
\(
\begin{aligned}
& \therefore x=\frac{F}{k}=\frac{10}{100} \\
& =0.1 \mathrm{~m}=10 \mathrm{~cm}
\end{aligned}
\)
(b) The blow imparts a speed of 2 ms-1 to the block, towards left. Potential energy of spring, \(\mathrm{U}=\frac{1}{2} k x^2\)
Kinetic energy,
\(
K=\frac{1}{2} M v^2
\)
(c) Time period \((T)\) is given by,
\(
\begin{aligned}
& T=2 \pi \sqrt{\frac{M}{k}} \\
& =2 \pi \sqrt{\frac{1}{100}}=\frac{\pi}{5} s
\end{aligned}
\)
(d) Let \(\mathrm{A}\) be the amplitude.
Amplitude is the distance between the mean and the extreme position.
At the extreme position, compression of the spring will be \((A+x)\).
As the total energy in S.H.M. remains constant, we can write:
\(
\begin{aligned}
& \frac{1}{2} k(A+x)^2=\frac{1}{2} k x^2+\frac{1}{2} M v^2+F x \\
& =2.5+10 x
\end{aligned}
\)
\(
\begin{aligned}
& \therefore 50(\mathrm{~A}+0.1) 2=2.5+10 x \\
& \Rightarrow 50 \mathrm{~A} 2+0.5+10 \mathrm{~A}=2.5+10 \mathrm{~A} \\
& \Rightarrow 50 \mathrm{~A} 2=2 \\
& \Rightarrow A^2=\frac{2}{50}=\frac{4}{100} \\
& \Rightarrow A=\frac{2}{10} m=0.2 m=20 \mathrm{~cm}
\end{aligned}
\)
(e) Potential Energy at the left extreme will be,
\(
\begin{aligned}
& P . E .=\frac{1}{2} k(A+x)^2 \\
& =\frac{1}{2} \times 100 \times(0.1+0.2)^2 \\
& =50 \times(0.09)=4.5 J
\end{aligned}
\)
(f) Potential Energy at the right extreme is calculated as:
Distance between the two extremes \(=2 \mathrm{~A}\)
\(
\begin{aligned}
& P . E .=\frac{1}{2} k(A+x)^2-F(2 A) \\
& =4.5-10(0.4)=0.5 \mathrm{~J}
\end{aligned}
\)
As the work is done by the external force of \(10 \mathrm{~N}\), different values of options (b), (e) and (f) do not violate the law of conservation of energy.

Example 8: Find the time period of the oscillation of mass \(m\) in figures below a,b,c. What is the equivalent spring constant of the pair of springs in each case?

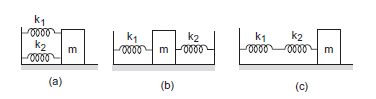
Solution:

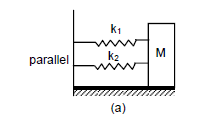
(a) Spring constant of a parallel combination of springs is given as,
\(
K=k_1+k_2 \text { (parallel) }
\)
Using the relation of time period for S.H.M. for the given spring-mass system, we have:
\(
T=2 \pi \sqrt{\frac{m}{K}}=2 \pi \sqrt{\frac{m}{k_1+k_2}}
\)

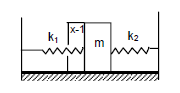
(b) Let \(x\) be the displacement of the block of mass \(m\), towards left.
The resultant force is calculated as,
\(
F=F_1+F_2=\left(k_1+k_2\right) x
\)
Acceleration \((a)\) is given by,
\(
a=\left(\frac{F}{m}\right)=\frac{\left(k_1+k_2\right)}{m} x
\)
Time period \((T)\) is given by ,
\(
T=2 \pi \sqrt{\frac{\text { displacement }}{\text { acceleration }}}
\)
On substituting the values of displacement and acceleration, we get: \(T=2 \pi \sqrt{\frac{x}{x \frac{\left(k_1+k_2\right)}{m}}}\)
\(
=2 \pi \sqrt{\frac{m}{k_1+k_2}}
\)
\(
\text { Required spring constant, } K=k_1+k_2
\)

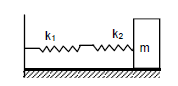
Let \(K\) be the equivalent spring constant of the series combination.
\(
\begin{aligned}
& \frac{1}{K}=\frac{1}{k_1}+\frac{1}{k_2}=\frac{k_2+k_1}{k_1 k_2} \\
& \Rightarrow K=\frac{k_1 k_2}{k_1+k_2}
\end{aligned}
\)
Time period is given by,
\(
T=2 \pi \sqrt{\frac{m}{K}}
\)
On substituting the respective values, we get: \(T=2 \pi \sqrt{\frac{m\left(k_1+k_2\right)}{k_1 k_2}}\)

Example 9: The spring shown in the figure below is unstretched when a man starts pulling on the cord. The mass of the block is \(M\). If the man exerts a constant force \(F\), find (a) the amplitude and the time period of the motion of the block, (b) the energy stored in the spring when the block passes through the equilibrium position and (c) the kinetic energy of the block at this position.

Solution:

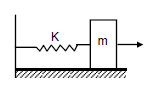
(a) We know-
\(
\begin{gathered}
\quad f=k x \\
\Rightarrow x=\frac{F}{k} \\
\text { Acceleration }=\frac{F}{m}
\end{gathered}
\)
Using the relation of time period of S.H.M.,
Time period, \(T=2 \pi \sqrt{\frac{\text { Displacement }}{\text { Acceleration }}}\)
\(
=2 \pi \sqrt{\frac{\left(\frac{F}{k}\right)}{\left(\frac{F}{m}\right)}}=2 \pi \sqrt{\frac{m}{k}}
\)
Amplitude = Maximum displacement \(=\frac{F}{k}\)
(b) When the block passes through the equilibrium position, the energy contained by the spring is given by,
\(
E=\frac{1}{2} k x^2=\frac{1}{2} k\left(\frac{F}{k}\right)^2=\frac{1}{2}\left(\frac{F^2}{k}\right)
\)
(c) At the mean position, potential energy is zero.
Kinetic energy is given by,
\(
\frac{1}{2} k x^2=\frac{1}{2} \frac{F^2}{k}
\)