Past NEET Papers
Quiz Summary
0 of 49 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 49 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 49
1. Question
Match Column I with Column II and choose the correct match from the given choices. [NEET 2021]
\(
\begin{array}{llcc}
\hline {\text { Column I }} & & \text { Column II } \\
\hline \text { A. } \begin{array}{l}
\text { Root mean square of } \\
\text { gas molecules }
\end{array} & 1 . & \frac{1}{3} n m \bar{v}^2 \\
\hline \text { B. } \begin{array}{l}
\text { Pressure exerted by } \\
\text { ideal gas }
\end{array} & 2 . & \sqrt{\frac{3 R T}{M}} \\
\hline \text { C. } \begin{array}{l}
\text { Average kinetic } \\
\text { energy of a molecule }
\end{array} & 3 . & \frac{5}{2} R T \\
\hline \text { D. } \begin{array}{l}
\text { Total internal energy } \\
\text { of 1 mole of a } \\
\text { diatomic gas }
\end{array} & 4 . & \frac{3}{2} k_B T \\
\hline
\end{array}
\)CorrectIncorrectHint
We know that, the rms speed of the gas molecules,
\(
v_{\mathrm{rms}}=\sqrt{3 R T / M}
\)
Here, \(T\) is the temperature of the gas, \(R\) is the universal gas constant, \(M\) is the molar mass of the gas. Pressure exerted by an ideal gas,
\(
p=\frac{1}{3} n m \bar{v}^2
\)
Here, \(n\) is the number of moles, \(m\) is the mass of the gas, \(\bar{v}\) is the average speed of the gas molecules.
The average kinetic energy of a molecule,
\(
K E_{a v}=\frac{3}{2} k_B T
\)
Here, \(k_B\) is the Boltzmann constant, \(T\) is the temperature of the gas.
For diatomic gas, degree of freedom, \(f=5\)
As, total internal energy of 1 mole of diatomic gas,
\(
\begin{aligned}
\Delta U & =\frac{n f R T}{2} \\
\Rightarrow \Delta U & =\frac{1(5) R T}{2} \Rightarrow \Delta U=\frac{5 R T}{2}
\end{aligned}
\)
The correct match is \(A \rightarrow 2, B \rightarrow 1, C \rightarrow 4\) and \(D \rightarrow 3\). -
Question 2 of 49
2. Question
The mean free path \(l\) for a gas molecule depends upon diameter, \(d\) of the molecule as [NEET (Oct.) 2020]
CorrectIncorrectHint
The mean free path \(l\) for a gas molecule is given as
\(
l=\frac{1}{\sqrt{2} \pi n d^2} \Rightarrow l \propto \frac{1}{d^2}
\)
where, \(d=\) diameter of molecule of gas. -
Question 3 of 49
3. Question
An ideal gas equation can be written as \(p=\frac{\rho R T}{M_0}\) where, \(\rho\) and \(M_0\) are respectively, [NEET (Oct.) 2020]
CorrectIncorrectHint
Ideal gas equation is given as
\(
\begin{aligned}
\qquad p & =\frac{\rho R T}{M_0} \Rightarrow p \cdot \frac{M_0}{\rho}=R T \\
\Rightarrow \quad p V & =R T \\
\text { where, } V & =\frac{M_0}{\rho}
\end{aligned}
\)
Hence, \(\rho\) and \(M_0\) are mass density and mass of gas, respectively. -
Question 4 of 49
4. Question
The mean free path \(\lambda\) for a gas, with molecular diameter \(d\) and number density \(n\) can be expressed as [NEET (Sep.) 2020]
CorrectIncorrectHint
The mean free path \(\lambda\) for a gas, with molecular diameter d and number density \(n\) is given by the relation
\(
\lambda=\frac{1}{\sqrt{2} n \pi d^2}
\)
Hence, the correct option is (a). -
Question 5 of 49
5. Question
A cylinder contains hydrogen gas at pressure of \(249 \mathrm{kPa}\) and temperature \(27^{\circ} \mathrm{C}\). Its density is \(\left(R=8.3 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}\right)\) [NEET (Sep.) 2020]
CorrectIncorrectHint
Given,
pressure \(p=249 \mathrm{kPa}=249 \times 10^3 \mathrm{~Pa}\)
Temperature, \(T=27^{\circ} \mathrm{C}\)
\(
=273+27 \mathrm{~K}=300 \mathrm{~K}
\)
Density, \(\rho=\) ?
As, from ideal gas equation,
\(
p V=n R T
\)
\(
\begin{aligned}
& \Rightarrow \quad p V=\frac{m}{M} R T \quad\left[\text { as } n=\frac{m}{M}\right] \\
& \Rightarrow \quad p V M=m R T \\
& \Rightarrow \quad p M=\frac{m}{V} R T=\rho R T \quad\left[\text { as } \frac{m}{V}=\rho\right] \\
&
\end{aligned}
\)
\(
\begin{aligned}
& \begin{aligned}
& \Rightarrow \quad \rho=\frac{p M}{R T} \\
&=\frac{249 \times 10^3 \times 2 \times 10^{-3}}{8.3 \times 300} \\
& {\left[\because \text { for hydrogen gas, } M=2 \mathrm{~g}=2 \times 10^{-3} \mathrm{~kg}\right] }
\end{aligned} \\
& \Rightarrow \rho=0.2 \mathrm{~kg} / \mathrm{m}^3
\end{aligned}
\)
Hence, the correct option is (a). -
Question 6 of 49
6. Question
The average thermal energy for a monoatomic gas is (where, \(k_B\) is Boltzmann constant and \(T\) is absolute temperature.) [NEET (Sep.) 2020]
CorrectIncorrectHint
The average thermal energy of a system with degree of freedom \(f\) is equals to its average energy, which is given as
\(
=\frac{f}{2} k_B \cdot T
\)
For monoatomic gas, \(f=3\)
\(\therefore\) Average thermal energy \(=\frac{3}{2} k_B \cdot T\)
Hence, the correct option is (a). -
Question 7 of 49
7. Question
Increase in temperature of a gas-filled in a container would lead to [NEET (National) 2019]
CorrectIncorrectHint
As the temperature of the gas in the container is increased, the kinetic energy also increases. This is because the average kinetic energy of a gas is given by
\(
\mathrm{KE}=\frac{f}{2} n R T \dots(i)
\)
where, \(f=\) degree of freedom,
\(n=\) number of moles of gas molecules,
\(R=\) universal gas constant, and
\(T=\) absolute temperature of the gas.
From Eq. (i),
\(
\mathrm{KE} \propto T
\)
option (b) is incorrect as the increase in temperature will lead to an increase in pressure as \(p \propto T\). Other options (c) and (d) are also incorrect as molecular distance increases while mass remains the same for the increase in temperature. -
Question 8 of 49
8. Question
The value of \(\gamma\left(=\frac{C_p}{C_v}\right)\), for hydrogen, helium and another ideal diatomic gas X (whose molecules are not rigid but have an additional vibrational mode), are respectively equal to [NEET (Odisha) 2019]
CorrectIncorrectHint
The poisson’s ratio,
\(
\gamma=\frac{C_P}{C_V} \dots(i)
\)
where, \(C_p=\) molar heat capacity constant pressure
and \(C_V=\) molar heat capacity at constant volumeAlso, \(C_p=C_v+R\) (from Mayer’s relation)
\(
\begin{aligned}
& C_v=\frac{f}{2} R \quad \text { (where, } f=\text { degree of freedom) } \\
& \Rightarrow C_p=\left(\frac{f}{2}+1\right) R \\
& \text { So, Eq. (i) becomes, } \\
& \Rightarrow \gamma=1+\frac{2}{f}
\end{aligned}
\)
For hydrogen gas, which is diatomic, the degree of freedom is 5 (3 translational, 2 rotational).
\(
\therefore \quad \gamma=1+\frac{2}{5}=\frac{7}{5}
\)
For helium gas, which is monoatomic, the degree of freedom is 3 (3 translational only).
\(
\therefore \quad \gamma=1+\frac{2}{3}=\frac{5}{3}
\)
The diatomic gas \(X\) also have vibrational motion, so degree of freedom is 7 (3 translational, 2 rotational and 2 vibrational).
\(
\therefore \quad \gamma=1+\frac{2}{7}=\frac{9}{7}
\) -
Question 9 of 49
9. Question
At what temperature will the rms speed of oxygen molecules become just sufficient for escaping from the Earth’s atmosphere? (Given: mass of oxygen molecule, \(\mathrm{m}=2.76 \times 10^{-26} \mathrm{~kg}\), Boltzmann’s constant \(k_B=1.38 \times 10^{-23} \mathrm{~J} \mathrm{~K}^{-1}\) ) [NEET 2018]
CorrectIncorrectHint
Key Concept The minimum velocity with which the body must be projected vertically upwards, so that it could escape from the Earth’s atmosphere, is its escape velocity \(\left(v_e\right)\).
As, \(v_e=\sqrt{2 g R}\)
Substituting the value of \(g\left(9.8 \mathrm{~ms}^{-2}\right)\) and radius of Earth \(\left(R=6.4 \times 10^6 \mathrm{~m}\right)\), we get
\(
\begin{aligned}
v_e & =\sqrt{2 \times 9.8 \times 6.4 \times 10^6} \\
& \cong 11.2 \mathrm{~km} \mathrm{~s}^{-1}=11200 \mathrm{~m} \mathrm{~s}^{-1}
\end{aligned}
\)
Let the temperature of molecule beT when it attains \(v_e\).
According to the question,
\(
v_{\mathrm{rms}}=v_e
\)
where, \(v_{\mathrm{rms}}\) is the rms speed of the oxygen molecule.
\(
\begin{array}{ll}
\Rightarrow \quad \sqrt{\frac{3 k_B T}{\mathrm{~m}_{\mathrm{O}_2}}}=11.2 \times 10^3 \\
\text { or } & T=\frac{\left(11.2 \times 10^3\right)^2\left(\mathrm{~m}_{\mathrm{O}_2}\right)}{\left(3 k_B\right)}
\end{array}
\)
Substituting the given values, i.e.,
\(
\begin{aligned}
& R_B=1.38 \times 10^{-23} \mathrm{JK}^{-1} \text { and } \\
& m_{\mathrm{O}_2}=m=2.76 \times 10^{-26} \mathrm{~kg}
\end{aligned}
\)
We get,
\(
\begin{aligned}
T & =\frac{\left(11.2 \times 10^3\right)^2\left(2.76 \times 10^{-26}\right)}{\left(3 \times 1.38 \times 10^{-23}\right)} \\
& =8.3626 \times 10^4 \mathrm{~K}
\end{aligned}
\) -
Question 10 of 49
10. Question
A gas mixture consists of 2 moles of \(\mathrm{O}_2\) and 4 moles of \(\mathrm{Ar}\) at temperature \(T\). Neglecting all vibrational modes, the total internal energy of the system is [NEET 2017]
CorrectIncorrectHint
(d)
The total internal energy of system \(=\) Internal energy of oxygen molecules + Internal energy of argon molecules
\(
\begin{aligned}
& =\frac{f_1}{2} n_1 R T+\frac{f_2}{2} n_2 R T=\frac{5}{2} \times 2 R T+\frac{3}{2} \times 4 R T \\
& =11 R T
\end{aligned}
\) -
Question 11 of 49
11. Question
The molecules of a given mass of a gas have r.m.s. velocity of \(200 \mathrm{~ms}^{-1}\) at \(27^{\circ} \mathrm{C}\) and \(1.0 \times 10^5\) \(\mathrm{Nm}^{-2}\) pressure. When the temperature and pressure of the gas are respectively, \(127^{\circ} \mathrm{C}\) and \(0.05 \times 10^5 \mathrm{Nm}^{-2}\), the r.m.s. velocity of its molecules in \(\mathrm{ms}^1\) is: [NEET 2016]
CorrectIncorrectHint
Here \(\mathrm{v}_1=200 \mathrm{~m} / \mathrm{s}\);
temperature \(\mathrm{T}_1=27^{\circ} \mathrm{C}=27+273=300 \mathrm{k}\)
temperature \(\mathrm{T}_2=127^{\circ} \mathrm{C}=127+273=400 \mathrm{k}, \mathrm{v}_2=\) ?
R.M.S. Velocity, \(\mathrm{v} \propto \sqrt{T}\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{\mathrm{v}_2}{200}=\sqrt{\frac{400}{300}} \\
& \Rightarrow \quad \mathrm{v}_2=\frac{200 \times 2}{\sqrt{3}} \mathrm{~m} / \mathrm{s} \Rightarrow \mathrm{v}_2=\frac{400}{\sqrt{3}} \mathrm{~m} / \mathrm{s}
\end{aligned}
\) -
Question 12 of 49
12. Question
A given sample of an ideal gas occupies a volume \(V\) at a pressure p and absolute temperature \(T\). The mass of each molecule of the gas is \(\mathrm{m}\). Which of the following gives the density of the gas? [NEET 2016]
CorrectIncorrectHint
As we know that
Pressure, \(p=\frac{1}{3} \cdot \frac{n m}{V} v_{\mathrm{rms}}^2\)
\(\because n m=\) mass of the gas, \(V=\) volume of the gas
\(\therefore \frac{m n}{V}=\) density of the gas. Thus,
\(p=\frac{1}{2} p v_{\mathrm{rms}}^2=\frac{1}{3} \rho \frac{3 R T}{M_0}=\frac{\rho R T}{M_0}\)
\(
\left(\because v_{\mathrm{mms}}=\sqrt{\frac{3 R T}{M_0}}\right)
\)
\(
\begin{aligned}
& \rho=\frac{p M_0}{R T}=\frac{p m N_A}{k N_A T} \\
& {\left[\because R=N_A k \text { and } M_0=m N_A\right]} \\
& \rho=\frac{p m}{k T} \\
&
\end{aligned}
\) -
Question 13 of 49
13. Question
One mole of an ideal monatomic gas undergoes a process described by the equation \(p V^3=\) constant. The heat capacity of the gas during this process is [NEET 2016]
CorrectIncorrectHint
As we know that for polytropic process of index \(\alpha\) specific heat capacity
\(
\begin{aligned}
& \qquad=C_v+\frac{R}{1-\alpha} \\
& \because \text { Process, } \rho V^3=\text { constant } \Rightarrow \alpha=3 \\
& \therefore \quad C=C_v+\frac{R}{1-\alpha}=\frac{f R}{2}+\frac{R}{1-3} \\
& \text { where, } C_v=\frac{f R}{2}=\frac{3 R}{2}
\end{aligned}
\)
For monatomic gas, \(f=3=\frac{3 R}{2}\)
\(
\Rightarrow \quad C=\frac{3 R}{2}-\frac{R}{2}=R
\) -
Question 14 of 49
14. Question
\(4.0 \mathrm{~g}\) of a gas occupies 22.4 litres at NTP. The specific heat capacity of the gas at constant volume is \(5.0 \mathrm{JK}^{-1}\). If the speed of sound in this gas at NTP is \(952 \mathrm{~ms}^{-1}\), then the heat capacity at constant pressure is (Take gas constant \(\mathrm{R}=\) [CBSE AIPMT 2015]
CorrectIncorrectHint
Molar mass of the gas \(=4 \mathrm{~g} / \mathrm{mol}\) Speed of sound
\(
\begin{aligned}
& \mathrm{v}=\sqrt{\frac{\gamma \mathrm{RT}}{\mathrm{m}}} \Rightarrow 952=\sqrt{\frac{\gamma \times 3.3 \times 273}{4 \times 10^{-3}}} \\
& \Rightarrow \gamma=1.6=\frac{16}{10}=\frac{8}{5} \\
& \text { Also, } \gamma=\frac{\mathrm{C}_{\mathrm{P}}}{\mathrm{C}_{\mathrm{V}}}=\frac{8}{5}
\end{aligned}
\)
So, \(\mathrm{C}_{\mathrm{P}}=\frac{8 \times 5}{5}=8 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}\)
\(
\left[\mathrm{C}_{\mathrm{V}}=5.0 \mathrm{JK}^{-1} \text { given }\right]
\) -
Question 15 of 49
15. Question
Two vessels separately contain two ideal gases \(A\) and \(B\) at the same temperature. The pressure of A being twice that of B. Under such conditions, the density of \(\mathrm{A}\) is found to be 1.5 times the density of \(B\). The ratio of molecular weight of \(A\) and \(B\) is: [CBSE AIPMT 2015]
CorrectIncorrectHint
From \(\mathrm{PV}=\mathrm{nRT}\)
\(
P_A-\frac{\rho_A M_A}{R T} \text { and } P_B=\frac{\rho_B M_B}{R T}
\)
From question,
\(
\frac{P_{\mathrm{A}}}{\mathrm{P}_{\mathrm{B}}}=\frac{\rho_{\mathrm{A}}}{\rho_{\mathrm{B}}} \frac{\mathrm{M}_{\mathrm{A}}}{\mathrm{M}_{\mathrm{B}}}=2 \frac{\mathrm{M}_{\mathrm{A}}}{\mathrm{M}_{\mathrm{B}}}=\frac{3}{2}
\)
So, \(\frac{\mathrm{M}_{\mathrm{A}}}{\mathrm{M}_{\mathrm{B}}}=\frac{3}{4}\) -
Question 16 of 49
16. Question
The ratio of the specific heats \(\frac{\mathrm{C}_{\mathrm{p}}}{\mathrm{C}_v}=\gamma\) in terms of degrees of freedom (n) is given by [CBSE AIPMT 2015]
CorrectIncorrectHint
The specific heat of gas at constant volume in terms of degree of freedom \(n\) is
\(
C_v=\frac{n}{2} R
\)
Also C \(_p-C_v=R\)
\(
\begin{aligned}
& C_p=\frac{n}{2} R+R=R\left(1+\frac{n}{2}\right) \\
& \gamma=\frac{C_p}{C_v}=\frac{R\left(1+\frac{n}{2}\right)}{\frac{n}{2} R}=\frac{2}{n}+1
\end{aligned}
\) -
Question 17 of 49
17. Question
One mole of an ideal diatomic gas undergoes a transition from \(A\) to \(B\) along a path \(A B\) as shown in the figure. The change in internal energy of the gas during the transition is: [CBSE AIPMT 2015]
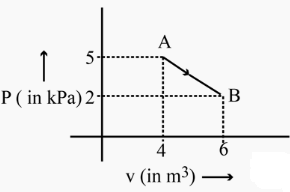 CorrectIncorrect
CorrectIncorrectHint
Change in internal energy from \(\mathrm{A} \rightarrow \mathrm{B}[latex]
[latex]
\begin{aligned}
& \Delta \mathrm{U}=\frac{\mathrm{f}}{2} \mathrm{nR} \Delta \mathrm{T}=\frac{\mathrm{f}}{2} \mathrm{nR}\left(\mathrm{T}_{\mathrm{f}}-\mathrm{T}_{\mathrm{i}}\right) \\
& =\frac{5}{2}\left\{\mathrm{P}_{\mathrm{f}} \mathrm{V}_{\mathrm{f}}-\mathrm{P}_{\mathrm{i}} \mathrm{V}_{\mathrm{i}}\right\} \\
& =\frac{5}{2}\left\{2 \times 10^3 \times 6-5 \times 10^3 \times 4\right\} \\
& =\frac{5}{2}\{12-20\} \times 10^3 \mathrm{~J}=5 \times(-4) \times 10^3 \mathrm{~J} \\
& \Delta \mathrm{U}=-20 \mathrm{KJ}
\end{aligned}
\)
(As gas is diatomic \(\, therefore, f=5\) ) -
Question 18 of 49
18. Question
The mean free path of molecules of a gas, (radius ‘ \(r\) ‘) is inversely proportional to: [CBSE AIPMT 2014]
CorrectIncorrectHint
Mean free path \(\lambda_{\mathrm{m}}=\frac{1}{\sqrt{2} \pi \mathrm{d}^2 \mathrm{n}}\) where \(\mathrm{d}=\) diameter of molecule and \(\mathrm{d}=2 \mathrm{r}\)
\(
\therefore \quad \lambda_{\mathrm{m}} \propto \frac{1}{\mathrm{r}^2}
\) -
Question 19 of 49
19. Question
The molar-specific heats of an ideal gas at constant pressure and volume are denoted by \(C_p\) and \(C_v\) respectively. If \(\gamma=\frac{C_p}{C_v}\) and \(R\) is the universal gas constant, then \(C_v\) is equal to [NEET 2013]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (a) } \mathrm{C}_{\mathrm{p}}-\mathrm{C}_{\mathrm{v}}=\mathrm{R} \Rightarrow \mathrm{C}_{\mathrm{p}}=\mathrm{C}_{\mathrm{v}}+\mathrm{R} \\
& \because \gamma=\frac{\mathrm{C}_{\mathrm{p}}}{\mathrm{C}_{\mathrm{v}}}=\frac{\mathrm{C}_{\mathrm{v}}+\mathrm{R}}{\mathrm{C}_{\mathrm{v}}}=\frac{\mathrm{C}_{\mathrm{v}}}{\mathrm{C}_{\mathrm{v}}}+\frac{\mathrm{R}}{\mathrm{C}_{\mathrm{v}}} \\
& \Rightarrow \gamma=1+\frac{\mathrm{R}}{\mathrm{C}_{\mathrm{v}}} \Rightarrow \frac{\mathrm{R}}{\mathrm{C}_{\mathrm{v}}}=\gamma-1 \\
& \Rightarrow \mathrm{C}_{\mathrm{v}}=\frac{\mathrm{R}}{\gamma-1}
\end{aligned}
\) -
Question 20 of 49
20. Question
In the given \((V-T)\) diagram, what is the relation between pressures \(p_1\) and \(p_2\)? [NEET 2013]
CorrectIncorrectHint
According to the question,
Slope of the graph \(\propto \frac{1}{\text { Pressure } p}\)
So, \(p_2<p_1\)Note:
As \(V=\) constant \(\Rightarrow P \propto T\)
Hence from \(\mathrm{V}-\mathrm{T}\) graph \(\mathrm{P}_1>\mathrm{P}_2\)
From the Gay – Lussac’s law, volume remain constant, the pressure of a given mass of a gas is directly proportional to its absolute temperature.
\(
\begin{aligned}
& \therefore \mathrm{P} \propto \mathrm{T} \\
& \frac{\mathrm{P}}{\mathrm{T}}=\text { constant } \Rightarrow \frac{\mathrm{P}_1}{\mathrm{~T}_1}=\frac{\mathrm{P}_2}{\mathrm{~T}_2}
\end{aligned}
\) -
Question 21 of 49
21. Question
During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its temperature. The ratio of \(\frac{C_p}{C_v}\) for the gas is [NEET 2013]
CorrectIncorrectHint
According to question,
\(
p \propto T^3 \dots(i)
\)
\(
\left(\begin{array}{l}
p=\text { pressure } \\
T=\text { temperature }
\end{array}\right)
\)
and we know that
\(
p V=n R T \text { and } p V \propto T \dots(ii)
\)
So, putting Eq. (ii) in (i),
\(
\begin{array}{lc}
& p \propto(p V)^3 \\
\Rightarrow & p^2 V^3=\text { constant } \\
\Rightarrow & p V^{3 / 2}=\text { constant } \dots(iii)
\end{array}
\)
\(\Rightarrow\) Comparing Eq. (iii) with
pV \(\gamma=\) constant.
We have \(\gamma=3 / 2\) -
Question 22 of 49
22. Question
The amount of heat energy required to raise the temperature of \(1 \mathrm{~g}\) of Helium at NTP, from \(\mathrm{T}_1 \mathrm{~K}\) to \(\mathrm{T}_2 \mathrm{~K}\) is [NEET 2013]
CorrectIncorrectHint
From first law of thermodynamics
\(
\begin{aligned}
& \Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W}=\frac{3}{2} \cdot \frac{1}{4} \mathrm{R}\left(\mathrm{T}_2-\mathrm{T}_1\right)+0 \\
& =\frac{3}{8} \mathrm{~N}_{\mathrm{a}} \mathrm{K}_{\mathrm{B}}\left(\mathrm{T}_2-\mathrm{T}_1\right)\left[\because \mathrm{K}=\frac{\mathrm{R}}{\mathrm{N}}\right]
\end{aligned}
\) -
Question 23 of 49
23. Question
In a vessel, the gas is at a pressure \(P\). If the mass of all the molecules is halved and their speed is doubled, then the resultant pressure will be [NEET Karnataka 2013]
CorrectIncorrectHint
\(P=\frac{1}{3} \frac{m N}{V} v_{\mathrm{rms}}^2\)
where \(\mathrm{m}=\) mass of each molecules
\(\mathrm{N}=\) total number of molecules
\(\mathrm{V}=\) volume of the gas
When the mass is halved and the speed is doubled then
\(
\text { Resultant pressure, } P^{\prime}=\frac{1}{3} \times\left(\frac{m}{2}\right) \times \frac{\mathrm{N}}{\mathrm{V}}\left(2 v_{\mathrm{ms}}\right)^2=2P
\) -
Question 24 of 49
24. Question
At \(10^{\circ} \mathrm{C}\) the value of the density of a fixed mass of an ideal gas divided by its pressure is \(x\). At \(110^{\circ} \mathrm{C}\) this ratio is: [CBSE AIPMT 2008]
CorrectIncorrectHint
Let the mass of the gas be \(\mathrm{m}\). At a fixed temperature and pressure, volume is fixed.
Density of the gas, \(\rho=\frac{\mathrm{m}}{\mathrm{V}}\)
\(
\begin{aligned}
& \text { Now } \frac{\rho}{\mathrm{P}}=\frac{\mathrm{m}}{\mathrm{PV}}=\frac{\mathrm{m}}{\mathrm{nRT}} \\
& \Rightarrow \frac{\mathrm{m}}{\mathrm{nRT}}=x \text { (By question) } \\
& \Rightarrow \mathrm{xT}=\text { constant } \Rightarrow \mathrm{x}_1 \mathrm{~T}_1=\mathrm{x}_2 \mathrm{~T}_2 \\
& \Rightarrow \mathrm{x}_2 \Rightarrow \frac{\mathrm{x}_1 \mathrm{~T}_1}{\mathrm{~T}_2}=\frac{283}{383} \mathrm{x}\left[\begin{array}{c}
\text { Given } \\
T_1=283 K \\
T_2=383 K
\end{array}\right]
\end{aligned}
\) -
Question 25 of 49
25. Question
The molar specific heat at a constant pressure of an ideal gas is (7/2)R. The ratio of specific heat at constant pressure to that at constant volume is [CBSE AIPMT 2006]
CorrectIncorrectHint
We have given molar specificheat at instant pressure
\(
C_p=\frac{7}{2} R
\)
Mayer’s relation can be written as :
Molar specificheat at constant pressure
– Molar specificheat at constant volume
\(=\) Gas constant,
i.e. \(C_p-C_v=R \Rightarrow C_v=C_p-R\)
\(
=\frac{7}{2} R-R=\frac{5}{2} R\left[\because C_p=\frac{7}{2} R\right]
\)
Hence, the required ratio is
\(
\gamma=\frac{C_p}{C_V}=\frac{\left(\frac{7}{2}\right) R}{\left(\frac{5}{2}\right) R}=\frac{7}{5}
\) -
Question 26 of 49
26. Question
The equation of state for \(5 \mathrm{~g}\) of oxygen at a pressure \(P\) and temperature \(T\), when occupying a volume \(\mathrm{V}\), will be [CBSE AIPMT 2004]
(where \(\mathrm{R}\) is the gas constant).
CorrectIncorrectHint
Number of moles,
\(
n=\frac{m}{\text { molecular weight }}=\frac{5}{32}
\)
As from ideal gas equation
\(
p V=n R T \Rightarrow p V=\frac{5}{32} R T
\) -
Question 27 of 49
27. Question
A gas at \(27^{\circ} \mathrm{C}\) temperature and 30 atmospheric pressure is allowed to expand to the atmospheric pressure. If the volume becomes 10 times its initial volume, then the final temperature becomes [CBSE AIPMT 2001]
CorrectIncorrectHint
Given: Initial temperature of gas
\(\left(T_1\right)=27^{\circ} \mathrm{C}=300 \mathrm{~K}\)
Initial pressure \(\left(P_1\right)=30 \mathrm{~atm}\)
Initial volume \(\left(V_1\right)=V\)
Final pressure \(\left(P_2\right)=1 \mathrm{~atm}\)
Final volume \(\left(V_2\right)=10 \mathrm{~V}\).
We know from the general gas equation that
\(
\begin{aligned}
& \frac{P_1 V_1}{T_1}=\frac{P_2 V_2}{T_2} \quad \text { or, } \frac{30 \times V}{300}=\frac{1 \times 10 \mathrm{~V}}{T_2} \\
& \text { or, } T_2=100 \mathrm{~K}=-173^{\circ} \mathrm{C} .
\end{aligned}
\) -
Question 28 of 49
28. Question
If \(\gamma\) be the ratio of specific heats of a perfect gas, the number of degrees of freedom of a molecule of the gas is [CBSE AIPMT 2000]
CorrectIncorrectHint
We know that ratio of specific heat,
\(
\gamma=1+\frac{2}{n} \text { or } n=\frac{2}{\gamma-1}
\)
[where \(\mathrm{n}=\) Degree of freedom] -
Question 29 of 49
29. Question
The gases carbon-monoxide (CO) and nitrogen at the same temperature have kinetic energies \(E_1\) and \(E_2\) respectively. Then [CBSE AIPMT 2000]
CorrectIncorrectHint
The gases carbon-monoxide \((\mathrm{CO})\) and nitrogen \(\left(\mathrm{N}_2\right)\) are diatomic, so both have equal kinetic energy \(\frac{5}{2} k T\), i.e. \(E_1=E_2\).
-
Question 30 of 49
30. Question
An ideal gas at \(27^{\circ} \mathrm{C}\) is compressed adiabatically to \(\frac{8}{27}\) of its original volume. The rise in temperature is \(\left(\gamma=\frac{5}{3}\right)\) [CBSE AIPMT 1999]
CorrectIncorrectHint
In an adiabatic process
\(
\begin{aligned}
& p=\text { pressure } \\
& V=\text { volume }
\end{aligned}
\)
\(
\begin{aligned}
\gamma & =\text { atomicity of gas } \\
p V^\gamma & =\text { constant } \dots(i)
\end{aligned}
\)
Now from the ideal gas equation,
\(
p V=R T \quad \text { (for one mole) }
\)
or \(\quad p=\frac{R T}{V} \dots(ii)\)
\(
(R=\text { gas constant })
\)
From Eqs. (i) and (ii), we have
\(
\begin{aligned}
& \left(\frac{R T}{V}\right) V^\gamma=\text { constant } \\
& T V^{\gamma-1}=\text { constant } \dots(iii)
\end{aligned}
\)
So for two different cases of temperature and volume
So, \(T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1}\)
or \(\quad \frac{T_2}{T_1}=\left(\frac{V_1}{V_2}\right)^{\gamma-1} \dots(iv)\)
Given, \(\quad T_1=27^{\circ} \mathrm{C}\)
\(
=27+273=300 \mathrm{~K}
\)
Given, \(\quad \frac{V_2}{V_1}=\frac{8}{27}, \gamma=\frac{5}{3}\)
Substituting in Eq. (i), we get
\(
\frac{T_2}{300}=\left(\frac{27}{8}\right)^{5 / 3-1}
\)
or
\(
\frac{T_2}{300}=\left[\left(\frac{3}{2}\right)^3\right]^{2 / 3}
\)
or \(\quad \frac{T_2}{300}=\left(\frac{3}{2}\right)^2=\frac{9}{4}\)
\(
\therefore T_2=\frac{9}{4} \times 300=675 \mathrm{~K}=402^{\circ} \mathrm{C}
\)
Thus, rise in temperature
\(
=T_2-T_1=402-27=375^{\circ} \mathrm{C}
\) -
Question 31 of 49
31. Question
The degree of freedom of a molecule of a triatomic gas is [CBSE AIPMT 1999]
CorrectIncorrectHint
No. of degree of freedom \(=3 K-N\) where \(K\) is no. of atom and \(N\) is the number of relations between atoms. For triatomic gas, \(K=3, N={ }^3 C_2=3\)
No. of degree of freedom \(=3(3)-3=6\) -
Question 32 of 49
32. Question
At \(0 \mathrm{~K}\), which of the following properties of a gas will be zero? [CBSE AIPMT 1996]
CorrectIncorrectHint
At \(0 \mathrm{~K}\), molecular motion stops. Hence, the kinetic energy of molecules becomes zero.
-
Question 33 of 49
33. Question
A diatomic gas initially at \(18^{\circ} \mathrm{C}\) is compressed adiabatically to one-eight of its original volume. The temperature after compression will be [CBSE AIPMT 1996]
CorrectIncorrectHint
According to adiabatic process the relation between temperature and volume is given by
\(
T V^{\gamma-1}=\text { constant }
\)
So, for two different cases
\(
\therefore \quad T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1} \dots(i)
\)
Given, initial temperature
\(
T_1=18^{\circ} \mathrm{C}=291 \mathrm{~K}
\)
Let initial volume \(V_1=V\)
and final volume \(V_2=\left(\frac{1}{8}\right) V\)
Putting these values in Eq. (i)
\(
\begin{aligned}
T_2 & =291\left(\frac{V_1}{V_2}\right)^{\gamma-1}=291\left(\frac{V}{\left(\frac{1}{8}\right) \mathrm{V}}\right)^{7 / 5-1} \\
& \left(\gamma=\frac{7}{5} \text { for diatomic gas }\right) \\
& =291 \times 2.297=668.4 \mathrm{~K}
\end{aligned}
\) -
Question 34 of 49
34. Question
The equation of state, corresponding to \(8 \mathrm{~g}\) of \(\mathrm{O}_2\) is [CBSE AIPMT 1994]
CorrectIncorrectHint
As per ideal gas equation \(\mathrm{PV}=\mathrm{nRT}\) where \(\mathrm{n}=\) number of moles
Also number of moles \((\mathrm{n})=\frac{\text { Total mass }}{\text { Molar mass }}\)
Total mass of oxygen \(=8 \mathrm{~g}\) and molar mass of \(\mathrm{O}_2=16 \times\) \(2=32\)
Therefore number of moles \((\mathrm{n})=\quad \frac{\text { Total mass }}{\text { Molar mass }}=\frac{8}{32}=\frac{1}{4}\)
Thus \(\mathrm{PV}=\mathrm{nRT}\)
\(
\mathrm{PV}=\frac{\mathrm{RT}}{4}
\) -
Question 35 of 49
35. Question
The temperature of a gas is raised from \(27^{\circ} \mathrm{C}\) to \(927^{\circ} \mathrm{C}\). The root mean square speed is [CBSE AIPMT 1994]
CorrectIncorrectHint
\(v_{\mathrm{rms}} \propto \sqrt{T}\)
As temperature increases from \(300 \mathrm{~K}\) to \(1200 \mathrm{~K}\) that is four times, so, \(v_{\mathrm{rms}}\) will be doubled. -
Question 36 of 49
36. Question
If \(C_s\) be the velocity of sound in air and \(C\) be the r.m.s velocity, then [CBSE AIPMT 1994]
CorrectIncorrectHint
Velocity of sound \(\left(C_S\right)=\sqrt{\frac{\gamma P}{\rho}}\)
R.M.S. velocity of gas molecules \((C)=\sqrt{\frac{3 P}{\rho}}\)
\(
\frac{C_s}{C}=\sqrt{\frac{\gamma P}{\rho} \times \frac{\rho}{3 P}}=\sqrt{\frac{\gamma}{3}} \Rightarrow C_s=C \times \sqrt{\frac{\gamma}{3}}
\) -
Question 37 of 49
37. Question
The number of translational degree of freedom for a diatomic gas is [CBSE AIPMT 1993]
CorrectIncorrectHint
Number of degree of freedom of a dynamical system is obtained by subtracting the number of independent relations from the total number of coordinates required to specify the positions of constituent particles of the system.
If \(A=\) number of particlesin the system, \(R=\) number of independent relations among the particles,
\(N=\) number of degree of freedom of the system, then
\(
N=3 A-R
\)
Each monoatomic, diatomic, and triatomic gas has three translatory degree of freedom. -
Question 38 of 49
38. Question
If for a gas, \(\frac{R}{C_v}=0.67\), this gas is made up of molecules which are [CBSE AIPMT 1992]
CorrectIncorrectHint
\(
C_V=\frac{R}{0.67}=1.5 R=\frac{3}{2} R
\)
This is the case of monoatomic gases. when \(\quad C_v=\frac{3}{2} R\)Note:
For a gas having \(f\) degree of freedom specific heat at constant volume, \(C_v=\frac{1}{2} f R\) specific heat at constant pressure,
\(
C_p=\left(\frac{f}{2}+1\right) R
\)
where, \(R=\) universal gas constant.Since \(\frac{R}{C_V}=0.67 \Rightarrow C_V=\frac{3}{2} R\), hence gas is monoatomic.
-
Question 39 of 49
39. Question
Relation between pressure \((P)\) and energy \((E)\) of a gas is [CBSE AIPMT 1991]
CorrectIncorrectHint
Pressure exerted by gas molecules is
\(
p=\frac{1}{3} \rho \bar{v}^2 \dots(i)
\)
where, \(\rho=\) density of gas
\(\bar{v}=\) average velocity of gas molecules or \(p=\frac{2}{3} n \cdot \frac{1}{2} m \bar{v}^2 \quad(\because \rho=m n)\) Now,\(\frac{1}{2} m \bar{v}^2=\) average kinetic energy of a gas molecule \((\overline{\mathrm{KE}})\) Therefore, \(p=\frac{2}{3} n \overline{\mathrm{KE}}\) If \(N\) is total number of gas molecules in volume \(V\), then
No of gas molecules per unit volume
\(
\begin{aligned}
n & =\frac{N}{V} \\
\therefore \quad p & =\frac{2}{3} \cdot \frac{N}{V}\left(\frac{1}{2} m \bar{v}^2\right) \\
\text { or } \quad p V & =\frac{2}{3} N(\overline{K E}) \quad\left[K E=\frac{1}{2} m \bar{v}^2\right]
\end{aligned}
\)
Also, from Eq. (i),
\(
p=\frac{2}{3} \cdot \frac{1}{2} \rho \bar{v}^2
\)
Now, \(\frac{1}{2} \rho \bar{v}^2=\) average kinetic energy of the gas per unit volume.
Therefore, \(p=\frac{2}{3} E\) -
Question 40 of 49
40. Question
Three containers of the same volume contain three different gases. The masses of the molecules are \(m_1, m_2\) and \(m_3\) and the number of molecules in their respective containers are \(N_1\), \(N_2\) and \(N_3\). The gas pressure in the containers are \(P_1, P_2\), and \(P_3\) respectively. All the gases are now mixed and put in one of these containers. The pressure \(P\) of the mixture will be [CBSE AIPMT 1991]
CorrectIncorrectHint
According to Dalton’s law of partial pressure, the total pressure exerted by a mixture of gases, which do not interact with each other, is equal to sum of the partial pressures which each would exert, if alone occupied the same volume at the given temperature. When gases are put in one container, then pressure \(p\) of the mixture will be
\(
p=p_1+p_2+p_3
\) -
Question 41 of 49
41. Question
\(\mathrm{N}\) molecules each of mass \(\mathrm{m}\) of a gas \(A\) and \(2 \mathrm{~N}\) molecules each of mass \(2 \mathrm{~m}\) of gas \(B\) are contained in the same vessel which is maintained at temperature \(T\). The mean square velocity of molecules of \(B\) type is \(v^2\) and the mean square rectangular component of the velocity of \(A\) type is denoted by \(\omega^2\). Then \(\omega^2 / v^2\) [CBSE AIPMT 1991]
CorrectIncorrectHint
The mean square velocity of A type molecules \(=\omega^2+\omega^2+\omega^2=3 \omega^2\)
Therefore, \(\frac{1}{2} m\left(3 \omega^2\right)=\frac{1}{2}(2 m) v^2\)
This gives \(\omega^2 / v^2=2 / 3\)
Mean kinetic energy of the two types of molecules should be equal. -
Question 42 of 49
42. Question
For hydrogen gas, \(C_p-C_v=\) a and for oxygen gas, \(C_p-C_v=b\), so the relation between a and b is given by [CBSE AIPMT 1991]
CorrectIncorrectHint
Both hydrogen and oxygen are diatomic gases and \(C_p-C_v=R\) is the same for all gases, hence \(a=b\).
-
Question 43 of 49
43. Question
According to kinetic theory of gases, at absolute zero temperature [CBSE AIPMT 1990]
CorrectIncorrectHint
The average kinetic energy of gas molecules is directly proportional to absolute temperature only; this implies that all molecular motion ceases if the temperature is reduced to absolute zero.
According to kinetic theory of gases, the pressure pexerted by one mole of an ideal gas is given by
\(
p=\frac{1}{3} \frac{M}{V} c^2 \text { or } p V=\frac{1}{3} M c^2
\)
or \(\quad \frac{1}{3} M c^2=R T \dots(i)\)
where \(c\) is root mean square velocity of gas.
From Eq. (i), when \(T=0, c=0\)
Hence, absolute zero of temperature may be defined as that temperature at which root mean square velocity of the gas molecules reduces to zero. It means molecular motion ceases at absolute zero. -
Question 44 of 49
44. Question
For a certain gas, the ratio of specific heats is given to be \(\gamma=1.5\). For this gas [CBSE AIPMT 1990]
CorrectIncorrectHint
\(
\begin{aligned}
& \gamma=\frac{C_P}{C_V}=\frac{15}{10}=\frac{3}{2} \Rightarrow C_V=\frac{2}{3} C_P \\
& C_P-C_V=\frac{R}{J} \Rightarrow C_P-\frac{2}{3} C_P=\frac{R}{J} \\
& \Rightarrow \frac{C_P}{3}=\frac{R}{J} \Rightarrow C_P=\frac{3 R}{J}
\end{aligned}
\) -
Question 45 of 49
45. Question
One mole of an ideal monoatomic gas requires \(207 \mathrm{~J}\) heat to raise the temperature by \(10 \mathrm{~K}\) when heated at constant pressure. If the same gas is heated at constant volume to raise the temperature by the same \(10 \mathrm{~K}\), the heat required is
[Given the gas constant \(R=8.3 \mathrm{~J} / \mathrm{mol}\). K] [CBSE AIPMT 1990]CorrectIncorrectHint
\(C_p=\frac{5}{2} R\) and \(C_v=\frac{3}{2} R\)
We know that \(Q_v=n C_v \Delta T\) and \(Q_p=n C_p \Delta T\)
\(
\Rightarrow \frac{Q_v}{Q_p}=\frac{3}{5}
\)
Given \(Q_p=207 \mathrm{~J} \Rightarrow Q_v \equiv 124 \mathrm{~J}\) -
Question 46 of 49
46. Question
At constant volume, the temperature is increased then [CBSE AIPMT 1989]
CorrectIncorrectHint
As the temperature increases, the average velocity increases. So, the collisions are faster.
-
Question 47 of 49
47. Question
A polyatomic gas with \(\mathrm{n}\) degrees of freedom has a mean energy per molecule given by [CBSE AIPMT 1989]
CorrectIncorrectHint
According to the law of equipartition of energy, the energy per degree of freedom is \(\frac{1}{2} k T\).
For a polyatomic gas with \(\mathrm{n}\) degrees of freedom, the mean energy per molecule \(=\frac{1}{2} n k T\)Alternate:
Concept If there is sudden compression without exchange of heat the process will be adiabatic.
According to law of equipartition of energy for any dynamical system in thermal equilibrium, the total energy is distributed equally amongst all the degrees of freedom and the energy associated with each molecule per degree of freedom is \(\frac{1}{2} k T\). For a polyatomic gas with \(n\) degrees of freedom the mean energy per molecule \(=\frac{1}{2} n k T\).
\(K=\) Boltzmann constant
\(n=\) degree of freedom
\(T=\) Temperature -
Question 48 of 49
48. Question
At \(27^{\circ} \mathrm{C}\) a gas is compressed suddenly such that its pressure becomes \(\left(\frac{1}{8}\right)\) of original pressure. Final temperature will be \(\left(\gamma=\frac{5}{3}\right)\) [CBSE AIPMT 1989]
CorrectIncorrectHint
The adiabatic relation between \(p\) and \(V\) for a perfect gas is
\(
\left.p V^\gamma=k \text { (a constant }\right) \dots(i)
\)
Again from standard gas equation
\(
p V=n R T \Rightarrow V=\frac{R T}{p}
\)
Putting in Eq. (i), we get
\(
p \frac{R^\gamma T^\gamma}{p^\gamma}=k
\)
or \(\quad p^{1-r} T^\gamma=\frac{k}{R^\gamma}=\) ano ther constant
i.e. \(p^{1-\gamma} T^\gamma=\) constant
Comparing two different situations,
\(
\begin{aligned}
& p_1^{1-\gamma} T_1^\gamma=p_2^{1-\gamma} T_2^\gamma \\
& \text { Here, } \quad p_2=\left(\frac{1}{8}\right) p_1 \\
& T_1=27^{\circ} \mathrm{C}=273+27=300 \mathrm{~K} \\
& T_2=?, \gamma=\frac{5}{3} \\
& \therefore\left(\frac{T_2}{T_1}\right)^\gamma=\left(\frac{p_1}{p_2}\right)^{1-\gamma} \\
& \text { or }\left(\frac{T_2}{300}\right)^{5 / 3}=(8)^{1-5 / 3}=(8)^{-2 / 3} \\
& \Rightarrow T_2=130.6 \mathrm{~K} \\
& \therefore \quad T_2=-142^{\circ} \mathrm{C} \\
&
\end{aligned}
\) -
Question 49 of 49
49. Question
Two containers A and B are partly filled with water and closed. The volume of \(A\) is twice that of \(B\) and it contains half the amount of water in B. If both are at the same temperature, the water vapour in the containers will have pressure in the ratio of [CBSE AIPMT 1988]
CorrectIncorrectHint
Vapour pressure does not depend on the amount of substance. It depends on the temperature alone. As both containers are at same temperature so vapour pressure of both A and B will be same hence ratio of vapour pressure is 1:1