Mean free path refers to the average distance that a moving particle travels between successive collisions or impacts. Furthermore, successive collisions result in modification of the moving particle’s energy or direction or any other particle properties. Moreover, the moving particle here refers to a molecule, an atom, or a photon.

How do we Measure Mean Free Path?

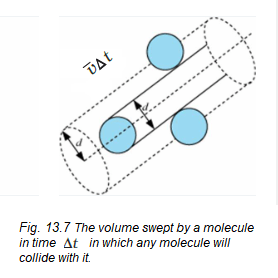
Let us assume the molecules of a gas are spheres of diameter \(d\). Focus on a single molecule with the average speed \(\langle v\rangle\). It will suffer a collision with any molecule that comes within a distance \(d\) between the centres. In time \(\Delta t\), it sweeps a volume \(\pi d^2\langle v\rangle\Delta t\) wherein any other molecule will collide with it (see Fig. 13.7). If \(n\) is the number of molecules per unit volume, the molecule suffers \(n \pi d^2\langle v\rangle\Delta t\) collisions in time \(\Delta t\). Thus the rate of collisions is \(n \pi d^2\langle v\rangle\) or the time between two successive collisions is on average,
\(
\tau=1 /\left(n \pi\langle v\rangle d^2\right) \dots(13.38)
\)
The average distance between two successive collisions, called the mean free path \(l\), is :
\(
l=\langle v\rangle \tau=1 /\left(n \pi d^2\right) \dots(13.39)
\)
In this derivation, we imagined the other molecules to be at rest. But actually, all molecules are moving and the collision rate is determined by the average relative velocity of the molecules. Thus we need to replace \(\langle v\rangle\) by \(\langle v_r\rangle\) in Eq. (13.38). A more exact treatment gives
\(
l=1 /\left(\sqrt{2} n \pi d^2\right) \dots(13.40)
\)
Let us estimate \(l\) and \(\tau\) for air molecules with average speeds \(\langle v\rangle=(485 \mathrm{~m} / \mathrm{s})\). At STP
\(
\begin{aligned}
& n=\frac{\left(0.02 \times 10^{23}\right)}{\left(22.4 \times 10^{-3}\right)} \\
& =2.7 \times 10^{25} \mathrm{~m}^{-3} . \\
& \text { Taking, } d=2 \times 10^{-10} \mathrm{~m}, \\
& \tau=6.1 \times 10^{-10} \mathrm{~s} \\
& \text { and } l=2.9 \times 10^{-7} \mathrm{~m} \approx 1500 d \dots(13.41)
\end{aligned}
\)

As expected, the mean free path given by Eq. (13.40) depends inversely on the number density and the size of the molecules. In a highly evacuated tube \(n\) is rather small and the mean free path can be as large as the length of the tube.

Example 1: Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at 2.0 atm and temperature \(17^{\circ} \mathrm{C}\). Take the radius of a nitrogen molecule to be roughly 1 Å. Compare the collision time with the time the molecule moves freely between two successive collisions (Molecular mass of \(\mathrm{N}_2=\) \(28.0 \mathrm{u})\)

Solution:

Use the formula for mean free path:
\(
\bar{l}=\frac{1}{\sqrt{2} \pi n d^2}
\)
where \(d\) is the diameter of a molecule. For the given pressure and temperature \(N / V=5.10 \times 10^{25} \mathrm{~m}^{-3}\) and \(=1.0 \times 10^{-7} \mathrm{~m} . v_{\mathrm{rms}}=5.1 \times 10^2 \mathrm{~m} \mathrm{~s}^{-1}\).
collisional frequency \(=\frac{v_{\mathrm{rms}}}{\bar{l}}=5.1 \times 10^9 \mathrm{~s}^{-1}\). Time taken for the collision \(=d / v_{\mathrm{rms}}=4 \times 10^{-13} \mathrm{~s}\).
Time taken between successive collisions \(=1 / v_{\text {rms }}=2 \times 10^{-10} \mathrm{~s}\). Thus the time taken between successive collisions is 500 times the time taken for a collision. Thus a molecule In a gas moves essentially free for most of the time.

Example 2: A metre long narrow bore held horizontally (and closed at one end) contains a \(76 \mathrm{~cm}\) long mercury thread, which traps a \(15 \mathrm{~cm}\) column of air. What happens if the tube is held vertically with the open end at the bottom?

Solution:

Length of the narrow bore, \(L=1 \mathrm{~m}=100 \mathrm{~cm}\)
Length of the mercury thread, \(l=76 \mathrm{~cm}\)
Length of the air column between mercury and the closed end, \(l_a=15 \mathrm{~cm}\)
Since the bore is held vertically in the air with the open end at the bottom, the mercury length that occupies the air space is: \(100-(76+15)=9 \mathrm{~cm}\)
Hence, the total length of the air column \(=15+9=24 \mathrm{~cm}\)
Let \(h \mathrm{~cm}\) of mercury flow out as a result of atmospheric pressure.
\(\therefore\) Length of the air column in the bore \(=24+h \mathrm{~cm}\)
And, length of the mercury column \(=76-h \mathrm{~cm}\)
Initial pressure, \(P_1=76 \mathrm{~cm}\) of mercury
Initial volume, \(V_1=15 \mathrm{~cm}^3\)
Final pressure, \(P_2=76-(76-h)=h \mathrm{~cm}\) of mercury
Final volume, \(V_2=(24+h) \mathrm{cm}^3\)
The temperature remains constant throughout the process.
\(
\begin{aligned}
& \therefore P_1 V_1=P_2 V_2 \\
& 76 \times 15=h(24+h) \\
& h^2+24 h-1140=0 \\
& \therefore h=\frac{-24 \pm \sqrt{(24)^2+4 \times 1 \times 1140}}{2 \times 1} \\
& =23.8 \mathrm{~cm} \text { or }-47.8 \mathrm{~cm}
\end{aligned}
\)
Height cannot be negative. Hence, \(23.8 \mathrm{~cm}\) of mercury will flow out from the bore and \(52.2 \mathrm{~cm}\) of mercury will remain in it. The length of the air column will be \(24+23.8=47.8 \mathrm{~cm}\).

Example 3: From a certain apparatus, the diffusion rate of hydrogen has an average value of \(28.7 \mathrm{~cm}^3 \mathrm{~s}^{-1}\). The diffusion of another gas under the same conditions is measured to have an average rate of \(7.2 \mathrm{~cm}^3 \mathrm{~s}^{-1}\). Identify the gas.
[Hint: Use Graham’s law of diffusion: \(R_1 / R_2=\left(M_2 / M_1\right)^{1 / 2}\), where \(R_1, R_2\) are diffusion rates of gases 1 and 2, and \(M_1\) and \(M_2\) their respective molecular masses. The law is a simple consequence of the kinetic theory.]

Solution:

According to Graham’s law of diffusion of gases, the rate of diffusion of a gas is inversely proportional to the square root of its molecular mass.
If \(R_1\) and \(R_2\) be the rates of diffusion of two gases having molecular masses \(M_1\) and \(M_2\) respectively, then
\(
\frac{R_1}{R_2}=\sqrt{\frac{M_2}{M_1}}
\)
Now \(R_1=28.7 \mathrm{~cm}^3 \mathrm{~s}^{-1}, R_2=7.2 \mathrm{~cm}^3 \mathrm{~s}^{-1}, M_1=2, M_2=\)?
\(
\therefore \frac{28.7}{7.2}=\sqrt{\frac{M_2}{2}}
\)
or \(\frac{M_2}{2}=\frac{28.7 \times 28.7}{7.2 \times 7.2}\)
or \(M_2=\frac{2 \times 28.7 \times 28.7}{7.2 \times 7.2}=31.78 \approx 32\)
This molecular mass of oxygen. Therefore the second gas is oxygen.

Example 4: A gas in equilibrium has uniform density and pressure throughout its volume. This is strictly true only if there are no external influences. A gas column under gravity, for example, does not have uniform density (and pressure). As you might expect, its density decreases with height. The precise dependence is given by the so-called law of the atmosphere
\(
n_2=n_1 \exp \left[-m g\left(h_2-h_1\right) / k_B T\right]
\)
where \(n_2, n_1\) refer to number density at heights \(h_2\) and \(h_1\) respectively. Use this relation to derive the equation for the sedimentation equilibrium of a suspension in a liquid column:
\(
n_2=n_1 \exp \left[-m g N_A\left(\rho-\rho^{\prime}\right)\left(h_2-h_1\right) /(\rho R T)\right]
\)
where \(\rho\) is the density of the suspended particle, and \(\rho^{\prime}\), that of the surrounding medium. [ \(N_{\mathrm{A}}\) is Avogadro’s number, and \(R\) the universal gas constant.] [Hint: Use Archimedes’ principle to find the apparent weight of the suspended particle.]

Solution:

According to the law of atmospheres, we have:
\(
n_2=n_1 \exp \left[-m g\left(h_2-h_1\right) / k B T\right] \ldots \text { (i) }
\)
Where,
\(n_1\) is the number density at height \(h_1\), and \(n_2\) is the number density at height \(h_2\)
\(\mathrm{mg}\) is the weight of the particle suspended in the gas column
Density of the medium \(=\rho^{\prime}\)
Density of the suspended particle \(=\rho\)
Mass of one suspended particle \(=m^{\prime}\)
Mass of the medium displaced \(=m\)
The volume of a suspended particle \(=V\)
According to Archimedes’ principle for a particle suspended in a liquid column, the effective weight of the suspended particle is given as:
Weight of the medium displaced – Weight of the suspended particle
\(
\begin{aligned}
& =m g-m^{\prime} g \\
& =m g-V \rho^{\prime} g=m g-\left(\frac{m}{\rho}\right) \rho^{\prime} g \\
& =m g\left(1-\frac{\rho^{\prime}}{\rho}\right) \ldots \text {..(ii) }
\end{aligned}
\)
Gas constant, \(R=k_B N\)
\(
k_B=\frac{R}{N} \dots(iii)
\)
Substituting equation (ii) in place of \(m g\) in equation (i) and then using equation (iii), we get:
\(
\begin{aligned}
& \mathrm{n}_2=\mathrm{n}_1 \exp \left[-\mathrm{mg}\left(\mathrm{h}_2-\mathrm{h}_1\right) / \mathrm{k}_{\mathrm{B}} T\right] \\
& =n_1 \exp \left[\frac{-m g\left(h_2-h_1\right)}{k_B T}\right] \\
& =n_1 \exp \left[-m g(\rho-\rho \prime)\left(h_2-h_1\right) \frac{N}{R T \rho}\right]
\end{aligned}
\)

Example 5: Explain why (a) there is no atmosphere on the moon. (b) there is a fall in temperature with altitude.

Solution:

(a) The escape velocity of the moon is less than the root mean square velocity of the moon. Hence, the molecules of gas escape from the surface of the moon. The moon doesn’t have an atmosphere because the magnetic field is weak on the surface of the moon. Since the surface of the moon doesn’t absorb a measurable quantity of radiation the gas molecules are lost into space. The surroundings of the moon are vacuum. But in the case of our planet, it has more mass and a strong magnetic field. So that the earth has an atmosphere. Whereas, the moon has no atmosphere.
(b) Temperature generally decreases with an increase in altitude. This is because of the low pressure in that area, and the temperature decreases. Temperature and pressure are interrelated. Usually in the troposphere temperature decreases. The gases in the troposphere absorb radiation and thereby decrease the temperature. Pressure also decreases with height. Pressure at some point is the mass of the atmosphere. The other factors influencing the temperature are latitude, altitude, distance from the sea, humidity, etc.
Note:
(a) The moon doesn’t have an atmosphere because the magnetic field is weak on the surface of the moon. Since the surface of the moon doesn’t absorb a measurable quantity of radiation the gas molecules are lost into space.
(b)Temperature generally decreases with an increase in altitude. Usually in the troposphere temperature decreases. The gases in the troposphere absorb radiation and thereby decrease the temperature.

Example 6: Consider an ideal gas with the following distribution of speeds.

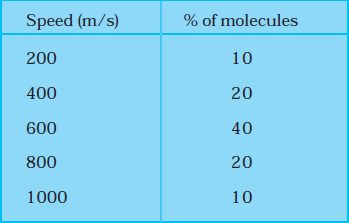
(i) Calculate \(V_{\mathrm{rms}}\) and hence T. \(\left(m=3.0 \times 10^{-26} \mathrm{~kg}\right)\)
(ii) If all the molecules with speed \(1000 \mathrm{~m} / \mathrm{s}\) escape from the system, calculate new \(V_{r m s}\) and hence \(T\).

Solution:

(i)

\(
\begin{aligned}
& V_{r m s}^2=\frac{\sum n_i v_i^2}{\sum n_i} \\
& =\frac{10 \times(200)^2+20 \times(400)^2+40 \times(600)^2+20 \times(800)^2+10 \times(1000)^2}{100} \\
& =\frac{10 \times 100^2 \times(1 \times 4+2 \times 16+4 \times 36+2 \times 64+1 \times 100)}{100} \\
& =1000 \times(4+32+144+128+100)=408 \times 1000 \mathrm{~m}^2 / \mathrm{s}^2 \\
& \therefore v_{r m s}=639 \mathrm{~m} / \mathrm{s} \\
& \frac{1}{2} m v_{r m s}^2=\frac{3}{2} \mathrm{kT} \\
& \therefore T=\frac{1}{3} \frac{\mathrm{mv}_{r \mathrm{~ms}}^2}{\mathrm{k}}=\frac{1}{3} \times \frac{3.0 \times 10^{-26} \times 4.08 \times 10^5}{1.38 \times 10^{-23}} \\
& \quad=2.96 \times 10^2 \mathrm{~K}=296 \mathrm{~K}
\end{aligned}
\)

(ii) 

\(
\begin{aligned}
V_{r m s}^2= & \frac{10 \times(200)^2+20 \times(400)^2+40 \times(600)^2+20 \times(800)^2}{90} \\
& =\frac{10 \times 100^2 \times(1 \times 4+2 \times 16+4 \times 36+2 \times 64)}{90} \\
& =10000 \times \frac{308}{9}=342 \times 1000 \mathrm{~m}^2 / \mathrm{s}^2 \\
v_{\mathrm{rms}} & =584 \mathrm{~m} / \mathrm{s} \\
T & =\frac{1}{3} \frac{\mathrm{mV}_{\mathrm{rms}}^2}{\mathrm{k}}=248 \mathrm{~K}
\end{aligned}
\)

Example 7: Ten small planes are flying at a speed of \(150 \mathrm{~km} / \mathrm{h}\) in total darkness in an air space that is \(20 \times 20 \times 1.5 \mathrm{~km}^3\) in volume. You are in one of the planes, flying at random within this space with no way of knowing where the other planes are. On average about how long a time will elapse between near collision with your plane. Assume for this rough computation that a safety region around the plane can be approximated by a sphere of radius \(10 \mathrm{~m}\).

Solution:

We can consider the planes as the motion of molecules in confined space. The distance between the two planes travelled between the collision or just to avoid an accident is the time of relaxation for the mean free path \(\lambda\).
\(
\begin{aligned}
& \text { Time }=\frac{\text { Distance }}{\text { Speed }} \\
& =\frac{\lambda}{v} \\
& =\frac{1}{\sqrt{2} n \cdot \pi d^2 \cdot v} \\
& \mathrm{~N}=\text { number of particles per unit volume } \mathrm{V}=\frac{\mathrm{N}}{\text { Volume }} \\
& n=\frac{10}{20 \times 20 \times 1.5 \mathrm{Km}^3} \\
& =0.0167 \mathrm{~km}^{-3} \\
& d=2 \times 10 \mathrm{~m}^{-3} \\
& =20 \mathrm{~m} \\
& =20 \times 10^{-3} \mathrm{~km}, v=150 \mathrm{kmh}^{-1} \\
& \therefore \text { Time }=\frac{1}{\sqrt{2} n \pi d^2 v}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{1.414 \times 0.0167 \times 3.14 \times 20 \times 20 \times 10^{-6} \times 150} \\
& t=\frac{10^6}{4448.8} \\
& =255 \mathrm{hrs}
\end{aligned}
\)

Example 8: A box of \(1.00 \mathrm{~m}^3\) is fllled with nitrogen at \(1.50 \mathrm{~atm}\) at \(300 \mathrm{~K}\). The box has a hole of an area \(0.010 \mathrm{~mm}^2\). How much time is required for the pressure to reduce by \(0.10 \mathrm{~atm}\), if the pressure outside is 1 atm.

Solution:

\(V_{1 x}=\) speed of molecule inside the box along \(x\) direction \(n_1=\) number of molecules per unit volume In time \(\Delta t\), particles moving along the wall will collide if they are within \(V_{1 x} \Delta\) t distance. Let \(a=\) area of the wall.
No. of particles colliding in time \(\Delta \mathrm{t}=\) \((1 / 2) n_t\left(V_{t x} \Delta t\right)\) a (factor of \(1 / 2\) due to motion towards wall):
In general, gas is in equilibrium as the wall is very large as compared to hole.
\(
\begin{aligned}
& \therefore V_{1 x}^2+V_{1 y}^2+V_{1 z}^2=V_{r m s}^2 \\
& \therefore V_{1 x}^2=\frac{V_{r m s}^2}{3} \\
& \frac{1}{2} m V_{r m s}^2=\frac{3}{2} k T \Rightarrow V_{r m s}^2=\frac{3 k T}{m} \\
& \therefore V_{1 x}^2=\frac{k T}{m}
\end{aligned}
\)
No. of particles colliding in time \(\Delta t=(1 / 2) n_1 \sqrt{ }(\mathrm{kT} / \mathrm{m}) \Delta t\) a. If particles collide along a hole, they move out. Similarly, outer particles colliding along the hole will move in.

Net particle flow in time \(\Delta t=1 / 2\left(n_1-n_2\right) \sqrt{ }(\mathrm{kT} / \mathrm{m}) \Delta t\) a as temperature is same in and out
\(
\begin{aligned}
& p V=\mu R T \Rightarrow \mu=P V \\
& n=\frac{\mu N_A}{V}=\frac{P N_A}{R T}
\end{aligned}
\)
After some time \(\tau\) pressure changes to \(p_1^{\prime}\) inside
\(
\therefore n_1^{\prime}=\frac{P_1^{\prime} N_A}{R T}
\)
\(
\begin{aligned}
& n_1 V-n_1^{\prime} V=\text { no. of particle gone out }=\frac{1}{2}\left(n_1-n_2\right) \sqrt{\frac{k T}{m}} \tau a \\
& \therefore \frac{P_1 N_A}{R T} V-\frac{P_1^{\prime} N_A}{R T} V=\frac{1}{2}\left(P_1-P_2\right) \frac{N_A}{R T} \sqrt{\frac{k T}{m}} \tau a \\
& \therefore \tau=2\left(\frac{P_1-P_1^{\prime}}{P_1-P_2}\right) \frac{V}{a} \sqrt{\frac{m}{k T}} \\
& =2\left(\frac{1.5-1.4}{1.5-1.0}\right) \frac{5 \times 1.00}{0.01 \times 10^{-6}} \sqrt{\frac{46.7 \times 10^{-27}}{1.38 \times 10^{-23} \times 300}} \\
& =1.38 \times 10^5 \mathrm{~s}
\end{aligned}
\)

Example 9: Consider a rectangular block of wood moving with a velocity \(v_0\) in a gas at temperature Tand mass density \(\rho\). Assume the velocity is along \(x\)-axis and the area of cross-section of the block perpendicular to \(v_0\) is \(\mathrm{A}\). Show that the drag force on the block is \(4 \rho A v_0 \sqrt{\frac{k T}{m}}\), where \(m\) is the mass of the gas molecule.

Solution:

Using the kinetic theory of ideal gases,
\(\mathrm{n}=\) number density of molecules
\(\mathrm{m}=\) mass of each gas molecule
\(v_{R M S}=\) RMS velocity of each gas molecule
\(v=\) velocity of molecule that is moving along \(x\)-axis
As RMS velocity along each direction is equal \(\left[\left(v_{R M S}\right)_x=\left(v_{R M S}\right)_Y=\left(v_{R M S}\right)_Z=v\right]\)
Now, \(v_{R M S}^2=\left(v_{R M S}\right)_x^2=\left(v_{R M S}\right)_y^2=\left(v_{R M S}\right)_z^2=3 v^2\)
\(\Rightarrow v^2=\frac{v_{R M S}^2}{3}\)
Let the block move toward the right. It faces “front” molecules that collide with the block while moving towards the left. Also, there are “back” molecules that collide with the block from behind while moving towards the right.
The relative speed of “front” molecules before collision \(=v+v_0\)
The relative speed of “back” molecules before collision \(=v-v_0\)
Since collisions are elastic, the relative speed of molecules remains the same before and after the collision. Since, the block is heavy, so it does not change its speed and direction of motion.
After the collision, “front” molecules move towards the right, and “back” molecules move towards the left.
Let \(v_1\) and \(v_2\) be the speeds of “front” and “back” molecules along \(x\)-axis respectively after the collision.
So, \(v+v_0=v_1-v_0 \Rightarrow v_1=v+2 v_0\)
And, \(v-v_0=v_0-\left(-v_2\right) \Rightarrow v_2=v-2 v_0\)
The magnitude of momentum transferred by each “front” molecule to the block =
\((\) mass of molecule \()(\) change in its velocity \()=m\left|\left\{\left(v+2 v_0\right)-(-v)\right\}\right|=2 m\left(v+v_0\right)\)
Its direction is towards the left.
The magnitude of momentum transferred by each “back” molecule to the block =
\((\) mass of molecule \()(\) change in its velocity \()=m\left|\left\{-\left(v-2 v_0\right)-(v)\right\}\right|=2 m\left(v-v_0\right)\)
Its direction is towards the right.
Consider an interval of time \(\Delta t\). All “front” molecules within a distance (along \(\mathrm{x}\)-axis) \(\left(v+v_0\right) \Delta t\) will collide with the block. And “back”
molecules within a distance (along \(\mathrm{x}\)-axis) \(\left(v-v_0\right) \Delta t\) will collide with the block.
The momentum transferred by “front” molecules in time \(\Delta t=\)
[half the number of molecules in volume \(\left.A\left(v+v_0\right) \Delta t\right](\) momentum transferred by each “front” molecule)
\(
\left[\frac{1}{2} n A\left(v+v_0\right) \Delta t\right]\left(2 m\left(v+v_0\right)\right)=n m A\left(v+v_0\right)^2 \Delta t
\)
(The factor of half is considered because half of the molecules move towards the block and other half towards the block, in each direction).
Similarly, momentum transferred by “back” molecules in time \(\Delta t=\)
[half the number of molecules in volume \(A\left(v-v_0\right) \Delta t\) ] (momentum transferred by each “back” molecule)
\(
\left[\frac{1}{2} n A\left(v-v_0\right) \Delta t\right]\left(2 m\left(v-v_0\right)\right)=n m A\left(v-v_0\right)^2 \Delta t
\)
Total momentum transferred to the block in time \(\Delta t\) is \(=n m A\left(v+v_0\right)^2 \Delta t-n m A\left(v-v_0\right)^2 \Delta t\) \(=4 n m A v v_0 \Delta t\)
Hence, drag force on the block \(=\frac{\text { momentum transferred to block }}{\text { time }}=4 n m A v v_0\)
But \(m n=\rho\) (density of gas)
And \(v_{R M S}=\sqrt{\frac{3 k T}{m}}\)
So, \(v^2=\frac{v_{R M S}^2}{3}=\frac{\frac{3 k T}{m}}{3}=\frac{k T}{m}\)
Hence, drag force \(=4 \rho A v_0 \sqrt{\frac{k T}{m}}\).