Sample Exercises
Quiz Summary
0 of 39 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 39 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 39
1. Question
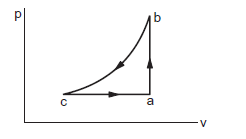
A sample of an ideal gas is taken through the cyclic process abca figure below. It absorbs \(50 \mathrm{~J}\) of heat during the part ab, no heat during bc and rejects \(70 \mathrm{~J}\) of heat during ca. \(40 \mathrm{~J}\) of work is done on the gas during the part bc. (a) Find the internal energy of the gas at b and \(c\) if it is \(1500 \mathrm{~J}\) at a. (b) Calculate the work done by the gas during the part ca.
CorrectIncorrectHint
(a) In the part \(a b\) the volume remains constant. Thus, the work done by the gas is zero. The heat absorbed by the gas is \(50 \mathrm{~J}\). The increase in internal energy from \(a\) to \(b\) is
\(
\Delta U=\Delta Q=50 \mathrm{~J}
\)
As the internal energy is \(1500 \mathrm{~J}\) at \(a\), it will be \(1550 \mathrm{~J}\) at \(b\). In the part \(b c\), the work done by the gas is \(\Delta W=-40 \mathrm{~J}\) and no heat is given to the system. The increase in internal energy from \(b\) to \(c\) is
\(
\Delta U=-\Delta W=40 \mathrm{~J}
\)
As the internal energy is \(1550 \mathrm{~J}\) at \(b\), it will be \(1590 \mathrm{~J}\) at \(c\).
(b) The change in internal energy from \(c\) to \(a\) is
\(
\Delta U=1500 \mathrm{~J}-1590 \mathrm{~J}=-90 \mathrm{~J}
\)
The heat given to the system is \(\Delta Q=-70 \mathrm{~J}\).
\(
\text { Using } \begin{aligned}
\Delta Q & =\Delta U+\Delta W \\
\Delta W & =\Delta Q-\Delta U \\
& =-70 \mathrm{~J}+90 \mathrm{~J}=20 \mathrm{~J}
\end{aligned}
\) -
Question 2 of 39
2. Question
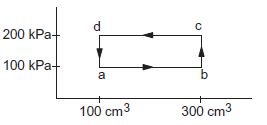
A thermodynamic system is taken through the cycle abcda (figure below). (a) Calculate the work done by the gas during the parts ab, bc, cd, and da. (b) Find the total heat rejected by the gas during the process.
CorrectIncorrectHint
(a) The work done during the part \(a b\),
\(
\begin{aligned}
& =\int_a^b p d V=(100 \mathrm{kPa}) \int_a^b d V \\
& =(100 \mathrm{kPa})\left(300 \mathrm{~cm}^3-100 \mathrm{~cm}^3\right)
\end{aligned}
\)
\(
=20 \mathrm{~J} \text {. }
\)
The work done during \(b c\) is zero as the volume does not change. The work done during \(c d\)
\(
\begin{aligned}
& =\int_c^d p d V=(200 \mathrm{kPa})\left(100 \mathrm{~cm}^3-300 \mathrm{~cm}^3\right) \\
& =-40 \mathrm{~J} .
\end{aligned}
\)
The work done during \(d a\) is zero as the volume does not change.
(b) The total work done by the system during the cycle \(a b c d a\)
\(
\Delta W=20 \mathrm{~J}-40 \mathrm{~J}=-20 \mathrm{~J} \text {. }
\)
The change in internal energy \(\Delta U=0\) as the initial state is the same as the final state. Thus \(\Delta Q=\Delta U+\Delta W=-20 \mathrm{~J}\). So the system rejects \(20 \mathrm{~J}\) of heat during the cycle. -
Question 3 of 39
3. Question
Calculate the increase in internal energy of \(1 \mathrm{~kg}\) of water at \(100^{\circ} \mathrm{C}\) when it is converted into steam at the same temperature and at 1 atm \((100 \mathrm{kPa})\). The density of water and steam are \(1000 \mathrm{~kg} \mathrm{~m}^{-3}\) and \(0.6 \mathrm{~kg} \mathrm{~m}^{-3}\) respectively. The latent heat of vaporization of water \(=2.25 \times 10^6 \mathrm{~J} \mathrm{~kg}^{-1}\)
CorrectIncorrectHint
The volume of \(1 \mathrm{~kg}\) of water
\(
=\frac{1}{1000} \mathrm{~m}^3 \text { and of } 1 \mathrm{~kg} \text { of steam }=\frac{1}{0 \cdot 6} \mathrm{~m}^3 \text {. }
\)
The increase in volume
\(
\begin{aligned}
& =\frac{1}{0.6} \mathrm{~m}^3-\frac{1}{1000} \mathrm{~m}^3 \\
& =(1.7-0.001) \mathrm{m}^3 \approx 1.7 \mathrm{~m}^3 .
\end{aligned}
\)
The work done by the system is \(p \Delta V\)
\(
\begin{aligned}
& =(100 \mathrm{kPa})\left(1.7 \mathrm{~m}^3\right) \\
& =1.7 \times 10^5 \mathrm{~J} .
\end{aligned}
\)
The heat given to convert \(1 \mathrm{~kg}\) of water into steam
\(
=2.25 \times 10^6 \mathrm{~J} \text {. }
\)
The change in internal energy is
\(
\begin{aligned}
\Delta U & =\Delta Q-\Delta W \\
& =2.25 \times 10^6 \mathrm{~J}-1.7 \times 10^5 \mathrm{~J} \\
& =2.08 \times 10^6 \mathrm{~J} .
\end{aligned}
\) -
Question 4 of 39
4. Question
The internal energy of a monatomic ideal gas is \(1.5 \mathrm{nRT}\). One mole of helium is kept in a cylinder of cross section \(8.5 \mathrm{~cm}^2\). The cylinder is closed by a light frictionless piston. The gas is heated slowly in a process during which a total of \(42 \mathrm{~J}\) heat is given to the gas. If the temperature rises through \(2^{\circ} \mathrm{C}\), find the distance moved by the piston. Atmospheric pressure \(=100 \mathrm{kPa}\).
CorrectIncorrectHint
The change in internal energy of the gas is
\(
\begin{aligned}
\Delta U & =1.5 n R(\Delta T) \\
& =1.5(1 \mathrm{~mol})\left(8.3 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right)(2 \mathrm{~K}) \\
& =24.9 \mathrm{~J}
\end{aligned}
\)
The heat given to the gas \(=42 \mathrm{~J}\).
The work done by the gas is
\(
\begin{aligned}
\Delta W & =\Delta Q-\Delta U \\
& =42 \mathrm{~J}-24 \cdot 9 \mathrm{~J}=17 \cdot 1 \mathrm{~J} .
\end{aligned}
\)
If the distance moved by the piston is \(x\), the work done is
\(
\Delta W=(100 \mathrm{kPa})\left(8.5 \mathrm{~cm}^2\right) x
\)
Thus,
or,
\(
\begin{gathered}
\left(10^5 \mathrm{~N} \mathrm{~m}^{-2}\right)\left(8.5 \times 10^{-4} \mathrm{~m}^{-2}\right) x=17.1 \mathrm{~J} \\
x=0.2 \mathrm{~m}=20 \mathrm{~cm} .
\end{gathered}
\) -
Question 5 of 39
5. Question
A steam engine intakes \(100 \mathrm{~g}\) of steam at \(100^{\circ} \mathrm{C}\) per minute and cools it down to \(20^{\circ} \mathrm{C}\). Calculate the heat rejected by the steam engine per minute. Latent heat of vaporization of steam \(=540 \mathrm{cal} \mathrm{g}^{-1}\).
CorrectIncorrectHint
Heat rejected during the condensation of steam in one minute
\(
=(100 \mathrm{~g}) \times\left(540 \mathrm{cal} \mathrm{g}^{-1}\right)=5.4 \times 10^4 \mathrm{cal} .
\)
Heat rejected during the cooling of water
\(
\begin{aligned}
& =(100 \mathrm{~g}) \times\left(1 \mathrm{cal} \mathrm{g}^{-1}{ }^{\circ} \mathrm{C}^{-1}\right)\left(100^{\circ} \mathrm{C}-20^{\circ} \mathrm{C}\right) \\
& =8000 \mathrm{cal} .
\end{aligned}
\)
Thus, heat rejected by the engine per minute
\(
\begin{aligned}
& =5.4 \times 10^4 \mathrm{cal}+0.8 \times 10^4 \mathrm{cal} \\
& =6.2 \times 10^4 \mathrm{cal} .
\end{aligned}
\) -
Question 6 of 39
6. Question
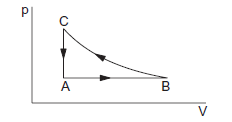
Figure shows a process ABCA performed on an ideal gas. Find the net heat given to the system during the process.
CorrectIncorrectHint
As the process is cyclic, the change in internal energy is zero. The heat given to the system is then equal to the work done by it.
The work done in part \(A B\) is \(W_1=0\) as the volume remains constant. The part \(B C\) represents an isothermal process so that the work done by the gas during this part is
\(
W_2=n R T_2 \ln \left(V_2 / V_1\right)
\)
During the part \(C A\),
\(
V \propto T
\)
So, \(V / T\) is constant and hence,
\(
p=\frac{n R T}{V} \text { is constant }
\)
The work done by the gas during the part \(C A\) is
\(
\begin{aligned}
W_3 & =p\left(V_1-V_2\right) \\
& =n R T_1-n R T_2 \\
& =-n R\left(T_2-T_1\right) .
\end{aligned}
\)
The net work done by the gas in the process \(A B C A\) is
\(
W=W_1+W_2+W_3=n R\left[T_2 \ln \frac{V_2}{V_1}-\left(T_2-T_1\right)\right] .
\)
The same amount of heat is given to the gas. -
Question 7 of 39
7. Question
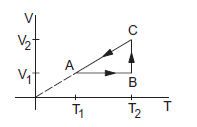
Consider the cyclic process \(A B C A\) on a sample of \(2.0 \mathrm{~mol}\) of an ideal gas as shown in figure below. The temperatures of the gas at \(A\) and \(B\) are \(300 \mathrm{~K}\) and \(500 \mathrm{~K}\) respectively. A total of \(1200 \mathrm{~J}\) heat is withdrawn from the sample in the process. Find the work done by the gas in part BC. Take \(R=8.3 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\).
CorrectIncorrectHint
The change in internal energy during the cyclic process is zero. Hence, the heat supplied to the gas is equal to the work done by it. Hence,
\(
W_{A B}+W_{B C}+W_{C A}=-1200 \mathrm{~J} \dots(i)
\)
The work done during the process \(A B\) is
\(
\begin{aligned}
W_{A B} & =p_A\left(V_B-V_A\right) \\
& =n R\left(T_B-T_A\right) \\
& =(2.0 \mathrm{~mol})\left(8.3 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right)(200 \mathrm{~K}) \\
& =3320 \mathrm{~J} .
\end{aligned}
\)
The work done by the gas during the process \(C A\) is zero as the volume remains constant. From (i),
or,
\(
\begin{aligned}
3320 \mathrm{~J}+W_{B C} & =-1200 \mathrm{~J} \\
W_{B C} & =-4520 \mathrm{~J} . \\
& \approx-4500 \mathrm{~J} .
\end{aligned}
\) -
Question 8 of 39
8. Question
\(2.00 \mathrm{~mol}\) of a monatomic ideal gas \((U=1.5 \mathrm{nRT})\) is enclosed in an adiabatic, fixed, vertical cylinder fitted with a smooth, light adiabatic piston. The piston is connected to a vertical spring of spring constant \(200 \mathrm{~N} \mathrm{~m}^{-1}\) as shown in figure below. The area of cross section of the cylinder is \(20.0 \mathrm{~cm}^2\). Initially, the spring is at its natural length and the temperature of the gas is \(300 \mathrm{~K}\). The atmospheric pressure is \(100 \mathrm{kPa}\). The gas is heated slowly for some time by means of an electric heater so as to move the piston up through \(10 \mathrm{~cm}\). Find (a) the work done by the gas (b) the final temperature of the gas and (c) the heat supplied by the heater.
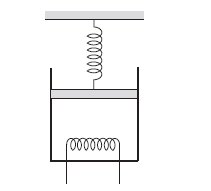CorrectIncorrectHint
(a) The force by the gas on the piston is
\(
F=p_0 A+k x
\)
where \(p_0=100 \mathrm{kPa}\) is the atmospheric pressure, \(A=20 \mathrm{~cm}^2\) is the area of cross section, \(k=200 \mathrm{~N} \mathrm{~m}^{-1}\) is the spring constant and \(x\) is the compression of the spring. The work done by the gas as the piston moves through \(l=10 \mathrm{~cm}\) is
\(
\begin{aligned}
W= & \int_0^l F d x \\
= & p_0 A l+\frac{1}{2} k l^2 \\
= & \left(100 \times 10^3 \mathrm{~Pa}\right) \times\left(20 \times 10^{-4} \mathrm{~m}^2\right) \times\left(10 \times 10^{-2} \mathrm{~m}\right) \\
& \quad+\frac{1}{2}\left(200 \mathrm{~N} \mathrm{~m}^{-1}\right) \times\left(100 \times 10^{-4} \mathrm{~m}^2\right) \\
= & 20 \mathrm{~J}+1 \mathrm{~J}=21 \mathrm{~J} .
\end{aligned}
\)
(b) The initial temperature is \(T_1=300 \mathrm{~K}\). Let the final temperature be \(T_2\). We have
\(
\begin{aligned}
& n R T_1=p_0 V_0 \\
& \text { and } n R T_2=p V_2=\left(p_0+\frac{k l}{A}\right)\left(V_0+A l\right) \\
& =n R T_1+p_0 A l+k l^2+\frac{k l n R T_1}{A p_0} \\
& \text { or, } \quad T_2=T_1+\frac{p_0 A l+k l^2}{n R}+\frac{k l T_1}{A p_0} \\
& =(300 \mathrm{~K})+\frac{20 \mathrm{~J}+2 \mathrm{~J}}{(2 \cdot 0 \mathrm{~mol})\left(8 \cdot 3 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right)} \\
& +\frac{\left(200 \mathrm{~N} \mathrm{~m}^{-1}\right) \times\left(10 \times 10^{-2} \mathrm{~m}\right) \times(300 \mathrm{~K})}{\left(20 \times 10^{-4} \mathrm{~m}^2\right) \times\left(100 \times 10^3 \mathrm{~Pa}\right)} \\
& =300 \mathrm{~K}+1 \cdot 325 \mathrm{~K}+30 \mathrm{~K} \\
& \approx 331 \mathrm{~K} \text {. } \\
&
\end{aligned}
\)
(c) The internal energy is \(U=1.5 \mathrm{nRT}\).
The change in internal energy is
\(
\begin{aligned}
\Delta U & =1.5 \mathrm{nR} \Delta T \\
& =1.5 \times(2.00 \mathrm{~mol}) \times\left(8.3 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right) \times(31 \mathrm{~K}) \\
& =772 \mathrm{~J} .
\end{aligned}
\)
From the first law,
\(
\begin{aligned}
\Delta Q & =\Delta U+\Delta W \\
& =772 \mathrm{~J}+21 \mathrm{~J}=793 \mathrm{~J}
\end{aligned}
\) -
Question 9 of 39
9. Question
A sample of an ideal gas has pressure \(p_0\), volume \(V_0\) and temperature \(T_0\). It is isothermally expanded to twice its original volume. It is then compressed at constant pressure to have the original volume \(V_0\). Finally, the gas is heated at constant volume to get the original temperature. Show the process in a \(V-T\) diagram. Calculate the heat absorbed in the process.
CorrectIncorrectHint
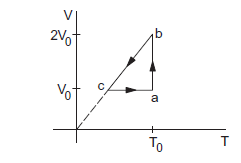
(a) The \(V-T\) diagram for the process is shown in figure below. The initial state is represented by the point \(a\). In the first step, it is isothermally expanded to a volume \(2 V_0\). This is shown by \(a b\). Then the pressure is kept constant and the gas is compressed to the volume \(V_0\). From the ideal gas equation, VIT is constant at constant pressure. Hence, the process is shown by a line \(b c\) which passes through the origin. At point \(c\), the volume is \(V_0\). In the final step, the gas is heated at constant volume to a temperature \(T_0\). This is shown by \(c a\). The final state is the same as the inital state.
(b) The process is cyclic so that the change in internal energy is zero. The heat supplied is, therefore, equal to the work done by the gas. The work done during \(a b\) is
\(
W_1=n R T_0 \ln \frac{2 V_0}{V_0}=n R T_0 \ln 2=p_0 V_0 \ln 2 .
\)
Also from the ideal gas equation,
or,
\(
\begin{aligned}
p_a V_a & =p_b V_b \\
p_b & =\frac{p_a V_a}{V_b}=\frac{p_0 V_0}{2 V_0}=\frac{p_0}{2} .
\end{aligned}
\)
In the step \(b c\), the pressure remains constant. Hence, the work done is,
\(
W_2=\frac{p_0}{2}\left(V_0-2 V_0\right)=-\frac{p_0 V_0}{2} .
\)
In the step \(c a\), the volume remains constant and so the work done is zero. The net work done by the gas in the cyclic process is
\(
\begin{aligned}
W & =W_1+W_2 \\
& =p_0 V_0[\ln 2-0.5] \\
& =0.193 p_0 V_0 .
\end{aligned}
\)
Hence, the heat supplied to the gas is \(0.193 p_0 V_0\). -
Question 10 of 39
10. Question
A sample of \(100 \mathrm{~g}\) water is slowly heated from \(27^{\circ} \mathrm{C}\) to \(87^{\circ} \mathrm{C}\). Calculate the change in the entropy of the water.
Specific heat capacity of water \(=4200 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\).CorrectIncorrect -
Question 11 of 39
11. Question
A heat engine operates between a cold reservoir at temperature \(T_2=300 \mathrm{~K}\) and \(a\) hot reservoir at temperature \(T_1\). It takes \(200 \mathrm{~J}\) of heat from the hot reservoir and delivers \(120 \mathrm{~J}\) of heat to the cold reservoir in a cycle. What could be the minimum temperature of the hot reservoir?
CorrectIncorrectHint
The work done by the engine in a cycle is
\(
W=200 \mathrm{~J}-120 \mathrm{~J}=80 \mathrm{~J} \text {. }
\)
The efficiency of the engine is
\(
\eta=\frac{W}{Q}=\frac{80 \mathrm{~J}}{200 \mathrm{~J}}=0 \cdot 40 .
\)
From Carnot’s theorem, no engine can have an efficiency greater than that of a Carnot engine.
Thus, \(\quad 0 \cdot 40 \leq 1-\frac{T_2}{T_1}=1-\frac{300 \mathrm{~K}}{T_1}\) or, or, or, \(\quad T_1 \geq 500 \mathrm{~K}\).
The minimum temperature of the hot reservoir has to be \(500 \mathrm{~K}\). -
Question 12 of 39
12. Question
A thermally insulated, closed copper vessel contains water at \(15^{\circ} \mathrm{C}\). When the vessel is shaken vigorously for 15 minutes, the temperature rises to \(17^{\circ} \mathrm{C}\). The mass of the vessel is \(100 \mathrm{~g}\) and that of the water is \(200 \mathrm{~g}\). The specific heat capacities of copper and water are \(420 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\) and \(4200 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\) respectively. Neglect any thermal expansion. (a) How much heat is transferred to the liquid-vessel system? (b) How much work has been done on this system? (c) How much is the increase in the internal energy of the system?
CorrectIncorrectHint
Given:-
The system comprises of an insulated copper vessel that contains water.
\(
t_1=15^{\circ} \mathrm{C}, t_2=17^{\circ} \mathrm{C}
\)
\(t_1\) is the initial temperature of the system
\(t_2\) is the final temperature of the system
\(\Delta t=\) Change in the temperature of the system \(=t_2-t_1\)
\(
=17^{\circ} \mathrm{C}-15^{\circ} \mathrm{C}=2^{\circ} \mathrm{C}=275 \mathrm{~K}
\)
Mass of the vessel, \(\mathrm{m}_{\mathrm{v}}=100 \mathrm{~g}=0.1 \mathrm{~kg}\)
Mass of water, \(\mathrm{m}_{\mathrm{w}}=200 \mathrm{~g}=0.2 \mathrm{~kg}\)
Specific heat capacity of copper, \(c_{\mathrm{u}}=420 \mathrm{~J} / \mathrm{kg}-\mathrm{K}\)
Specific heat capacity of water, \(c_w=4200 \mathrm{~J} / \mathrm{kg}-\mathrm{K}\)
(a) Since the system is insulated from the surroundings, no heat is transferred between the system and the surroundings. This implies that the heat transferred to the liquid vessel system is zero. The internal heat is shared between the vessel and water.
(b) Work done on the system
\(
\begin{aligned}
& =m_w c_w \Delta t+m_v c_u \Delta t \\
& \Rightarrow \mathrm{dW}=100 \times 10^{-3} \times 420 \times 2+200 \times 10^{-3} \times 4200 \times 2 \\
& \Rightarrow \mathrm{dW}=84+84 \times 20=84 \times 21 \\
& \Rightarrow \mathrm{dW}=1764 \mathrm{~J}
\end{aligned}
\)
(c) Using the first law of thermodynamics, we get
\(
d Q=d W+d U
\)
Here, \(d W=p d V\)
Work is done by the system. Thus, work done is negative.
\(
\begin{aligned}
& \Rightarrow \mathrm{dQ}=0 \quad \ldots . . . \ldots . . .(\text { given) } \\
& \mathrm{dU}=-\mathrm{dW} \\
& =-(-1764)=1764 \mathrm{~J} \text { [since } d W=-v e \text { work done on the system] }
\end{aligned}
\) -
Question 13 of 39
13. Question
The figure below shows a paddle wheel coupled to a mass of \(12 \mathrm{~kg}\) through fixed frictionless pulleys. The paddle is immersed in a liquid of heat capacity \(4200 \mathrm{~J} \mathrm{~K}^{-1}\) kept in an adiabatic container. Consider a time interval in which the \(12 \mathrm{~kg}\) block falls slowly through \(70 \mathrm{~cm}\). (a) How much heat is given to the liquid? (b) How much work is done on the liquid? (c) Calculate the rise in the temperature of the liquid neglecting the heat capacity of the container and the paddle.
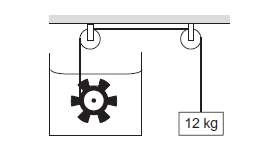CorrectIncorrectHint
(a) Heat transfer does not take place but work is done which is then converted into heat. Thus, heat given to liquid \(\mathrm{Q}=0\)
(b) Work done on liquid,
\(
\begin{aligned}
& W=P . E=\text { mgh } \\
& =12 \times 10 \times 0.70 \\
& =84 \mathrm{~J}
\end{aligned}
\)
(c) We know
\(
\begin{aligned}
& W=m s \Delta t \\
& 84=1 \times 4200 \times \Delta t
\end{aligned}
\)
\(
\Delta t=0.02^{\circ} \mathrm{C}
\) -
Question 14 of 39
14. Question
A \(100 \mathrm{~kg}\) block is started with a speed of \(2.0 \mathrm{~m} \mathrm{~s}^{-1}\) on a long, rough belt kept fixed in a horizontal position. The coefficient of kinetic friction between the block and the belt is 0-20. (a) Calculate the change in the internal energy of the block-belt system as the block comes to a stop on the belt. (b) Consider the situation from a frame of reference moving at \(2.0 \mathrm{~m} \mathrm{~s}^{-1}\) along the initial velocity of the block. As seen from this frame, the block is gently put on a moving belt and in due time the block starts moving with the belt at \(2.0 \mathrm{~m} \mathrm{~s}^{-1}\). Calculate the increase in the kinetic energy of the block as it stops slipping past the belt. (c) Find the work done in this frame by the external force holding the belt.
CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{m}=100 \mathrm{~kg}, \mathrm{u}=2.0 \mathrm{~m} / \mathrm{s} \\
& \mathrm{v}=0, \mu \mathrm{k}=0.2
\end{aligned}
\)
a) Internal energy of the belt-block system will decrease when the block will lose its KE in heat due to friction.
Thus,
\(
\begin{aligned}
& \mathrm{KE} \text { lost }=\frac{1}{2} m u^2-\frac{1}{2} m \nu^2 \\
& \frac{1}{2} m\left(u^2-\nu^2\right) \\
& \frac{1}{2} \times 100 \times\left(2^2-0^2\right) \\
& =200 \mathrm{~J}
\end{aligned}
\)
b) Velocity of the frame is given by
\(
\begin{aligned}
& \mathrm{u}_f=2.0 \mathrm{~m} / \mathrm{s} \\
& u^{\prime}=u-u_f=2-2=0 \\
& v^{\prime}=0-2=-2 \mathrm{~m} / \mathrm{s} \\
& \mathrm{KE} \text { lost }=\frac{1}{2} m u^2-\frac{1}{2} m \nu t^2 \\
& =\frac{1}{2} m\left(0^2-\nu^2\right) \\
& =\frac{1}{2} \times 100 \times\left(0^2-2^2\right) \\
& =200 \mathrm{~J}
\end{aligned}
\)
C)
\(
\begin{aligned}
& f=\mu_k R \\
& \Rightarrow f=0.2 \times m g=0.2 \times 100 \times 10=200 \mathrm{~N} \\
& \text { Retardation }=\frac{f}{m}=\frac{200}{100}=2 \mathrm{~ms}^{-2}
\end{aligned}
\)
Distance moved by the block will be as seen from the frame=s
\(
\begin{aligned}
& v^{\prime 2}-u^2=2 a s \\
& \Rightarrow 2^2-0^2=2 \times 2 s \\
& \Rightarrow s=1 \mathrm{~m}
\end{aligned}
\)
Work done by the force responsible for accelarating as seen from the frame \(=f \mathrm{~s}\)
\(
=200 \times 1=200 \mathrm{~J}
\)
Work done by the belt to give it a final velocity of \(2 \mathrm{~m} / \mathrm{s}\)
\(
\begin{aligned}
& =\frac{1}{2} \mathrm{mv}^2 \\
& =\frac{1}{2} \times 100 \times(2)^2 \\
& =200 \mathrm{~J}
\end{aligned}
\)
Total work done by external force as seen from the frame \(200+200=400 \mathrm{~J}\) -
Question 15 of 39
15. Question
Calculate the change in internal energy of a gas kept in a rigid container when \(100 \mathrm{~J}\) of heat is supplied to it.
CorrectIncorrectHint
Heat supplied to the system,
\(
\Delta \mathrm{Q}=100 \mathrm{~J}
\)
Using the first law of thermodynamics, we get
\(
\Delta U=\Delta Q-\Delta W
\)
Since the container is rigid, initial volume of the system is equal to the final volume of the system. Thus,
\(
\begin{aligned}
& \Delta V=V_f-V_i=0 \\
& \Delta \mathrm{W}=\mathrm{P} \\
& \Delta \mathrm{V}=0 \\
& \Delta \mathrm{U}=\Delta \mathrm{Q}=100 \mathrm{~J}
\end{aligned}
\)
We see that heat supplied to the system is used up in raising the internal energy of the system. -
Question 16 of 39
16. Question
The pressure of a gas changes linearly with volume from \(10 \mathrm{kPa}, 200 \mathrm{cc}\) to \(50 \mathrm{kPa}, 50 \mathrm{cc}\). (a) Calculate the work done by the gas. (b) If no heat is supplied or extracted from the gas, what is the change in the internal energy of the gas?
CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{P}_1=10 \mathrm{kPa} \\
& =10 \times 10^3 \mathrm{~Pa} \\
& \mathrm{P}_2=50 \times 10^3 \mathrm{~Pa} \\
& \mathrm{~V}_1=200 \mathrm{CC}, \mathrm{V}_2=50 \mathrm{CC}
\end{aligned}
\)
(i) work done on the gas
\(
\begin{aligned}
& =\left[\left(\frac{1}{2}\right)(10+50) \times 10^3 \times(50-200) \times 10^{-6}\right] \\
& =-4.5 \mathrm{~J}
\end{aligned}
\)
(ii) \(\triangle Q=0\),
So, \(\Delta U=-\Delta W=4.5 \mathrm{~J}\) -
Question 17 of 39
17. Question
An ideal gas is taken from an initial state \(i\) to a final state \(f\) in such a way that the ratio of the pressure to the absolute temperature remains constant. What will be the work done by the gas?
CorrectIncorrectHint
Let
\(P_1=\) Initial pressure
\(P_2=\) Final pressure
\(\mathrm{T}_1=\) Absolute initial temperature
\(T_2=\) Absolute final temperature
Given:
\(
\frac{P_1}{T_1}=\frac{P_2}{T_2}
\)
Using the ideal gas equation, we get
\(
P V=n R T
\)
If \(\mathrm{n}\) is the number of moles of the gas and \(R\) is the universal gas constant, then
\(
\begin{aligned}
& \frac{P_1}{T_1}=\frac{n R}{V_1} \text { and } \frac{P_2}{T_2}=\frac{n R}{V_2} \\
& \Rightarrow V_1=V_2 \ldots \ldots\left[\because \frac{P_1}{T_1}=\frac{P_2}{T_2}\right] \\
& \Rightarrow \Delta V=V_2-V_1=0
\end{aligned}
\)
Thus, Work done by gas \(=P \Delta V=0\) -
Question 18 of 39
18. Question
The figure below shows three paths through which a gas can be taken from state A to state B. Calculate the work done by the gas in each of the three paths.
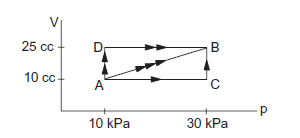CorrectIncorrectHint
\(
\text { In path } \mathrm{ACB} \text {, }
\)
\(
W_{A C}+W_{B C}=0+p d v=30 \times 10^3(25-10) \times 10^{-6}=0.45 \mathrm{~J}
\)
In path \(A B, W_{A B}=1 / 2 \times(10+30) \times 10^3 15 \times 10^{-6}=0.30 \mathrm{~J}\)
In path \(A D B, W=W_{A D}+W_{D B}=10 \times 10^3(25-10) \times 10^{-6}+0=0.15 \mathrm{~J}\) -
Question 19 of 39
19. Question
When a system is taken through the process \(a b c\) shown in the figure below, \(80 \mathrm{~J}\) of heat is absorbed by the system and \(30 \mathrm{~J}\) of work is done by it. If the system does \(10 \mathrm{~J}\) of work during the process \(a d c\), how much heat flows into it during the process?
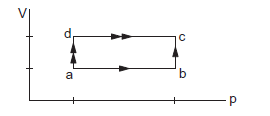CorrectIncorrectHint
\(
\Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W}
\)
In abc, \(\Delta Q=80 \mathrm{~J}, \Delta \mathrm{W}=30 \mathrm{~J}\)
So, \(\Delta U=(80-30) \mathrm{J}=50 \mathrm{~J}\)
Now in adc, \(\Delta \mathrm{W}=10 \mathrm{~J}\)
So, \(\Delta \mathrm{Q}=10+50=60 \mathrm{~J}[\therefore \Delta \mathrm{U}=50 \mathrm{~J}]\) -
Question 20 of 39
20. Question
\(50 \mathrm{cal}\) of heat should be supplied to take a system from the state \(A\) to the state \(B\) through the path \(A C B\) as shown in the figure below. Find the quantity of heat to be supplied to take it from \(A\) to \(B\) via \(A D B\).
CorrectIncorrectHint
process ACB:
\(
\begin{aligned}
& \Delta_{A C B}=\Delta W_{A C}+\Delta W_{C B} \\
& =50 \times 10^3 \times(400-200) \times 10^{-6}+0 \\
& =10 J=\frac{10}{4.2}=2.4 \mathrm{cal} \\
& \Delta Q=50 \mathrm{cal} \\
& \Delta Q=\Delta U+\Delta W=U_B-U_A+\Delta W \\
& 50=\left(U_B-U_A\right)+2.4 \\
& U_B-U_A=47.6 \mathrm{cal}
\end{aligned}
\)
Process ADB:
\(
\begin{aligned}
& \Delta W_{A D B}=\Delta W_{A D}+\Delta W_{D B} \\
& =0+155 \times 10^3 \times(400-200) \times 10^{-6} \\
& =31 J=\frac{31}{4.2}=7.4 \mathrm{cal} \\
& \Delta Q=\Delta U+\Delta W=U_B-U_A+7.4 \\
& =47.6+7.4 \\
& =55 \mathrm{cal}
\end{aligned}
\) -
Question 21 of 39
21. Question
Calculate the heat absorbed by a system in going through the cyclic process shown in the figure below.
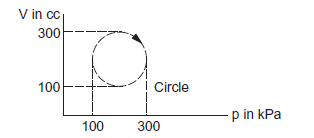CorrectIncorrectHint
Heat absorbed \(=\) Work done
= Area under the graph in the given case.
Heat absorbed \(=\) area of the circle
\(
\begin{aligned}
& =\pi \times 10^4 \times 10^{-6} \times 10^3 \mathrm{~J} \\
& =3.14 \times 10=31.4 \mathrm{~J}
\end{aligned}
\) -
Question 22 of 39
22. Question
A gas is taken through a cyclic process \(A B C A\) as shown in the figure below. If \(2 \cdot 4 \mathrm{cal}\) of heat is given in the process, what is the value of \(J\)?
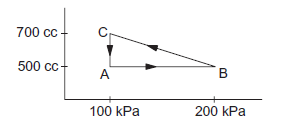CorrectIncorrectHint
\(
\begin{aligned}
& d Q=2.4 \mathrm{cal}=2.4 \mathrm{~J} \text { Joules } \\
& d W=W_{A B}+W_{B C}+W_{A C} \\
& =0+(1 / 2) \times(100+200) \times 10^3 200 \times 10^{-6}-100 \times 10^3 \times 200 \times 10^{-6} \\
& =(1 / 2) \times 300 \times 10^3 200 \times 10^{-6}-20=30-20=10 \text { joules. } \\
& d U=0(\text { in a cyclic process) } \\
& d Q=d U+d W \\
& \Rightarrow 2.4 \mathrm{~J}=10 \\
& \Rightarrow \mathbf{J}=10 / 2.4 \approx \mathbf{4 . 1 7} \mathrm{J} / \mathrm{Cal} .
\end{aligned}
\) -
Question 23 of 39
23. Question
A substance is taken through the process \(a b c\) as shown in the figure below. If the internal energy of the substance increases by \(5000 \mathrm{~J}\) and a heat of \(2625 \mathrm{cal}\) is given to the system, calculate the value of \(J\).
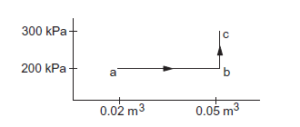CorrectIncorrectHint
\(
\begin{aligned}
& \text { Now, } \Delta Q=(2625 \times {J}) \mathrm{J} \\
& \Delta U=5000 \mathrm{~J}
\end{aligned}
\)
From Graph \(\Delta \mathrm{W}=200 \times 10^3 \times 0.03=6000 \mathrm{~J}\).
NoW, \(\Delta \mathrm{Q}=\Delta \mathrm{W}+\Delta \mathrm{U}\)
\(
\Rightarrow 2625 {J}=(6000+5000) \mathrm{~J}
\)
\(
\begin{aligned}
& {J}=11000 / 2625 \\
& =4.19 \mathrm{~J} / \mathrm{Cal}
\end{aligned}
\) -
Question 24 of 39
24. Question
A gas is taken along the path AB as shown in the figure below. If 70 cal of heat is extracted from the gas in the process calculate the change in the internal energy of the system.
CorrectIncorrectHint
Given: \(70 \mathrm{cal}\) of heat is extracted from the system.
Here,
\(
\Delta \mathrm{Q}=-70 \mathrm{cal}=-(70 \times 4.2) \mathrm{J}=-294 \mathrm{~J}
\)
From the first law of thermodynamics, we get
\(
\Delta \mathrm{W}=\mathrm{P} \Delta \mathrm{V}
\)
If \(\mathrm{P}\) is the average pressure between points \(A\) and \(B\) and \(\triangle V\) is the change in volume of the system while going from point \(A\) to \(B\), then
\(
\begin{aligned}
& \Delta \mathrm{W}=-\frac{1}{2} \times(200+500) \times 10^3 \times\left(150 \times 10^{-6}\right) \\
& \Delta \mathrm{W}=-\frac{1}{2} \times 700 \times 150 \times 10^{-3} \\
& \Delta \mathrm{W}=-525 \times 10^{-1}=-52.5 \mathrm{~J}
\end{aligned}
\)
Here, negative sign is taken because the final volume is less than the initial volume.
\(
\begin{aligned}
& \Delta U=? \\
& \Delta \mathrm{Q}=\Delta U+\Delta W \\
& \Delta \mathrm{Q}=-294 \mathrm{~J}
\end{aligned}
\)
Here, negative sign indicates that heat is extracted out from the system.
\(
\begin{aligned}
& \Rightarrow-294=\Delta U-52.5 \\
& \Rightarrow \Delta U=-294+52.5=-241.5 \mathrm{~J}
\end{aligned}
\) -
Question 25 of 39
25. Question
The internal energy of a gas is given by \(U=1.5 \mathrm{pV}\). It expands from \(100 \mathrm{~cm}^3\) to \(200 \mathrm{~cm}^3\) against a constant pressure of \(1.0 \times 10^5 \mathrm{~Pa}\). Calculate the heat absorbed by the gas in the process.
CorrectIncorrectHint
Let change in volume of the gas be \(\Delta \mathrm{V}\).
\(
\begin{aligned}
\Delta V & =(200-100) \mathrm{cm}^3=100 \mathrm{~cm}^3 \\
& =10^{-4} \mathrm{~m}^3 \\
p & =1 \times 10^5 \mathrm{~Pa}
\end{aligned}
\)
Change in internal energy of the system, \(\Delta \mathrm{U}=1.5 \mathrm{pV}\)
\(
\begin{aligned}
\Delta \mathrm{U} & =1.5 \times 10^5 \times 10^{-4}=15 \mathrm{~J} \\
\Delta \mathrm{W} & =\mathrm{p} \Delta \mathrm{V} \\
& =10^5 \times 10^{-4}=10 \mathrm{~J}
\end{aligned}
\)
Using the first law of thermodynamics, we get
\(
\Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W}=10+15=25 \mathrm{~J}
\)
Thus, heat absorbed by the system is \(25 \mathrm{~J}\). -
Question 26 of 39
26. Question
A gas is enclosed in a cylindrical vessel fitted with a frictionless piston. The gas is slowly heated for some time. During the process, \(10 \mathrm{~J}\) of heat is supplied and the piston is found to move out \(10 \mathrm{~cm}\). Find the increase in the internal energy of the gas. The area of cross-section of the cylinder \(=4 \mathrm{~cm}^2\) and the atmospheric pressure \(=100 \mathrm{kPa}\)
CorrectIncorrectHint
Given Heat supplied to the system, \(\Delta \mathrm{Q}=10 \mathrm{~J}\)
Change in volume of the system, \(\Delta V=\) Area of cross section \(\times\) Displacement of the piston
\(
\begin{aligned}
& =\mathrm{A} \times 10 \mathrm{~cm} \\
& =(4 \times 10) \mathrm{cm}^3=40 \times 10^{-6} \mathrm{~m}^3 \\
& \mathrm{P}=100 \mathrm{kPa} \\
& \Delta \mathrm{W}=\mathrm{P} \Delta \mathrm{V}=100 \times 10^3 \times 40 \times 10^{-6} \mathrm{~m}^3 \\
& =4 \mathrm{~J} \\
& \Delta \mathrm{U}=?
\end{aligned}
\)
Using the first law of thermodynamics, we get
\(
\begin{aligned}
& 10=\Delta U+\Delta W \\
& \Rightarrow 10=\Delta U+4 \\
& \Rightarrow \Delta U=6 J
\end{aligned}
\)
Here, positive sign indicates that the internal energy of the system has increased. -
Question 27 of 39
27. Question
A gas is initially at a pressure of \(100 \mathrm{kPa}\) and its volume is \(2.0 \mathrm{~m}^3\). Its pressure is kept constant and the volume is changed from \(2.0 \mathrm{~m}^3\) to \(2.5 \mathrm{~m}^3\). Its volume is now kept constant and the pressure is increased from \(100 \mathrm{kPa}\) to \(200 \mathrm{kPa}\). The gas is brought back to its initial state, the pressure varying linearly with its volume. (a) Whether the heat is supplied to or extracted from the gas in the complete cycle? (b) How much heat was supplied or extracted?
CorrectIncorrectHint
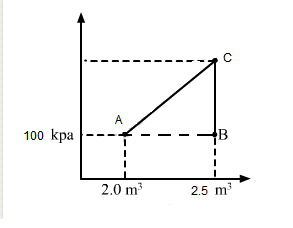
(a) Given
\(
\begin{aligned}
& P_1=100 \mathrm{kPa} \\
& \mathrm{V}_1=2 \mathrm{~m}^3 \\
& \mathrm{~V}_2=2.5 \mathrm{~m}^3 \\
& \Delta \mathrm{V}=0.5 \mathrm{~m}^3
\end{aligned}
\)
Work done, \(\mathrm{W}=\mathrm{P} \Delta \mathrm{V}\)
\(W=100 \times 10^3 \times 0.5\)
\(W=5 \times 10^4 J\)
\(W_{A B}=\) Area under line \(A B=5 \times 10^4 \mathrm{~J}\)
If volume is kept constant for line \(\mathrm{BC}\), then \(\triangle \mathrm{V}=0\).
\(W_{B C}=P \Delta V=0\)
Work done while going from point \(\mathrm{B}\) to \(\mathrm{C}=0\)
When the system comes back to the initial point A from \(C\), work done is equal to area under line \(A C\).
\(W_{C A}=\) Area of triangle \(A B C+\) Area of rectangle under line \(A B\)
Total work done, \(\mathrm{W}=\) Area enclosed by the ABCA
\(W=W_{A C}-W_{A B}\)
From the graph, we see that the area under \(A C\) is greater than the area under \(A B\). We also see that heat is extracted from the system as change in the internal energy is zero.
(b) Amount of heat extracted \(=\) Area enclosed under ABCA
\(
=\frac{1}{2} \times 0.5 \times 100 \times 10^3=25000 J
\) -
Question 28 of 39
28. Question
Consider the cyclic process \(A B C A\), shown in figure below, performed on a sample of \(2.0 \mathrm{~mol}\) of an ideal gas. A total of \(1200 \mathrm{~J}\) of heat is withdrawn from the sample in the process. Find the work done by the gas during the part \(B C\).
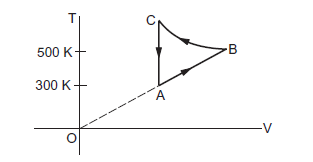CorrectIncorrectHint
Given Number of moles of the gas, \(n=2\)
\(\Delta \mathrm{Q}=-1200 \mathrm{~J}\) (Negative sign shows that heat is extracted out from the system)
\(\Delta U=0\) (During cyclic process)
Using the first law of thermodynamics, we get
\(
\begin{aligned}
& \Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W} \\
& \Rightarrow-1200=0+\left(\mathrm{W}_{\mathrm{AB}}+\mathrm{W}_{\mathrm{BC}}+\mathrm{W}_{\mathrm{CA}}\right)
\end{aligned}
\)
Since the change in volume of the system applies on line CA, work done during CA will be zero.
From the ideal gas equation, we get
\(
\begin{aligned}
& P V=n R T \\
& P \Delta V=n R \Delta T \\
& W=P \Delta V=n R \Delta T \\
& \Rightarrow \Delta Q=\Delta U+\Delta W \\
& \Rightarrow-1200=n R \Delta T+W_{B C}+0 \\
& \Rightarrow-1200=2 \times 8.3 \times 200+W_{B C} \\
& W_{B C}=-400 \times 8.3-1200 \\
& =-4520 \mathrm{~J}
\end{aligned}
\) -
Question 29 of 39
29. Question
The figure below shows the variation in the internal energy \(U\) with the volume \(V\) of \(2.0 \mathrm{~mol}\) of an ideal gas in a cyclic process abcda. The temperatures of the gas at \(b\) and \(c\) are \(500 \mathrm{~K}\) and \(300 \mathrm{~K}\) respectively. Calculate the heat absorbed by the gas during the process.
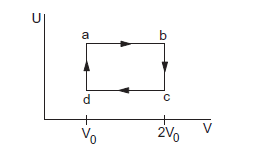CorrectIncorrectHint
Given: Number of moles of the gas, \(n=2\) moles
The system’s volume is constant for lines bc and da.
Therefore,
\(
\Delta V=0
\)
Thus, work done for paths \(d a\) and bc is zero.
\(
\Rightarrow \mathrm{W}_{\mathrm{da}}=\mathrm{W}_{\mathrm{bc}}=0
\)
Since the process is cyclic, \(\Delta U\) is equal to zero.
Using the first law, we get
\(
\begin{aligned}
& \Delta \mathrm{W}=\Delta \mathrm{Q} \\
& \Delta \mathrm{W}=\Delta \mathrm{W}_{\mathrm{AB}}+\Delta \mathrm{W}_{\mathrm{CD}}
\end{aligned}
\)
Since the temperature is kept constant during lines ab and \(c d\), these are isothermal expansions.
Work done during an isothermal process is given by
\(
\begin{aligned}
& \mathrm{W}=\mathrm{nRT} \ln \frac{V_f}{V_i} \\
\end{aligned}
\)
If \(V_f\) and \(V_i\) are the initial and final volumes during the isothermal process, then
\(
\begin{aligned}
& W=n R T_1 \ln \left(\frac{2 V_0}{V_0}\right)+n R T_2 \ln \left(\frac{V_0}{2 V_0}\right) \\
& \mathrm{W}=\mathrm{nR} \times 2.303 \times \log 2 \times(500-300) \\
& \mathrm{W}=2 \times 8.314 \times 2.303 \times 0.301 \times 200 \\
& \mathrm{~W}=2305.31 \mathrm{~J}
\end{aligned}
\) -
Question 30 of 39
30. Question
Find the change in the internal energy of \(2 \mathrm{~kg}\) of water as it is heated from \(0^{\circ} \mathrm{C}\) to \(4^{\circ} \mathrm{C}\). The specific heat capacity of water is \(4200 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\) and its densities at \(0^{\circ} \mathrm{C}\) and \(4^{\circ} \mathrm{C}\) are \(999.9 \mathrm{~kg} \mathrm{~m}^{-3}\) and \(1000 \mathrm{~kg} \mathrm{~m}^{-3}\) respectively. Atmospheric pressure \(=10^5 \mathrm{~Pa}\).
CorrectIncorrectHint
Given Mass of water, \(M=2 \mathrm{~kg}\)
Change in temperature of the system, \(\Delta \theta=4^{\circ} \mathrm{C}=277 \mathrm{~K}\)
Specific heat of water, \(s_w=4200 \mathrm{~J} / \mathrm{kg}-{\circ}{ }^{\circ} \mathrm{C}\)
Initial density, \(\mathrm{p}_0=999.9 \mathrm{~kg} / \mathrm{m}^3\)
Final density, \(p_f=1000 \mathrm{~kg} / \mathrm{m}^3\)
\(
P=10^5 \mathrm{~Pa}
\)
Let change in internal energy be \(\Delta U\).
Using the first law of thermodynamics, we get
\(
\begin{aligned}
& \Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W} \\
& \text { Also, } \Delta \mathrm{Q}=\mathrm{ms} \Delta \theta \\
& \mathrm{W}=\mathrm{P} \Delta \mathrm{V}=\mathrm{P}\left(\mathrm{V}_{\mathrm{f}}-\mathrm{V}_{\mathrm{i}}\right) \\
& \Rightarrow \mathrm{ms} \Delta \theta=\Delta \mathrm{U}+\mathrm{P}\left(\mathrm{V}_0-\mathrm{V}_4\right) \\
& \Rightarrow 2 \times 4200 \times 4=\Delta \mathrm{U}+10^5(\Delta \mathrm{V}) \\
& \Rightarrow 33600=\Delta \mathrm{U}+10^5 \\
& \left(\frac{m}{p_0}-\frac{m}{p_f}\right) \\
& \Rightarrow 33600=\Delta \mathrm{U}+10^5 \times(-0.0000002) \\
& \Rightarrow 33600=\Delta \mathrm{U}-0.02 \\
& \Delta \mathrm{U}=(33600-0.02) \mathrm{J}
\end{aligned}
\) -
Question 31 of 39
31. Question
Calculate the increase in the internal energy of \(10 \mathrm{~g}\) of water when it is heated from \(0^{\circ} \mathrm{C}\) to \(100^{\circ} \mathrm{C}\) and converted into steam at \(100 \mathrm{kPa}\). The density of steam \(=0.6 \mathrm{~kg} \mathrm{~m}^{-3}\). Specific heat capacity of water \(=4200 \mathrm{~J} \mathrm{~kg}^{-1}{ }^{\circ} \mathrm{C}^{-1}\) and the latent heat of vaporization of water \(=2.25 \times 106 \mathrm{~J} \mathrm{~kg}^{-1}\).
CorrectIncorrectHint
Given Mass of water, \(m=10 \mathrm{~g}=0.01 \mathrm{~kg}\)
Pressure, \(P=10^5 \mathrm{~Pa}\)
Specific heat capacity of water, \(\mathrm{c}=1000 \mathrm{~J} / \mathrm{Kg}{ }^{\circ} \mathrm{C}\)
Latent heat, \(\mathrm{L}=2.25 \times 10^6 \mathrm{~J} / \mathrm{Kg}\)
\(\Delta t=\) Change in temperature of the system \(=100^{\circ} \mathrm{C}=373 \mathrm{~K}\)
\(\Delta \mathrm{Q}=\) Heat absorbed to raise the temperature of water from \(0^{\circ} \mathrm{C}\) to \(100^{\circ} \mathrm{C}+\) Latent heat for conversion of water to steam
\(\Delta \mathrm{Q}=m c \Delta t+m L\)
\(=0.01 \times 4200 \times 100+0.01 \times 2.5 \times 10^6\)
\(=4200+25000=29200 \mathrm{~J}\)
\(\Delta \mathrm{W}=\mathrm{P} \Delta \mathrm{V}\)
\(
\begin{aligned}
& \Delta \mathrm{V}=\text { mass }\left(\frac{1}{\text { final density }}-\frac{1}{\text { initial density }}\right) \\
& \Delta V=\left(\frac{0.01}{0.6}\right)-\left(\frac{0.01}{1000}\right)=0.01699 \\
& \Delta \mathrm{W}=\mathrm{P} \Delta \mathrm{V}=0.01699 \times 10^5=1699 \mathrm{~J} \\
& \text { Using the first law, we get } \\
& \Delta \mathrm{Q}=\Delta \mathrm{W}+\Delta \mathrm{U} \\
& \Delta \mathrm{U}=\Delta \mathrm{Q}-\Delta \mathrm{W}=29200-1699 \\
& =27501=2.75 \times 10^4 \mathrm{~J}
\end{aligned}
\) -
Question 32 of 39
32. Question
A geyser heats water flowing at the rate of \(3.0\) litres per minute from \(27^{\circ} \mathrm{C}\) to \(77^{\circ} \mathrm{C}\). If the geyser operates on a gas burner, what is the rate of consumption of the fuel if its heat of combustion is \(4.0 \times 10^4 \mathrm{~J} / \mathrm{g}\)?
CorrectIncorrectHint
Volume of water heated \(=3.0\) litre per minute Mass of water heated, \(\mathrm{m}=3000 \mathrm{~g}\) per minute Increase in temperature,
\(
\triangle T=77^{\circ} \mathrm{C}-27^{\circ} \mathrm{C}=50^{\circ} \mathrm{C}
\)
Specific heat of water, \(c=4.2 \mathrm{Jg}^{-1{ }^{\circ}} \mathrm{C}^{-1}\)
Amount of heat used \(=Q=m c \triangle T\)
or \(Q=3000 \mathrm{gmin}^{-1} \times 4.2 \mathrm{Jg}^{-1{ }^{\circ}} \mathrm{C}^{-1} \times 50^{\circ} \mathrm{C}\)
\(=63 \times 10^4 \mathrm{~J} \mathrm{~min}^{-1}\)
Rate of combustion of fuel \(=\frac{63 \times 10^4 \mathrm{~J} \mathrm{~min}^{-1}}{4.0 \times 10^4 \mathrm{Jg}^{-1}}=15.75 \mathrm{~g} \mathrm{~min}^{-1}\) -
Question 33 of 39
33. Question
What amount of heat must be supplied to \(2.0 \times 10^{-2} \mathrm{~kg}\) of nitrogen (at room temperature) to raise its temperature by \(45^{\circ} \mathrm{C}\) at constant pressure? (Molecular mass of \(\mathrm{N}_2=28 ; R=8.3 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}\).)
CorrectIncorrectHint
Here, mass of gas, \(m=2 \times 10^{-2} \mathrm{~kg}=20 \mathrm{~g}\)
rise in temperature, \(\triangle T=45^{\circ} \mathrm{C}\)
Heat required, triangleQ \(=\)?, Molecular mass, \(M=28\)
Number of moles, \(n=\frac{m}{M}=\frac{20}{28}=0.714\)
As nitrogen is a diatomatic gas, molar specific heat at constant pressure is
\(
C_p=\frac{7}{2} R=\frac{7}{2} \times 8.3 \mathrm{Jmol}^{-1} K^{-1}
\)
As \(\triangle Q=n C_p \triangle T\)
\(
\therefore \triangle Q=0.714 \times \frac{7}{2} \times 8.3 \times 45 J=933.4 J
\) -
Question 34 of 39
34. Question
A cylinder with a movable piston contains 3 moles of hydrogen at standard temperature and pressure. The walls of the cylinder are made of a heat insulator, and the piston is insulated by having a pile of sand on it. By what factor does the pressure of the gas increase if the gas is compressed to half its original volume?
CorrectIncorrectHint
The cylinder is completely insulated from its surroundings. As a result, no heat is exchanged between the system (cylinder) and its surroundings. Thus, the process is adiabatic.
Initial pressure inside the cylinder \(=P_1\)
Final pressure inside the cylinder \(=P_2\)
Initial volume inside the cylinder \(=V_1\)
Final volume inside the cylinder \(=V_2\)
Ratio of specific heats, \(y=1.4\)
For an adiabatic process, we have:
\(
P_1 V_1^\gamma=P_2 V_2^\gamma
\)
The final volume is compressed to half of its initial volume.
\(
\begin{aligned}
& \therefore V_2=\frac{V_1}{2} \\
& P_1\left(V_1\right)^\gamma=P_2\left(\frac{V_1}{2}\right)^\gamma \\
& \frac{P_2}{P_1}=\frac{\left(V_1\right)^\gamma}{\left(\frac{V_1}{2}\right)^\gamma}=(2)^\gamma=(2)^{\frac{1}{4}}=2.64
\end{aligned}
\)
Hence, the pressure increases by a factor of \(2.64\). -
Question 35 of 39
35. Question
In changing the state of a gas adiabatically from an equilibrium state \(A\) to another equilibrium state \(B\), an amount of work equal to \(22.3 \mathrm{~J}\) is done on the system. If the gas is taken from state \(A\) to \(B\) via a process in which the net heat absorbed by the system is \(9.35 \mathrm{cal}\), how much is the net work done by the system in the latter case?
(Take \(1 \mathrm{cal}=4.19 \mathrm{~J})\)CorrectIncorrectHint
The work done \((W)\) on the system while the gas changes from state \(A\) to state \(B\) is \(22.3 \mathrm{~J}\).
This is an adiabatic process. Hence, change in heat is zero.
\(
\therefore \Delta Q=0
\)
\(\Delta W=-22.3 \mathrm{~J}\) (Since the work is done on the system)
From the first law of thermodynamics, we have:
\(
\Delta Q=\Delta U+\Delta W
\)
Where,
\(\Delta U=\) Change in the internal energy of the gas
\(
\begin{aligned}
& \therefore \Delta U=\Delta Q-\Delta W=-(-22.3 \mathrm{~J}) \\
& \Delta U=+22.3 \mathrm{~J}
\end{aligned}
\)
When the gas goes from state \(A\) to state \(B\) via a process, the net heat absorbed by the system is:
\(
\Delta Q=9.35 \mathrm{cal}=9.35 \times 4.19=39.1765 \mathrm{~J}
\)
Heat absorbed, \(\Delta Q=\Delta U+\Delta Q\)
\(
\begin{aligned}
& \therefore \Delta W=\Delta Q-\Delta U \\
& =39.1765-22.3 \\
& =16.9 \mathrm{~J}
\end{aligned}
\)
Therefore, \(16.9 \mathrm{~J}\) of work is done by the system. -
Question 36 of 39
36. Question
A steam engine delivers \(5.4 \times 10^8 \mathrm{~J}\) of work per minute and services \(3.6 \times 10^9 \mathrm{~J}\) of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?
CorrectIncorrectHint
Work done per minute, output \(=5.4 \times 10^8 \mathrm{~J}\)
Heat absorbed per minute, input \(=3.6 \times 10^9 \mathrm{~J}\)
Efficiency = \(\eta\) = output/input, \(=\left(5.4 \times 10^{\wedge} 8\right) /\left(3.6 \times x 10^{\wedge} 9\right)=0.15\)
\(\% \eta=0.15 \times 100=15\)
Heat energy wasted /minute
= Heat energy absorbed / minute – Useful work done / minute
\(=3.6 \times 10^9-5.4 \times 10^8\)
\(=(3.6-0.54) \times 10^9=3.1 \times 10^9 \mathrm{~J}\) -
Question 37 of 39
37. Question
An electric heater supplies heat to a system at a rate of \(100 \mathrm{~W}\). If the system performs work at a rate of 75 joules per second. At what rate is the internal energy increasing?
CorrectIncorrectHint
Here \(\triangle Q=100 W=100 \mathrm{~J} / \mathrm{s}\)
\(
\Delta W=75 \mathrm{~J} / \mathrm{s}
\)
Since \(\triangle Q=\triangle U+\triangle W\)
\(
=100-75=25 W
\) -
Question 38 of 39
38. Question
A thermodynamic system is taken from an original state to an intermediate state by the linear process is shown in the figure below.
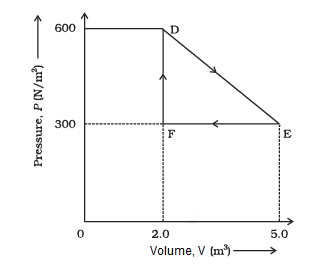
Its volume is then reduced to the original value from E to F by an isobaric process. Calculate the total work done by the gas from D to E to F.
CorrectIncorrectHint
Total work done by the gas from \(D\) to \(E\) to \(F=\) Area of \(\triangle D E F\)
Area of \(\triangle \mathrm{DEF}=\frac{1}{2} D E \times E F\)
Where,
\(\mathrm{DF}=\) Change in pressure
\(=600 \mathrm{~N} / \mathrm{m}^2-300 \mathrm{~N} / \mathrm{m}^2\)
\(=300 \mathrm{~N} / \mathrm{m}^2\)
\(\mathrm{FE}=\) Change in volume
\(=5.0 \mathrm{~m}^3-2.0 \mathrm{~m}^3\)
\(=3.0 \mathrm{~m}^3\)
Area of \(\triangle \mathrm{DEF}=\frac{1}{2} \times 300 \times 3=450 \mathrm{~J}\)
Therefore, the total work done by the gas from \(D\) to \(E\) to \(F\) is \(450 \mathrm{~J}\). -
Question 39 of 39
39. Question
A refrigerator is to maintain eatables kept inside at \(9^{\circ} \mathrm{C}\). If room temperature is \(36^{\circ} \mathrm{C}\), calculate the coefficient of performance.
CorrectIncorrectHint
Temperature inside the refrigerator, \(T_1=9^{\circ} \mathrm{C}=282 \mathrm{~K}\)
Room temperature, \(T_2=36^{\circ} \mathrm{C}=309 \mathrm{~K}\)
\(
\begin{aligned}
& \text { Coefficient of performance }=\frac{T_1}{T_2-T_2} \\
& =\frac{282}{309-282} \\
& =10.4
\end{aligned}
\)
Therefore, the coefficient of performance of the given refrigerator is \(10.4\).