HCV MCQs
Quiz Summary
0 of 102 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 102 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 102
1. Question
Is heat a conserved quantity?
CorrectIncorrectHint
Yes, heat is a conserved quantity. Suppose two bodies A and B are at different temperatures, wherein A is higher and B is lower. When they are brought in contact, the heat given by A is equal to the heat gained by B. Thus, the heat is conserved in the system.
Here, we have ignored the heat exchanged with the surroundings. If we consider the surroundings, the heat of the system will be conserved.
-
Question 2 of 102
2. Question
In a calorimeter, the heat given by the hot object is assumed to be equal to the heat taken by the cold object. Does it mean that the heat of the two objects taken together remains constant?
CorrectIncorrectHint
Yes, heat of the two objects taken together remains constant. If no heat is lost to the surroundings, the heat of the two bodies taken together actually remains conserved.
-
Question 3 of 102
3. Question
What is the specific heat capacity of melting ice?
CorrectIncorrectHint
\(
\text { The specific heat capacity of melting ice is } 0.50 \mathrm{cal} / \mathrm{g}^{-} \mathrm{C} \text { or } 2093 \mathrm{~J} / \mathrm{kg}-\mathrm{K} \text {. }
\) -
Question 4 of 102
4. Question
What is the specific heat capacity of boiling water?
CorrectIncorrectHint
\(
\text { The specific heat capacity of boiling water is } 0.46 \mathrm{cal} / \mathrm{g}-{ }^{\circ} \mathrm{C} \text { or } 1926 \mathrm{~J} / \mathrm{kg}-\mathrm{K} \text {. }
\) -
Question 5 of 102
5. Question
The specific heat capacity of a body depends on
CorrectIncorrectHint
The heat capacity of a body is due to its material properties. Due to different molecular structures, different bodies have a different capacity to absorb heat. Therefore, the specific heat of a body depends on the material of the body.
-
Question 6 of 102
6. Question
Water equivalent of a body is measured in
CorrectIncorrectHint
Since water equivalent of a body is the mass of the water having the same heat capacity as the given body, the water equivalent is measured in kilogram.
-
Question 7 of 102
7. Question
When a hot liquid is mixed with a cold liquid, the temperature of the mixture
CorrectIncorrectHint
is undefined for some time and then becomes nearly constant.
When hot liquid is mixed with cold liquid, the molecules collide and transfer heat. When heat is transferred, the temperature is undefined. Once the heat energy is shared by the molecules, the system reaches equilibrium and the temperature becomes nearly constant.
-
Question 8 of 102
8. Question
Which of the following pairs represent units of the same physical quantity?
CorrectIncorrectHint
Joule and calorie
One calorie is defined as the amount of heat needed to raise the temperature of \(1 \mathrm{~g}\) of water from \(14.5^{\circ}\) to \(15.5^{\circ}\) at the pressure of \(1 \mathrm{~atm}\). Heat is a form of energy and the unit of energy is joule.
Therefore, joule and calorie represent energy. -
Question 9 of 102
9. Question
Which of the following pairs of physical quantities maybe represented in the same unit?
CorrectIncorrectHint
Heat and Work
As work done in raising temperature of a body is actually the heat supplied to the body, heat and work may be represented in the same unit.
-
Question 10 of 102
10. Question
Two bodies at different temperatures are mixed in a calorimeter. Which of the following quantities remains conserved?
CorrectIncorrectHint
Total internal energy of the two bodies
When two bodies at different temperatures are mixed in the calorimeter, heat flows from one body to the other due to the temperature difference. This results in change in the internal energy of the individual bodies. There is no exchange of heat with the surrounding in the calorimeter. Thus, the total internal energy of the bodies remain conserved as no external work is done on them.
-
Question 11 of 102
11. Question
The mechanical equivalent of heat
CorrectIncorrectHint
is dimensionless
If the mechanical work done \((\mathrm{W})\) produces the same temperature change as heat \((\mathrm{H})\),then the mechanical equivalent of heat \((J)\) is equal to \(W / H\). Thus,
\(
\mathrm{J}=\mathrm{W} / \mathrm{H}
\)
Since the unit of work and heat is the same, mechanical equivalent of heat is dimensionless. -
Question 12 of 102
12. Question
The heat capacity of a body depends on
CorrectIncorrectHint
(c) the mass of the body
(d) the material of the body
The bigger the body, the larger is its capacity to absorb heat. Therefore, the heat capacity of a body depends on the mass of the body. Also, different bodies have different heat capacities due to their material properties, i.e. due to their molecular structure, the heat capacity of a body depends on the material of the body. -
Question 13 of 102
13. Question
The ratio of specific heat capacity to molar heat capacity of a body
CorrectIncorrectHint
depends of the molecular weight of the body
Specific heat capacity of a body,
\(
s=\frac{Q}{m \Delta \theta}
\)
Here,
\(Q=\) Heat supplied
\(\mathrm{m}=\) Mass of body
\(\Delta \theta=\) Change in temperature
Molar heat capacity of a body,
\(
C=\frac{Q}{n \Delta \theta}
\)
Here,
\(Q=\) Heat supplied
\(n=\) Number of moles
\(\Delta \theta=\) Change in temperature
\(\therefore\) The ratio of the specific heat capacity and molar heat capacity is given by
\(
\frac{s}{C}=\frac{\frac{Q}{m \Delta \theta}}{\frac{Q}{n \Delta \theta}}=\frac{n}{m}=\frac{n}{n M}=\frac{1}{M}
\)
Here,
\(M=\) Molar mass related to number of moles
\(
\mathrm{m}=\text { Mass }
\)
As the value of \(\mathrm{M}\) is different for different bodies of different composition, the ratio cannot be a universal constant.
Also, the ratio is independent of the mass of the body.
The ratio of the specific heat and molar heat capacity depends on the molecular weight of the body.
Clearly, the unit of molecular weight is \(\mathrm{kg} / \mathrm{mole}\). So, the ratio that depends only on the molecular weight cannot be dimensionless. -
Question 14 of 102
14. Question
If heat is supplied to a solid, its temperature
CorrectIncorrectHint
(b) may increase
(c) may remain constant
When heat is supplied to a solid, it is used up either to increase the temperature of the body or to change its state from one form to another by breaking the bonds between the molecules (without raising the temperature).
When heat is supplied to the solid, the internal energy of the solid increases, so the temperature does not decrease. -
Question 15 of 102
15. Question
The temperature of a solid object is observed to be constant during a period. In this period
CorrectIncorrectHint
(a) heat may have been supplied to the body
(b) heat may have been extracted from the body
If there is no temperature change in a solid object, there is a possibility that the heat might have been supplied to the body that was used up in breaking the bond of the molecules, changing the state of the solid. This is why the temperature of the solid remians constant. Similar is the case when the heat is extracted from the body to change its state.
Since there is a possibility of supplying or extracting heat from the solid, we cannot say that heat is not supplied to the solid or is not extracted from the solid. -
Question 16 of 102
16. Question
The temperature of an object is observed to rise in a period. In this period
CorrectIncorrectHint
(c) heat may have been supplied to it
(d) work may have been done on it
If the temperature of an object rises in a period, then there are two possibilities. The heat may have been supplied to it, leading to an increase of the internal energy of the object. That will increase the temperature of the body.
The second possibility is that some work may have been done on it, again leading to an increase of the internal energy of the body. That will also increase the temperature of the body. -
Question 17 of 102
17. Question
Heat and work are equivalent. This means,
CorrectIncorrectHint
the temperature of a body can be increased by doing work on it
According to the statement “heat and work are equivalent”, heat supplied to the body increases its temperature. Similarly, work done on the body also increases its temperature.
For example: If work is done on rubbing the hands against each other, the temperature of the hands increases. So, we can say that heat and work are equivalent.
When heat is supplied to a body, we do not do work on it. When we are doing work on a body, it does not mean we are supplying heat to the body. Also, a body at rest cannot be set in motion along a line by supplying heat to it. So, these statements do not justify the equivalence of heat and work. -
Question 18 of 102
18. Question
An aluminium vessel of mass \(0.5 \mathrm{~kg}\) contains \(0.2 \mathrm{~kg}\) of water at \(20^{\circ} \mathrm{C}\). A block of iron of mass \(0.2 \mathrm{~kg}\) at \(100^{\circ} \mathrm{C}\) is gently put into the water. Find the equilibrium temperature of the mixture. Specific heat capacities of aluminium, iron and water are \(910 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\), \(470 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\) and \(4200 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\) respectively.
CorrectIncorrectHint
Given
Mass of aluminium \(=0.5 \mathrm{~kg}\)
Mass of water \(=0.2 \mathrm{~kg}\)
Mass of iron \(=0.2 \mathrm{~kg}\)
Specific heat of aluminium \(=910 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\)
Specific heat of iron \(=470 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\)
Specific heat of water \(=4200 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\)
Let the equilibrium temperature of the mixture be \(T\).
Temperature of aluminium and water \(=20^{\circ} \mathrm{C}=273+20=293 \mathrm{~K}\)
Temperature of iron \(=100^{\circ} \mathrm{C}=273+100=373 \mathrm{~K}\)
Heat lost by iron, \(\mathrm{H}_1=0.2 \times 470 \times(373-\mathrm{T})\)
Heat gained by water \(=0.2 \times 4200 \times(T-293)\)
Heat gained by iron \(=0.5 \times 910 \times(\mathrm{T}-293)\)
Total heat gained by water and iron, \(\mathrm{H}_2=0.5 \times 910(\mathrm{~T}-293)+0.2 \times 4200 \times(\mathrm{T}-293)\)
\(
\mathrm{H}_2=(\mathrm{T}-293)[0.5 \times 910+0.2 \times 4200]
\)
We know,
Heat gain \(=\) Heat lost
\(
\begin{aligned}
& \Rightarrow(T-293)[0.5 \times 910+0.2 \times 4200]=0.2 \times 470 \times(373-\mathrm{T}) \\
& \Rightarrow(\mathrm{T}-293)(455+840)=94(373-\mathrm{T}) \\
& \Rightarrow(T-293) \frac{1295}{94}=(373-T) \\
& (T-293) \times 14=(373-T) \\
& \Rightarrow 14 \mathrm{~T}-293 \times 14=373-\mathrm{T} \\
& \Rightarrow 15 \mathrm{~T}=373+4102=4475 \\
& \Rightarrow T=\frac{4475}{15}=298.33 \mathrm{~K} \approx 298 \mathrm{~K} \\
& \therefore \mathrm{T}=(298-273)^{\circ} \mathrm{C}=25^{\circ} \mathrm{C} \\
& \therefore \text { Final temperature }=25^{\circ} \mathrm{C}
\end{aligned}
\) -
Question 19 of 102
19. Question
A piece of iron of mass \(100 \mathrm{~g}\) is kept inside a furnace for a long time and then put in a calorimeter of water equivalent \(10 \mathrm{~g}\) containing \(240 \mathrm{~g}\) of water at \(20^{\circ} \mathrm{C}\). The mixture attains an equilibrium temperature of \(60^{\circ} \mathrm{C}\). Find the temperature of the furnace. Specific heat capacity of iron \(=470 \mathrm{~J} \mathrm{~kg}^{-1}{ }^{\circ} \mathrm{C}^{-1}\).
CorrectIncorrectHint
Mass of iron \(=100 \mathrm{~g}\)
Water equivalent of calorimeter \(=10 \mathrm{~g}\)
Mass of water \(=240 \mathrm{gm}\)
Let the temperature of surface be \(\theta^{\circ} \mathrm{C}\).
Specific heat capacity of iron \(=470 \mathrm{~J} \mathrm{~kg}^{-1}{ }^{\circ} \mathrm{C}^{-1}\)
Total heat gained \(=\) Total heat lost
\(
\begin{aligned}
& \Rightarrow \frac{100}{1000} \times 470 \times\left(\theta-60^{\circ}\right)=\frac{240+10}{1000} \times 4200 \times(60-20) \\
& \Rightarrow 47 \theta-47 \times 60=25 \times 42 \times 40 \\
& \Rightarrow \theta=\frac{42000+2820}{47}=\frac{44820}{47} \\
& =953.61^{\circ} \mathrm{C}
\end{aligned}
\) -
Question 20 of 102
20. Question
The temperatures of equal masses of three different liquids \(A, B\) and \(C\) are \(12^{\circ} \mathrm{C}, 19^{\circ} \mathrm{C}\) and \(28^{\circ} \mathrm{C}\) respectively. The temperature when \(A\) and \(B\) are mixed is \(16^{\circ} \mathrm{C}\), and when \(B\) and \(C\) are mixed, it is \(23^{\circ} \mathrm{C}\). What will be the temperature when \(A\) and \(C\) are mixed?
CorrectIncorrectHint
Let \(m\) be the mass of each liquid.
When \(A\) and \(B\) are mixed,
Heat lost by \(B=\) Heat gained by \(A\)
\(\mathrm{ms}_{\mathrm{B}} \Delta \mathrm{T}_{\mathrm{B}}=-\mathrm{ms}_{\mathrm{A}} \Delta \mathrm{T}_{\mathrm{A}}\)
\(s_B(19-16)=-s_A(12-16)\) \(3 s_B=4 s_A \ldots\) (1)When B and C are mixed,
Heat lost by \(C=\) Heat gained by \(B\)
\(\mathrm{ms}_{\mathrm{C}} \Delta \mathrm{T}_{\mathrm{C}}=-\mathrm{ms}_{\mathrm{B}} \Delta \mathrm{T}_{\mathrm{B}}\)
\(\mathrm{s}_{\mathrm{C}}(28-23)=-\mathrm{ms}_{\mathrm{B}}(19-23)\)
\(5 s_C=4 s_B \ldots(2)\)From (1) and (2), we get:
\(
16 \mathrm{~s}_{\mathrm{A}}=12 \mathrm{~s}_{\mathrm{B}}=15 \mathrm{~s}_{\mathrm{C}} \ldots \text { (3) }
\)
When \(\mathrm{A}\) and \(\mathrm{C}\) are mixed,
Let \(\theta\) be the final temperature attained
Heat lost by \(C=\) Heat gained by \(A\)
\(m s_C \Delta T_C=-m_A \Delta T_A\)
\(
\mathrm{s}_{\mathrm{C}}(28-\theta)=-\mathrm{s}_{\mathrm{A}}(12-\theta)
\)
Using (3), we get
\(
\begin{aligned}
& 16 \mathrm{~s}_{\mathrm{A}}(28-\theta)=15 \mathrm{~s}_{\mathrm{A}}(\theta-12) \\
& \theta=20.26^{\circ} \mathrm{C}=20.3^{\circ} \mathrm{C}
\end{aligned}
\) -
Question 21 of 102
21. Question
Four \(2 \mathrm{~cm} \times 2 \mathrm{~cm} \times 2 \mathrm{~cm}\) cubes of ice are taken out from a refrigerator and are put in \(200 \mathrm{ml}\) of a drink at \(10^{\circ} \mathrm{C}\). (a) Find the temperature of the drink when thermal equilibrium is attained in it. (b) If the ice cubes do not melt completely, find the amount melted. Assume that no heat is lost to the outside of the drink and that the container has negligible heat capacity. Density of ice \(=900 \mathrm{~kg} \mathrm{~m}^{-3}\), density of the drink \(=1000 \mathrm{~kg} \mathrm{~m}^{-3}\), specific heat capacity of the drink \(=4200 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\), latent heat of fusion of ice \(=3.4 \times 10^5 \mathrm{~J} \mathrm{~kg}^{-1}\).
CorrectIncorrectHint
(a)
Given:-
Number of ice cubes \(=4\)
Volume of each ice cube \(=(2 \times 2 \times 2)=8 \mathrm{~cm}^3\)
Density of ice \(=900 \mathrm{~kg} \mathrm{~m}^{-3}\)
Total mass of ice, \(\mathrm{m}_{\mathrm{i}}=\left(4 \times 8 \times 10^{-6} \times 900\right)=288 \times 10^{-4} \mathrm{~kg}\)
Latent heat of fusion of ice, \(L_i=3.4 \times 10^5 \mathrm{~J} \mathrm{~kg}^{-1}\)
Density of the drink \(=1000 \mathrm{~kg} \mathrm{~m}^{-3}\)
Volume of the drink \(=200 \mathrm{ml}\)
Mass of the drink \(=\left(200 \times 10^{-6}\right) \times 1000 \mathrm{~kg}\)
Let us first check the heat released when temperature of \(200 \mathrm{ml}\) changes from \(10^{\circ} \mathrm{C}\) to \(0^{\circ} \mathrm{C}\). \(\mathrm{H}_{\mathrm{w}}=\left(200 \times 10^{-6}\right) \times 1000 \times 4200 \times(10-0)=8400 \mathrm{~J}\)
Heat required to change four \(8 \mathrm{~cm}^3\) ice cubes into water \(\left(\mathrm{H}_{\mathrm{i}}\right)=\mathrm{m}_{\mathrm{i}} \mathrm{L}_{\mathrm{i}}=\left(288 \times 10^{-4}\right) \times\left(3.4 \times 10^5\right)=9792 \mathrm{~J}\)
Since the heat required for melting the four cubes of the ice is greater than the heat released by water ( \(H_i>H_w\) ), some ice will remain solid and there will be equilibrium between ice and water. Thus, the thermal equilibrium will be attained at \(0^{\circ} \mathrm{C}\).
(b)
Equilibrium temperature of the cube and the drink \(=0^{\circ} \mathrm{C}\)
Let \(M\) be the mass of melted ice.
Heat released when temperature of \(200 \mathrm{ml}\) changes from \(10^{\circ} \mathrm{C}\) to \(0^{\circ} \mathrm{C}\) is given by
\(
H_w=\left(200 \times 10^{-6}\right) \times 1000 \times 4200 \times(10-0)=8400 \mathrm{~J}
\)
Thus,
\(
M \times\left(3.4 \times 10^5\right)=8400 \mathrm{~J}
\)
Therefore,
\(
M=0.0247 \mathrm{Kg}=25 \mathrm{~g}
\) -
Question 22 of 102
22. Question
Indian style of cooling drinking water is to keep it in a pitcher having porous walls. Water comes to the outer surface very slowly and evaporates. Most of the energy needed for evaporation is taken from the water itself and the water is cooled down. Assume that a pitcher contains \(10 \mathrm{~kg}\) of water and \(0.2 \mathrm{~g}\) of water comes out per second. Assuming no backward heat transfer from the atmosphere to the water, calculate the time in which the temperature decreases by \(5^{\circ} \mathrm{C}\). Specific heat capacity of water \(=4200 \mathrm{~J} \mathrm{~kg}^{-1}{ }^{\circ} \mathrm{C}^{-1}\) and latent heat of vaporization of water \(=2.27 \times 10^6 \mathrm{~J} \mathrm{~kg}^{-1}\).
CorrectIncorrectHint
Given
Specific heat of water \(S=4200 \mathrm{~J} \mathrm{~kg}^{-1}{ }^{\circ} \mathrm{C}^{-1}\)
Latent heat of vapourisation of water \(L=2.27 \times 10^6 \mathrm{~J} \mathrm{~kg}^{-1}\)
Mass, \(M=0.2 \mathrm{~g}=0.0002 \mathrm{~kg}\)
Let us first calculate the amount of energy required to decrease the temperature of \(10 \mathrm{~kg}\) of water by \(5^{\circ} \mathrm{C}\).
\(
\begin{aligned}
& U_1=10 \times 4200 \mathrm{~J} / \mathrm{kg}^{\circ} \mathrm{C} \times 5^{\circ} \mathrm{C} \\
& U_1=210,000=21 \times 10^4 \mathrm{~J}
\end{aligned}
\)
Let the time in which the temperature is decreased by \(5^{\circ} \mathrm{C}\) be \(\mathrm{t}\).
Energy required per second for evaporation of water (at the rate of \(0.2 \mathrm{~g} / \mathrm{sec}\) ) is given by
\(
\begin{aligned}
& U_2=M L \\
& U_2=\left(2 \times 10^{-4}\right) \times\left(2.27 \times 10^6\right)=454 \mathrm{~J}
\end{aligned}
\)
Total energy required to decrease the temperature of the water \(=454 \times \mathrm{t}\)
\(
=21 \times 10^4 \mathrm{~J}
\)
Now,
\(
t=\frac{21 \times 10^4}{454} \text { seconds }
\)
The time taken in minutes is given by
\(
t=\frac{21 \times 10^4}{454 \times 60}=7.7 \text { minutes }
\)
\(\therefore\) The time required to decrease the temperature by \(5^{\circ} \mathrm{C}\) is \(7.7\) minutes. -
Question 23 of 102
23. Question
A cube of iron (density \(=8000 \mathrm{~kg} \mathrm{~m}^{-3}\), specific heat capacity \(=470 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\) ) is heated to a high temperature and is placed on a large block of ice at \(0^{\circ} \mathrm{C}\). The cube melts the ice below it, displaces the water and sinks. In the final equilibrium position, its upper surface just goes inside the ice. Calculate the initial temperature of the cube. Neglect any loss of heat outside the ice and the cube. The density of ice \(=900 \mathrm{~kg} \mathrm{~m}^{-3}\) and the latent heat of fusion of ice \(=3.36 \times 10^5 \mathrm{~J} \mathrm{~kg}^{-1}\).
CorrectIncorrectHint
Given
Density of the iron cube \(=8000 \mathrm{~kg} \mathrm{~m}^{-3}\)
Density of the ice cube \(=900 \mathrm{~kg} \mathrm{~m}^{-3}\)
Specific heat capacity, S \(=470 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\)
Latent heat of fusion of ice, \(L=3.36 \times 10^5 \mathrm{~J} \mathrm{~kg}^{-1}\)
Let the volume of the cube be V.
Volume of water displaced \(=\mathrm{V}\)
Mass of cube, \(m=8000 \mathrm{~V} \mathrm{~kg}\)
Mass of the ice melted, \(M=900 \mathrm{~V}\)
Let the initial temperature of the iron cube be T K.
Then,
Heat gained by the ice \(=\) Heat lost by the iron cube
\(
\begin{aligned}
& \mathrm{m} \times \mathrm{S} \times(\mathrm{T}-273)=\mathrm{M} \times \mathrm{L} \\
& \Rightarrow 8000 \mathrm{~V} \times 470 \times(\mathrm{T}-273)=900 \mathrm{~V} \times\left(3.36 \times 10^5\right) \\
& \Rightarrow 376 \times 10^4 \times(\mathrm{T}-273)=3024 \times 10^5 \\
& \Rightarrow T=\frac{30240+102648}{376} \\
& \Rightarrow T=\frac{132888}{376} K \\
& \Rightarrow T=353.425 K \approx 353 K \\
& \Rightarrow T=353 K-273 K \\
& \Rightarrow T=80^{\circ} \mathrm{C}
\end{aligned}
\) -
Question 24 of 102
24. Question
\(1 \mathrm{~kg}\) of ice at \(0^{\circ} \mathrm{C}\) is mixed with \(1 \mathrm{~kg}\) of steam at \(100^{\circ} \mathrm{C}\). What will be the composition of the system when thermal equilibrium is reached ? Latent heat of fusion of ice \(=3.36 \times 10^5 \mathrm{~J} \mathrm{~kg}^{-1}\) and latent heat of vaporization of water \(=2.26 \times 10^6 \mathrm{~J} \mathrm{~kg}^{-1}\).
CorrectIncorrectHint
Given
Amount of ice at \(0^{\circ} \mathrm{C}=1 \mathrm{~kg}\)
Amount of steam at \(100^{\circ} \mathrm{C}=1 \mathrm{~kg}\)
Latent heat of fusion of ice \(=3.36 \times 10^3 \mathrm{~J} \mathrm{~kg}^{-1}\)
Latent heat of vapourisation of water \(=2.26 \times 10^6 \mathrm{~J} \mathrm{~kg}^{-1}\)
We can observe that the latent heat of fusion of ice \(\left(3.36 \times 10^5 \mathrm{~J} \mathrm{~kg}^{-1}\right)\) is smaller that latent heat of vapouisation of water \(\left(2.26 \times 10^6\right)\). Therefore, ice will first change into water as less heat is required for this and there will be equilibrium between steam and water.
Heat absorbed by the ice when it changes into water \(\left(Q_1\right)=1 \times\left(3.36 \times 10^5\right) \mathrm{J}\)
Heat absorbed by the water formed to change its temperature from \(0^{\circ} \mathrm{C}\) to \(100^{\circ} \mathrm{C}\left(Q_2\right)=1 \times 4200 \times 100=\) \(4.2 \times 10^5 \mathrm{~J}\)
Total heat absorbed by the ice to raise the temperature to \(100^{\circ} \mathrm{C}, \mathrm{Q}=\mathrm{Q}_1+\mathrm{Q}_2=3.36 \times 10^5+4.2 \times 10^5=\) \((3.36+4.2) \times 10^5=7.56 \times 10^5 \mathrm{~J}\)
The heat required to change ice into water at \(100^{\circ} \mathrm{C}\) is supplied by the steam. This heat will be released by the steam and will then change into water.If all the steam gets converted into water, heat released by steam, \(Q^{\prime}=1 \times\left(2.26 \times 10^6\right) \mathrm{J}=2.26 \times 10^6 \mathrm{~J}\)
Amount of heat released is more than that required by the ice to get converted into water at \(100^{\circ} \mathrm{C}\). Thus,
Extra heat \(=Q-Q^{\prime}\)
\(=(2.26-0.756) \times 10^6\)
\(=1.506 \times 10^6\)
Let the mass of steam that is condensed into water be \(\mathrm{m}\). Thus,
\(
m=\frac{7.56 \times 10^5}{2.26 \times 10^6}=0.335 \mathrm{~kg}=335 \mathrm{gm}
\)
Total amount of water at \(100^{\circ} \mathrm{C}=1000+335=1335 \mathrm{~g}=1.335 \mathrm{~g}\)
Steam left \(=1-0.335=0.665 \mathrm{~kg}=665 \mathrm{gm}\) -
Question 25 of 102
25. Question
Calculate the time required to heat \(20 \mathrm{~kg}\) of water from \(10^{\circ} \mathrm{C}\) to \(35^{\circ} \mathrm{C}\) using an immersion heater rated \(1000 \mathrm{~W}\). Assume that \(80 \%\) of the power input is used to heat the water. Specific heat capacity of water \(=4200 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\).
CorrectIncorrectHint
Given
Power rating of the immersion rod, \(\mathrm{P}=1000 \mathrm{~W}\)
Specific heat of water, \(\mathrm{S}=4200 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\)
Mass of water, \(M=20 \mathrm{~kg}\)
Change in temperature, \(\Delta \mathrm{T}=25^{\circ} \mathrm{C}\)
Total heat required to raise the temperature of \(20 \mathrm{~kg}\) of water from \(10^{\circ} \mathrm{C}\) to \(35^{\circ} \mathrm{C}\) is given by
\(
\begin{aligned}
& Q=M \times S \times \Delta T \\
& Q=20 \times 4200 \times 25 \\
& Q=20 \times 4200 \times 25=21 \times 10^5 \mathrm{~J}
\end{aligned}
\)
Let the time taken to heat \(20 \mathrm{~kg}\) of water from \(10^{\circ} \mathrm{C}\) to \(35^{\circ} \mathrm{C}\) be t. Only \(80 \%\) of the immersion rod’s heat is useful for heating water. Thus,
Energy of the immersion rod utilised for heating the water \(=\mathrm{t} \times(0.80) \times 1000 \mathrm{~J}\)
\(
\begin{aligned}
& \mathrm{t} \times(0.80) \times 1000 \mathrm{~J}=21 \times 10^5 \mathrm{~J} \\
& t=\frac{21 \times 10^5}{800}=2625 \mathrm{~s} \\
& \Rightarrow t=\frac{2625}{60}=43.75 \mathrm{~min} \approx 44 \mathrm{~min}
\end{aligned}
\) -
Question 26 of 102
26. Question
On a winter day the temperature of the tap water is \(20^{\circ} \mathrm{C}\) whereas the room temperature is \(5^{\circ} \mathrm{C}\). Water is stored in a tank of capacity \(0.5 \mathrm{~m}^3\) for household use. If it were possible to use the heat liberated by the water to lift a \(10 \mathrm{~kg}\) mass vertically, how high can it be lifted as the water comes to the room temperature? Take \(g=10 \mathrm{~ms}^{-2}\)
CorrectIncorrectHint
Given
Initial temperature of the water, \(\mathrm{T}_{\mathrm{i}}=20^{\circ} \mathrm{C}\)
Final temperature of the water (room temperature), \(T_f=5^{\circ} \mathrm{C}\)
Change in temeprature, \(\Delta \mathrm{T}=20^{\circ} \mathrm{C}-5^{\circ} \mathrm{C}=15^{\circ} \mathrm{C}\)
Volume of water \(=0.5 \mathrm{~m}^3\)
Density of water, \(d=1000 \mathrm{~kg} / \mathrm{m}^3\)
Mass of the water, \(M=(0.5 \times 1000) \mathrm{kg}=500 \mathrm{~kg}\)
Heat liberated as the temperature of water changes from \(20^{\circ} \mathrm{C}\) to \(5^{\circ} \mathrm{C}\) is given by \(\mathrm{Q}=\mathrm{M} \times \mathrm{S} \times \Delta \mathrm{T}\)
\(Q=(500 \times 4200 \times 15) J\)
\(\mathrm{Q}=(500 \times 4200 \times 15) J\)
\(Q=(75 \times 420 \times 1000) J\)
\(Q=31500 \times 1000 \mathrm{~J}=315 \times 10^5 \mathrm{~J}\)
Let the height to which the mass is lifted be \(h\).
The energy required to lift the block \(=\mathrm{mgh}=10 \times 10 \times \mathrm{h}=100 \mathrm{~h}\)
Acording to the question,
\(
\begin{aligned}
& Q=\text { mgh } \\
& \Rightarrow 100 \mathrm{~h}=315 \times 10^5 \mathrm{~J} \\
& \Rightarrow \mathrm{h}=315 \times 10^3 \mathrm{~m}=315 \mathrm{~km}
\end{aligned}
\) -
Question 27 of 102
27. Question
A bullet of mass \(20 \mathrm{~g}\) enters into a fixed wooden block with a speed of \(40 \mathrm{~m} \mathrm{~s}^{-1}\) and stops in it. Find the change in internal energy during the process.
CorrectIncorrectHint
Given
Mass of bullet, \(\mathrm{m}=20 \mathrm{~g}=0.02 \mathrm{~kg}\)
Initial velocity of the bullet, \(u=40 \mathrm{~m} / \mathrm{s}\)
Final velocity of the bullet \(=0 \mathrm{~m} / \mathrm{s}\)
Initial kinetic energy of the bullet \(=\frac{1}{2} m u^2=\frac{1}{2} \times 0.02 \times 40 \times 40=16 J\)
Final kinetic energy of the bullet \(=0\)
Change in energy of the bullet \(=16 \mathrm{~J}\)
It is given that the bullet enters the block and stops inside it. The total change in its kinetic energy is responsible for the change in the internal energy of the block.
\(\therefore\) Change in internal energy of the block \(=\) Change in energy of the bullet \(=16 \mathrm{~J}\) -
Question 28 of 102
28. Question
A \(50 \mathrm{~kg}\) man is running at a speed of \(18 \mathrm{~km} \mathrm{~h}^{-1}\). If all the kinetic energy of the man can be used to increase the temperature of water from \(20^{\circ} \mathrm{C}\) to \(30^{\circ} \mathrm{C}\), how much water can be heated with this energy?
CorrectIncorrectHint
Given
Mass of the man, \(m=50 \mathrm{~kg}\)
Speed of the man, \(v=18 \mathrm{~km} / \mathrm{h}=18 \times \frac{5}{18}=5 \mathrm{~m} / \mathrm{s}\)
Kinetic energy of the man is given by
\(
\begin{aligned}
& K=\frac{1}{2} m V^2 \\
& K=\left(\frac{1}{2}\right) 50 \times 5^2 \\
& K=25 \times 25=625 J
\end{aligned}
\)
Specific heat of the water, \(\mathrm{s}=4200 \mathrm{~J} / \mathrm{Kg}-K\)
Let the mass of the water heated be \(\mathrm{M}\).
The amount of heat required to raise the temperature of water from \(20^{\circ} \mathrm{C}\) to \(30^{\circ} \mathrm{C}\) is given by
\(
\begin{aligned}
& \mathrm{Q}=\mathrm{Ms} \Delta \mathrm{T}=\mathrm{M} \times 4200 \times(30-20) \\
& \mathrm{Q}=42000 \mathrm{M}
\end{aligned}
\)
According to the question,
\(
\begin{aligned}
& \mathrm{Q}=\mathrm{K} \\
& 42000 \mathrm{M}=625 \\
& \Rightarrow M=\frac{625}{42} \times 10^{-3} \\
& =14.88 \times 10^{-3} \mathrm{kg}\\
& =15 \mathrm{g}
\end{aligned}
\) -
Question 29 of 102
29. Question
A brick weighing \(4.0 \mathrm{~kg}\) is dropped into a \(1.0 \mathrm{~m}\) deep river from a height of \(2.0 \mathrm{~m}\). Assuming that \(80 \%\) of the gravitational potential energy is finally converted into thermal energy, find this thermal energy in calorie.
CorrectIncorrectHint
Given
Mass of the brick, \(m=4 \mathrm{~kg}\)
Total vertical distance travelled by the brick, \(h=3 \mathrm{~m}\)
Percentage of gravitational potential energy converted to thermal energy \(=80\)
Total change in potential energy of the brick \(=m g h=4 \times 10 \times 3=120 \mathrm{~J}\)
Thermal Energy \(=120 \times \frac{80}{100}=96 \mathrm{~J}\)
Thermal energy in calories is given by
\(
U=\frac{96}{4.2}=22.857 \mathrm{cal} \approx 23 \mathrm{cal}
\) -
Question 30 of 102
30. Question
A van of mass \(1500 \mathrm{~kg}\) travelling at a speed of \(54 \mathrm{~km} \mathrm{~h}^{-1}\) is stopped in \(10 \mathrm{~s}\). Assuming that all the mechanical energy lost appears as thermal energy in the brake mechanism, find the average rate of production of thermal energy in \(\mathrm{cal} \mathrm{s}^{-1}\).
CorrectIncorrectHint
Given
Mass of van, \(m=1500 \mathrm{~kg}\)
Speed of van, \(v=54 \mathrm{~km} / \mathrm{h}\)
\(
=54 \times\left(\frac{5}{18}\right)=15 \mathrm{~m} / \mathrm{s}
\)
Total kinetic energy of the van is given by
\(
\begin{aligned}
& K=\frac{1}{2} \mathrm{mv}^2 \\
& K=\frac{1}{2} \times 1500 \times(15)^2 \\
& \mathrm{~K}=750 \times 225 \\
& \mathrm{~K}=168750 \mathrm{~J} \\
& K=\frac{168750}{4.2} \\
& \mathrm{~K}=40178.57 \mathrm{cal}
\end{aligned}
\)
Loss in total energy of the van \(=40178 \mathrm{cal}\)
Loss in energy per second \(=\frac{40178}{10}=4017.8 \approx 4000 \mathrm{cal} . / \mathrm{sec}\)
\(\therefore\) Average rate of production of thermal energy \(\approx 4000 \mathrm{cal} / \mathrm{sec}\) -
Question 31 of 102
31. Question
A block of mass \(100 \mathrm{~g}\) slides on a rough horizontal surface. If the speed of the block decreases from \(10 \mathrm{~m} \mathrm{~s}{ }^{-1}\) to \(5 \mathrm{~m} \mathrm{~s}^{-1}\), find the thermal energy developed in the process.
CorrectIncorrectHint
Given
Mass of the block \(=100 \mathrm{~g}=0.1 \mathrm{~kg}\)
Initial speed of the block \(=10 \mathrm{~m} / \mathrm{s}\)
Final speed of the block \(=5 \mathrm{~m} / \mathrm{s}\)
Initial kinetic energy of the block \(=\frac{1}{2} \times 0.1 \times 10^2=5 J\)
Final kinetic energy of the block \(=\frac{1}{2} \times 0.1 \times 5^2=1.25 J\)
Change in kinetic energy of the block \(=5-1.25=3.75 \mathrm{~J}\)
Thermal energy developed is equal to the change in kinetic energy of the block. Thus,
Thermal energy developed in the process \(=3.75 \mathrm{~J}\) -
Question 32 of 102
32. Question
Two blocks of masses \(10 \mathrm{~kg}\) and \(20 \mathrm{~kg}\) moving at speeds of \(10 \mathrm{~m} \mathrm{~s}^{-1}\) and \(20 \mathrm{~m} \mathrm{~s}^{-1}\) respectively in opposite directions, approach each other and collide. If the collision is completely inelastic, find the thermal energy developed in the process.
CorrectIncorrectHint
Given
Mass of the first block, \(m_1=10 \mathrm{~kg}\)
Mass of the second block, \(\mathrm{m}_2=20 \mathrm{~kg}\)
Initial velocity of the first block, \(u_1=10 \mathrm{~m} / \mathrm{s}\)
Initial velocity of the second block, \(u_2=20 \mathrm{~m} / \mathrm{s}\)
Let the velocity of the blocks after collision be \(v\).
Applying conservation of momentum, we get
\(
\begin{aligned}
& m_2 u_2-m_1 u_1=\left(m_1+m_2\right) v \\
& \Rightarrow 20 \times 20-10 \times 10=(10+20) v \\
& \Rightarrow 400-100=30 v \\
& \Rightarrow 300=30 v \\
& \Rightarrow v=10 \mathrm{~m} / \mathrm{s}
\end{aligned}
\)
Initial kinetic energy is given by
\(
\begin{aligned}
& K_i=\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2 \\
& K_i=\frac{1}{2} \times 10 \times(10)^2+\frac{1}{2} \times 20 \times(20)^2 \\
& K_i=500+4000=4500
\end{aligned}
\)
Final kinetic energy is given by
\(
\begin{aligned}
& K_f=\frac{1}{2}\left(m_1+m_2\right) \mathrm{v}^2 \\
& K_f=\frac{1}{2}(10+20)(10)^2 \\
& K_f=\left(\frac{30}{2}\right) \times 100=1500
\end{aligned}
\)
\(\therefore\) Total change in \(\mathrm{KE}=4500 \mathrm{~J}-1500 \mathrm{~J}=3000 \mathrm{~J}\)
Thermal energy developed in the process \(=3000 \mathrm{~J}\) -
Question 33 of 102
33. Question
A ball is dropped on a floor from a height of \(2.0 \mathrm{~m}\). After the collision it rises up to a height of \(1.5 \mathrm{~m}\). Assume that \(40 \%\) of the mechanical energy lost goes as thermal energy into the ball. Calculate the rise in the temperature of the ball in the collision. Heat capacity of the ball is \(800 \mathrm{~J} \mathrm{~K}^{-1}\).
CorrectIncorrectHint
Height of the floor from which ball is dropped, \(h_1=2.0 \mathrm{~m}\)
Height to which the ball rises after collision, \(h_2=1.5 \mathrm{~m}\)
Let the mass of ball be \(\mathrm{m} \mathrm{kg}\).
Let the speed of the ball when it falls from \(h_1\) and \(h_2\) be \(v_1\) and \(v_2\), respectively.
\(
\begin{aligned}
& \nu_1=\sqrt{2 g h_1}=\sqrt{2 \times 10 \times 2}=\sqrt{40} \mathrm{~m} / \mathrm{s} \\
& \nu_2=\sqrt{2 g h_2}=\sqrt{2 \times 10 \times 1.5}=\sqrt{30} \mathrm{~m} / \mathrm{s}
\end{aligned}
\)
Change in kinetic energy is given by
\(
\begin{aligned}
& \Delta K=\frac{1}{2} \times m \times 40-\left(\frac{1}{2} m\right) \times 30=\left(\frac{10}{2}\right) m \\
& \Rightarrow \Delta K=5 \mathrm{~m}
\end{aligned}
\)
If the position of the ball is considered just before hitting the ground and after its first collision, then \(40 \%\) of the change in its KE will give the change in thermal energy of the ball. At these positions, the PE of the ball is same. Thus,
Loss in \(\mathrm{PE}=0\)
The change in kinetic energy is utilised in increasing the temperature of the ball.
Let the change in temperature be \(\Delta T\). Then,
\(
\begin{aligned}
& \left(\frac{40}{100}\right) \times \Delta K=m \times 800 \times \Delta T \\
& \left(\frac{40}{100}\right) \times \frac{10}{2} m=m \times 800 \times \Delta T \\
& \Rightarrow \Delta T=\frac{1}{400}=0.0025 \\
& =2.5 \times 10^{-3 \circ} C
\end{aligned}
\) -
Question 34 of 102
34. Question
A copper cube of mass \(200 \mathrm{~g}\) slides down on a rough inclined plane of inclination \(37^{\circ}\) at a constant speed. Assume that any loss in mechanical energy goes into the copper block as thermal energy. Find the increase in the temperature of the block as it slides down through \(60 \mathrm{~cm}\). Specific heat capacity of copper \(=420 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\).
CorrectIncorrectHint
Mass of copper cube, \(\mathrm{m}=200 \mathrm{~g}=0.2 \mathrm{~kg}\)
Length through which the block has slided, \(\mathrm{I}=60 \mathrm{~cm}=0.6 \mathrm{~m}\)
Since the block is moving with constant velocity, the net force on it is zero. Thus,
Force of friction, \(f=m g\)
Also, since the object is moving with a constant velocity, change in its K.E will be zero.As the object slides down, its PE decreases at the cost of increase in thermal energy of copper.The loss in mechanical energy of the copper block \(=\) Work done by the frictional force on the copper block to a distanceof \(60 \mathrm{~cm}\)
\(
\begin{aligned}
& W=m g l \sin \theta \\
& W=0.2 \times 10 \times 0.6 \sin 37^{\circ} \\
& W=1.2 \times\left(\frac{3}{5}\right)=0.72
\end{aligned}
\)
Let the change in temperature of the block be \(\Delta \mathrm{T}\).
Thermal energy gained by block \(=m s \Delta T=0.2 \times 420 \times \Delta T=84 \Delta T\)
But \(84 \Delta \mathrm{T}=0.72\)
\(
\begin{aligned}
& \Rightarrow \Delta T=\frac{0.72}{84}=0.00857 \\
& \Delta=0.0086=8.6 \times 10^{-3}{ }^{\circ} \mathrm{C}
\end{aligned}
\) -
Question 35 of 102
35. Question
A metal block of density \(6000 \mathrm{~kg} \mathrm{~m}^{-3}\) and mass \(1.2 \mathrm{~kg}\) is suspended through a spring of spring constant \(200 \mathrm{~N} \mathrm{~m}^{-1}\). The spring-block system is dipped in water kept in a vessel. The water has a mass of \(260 \mathrm{~g}\) and the block is at a height \(40 \mathrm{~cm}\) above the bottom of the vessel. If the support to the spring is broken, what will be the rise in the temperature of the water. Specific heat capacity of the block is \(250 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\) and that of water is \(4200 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\). Heat capacities of the vessel and the spring are negligible.
CorrectIncorrectHint
Given
Density of metal block, \(d=600 \mathrm{~kg} \mathrm{~m}^{-3}\)
Mass of metal block, \(\mathrm{m}=1.2 \mathrm{~kg}\)
Spring constant of the spring, \(k=200 \mathrm{~N} \mathrm{~m}^{-1}\)
Volume of the block, \(V=\frac{1.2}{6000}=2 \times 10^{-4} \mathrm{~m}^3\)
When the mass is dipped in water, it experiences a buoyant force and in the spring there is potential energy stored in it.
If the net force on the block is zero before breaking of the support of the spring, then
\(
\begin{aligned}
& \mathrm{kx}+\mathrm{V} \rho \mathrm{g}=\mathrm{mg} \\
& 200 \mathrm{x}+\left(2 \times 10^{-4}\right) \times(1000) \times(10)=12 \\
& \Rightarrow x=\frac{12-2}{200} \\
& \Rightarrow x=\frac{10}{200}=0.05 \mathrm{~m}
\end{aligned}
\)
The mechanical energy of the block is transferred to both block and water. Let the rise in temperature of the block and the water be \(\Delta T\).
Applying conservation of energy, we get
\(
\begin{aligned}
& \frac{1}{2} k x^2+m g h-V \rho g h=m_1 s_1 \Delta T+m_2 s_2 \Delta T \\
& \Rightarrow \frac{1}{2} \times 200 \times 0.0025+1.2 \times 10 \times\left(\frac{40}{100}\right)-2 \times 10^{-4} \times 1000 \times 10 \times\left(\frac{40}{100}\right) \\
& =\left(\frac{260}{1000}\right) \times 4200 \times \Delta T+1.2 \times 250 \times \Delta T \\
& \Rightarrow 0.25+4.8-0.8=1092 \Delta T+300 \Delta T \\
& \Rightarrow 1392 \Delta T=4.25 \\
& \Rightarrow \Delta T=\frac{4.25}{1392}=0.0030531 \\
& \Delta T=3 \times 10^{-3 \circ} \mathrm{C}
\end{aligned}
\) -
Question 36 of 102
36. Question
Does a gas have just two specific heat capacities or more than two? Is the number of specific heat capacities of agas countable?
CorrectIncorrectHint
No, a gas doesn’t have just two specific heat capacities, as the heat capacities depend on the process followed. There are infinite processes; therefore, there can be infinite number of specific heat capacities.
-
Question 37 of 102
37. Question
Can we define specific heat capacity at constant temperature?
CorrectIncorrectHint
Specific heat capacity, \(\mathrm{s}=\frac{\Delta \mathrm{Q}}{m \Delta T}\), where \(\frac{\Delta \mathrm{Q}}{m}\) is the heat supplied per unit mass of the substance and \(\Delta \mathrm{T}\) \(=0\); therefore, \(\mathrm{s}=\) infinity . So, we cannot define specific heat capacity at a constant temperature.
-
Question 38 of 102
38. Question
Can we define specific heat capacity for an adiabatic process?
CorrectIncorrectHint
Specific heat capacity, \(s=\frac{\Delta \mathrm{Q}}{m \Delta T}\), where \(\frac{\Delta \mathrm{Q}}{m}\) is the heat supplied per unit mass of the substance and \(\Delta \mathrm{T}\) is the change in temperature produced. In an adiabatic process, no heat exchange is allowed; so, \(\Delta Q=0\) and hence, \(s=0\). Therefore, in an adiabatic process, specific heat capacity is zero.
-
Question 39 of 102
39. Question
Does a solid also have two kinds of molar heat capacities \(C_p\) and \(C_V\)? If yes, do we have \(C_p>C_V\)? Is \(C_p-C_V=R\)?
CorrectIncorrectHint
Yes, a solid also has two kinds of molar heat capacities, \(C_p\) and \(C_{\mathrm{v}}\). In a solid, the expansion coefficient is quite small; therefore dependence of heat capacity on the process is negligible. So, \(C_p>C_v\) with just a small difference, which is not equal to \(R\).
-
Question 40 of 102
40. Question
In a real gas the internal energy depends on temperature and also on volume. The energy increases when the gas expands isothermally. Looking into the derivation of \(C_p-C_V=R\), find whether \(C_p-C_V\) will be more than \(R\), less than \(R\) or equal to \(\)R\(\) for a real gas.
CorrectIncorrectHint
In a real gas, as the internal energy depends on temperature and volume, the derived equation for an ideal gas
\((\mathrm{dQ})_{\mathrm{P}}=(\mathrm{dQ})_{\mathrm{V}}+\mathrm{nRdT}\) will change to
\((d Q)_P=(d Q)_V+n R d T+k\), where \(k\) is the change in internal energy (positive) due to change in volume when pressure is kept constant. So, in the case of a real gas, for \(n=1\) mole (say),
\(
\begin{aligned}
& C_P-C_V=R+\frac{k}{d t} \\
& \Rightarrow C_P-C_V>R
\end{aligned}
\)
where \(C_p\) and \(C_v\) are the specific heat capacities at constant pressure and volume, respectively. -
Question 41 of 102
41. Question
Can a process on an ideal gas be both adiabatic and isothermal?
CorrectIncorrectHint
According to the first law of thermodynamics, change in internal energy, \(\Delta \mathrm{U}\) is equal to the difference between heat supplied to the gas, \(\Delta \mathrm{Q}\) and the work done on the gas, \(\Delta \mathrm{W}\),
such that \(\Delta Q=\Delta U+\Delta W\). In an adiabatic process, \(\Delta Q=0\) and in an isothermal process, change in temperature, \(\Delta T=0\). Therefore,
\(
\begin{aligned}
& \Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W} \\
& \Rightarrow \Delta \mathrm{Q}=\mathrm{nC}_{\mathrm{v}} \Delta \mathrm{T}+\Delta \mathrm{W} \\
& \Rightarrow 0=\mathrm{nC}_{\mathrm{v}}(0)+\Delta \mathrm{W} \\
& \Rightarrow \Delta \mathrm{W}=0,
\end{aligned}
\)
if the process is adiabatic as well as isothermal, no work will be done. So, a process on an ideal gas cannot be both adiabatic and isothermal. -
Question 42 of 102
42. Question
The slope of p–V diagram is greater for an adiabatic process as compared to an isothermal process. Is this correct?
CorrectIncorrectHint
In an isothermal process,
\(
P V=k \quad \text {…(i) }
\)
On differentiating it w.r.t V, we get
\(
\begin{aligned}
& \mathrm{V} \frac{d P}{d V}+\mathrm{P}=0 \\
& \frac{d P}{d V}=-\frac{\mathrm{P}}{\mathrm{V}} \\
& \frac{d P}{d V}=-\frac{\mathrm{k}}{\mathrm{V}^2}[\text { Using (i)] }, \mathrm{k}=\text { constant }
\end{aligned}
\)
\(\mathrm{k}=\) constant
In an adiabatic process,
\(
P V^\gamma=K \ldots \text { (ii) }
\)
On differentiating it w.r.t V, we get
\(
\mathrm{V}^\gamma \frac{d \mathrm{P}}{d \mathrm{~V}}+\gamma \mathrm{PV}^{\gamma-1}=0
\)
\(\frac{d \mathrm{P}}{d \mathrm{~V}}=-\frac{\gamma \mathrm{PV}^{\gamma-1}}{\mathrm{~V}^{\gamma+1}}[\) Using \((i i), \gamma>1]\) and
\(\mathrm{K}\) is constant
\(\gamma\) and \(\frac{d \mathrm{P}}{d \mathrm{~V}}\)
are the slope of the curve and the ratio of heat capacities at constant pressure and volume, respectively; \(P\) is pressure and \(\mathrm{V}\) is volume of the system. By comparing the two slopes and keeping in mind that \(\gamma>1\), we can see that the slope of the \(P\)-V diagram is greater for an adiabatic process than an isothermal process. -
Question 43 of 102
43. Question
Is a slow process always isothermal? Is a quick process always adiabatic?
CorrectIncorrectHint
For an isothermal process, \(\mathrm{PV}=\mathrm{K}\), where \(\mathrm{P}\) is \(\mathrm{P}\) is pressure, \(\mathrm{V}\) is volume of the system and Kis constant. In an isothermal process, a small change in \(\mathrm{V}\) produces only a small change in \(\mathrm{p}\), so as to keep the product constant. On the other hand, in an adiabatic process, \(\mathrm{PV}^\gamma=\mathrm{k}, \gamma=\frac{\mathrm{C}_{\mathrm{p}}}{\mathrm{C}_{\mathrm{V}}}>1\)
is the ratio of heat capacities at constant pressure and volume, respectively, and \(\mathrm{k}\) is a constant. In this process, a small increase in volume produces a large decrease in pressure. Therefore, an isothermal process is considered to be a slow process and an adiabatic process a quick process. -
Question 44 of 102
44. Question
Can two states of an ideal gas be connected by an anisothermal process as well as an adiabatic process?
CorrectIncorrectHint
For two states to be connected by an isothermal process,
\(
P_1 V_1=P_2 V_2 \ldots \text { (i) }
\)
For the same two states to be connected by an adiabatic process,
\(
P_1 V_1{ }^\gamma=P_2 V_2{ }^\gamma \ldots \text { (ii) }
\)
If both the equations hold simultaneously then, on dividing equation (ii) by (i) we get
\(
V_1{ }^{\gamma-1}=V_2{ }^{\gamma-1}
\)
Let the gas be monatomic. Then,
\(
\begin{aligned}
& \gamma=\frac{5}{3} \\
& \Rightarrow \mathrm{V}_1^{\frac{2}{3}}=\mathrm{V}_2^{\frac{2}{3}} \\
& \Rightarrow \mathrm{V}_1=\mathrm{V}_2
\end{aligned}
\)
If this condition is met, then the two states can be connected by an isothermal as well as an adiabatic process. -
Question 45 of 102
45. Question
The ratio \(C_p / C_V\) for a gas is \(1.29\). What is the degree of freedom of the molecules of this gas?
CorrectIncorrectHint
For the molecules of a gas, \(\gamma=\frac{C_p}{C_V}=1+\frac{2}{f}\) where \({f}\) is the degree of freedom.
Given : \(\gamma=1.29\)
\(
\begin{aligned}
& \Rightarrow 1+\frac{2}{f}=1.29=\frac{9}{7} \\
& \Rightarrow \frac{2}{f}=\frac{9}{7}-1 \\
& \Rightarrow \frac{2}{f}=\frac{2}{7} \\
& \Rightarrow f=7
\end{aligned}
\)
Therefore, the molecules of this gas have 7 degrees of freedom.
But in reality, no gas can have more than 6 degrees of freedom. -
Question 46 of 102
46. Question
Work done by a sample of an ideal gas in a process \(A\) is double the work done in another process \(B\). The temperature rises through the same amount in the two processes. If \(C_A\) and \(C_B\) be the molar heat capacities for the two processes,
CorrectIncorrectHint
According to the first law of thermodynamics, \(\Delta Q=\Delta U+\Delta W\), where \(\Delta Q\) is the heat supplied to the system when \(\Delta \mathrm{W}\) work is done on the system and \(\Delta \mathrm{U}\) is the change in internal energy produced. Since the temperature rises by the same amount in both processes, change in internal energies are same, i.e. \(\Delta \mathrm{U}_{\mathrm{A}}=\) \(\Delta \mathrm{U}_{\mathrm{B}}\).
But as, \(\Delta \mathrm{W}_{\mathrm{A}}=\Delta \mathrm{W}_{\mathrm{B}}\) this gives \(\Delta \mathrm{Q}_{\mathrm{A}}=2 \Delta \mathrm{Q}_{\mathrm{B}}\).
Now, molar heat capacity of a gas, \(\mathrm{C}=\frac{\Delta Q}{n \Delta T}\), where \(\Delta \mathrm{Q} / \mathrm{n}\) is the heat supplied to a mole of gas and \(\Delta \mathrm{T}\) is the change in temperature produced. As \(\Delta \mathrm{Q}_{\mathrm{A}}=2 \Delta \mathrm{Q}_{\mathrm{B}}, \mathrm{C}_{\mathrm{A}}>\mathrm{C}_{\mathrm{B}}\). -
Question 47 of 102
47. Question
For a solid with a small expansion coefficient,
CorrectIncorrectHint
For a solid with a small expansion coefficient, work done in a process will also be small. Thus, the specific heat depends slightly on the process. Therefore, \(C_p\) is slightly greater than \(C_v\).
-
Question 48 of 102
48. Question
The value of \(C_p-C_V\) is \(1.00 \mathrm{R}\) for a gas sample in state \(A\) and is \(1.08 R\) in state \(B\). Let \(p_A, p_B\) denote the pressures and \(T_A\) and \(T_B\) denote the temperatures of the states \(A\) and \(B\) respectively. Most likely
CorrectIncorrectHint
\(C_p-C_v=R\) for the gas in state \(A\), which means it is acting as an ideal gas in that state, whereas \(C_p-C_v=\)
\(1.08 \mathrm{R}\) in state B, i.e. the behaviour of the gas is that of a real gas in that state. To be an ideal gas, a real gas at STP should be at a very high temperature and low pressure.Therefore, \(\mathrm{P}_{\mathrm{A}}<\mathrm{P}_{\mathrm{B}}\) and \(\mathrm{T}_{\mathrm{A}}>\mathrm{T}_{\mathrm{B}}\) where \(\mathrm{P}_{\mathrm{A}}\) and \(\mathrm{P}_{\mathrm{B}}\) denotes the pressure and \(\mathrm{T}_{\mathrm{A}}\) and \(\mathrm{T}_{\mathrm{B}}\) denotes the temperature of system A and B reepectively.
-
Question 49 of 102
49. Question
Let \(C_V\) and \(C_p\) denote the molar heat capacities of an ideal gas at constant volume and constant pressure respectively. Which of the following is a universal constant?
CorrectIncorrectHint
For an ideal gas, \(C_p-C_v=R\), where \(C_v\) and \(C_p\) denote the molar heat capacities of an ideal gas at constant volume and constant pressure, respectively and \(\mathrm{R}\) is the gas constant whos value is \(8.314 \mathrm{~J} / \mathrm{K}\).
Therefore, \(C_p-C_v\) is a constant. On the other hand, the ratio of these two varies as the atomicity of the gas changes. Also, their sum and product are not constant. -
Question 50 of 102
50. Question
70 calories of heat is required to raise the temperature of 2 mole of an ideal gas at constant pressure from \(30^{\circ} \mathrm{C}\) to \(35^{\circ} \mathrm{C}\). The amount of heat required to raise the temperature of the same gas through the same range at constant volume is
CorrectIncorrectHint
It is given that 70 calories of heat are required to raise the temperature of 2 mole of an ideal gas at constant pressure from \(30^{\circ} \mathrm{C}\) to \(35^{\circ} \mathrm{C}\). Also, specific heat at constant pressure,
\(
\begin{aligned}
& C_p=\frac{\Delta Q}{n \Delta T} \\
& \Rightarrow C_p=\frac{70}{2 \times(35-30)} \\
& \Rightarrow C_p=\frac{70}{2 \times 5} \\
& \Rightarrow C_p=7 \text { calories }-\mathrm{mol}^{-1} \mathrm{~K}^{-1}
\end{aligned}
\)
For an ideal gas,
\(
\begin{aligned}
& C_P-C_V=R=8.314 \mathrm{~J}-\mathrm{mol}^{-1} \mathrm{~K}^{-1} \simeq 2 \text { calories } \mathrm{mol}^{-1} \mathrm{~K}^{-1} \\
& \Rightarrow C_V=C_P-R \\
& \Rightarrow C_V=(7-2) \text { calories }-\mathrm{mol}^{-1} \mathrm{~K}^{-1} \\
& \Rightarrow C_V=5 \text { calories }-\mathrm{mol}^{-1} \mathrm{~K}^{-1}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow C_{\mathrm{V}}=\frac{\Delta \mathrm{Q}}{n \Delta \mathrm{T}} \\
& \Rightarrow 5=\frac{\Delta \mathrm{Q}}{2 \times(35-30)} \\
& \Rightarrow \Delta \mathrm{Q}=5 \times 2 \times(35-30) \\
& \Rightarrow \Delta \mathrm{Q}=5 \times 2 \times 5 \\
& \Rightarrow \Delta \mathrm{Q}=50 \text { calories }
\end{aligned}
\)
Therefore, 50 calories need to be supplied to raise the temperature of 2 moles of gas from \(30-35^{\circ} \mathrm{C}\) at constant volume. -
Question 51 of 102
51. Question
The figure below shows a process on a gas in which pressure and volume both change. The molar heat capacity for this process is \(C\).
 CorrectIncorrect
CorrectIncorrectHint
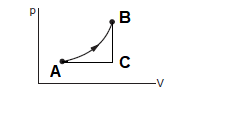
Consider two processes \(A B\) and \(A C B\); let \(W\) be the work done. \(C\) is the molar heat capacity of process \(A B\). Process ACB can be considered as the sum of the two processes, AC and CB. The molar heat capacity of process \(A C\) is \(C_p\), as pressure is constant in this process and the molar heat capacity of process \(C B\) is \(C_v\), as volume is constant in it.
Internal energy, U, is a state function, i.e. it doesn’t depend on the path followed. Therefore,
\(
\begin{aligned}
& \mathrm{U}_{\mathrm{AB}}=\mathrm{U}_{\mathrm{ACB}} \\
& \mathrm{W}_{\mathrm{AB}}>\mathrm{W}_{\mathrm{ACB}}
\end{aligned}
\)
Work done in the \(p-V\) diagram is the area enclosed under the curve.
\(
\begin{aligned}
& \Rightarrow W_{A B}+U_{A B}>W_{A C B}+U_{A C B} \\
& \Rightarrow C>C_V+C_P
\end{aligned}
\)
Molar heat capacity is the heat supplied per mole to change the temperature by a degree Kelvin and according to the first law of thermodynamics, \(d Q=d U+d W\), where \(d Q\) is the heat supplied to the system in a process.
\(
\Rightarrow C>C_V
\) -
Question 52 of 102
52. Question
The molar heat capacity for the process shown in the figure below is
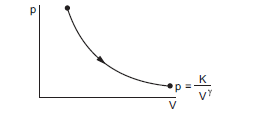 CorrectIncorrect
CorrectIncorrectHint
\(
\begin{aligned}
& p=\frac{k}{V^g} \\
& \Rightarrow p{V^g}=k
\end{aligned}
\)
such that the process is adiabatic in which there’s no heat supplied to the system, i.e. \(Q=0\). Molar heat capacity is the amount of heat supplied to the system per mole to produce a degree change in temperature.
Also, in an adiabatic process, no heat exchange is allowed. So, molar heat capacity equals zero, i.e. \(C=0\). -
Question 53 of 102
53. Question
In an isothermal process on an ideal gas, the pressure increases by \(0.5 \%\). The volume decreases by about
CorrectIncorrectHint
Let \(p\) and \(p^{\prime}\) be the initial and final pressures of the system and \(V\) and \(V^{\prime}\) be the initial and final volumes of the system. \(p^{\prime}\) is \(0.5 \%\) more than \(p\) and the process is isothernal. So, \(p V=k=p^{\prime} V^{\prime}=\) constant. Therefore,
\(
\begin{aligned}
& \mathrm{p}{\mathrm{V}}=\mathrm{p}^{\prime} \mathrm{V}^{\prime} \\
& \Rightarrow \mathrm{p}{\mathrm{V}}=\left(\mathrm{p}+\frac{0.5}{100} \mathrm{p}\right) \mathrm{V}^{\prime} \\
& \Rightarrow \mathrm{p}{\mathrm{V}}=\frac{100.5}{100} \mathrm{p}{\mathrm{V}^{\prime}} \\
& \Rightarrow \mathrm{V}^{\prime}=\frac{100}{100.5} \mathrm{~V} \\
& \Rightarrow \mathrm{V}^{\prime}-\mathrm{V}=\frac{100}{100.5} \mathrm{~V}-\mathrm{V} \\
& =-\frac{0.5}{100.5} \\
& =-0.49 \%
\end{aligned}
\)
So, volume V’ decreases by about \(0.5 \%\) of \(\mathrm{V}\). -
Question 54 of 102
54. Question
In an adiabatic process on a gas with \(\gamma=1.4\), the pressure is increased by \(0.5 \%\). The volume decreases by about
CorrectIncorrectHint
For adiabatic process
\(
\begin{aligned}
& \mathrm{PV}^{\gamma}=\mathrm{k} \\
& \mathrm{p}=\mathrm{kv}^{-\gamma} \\
& \Rightarrow \frac{\mathrm{dp}}{\mathrm{p}}=-\gamma \frac{(\mathrm{dv})}{\mathrm{v}} \\
& \Rightarrow \frac{\mathrm{dv}}{\mathrm{v}}=-\frac{1}{\gamma} \frac{\mathrm{dp}}{\mathrm{p}} \\
& \Rightarrow \frac{\mathrm{dv}}{\mathrm{v}}=-\frac{1}{\gamma} \times \%\left(\frac{\mathrm{dp}}{\mathrm{p}}\right) \\
& =-\frac{1}{1.4} \times(0.5) \\
& =-\frac{1}{2.8} \%=-0.36 \%
\end{aligned}
\) -
Question 55 of 102
55. Question
Two samples \(A\) and \(B\) are initially kept in the same state. The sample \(A\) is expanded through an adiabatic process and the sample \(B\) through an isothermal process. The final volumes of the samples are the same. The final pressures in \(A\) and \(B\) are \(p_A\) and \(p_B\) respectively.
CorrectIncorrectHint
Let the initial states of samples \(A\) and \(B\) be \(i\) and the final states of samples B and A be f and \(f^{\prime}\), respectively. Let the final volumes of both be \(V_0\). As sample \(A\) is expanded through an adiabatic process, its curve in the \(\mathrm{p}-\mathrm{V}\) diagram is steeper than that of sample B, which is expanded through an isothermal process. Therefore, from the \(\mathrm{p}-\mathrm{V}\) diagram, \(\mathrm{p}_{\mathrm{A}}<\mathrm{p}_{\mathrm{B}}\).
-
Question 56 of 102
56. Question
Let \(T_a\) and \(T_b\) be the final temperatures of the samples \(A\) and \(B\) respectively in the previous question.
CorrectIncorrectHint
As sample B is undergoing expansion through an isothermal process, its initial and final temperatures will be same, i.e. \(T_b\). On the other hand, sample \(A\) is at the same initial state as B, such that the initial temperature of \(A\) is \(T_b\) and it is expanding through an adiabatic process in which no heat is supplied. Therefore, sample A will expand at the cost of its internal energy and its final temperature will be less than its initial temperature. This implies that \(T_a<T_b\).
-
Question 57 of 102
57. Question
Let \(\Delta W_a\) and \(\Delta W_b\) be the work done by the systems \(A\) and \(B\) respectively in the previous question.
CorrectIncorrectHint

In the \(p-V\) diagram, the area under the curve w.r.t the \(V\) axis is equal to the work done by the system. Since the area under the isotherm is greater than that under the adiabat, the work done by the system \(\mathrm{A}\) is less than that done by the system \(\mathrm{B}\). Hence, \(\Delta \mathrm{W}_{\mathrm{a}}<\Delta \mathrm{W}_{\mathrm{b}}\).
-
Question 58 of 102
58. Question
The molar heat capacity of oxygen gas at STP is nearly \(2 \cdot 5 R\). As the temperature is increased, it gradually increases and approaches \(3.5 R\). The most appropriate reason for this behaviour is that at high temperatures
CorrectIncorrectHint
Molar-specific heat capacity has a direct dependence on the degree of freedom of gas molecules. As the temperature is increased, the gas molecules start vibrating about their mean position, leading to a change (increase) in the degree of freedom and, hence, increasing molar heat capacity.
-
Question 59 of 102
59. Question
A gas kept in a container of finite conductivity is suddenly compressed. The process
CorrectIncorrectHint
(c) may be very nearly adiabatic
(d) may be very nearly isothermal
Due to sudden compression, the gas did not get sufficient time for heat exchange. So, no heat exchange occurred. Therefore, the process may be adiabatic. For any process to be isothermal, its temperature should remain constant, i.e. pressure and volume should change simultaneously while their product (temperature) should be constant. -
Question 60 of 102
60. Question
Let \(Q\) and \(W\) denote the amount of heat given to an ideal gas and the work done by it in an isothermal process.
CorrectIncorrectHint
In an isothermal process, temperature of the system stays constant, i.e. there’s no change in internal energy. Thus, \(U=0\), where \(U\) denotes the change in internal energy of the system. According to the first law of thermodynamics, heat supplied to the system is equal to the sum of change in internal energy and work done by the system, such that \(Q=U+W\). As \(U=0, Q=W\).
-
Question 61 of 102
61. Question
Let \(Q\) and \(W\) denote the amount of heat given to an ideal gas and the work done by it in an adiabatic process.
CorrectIncorrectHint
(a) \(Q=0\)
(d) \(Q \neq W\)
In an adiabatic process, no heat is supplied to the system; so, \(Q=0\). According to the first law of thermodynamics, heat given to any system is equal to the sum of the change in internal energy and the work done on the system. So, \(Q=W+U\) and as \(Q=0, W=-U\) and \(Q \neq W\). -
Question 62 of 102
62. Question
Consider the processes A and B shown in the figure below.It is possible that
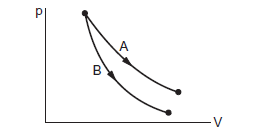 CorrectIncorrect
CorrectIncorrectHint
The slope of an adiabatic process is greater than that of an isothermal process. Since Aand B are initiated from the same initial state, both cannot be isothermal or adiabatic, as they would be overlapping. But the curve of process B is steeper than the curve of process A. Hence, A is isothermal and B is adiabatic.
-
Question 63 of 102
63. Question
Three identical adiabatic containers A, B, and C contain helium, neon, and oxygen respectively at equal pressure. The gases are pushed to half their original volumes.
CorrectIncorrectHint
((c) The pressures of helium and neon will be the same but that of oxygen will be different.
(d) The temperatures of helium and neon will be the same but that of oxygen will be different.
Adiabatic process is expressed as
\(p{V}^{\gamma}=\) constant or
\(T{V}^{\gamma-1}=\) constant
where \(\gamma=\frac{C^p}{C^v}\)
is the ratio of molar heat capacities at constant pressure and volume.
We know that \(\gamma\) is equal to \(1.67\) and \(1.40\) for a monatomic gas and a diatomic gas, respectively. Helium and neon are monatomic gases and oxygen is a diatomic gas. Therefore, changing the state of the gases, i.e. reducing the volume will lead to identical changes in temperature and pressure for helium and neon and that will be different for oxygen. -
Question 64 of 102
64. Question
A rigid container of negligible heat capacity contains one mole of an ideal gas. The temperature of the gas increases by \(1^{\circ} \mathrm{C}\) if \(3.0 \mathrm{cal}\) of heat is added to it. The gas may be
CorrectIncorrectHint
(a) helium
(b) argon
The temperature of one mole of a gas kept in a container of fixed volume is increased by 1 degree Celsius if 3 calories, i.e. \(12.54 \mathrm{~J}\) of heat is added to it. So, its molar heat capacity, \(C_{\mathrm{V}}=12.54 \mathrm{~J} \mathrm{JK}^{-1} \mathrm{~mol}^{-1}\), as molar heat capacity at fixed volume is the heat supplied to a mole of gas to increase its temperature by a degree. For a monatomic gas, \(\mathrm{C}_{\mathrm{v}} \simeq \frac{3}{2} \mathrm{R}=1.5 \times 8.314=12.54 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}\). Among the given gases, only helium and argon are inert and, hence, monoatomic. Therefore, the gas may be helium or argon. -
Question 65 of 102
65. Question
Four cylinders contain equal number of moles of argon, hydrogen, nitrogen, and carbon dioxide at the same temperature. The energy is minimum in
CorrectIncorrectHint
The energy of a gas is measured as \(\mathrm{C}_{\mathrm{v}} \mathrm{T}\). All the four cylinders are at the same temperature but the gases in them have different values of \(C_v\), such that it is least for the monatomic gas and keeps on increasing as we go from monatomic to tri-atomic. Among the above gases, argon is monatomic, hydrogen and nitrogen are diatomic and carbon dioxide is tri-atomic. Therefore, the energy is minimum in argon.
-
Question 66 of 102
66. Question
A vessel containing one mole of a monatomic ideal gas (molecular weight \(=20 \mathrm{~g} \mathrm{~mol}^{-1}\) ) is moving on a floor at a speed of \(50 \mathrm{~m} \mathrm{~s}^{-1}\). The vessel is stopped suddenly. Assuming that the mechanical energy lost has gone into the internal energy of the gas, find the rise in its temperature.
CorrectIncorrectHint
Number of moles of the ideal gas, \(n=1\) mole
Molecular weight of the gas, \(W=20 \mathrm{~g} / \mathrm{mole}\)
Mass of the gas, \(m=20 \mathrm{~g}\)
Velocity of the vessel, \(V=50 \mathrm{~m} / \mathrm{s}\)
Decrease in K.E. of the vessel = Internal energy gained by the gas
\(
\begin{aligned}
& \mathrm{KE}=\frac{1}{2} m\left(u^2-v^2\right) \\
& \mathrm{KE}=\frac{1}{2} \times 20 \times 10^{-3} \times(0-50 \times 50)
\end{aligned}
\)
\(\mathrm{KE}=-25 \mathrm{~J}=\) gain in internal energy of the gas change in internal energy of a gas \(\frac{d}{2} n R(\triangle \mathrm{T})\) where \(d\) is the degree of freedom of the gas \(F\) or a monoatomic gas, \(d=3\).
\(
\begin{aligned}
& \text { So, } 25=\frac{3}{2} n R(\triangle T) \\
& \Rightarrow 25=1 \times \frac{3}{2} \times 8.31 \times \Delta T \\
& \Rightarrow \triangle T=\frac{50}{3 \times 8.3}=2 \mathrm{~K}
\end{aligned}
\) -
Question 67 of 102
67. Question
\(5 \mathrm{~g}\) of a gas is contained in a rigid container and is heated from \(15^{\circ} \mathrm{C}\) to \(25^{\circ} \mathrm{C}\). Specific heat capacity of the gas at constant volume is \(0.172 \mathrm{cal} \mathrm{g}^{-1}{ }^{\circ} \mathrm{C}^{-1}\) and the mechanical equivalent of heat is \(4 \cdot 2 \mathrm{~J} \mathrm{cal}^{-1}\). Calculate the change in the internal energy of the gas.
CorrectIncorrectHint
Given:
Mass of the gas, \(m=5 \mathrm{~g}\)
Change in temperature of the system, \(\Delta \mathrm{T}=25-15^{\circ} \mathrm{C}=10^{\circ} \mathrm{C}\)
Specific heat at constant volume, \(C_v=0.172 \mathrm{cal} / \mathrm{g}{ }^{\circ} \mathrm{C}\)
Mechanical equivalent, \(\mathrm{J}=4.2 \mathrm{~J} / \mathrm{cal}\)
From the first law of thermodynamics,
\(
\mathrm{dQ}=\mathrm{dU}+\mathrm{dW}
\)
Now ,
\(\Delta \mathrm{V}=0\) (Rigid wall of the container keeps the volume constant)
So, \(\mathrm{dW}=\mathrm{P} \Delta \mathrm{V}=0\)
Therefore,
\(\mathrm{dQ}=\mathrm{dU}\) (From the first law)
\(
\begin{aligned}
& \mathrm{Q}=\mathrm{mc}_{\mathrm{v}} \mathrm{dT}=5 \times 0.172 \times 10 \\
& =8.6 \mathrm{cal}=8.6 \times 4.2 \mathrm{~J} \\
& =36.12 \mathrm{~J}
\end{aligned}
\)
So, the change in internal energy of the system is \(36 \mathrm{~J}\). -
Question 68 of 102
68. Question
Figure below shows a cylindrical container containing oxygen \((\gamma=1 \cdot 4)\) and closed by a \(50 \mathrm{~kg}\) frictionless piston. The area of cross section is \(100 \mathrm{~cm}^2\), atmospheric pressure is \(100 \mathrm{kPa}\) and \(g\) is \(10 \mathrm{~m} \mathrm{~s}^{-2}\). The cylinder is slowly heated for some time. Find the amount of heat supplied to the gas if the piston moves out through a distance of \(20 \mathrm{~cm}\).
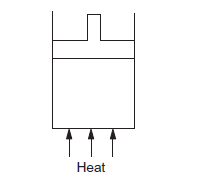 CorrectIncorrect
CorrectIncorrectHint
Given:
Mass of the piston \((\mathrm{m})=50 \mathrm{~kg}\)
Adiabatic constant of the gas, \(\gamma=1.4\)
Area of cross-section of the piston \((A)=100 \mathrm{~cm}^2\)
Atmospheric pressure \(\left(P_0\right)=100 \mathrm{kPa}\)
\(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2\)
Distance moved by the piston, \(x=20 \mathrm{~cm}\)
Work done by the gas,
\(d W=P d v\)
The pressure \((p)\) is because of two factors : the first is the initial pressure and
Therefore,
Therefore,
\(
\begin{aligned}
& \mathrm{W}=\left(\frac{\mathrm{mg}}{\mathrm{A}}+\mathrm{P}_0\right) \times \mathrm{Ad} x \\
& \mathrm{~W}=\left(\frac{50 \times 10}{100 \times 10^{-4}}+10_5\right) \times 100 \times 10^{-4} \times 20 \times 10^{-4} \\
& \mathrm{~W}=\left(5 \times 10^4+10^5\right) \times 20 \times 10^{-4} \\
& \mathrm{~W}=1.5 \times 10^5 \times 20 \times 10^{-4} \\
& \mathrm{~W}=300 \mathrm{~J} \\
& \text { Hence, } \mathrm{nRdT}=\mathrm{P} \Delta \mathrm{V}=300 \\
& \Rightarrow \mathrm{dT}=\frac{300}{\mathrm{nR}} \\
& \text { So, dQ }=\mathrm{nC_p} \mathrm{dT}=\mathrm{nC_p} \times\left(\frac{300}{\mathrm{nR}}\right) \\
& \text { Using } C_p-C_{\mathrm{v}}=\mathrm{R} \text { and } \frac{C_p}{C_{\mathrm{v}}}=\gamma \\
& \text { dQ }=\frac{\mathrm{n} \gamma \mathrm{R} 300}{(\gamma-1) \mathrm{nR}} \\
& \mathrm{dQ}=\left(\frac{300 \times 1.4}{0.4}\right)=1050 \mathrm{~J}
\end{aligned}
\) -
Question 69 of 102
69. Question
The specific heat capacities of hydrogen at constant volume and at constant pressure are \(2.4 \mathrm{cal} \mathrm{g}^{-1}{ }^{\circ} \mathrm{C}^{-1}\) of hydrogen is \(2 \mathrm{~g} \mathrm{~mol}^{-1}\) and the gas constant \(R=8.3 \times 10^7 \mathrm{erg}^{\circ} \mathrm{C}^{-1} \mathrm{~mol}^{-1}\). Calculate the value of \(J\).
CorrectIncorrectHint
Specific heat capacity at constant volume, \(\mathrm{C}_{\mathrm{v}}\left(\mathrm{H}_2\right)=2.4 \mathrm{cal} / \mathrm{g}-{ }^{\circ} \mathrm{C}\)
Specific heat capacity at constant pressure, \(\mathrm{C}_{\mathrm{p}}\left(\mathrm{H}_2\right)=3.4 \mathrm{cal} / \mathrm{g}-{ }^{\circ} \mathrm{C}\)
Molecular weight, \(M=2 \mathrm{~g} / \mathrm{mol}\)
Gas constant, \(R=8.3 \times 10^7 \mathrm{erg} / \mathrm{mol}-^{\circ} \mathrm{C}\)
We know: \(C_p-C_v=1 \mathrm{cal} / \mathrm{g}-{ }^{\circ} \mathrm{C}\),
where \(C_p\) and \(C_v\) are molar specific heat capacities.
So, difference of molar specific heat,
\(
C_p \times M-C_v \times M=1 \mathrm{cal} / \mathrm{mol}^{-}{ }^{\circ} \mathrm{C}
\)
Now, \(2 \times J=R\)
\(
\begin{aligned}
& \Rightarrow 2 \times J=8.3 \times 10^7 \mathrm{erg} / \mathrm{mol}{ }^{\circ} \mathrm{C} \\
& \Rightarrow J=4.15 \times 10^7 \mathrm{erg} / \mathrm{cal}
\end{aligned}
\) -
Question 70 of 102
70. Question
The ratio of the molar heat capacities of an ideal gas is \(C_p / C_V=7 / 6\). Calculate the change in internal energy of \(1.0\) mole of the gas when its temperature is raised by \(50 \mathrm{~K}\) (a) keeping the pressure constant, (b) keeping the volume constant and (c) adiabatically.
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{\mathrm{C}_{\mathrm{P}}}{\mathrm{C}_{\mathrm{V}}}=7.6, \mathrm{n}=1 \text { mole, } \quad \Delta \mathrm{T}=50 \mathrm{~K} \\
& \text { (a) Keeping the pressure constant, dQ }=\mathrm{du}+\mathrm{dW}, \\
& \begin{aligned}
& \Delta T=50 \mathrm{~K}, \quad \gamma=7 / 6, \mathrm{~m}=1 \mathrm{~mole}, \\
& \mathrm{dQ}=\mathrm{du}+\mathrm{dw} \Rightarrow \mathrm{nC_v} \mathrm{dT}=\mathrm{du}+\mathrm{RdT} \Rightarrow \mathrm{du}=\mathrm{nC_p dT}-\mathrm{RdT} \\
&= 1 \times \frac{\mathrm{R} \gamma}{\gamma-1} \times \mathrm{dT}-\mathrm{RdT}=\frac{\mathrm{R} \times \frac{7}{6}}{\frac{7}{6}-1} \mathrm{dT}-\mathrm{RdT}
\end{aligned} \\
& =\mathrm{DT}-\mathrm{RdT}=7 \mathrm{RdT}-\mathrm{RdT}=6 \mathrm{RdT}=6 \times 8.3 \times 50=2490 \mathrm{~J}.
\end{aligned}
\)
(b) Kipping Volume constant, dv \(=n C_V d T\)
\(
\begin{aligned}
& =1 \times \frac{\mathrm{R}}{\gamma-1} \times \mathrm{dt}=\frac{1 \times 8.3}{\frac{7}{6}-1} \times 50 \\
& =8.3 \times 50 \times 6=2490 \mathrm{~J}
\end{aligned}
\)
(c) Adiabetically \(d Q=0, \quad d u=-d w\)
\(
=\left[\frac{n \times R}{\gamma-1}\left(T_1-T_2\right)\right]=\frac{1 \times 8.3}{\frac{7}{6}-1}\left(T_2-T_1\right)=8.3 \times 50 \times 6=2490 \mathrm{~J}
\) -
Question 71 of 102
71. Question
A sample of air weighing \(1.18 \mathrm{~g}\) occupies \(1.0 \times 10^3 \mathrm{~cm}^3\) when kept at \(300 \mathrm{~K}\) and \(1.0 \times 10^5 \mathrm{~Pa}\). When \(2.0 \mathrm{cal}\) of heat is added to it at constant volume, its temperature increases by \(1^{\circ} \mathrm{C}\). Calculate the amount of heat needed to increase the temperature of air by \(1^{\circ} \mathrm{C}\) at constant pressure if the mechanical equivalent of heat is \(4.2 \times 10^{-7} \mathrm{erg} \mathrm{cal}^{-1}\). Assume that air behaves as an ideal gas.
CorrectIncorrectHint
\(
\begin{aligned}
& m=1.18 g \\
& V=1 \times 10^3 \mathrm{~cm}^3=1 L \\
& T=300 K, P=10^5 \mathrm{~Pa} \\
& P V=n R T \\
& \text { ог } n=\frac{P V}{R T}\left[10^5 \mathrm{~Pa}=1 \mathrm{~atm} .\right] \\
& \text { implies } n=\frac{1}{8.2 \times 10^{-2} \times 3 \times 10^2} \\
& =\frac{1}{8.2 \times 3}=\frac{1}{24.6} \\
& \text { Now, } C_v=\frac{1}{n} \times 2=24.6 \times 2=49.2 \\
& C_p=R+C_v=1.987+49.2 \\
& =51.187 \\
& Q=n C_p d T \\
& =\frac{1}{24.6} \times 51.187 \times 1 \\
& =2.08 \mathrm{cal}
\end{aligned}
\) -
Question 72 of 102
72. Question
An ideal gas expands from \(100 \mathrm{~cm}^3\) to \(200 \mathrm{~cm}^3\) at a constant pressure of \(2.0 \times 10^5 \mathrm{~Pa}\) when \(50 \mathrm{~J}\) of heat is supplied to it. Calculate (a) the change in internal energy of the gas, (b) the number of moles in the gas if the initial temperature is \(300 \mathrm{~K}\), (c) the molar heat capacity \(C_p\) at constant pressure and (d) the molar heat capacity \(C_V\) at constant volume.
CorrectIncorrectHint
\(
\mathrm{V}_1=100 \mathrm{~cm}^3, \mathrm{~V}_2=200 \mathrm{~cm}^3, \mathrm{P}=2 \times 10^5 \mathrm{~Pa}, \Delta \mathrm{Q}=50 \mathrm{~J}
\)
(a) \(\Delta Q=d u+d w=>50=d u+20 \times 10^5\left(200-100 \times 10^{-6}\right) \Rightarrow 50=d u+20 \Rightarrow>d u=30 \mathrm{~J}\)
(b) \(30=n \times \frac{3}{2} \times 8.3 \times 300\left[U=\frac{3}{2} n R T\right.\) for monoatomic \(]\)
\(
\Rightarrow \mathrm{n}=\frac{2}{3 \times 83}=\frac{2}{249}=0.008
\)
(c) \(\mathrm{du}=\mathrm{nC}_{\mathrm{v}} \mathrm{dT} \Rightarrow \mathrm{C}_{\mathrm{v}}=\frac{\text { dndTu }}{}=\frac{30}{0.008 \times 300}=12.5\)
\(
C_p=C_v+R=12.5+8.3=20.8 \mathrm{J} \mathrm{K}^{-1} \mathrm{~mol}^{-1}
\)
(d) \(C_v=12.5\) \(\mathrm{J} \mathrm{K}^{-1} \mathrm{~mol}^{-1}\)(Proved above) -
Question 73 of 102
73. Question
An amount \(Q\) of heat is added to a monatomic ideal gas in a process in which the gas performs a work \(Q / 2\) on its surrounding. Find the molar heat capacity for the process.
CorrectIncorrectHint
Given:
Amount of heat given to the gas \(=Q\)
So, \(\Delta \mathrm{Q}=\mathrm{Q}\)
Work done by the gas, \(\Delta \mathrm{W}=\frac{Q}{2}\)
From the first law of thermodynamics,
\(
\begin{aligned}
& \Delta \mathrm{Q}=\Delta \mathrm{W}+\Delta \mathrm{U} \\
& \Rightarrow \Delta \mathrm{U}=\mathrm{Q}-\frac{\mathrm{Q}}{2}=\frac{\mathrm{Q}}{2}
\end{aligned}
\)
For a monoatomic gas,
\(
\begin{aligned}
& \Delta \mathrm{U}=\frac{3}{2} n \mathrm{RdT} \\
& \Rightarrow \frac{\mathrm{Q}}{2}=\mathrm{ndT} \times \frac{3}{2} \mathrm{R} \\
& \Rightarrow \mathrm{Q}=3 \mathrm{nRdT}
\end{aligned}
\)
Again, for expansion at constant pressure,
\(
\mathrm{Q}=\mathrm{nC}_{\mathrm{p}} \mathrm{dT} \text {, }
\)
where \(C_p\) is the molar heat capacity at constant pressure.
So, \(3 \mathrm{nRdT}=n C_p d T\)
\(
\Rightarrow C_p=3 R
\) -
Question 74 of 102
74. Question
An ideal gas is taken through a process in which the pressure and the volume are changed according to the equation \(\)p=k V\(\). Calculate the molar heat capacity of the gas for the process.
CorrectIncorrectHint
Relation between pressure and volume of a gas is \(P=\mathrm{kV}\).
Ideal gas equation is \(P V=n R T\).
\(
\begin{aligned}
& \Rightarrow \frac{\mathrm{nRT}}{\mathrm{V}}=\mathrm{kV} \\
& \Rightarrow \mathrm{nRT}=\mathrm{kV}^2
\end{aligned}
\)
For simplicity, take the number of moles of a gas, \(n=1\).
\(
\begin{aligned}
& \Rightarrow \mathrm{RdT}=2 \mathrm{kVdV} \\
& \Rightarrow \frac{\mathrm{RdT}}{2 \mathrm{kV}}=\mathrm{dV}
\end{aligned}
\)
From the first law of thermodynamics,
\(
\begin{aligned}
& d Q=d U+d W \\
& \Rightarrow n C_p d T=C_V d T+P d V \\
& \Rightarrow n C_p d T=C_v d T+\frac{P R d T}{2 k V} \\
& \Rightarrow 1 \times C_p=C_v+\frac{P R}{2 k v} \\
& \therefore C_p=C_v+\frac{R}{2}
\end{aligned}
\) -
Question 75 of 102
75. Question
An ideal gas \(\left(C_p / C_V=\gamma\right)\) is taken through a process in which the pressure and the volume vary as \(p=a V^b\). Find the value of \(b\) for which the specific heat capacity in the process is zero.
CorrectIncorrectHint
As the process has specific heat capacity zero, the process is essentially an adiabatic process.
For an adiabatic process
\(
\begin{aligned}
& \mathrm{PV}^\gamma=\mathrm{c} \\
& \Rightarrow \mathrm{P}=\frac{\mathrm{c}}{\mathrm{V}^\gamma}=\mathrm{cV}^{-\gamma}
\end{aligned}
\)
Comparing with eqn.
\(
\begin{aligned}
& P=a V^b \\
& \Rightarrow a=c \\
& \Rightarrow b=-\gamma
\end{aligned}
\) -
Question 76 of 102
76. Question
Two ideal gases have the same value of \(C_p / C_V=\gamma\). What will be the value of this ratio for a mixture of the two gases in the ratio \(1: 2\)?
CorrectIncorrectHint
Let the heat capacities be \(\mathrm{C}_P\) and \(\mathrm{C}_{\mathrm{V}}\) for gas 1 and \(\mathrm{nC}_P\) and \(\mathrm{nC}_{\mathrm{V}}\) for gas 2 . Thus for the mixture, heat capacities will be
\(
\mathrm{C}_{\mathrm{V}}^{\prime}=\frac{\mathrm{C}_{\mathrm{V}}+2 \mathrm{nC}_{\mathrm{V}}}{3}=\frac{1+2 \mathrm{n}}{3} \mathrm{C}_{\mathrm{V}}
\)
Also, \(C_P^{\prime}=\frac{C_P+2 n C_p}{3}=\frac{1+2 n}{3} C_P\)
Thus, for the mixture,
\(
\gamma^{\prime}=\frac{\mathrm{C}_{\mathrm{P}}^{\prime}}{\mathrm{C}_{\mathrm{V}}^{\prime}}=\frac{\mathrm{C}_{\mathrm{P}}}{\mathrm{C}_{\mathrm{V}}}=\gamma
\) -
Question 77 of 102
77. Question
A mixture contains 1 mole of helium \(\left(C_p=25 R\right.\), \(\left.C_V=1.5 \mathrm{R}\right)\) and 1 mole of hydrogen \(\left(C_p=3.5 \mathrm{R}\right.\), \(C_V=2.5 \mathrm{R}\) ). Calculate the values of \(C_p, C_V\) and \(\gamma\) for the mixture.
CorrectIncorrectHint
\(
\begin{aligned}
& C_p=\frac{n_1 C_{p 1}+n_2 C_{p 2}}{n_1+n_2} \\
& =\frac{2.5 R+3.5 R}{1+1}=3 R \\
& C_V=\frac{n_1 C_{V 1}+n_2 C_{V 2}}{n_1+n_2} \\
& =\frac{1.5 R+2.5 R}{2}=2 R \\
& \gamma=\frac{C_p}{C_V}=\frac{3}{2}=1.5 .
\end{aligned}
\) -
Question 78 of 102
78. Question
Half mole of an ideal gas \((\gamma=5 / 3)\) is taken through the cycle \(a b c d a\) as shown in the figure below. Take \(R=\frac{25}{3} \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\). (a) Find the temperature of the gas in the states \(a, b, c\) and \(d\). (b) Find the amount of heat supplied in the processes \(a b\) and \(b c\). (c) Find the amount of heat liberated in the processes \(c d\) and \(d a\).
 CorrectIncorrect
CorrectIncorrectHint
\(
\begin{aligned}
n & =\frac{1}{2} \mathrm{~mol} . \\
R & =\frac{25}{3} \mathrm{~J} / \mathrm{mol} . \cdot k \\
\gamma & =\frac{5}{3}
\end{aligned}
\)
(a) Temperature at \(a=T a\),
\(P a V a=n R T a\)
implies \(T a=\frac{P a V a}{n R}=120 K\)
Similarly, temperature at \(b=240 K\), at c it is \(480 K\) and at \(d\) it is \(240 K\).
(b) For \(a b\) process
\(
d Q=n c_p d T
\)
[Since \(a b\) is isometric]
\(
\begin{aligned}
& =\frac{1}{2} \times \frac{R \gamma}{\gamma-1}(T b-T a) \\
& =\frac{1}{2} \times \frac{\frac{25 \times 5}{3 \times 3}}{\frac{5}{3}-1} \times(240-120) \\
& =\frac{1}{2} \times \frac{125}{9} \times \frac{3}{2} \times(120) \\
& =1250 J \\
& \text { For } b c, d Q=d U+d W \\
& {[d W=0, \text { Isochoric process] }} \\
& =n C_v(T c-T b) \\
& =\frac{1}{2} \times \frac{\left(\frac{25}{3}\right)}{\left[\left(\frac{5}{3}\right)-1\right]} \times(240) \\
& =\frac{1}{2} \times \frac{25}{3} \times \frac{3}{2} \times 240=1500 J .
\end{aligned}
\)
(c) Heat liberated in \(c d=-n C_p d T\)
\(
\mathrm{dQ}=-\frac{1}{2} \times \frac{\gamma \mathrm{R}}{\gamma-1} \times\left(\mathrm{T}_d-\mathrm{T}_{\mathrm{c}}\right)
\)
\(
\begin{aligned}
& =-\frac{1}{2} \times \frac{125}{9} \times \frac{3}{2} \times(240-480) \\
& =-\frac{1}{2} \times \frac{125}{6} \times 240=2500 J
\end{aligned}
\)
Heat liberated in \(d a\)
\(
\begin{aligned}
& =-n C v d T \\
& =-\frac{1}{2} \times \frac{R}{\gamma-1}(T a-T d) \\
& =-\frac{1}{2} \times \frac{25}{2} \times(120-240) \\
& =\frac{25}{4} \times 120=750 J
\end{aligned}
\) -
Question 79 of 102
79. Question
An ideal gas \((\gamma=1.67)\) is taken through the process \(a b c\) shown in figure below. The temperature at the point \(a\) is \(300 \mathrm{~K}\). Calculate (a) the temperatures at \(b\) and \(c\), (b) the work done in the process, (c) the amount of heat supplied in the path \(a b\) and in the path \(b c\) and (d) the change in the internal energy of the gas in the process.
 CorrectIncorrect
CorrectIncorrectHint
(a) For line ab, volume is constant. So, from the ideal gas equation,
\(
\begin{aligned}
& \frac{P_1}{T_1}=\frac{P_2}{T_2} \\
& \Rightarrow \frac{100}{300}=\frac{200}{T_2}
\end{aligned}
\)
\(
\mathrm{T}_2=\left(\frac{200 \times 300}{100}\right)=600 \mathrm{~K}
\)
For line \(b c\), pressure is constant.
\(
\begin{aligned}
& \text { So, } \frac{\mathrm{V}_1}{\mathrm{~T}_1}=\frac{\mathrm{V}_2}{\mathrm{~T}_2} \\
& \Rightarrow \mathrm{T}_2=\left(\frac{600 \times 150}{100}\right)=900 \mathrm{~K}
\end{aligned}
\)
(b) As process \(a b\) is isochoric, \(W_{a b}=0\).
During the process bc, \(\mathrm{P}=200 \mathrm{kPa}\)
The volume is changing from 100 to \(150 \mathrm{~cm}^3\).
\(
\begin{aligned}
\text { Therefore, work done } & =50 \times 10^{-6} \times 200 \times 10^3 \mathrm{~J}=10 \mathrm{~J} \\
\end{aligned}
\)
(c) For ab (isochoric process), work done \(=0\).
From the first law,
\(
\begin{aligned}
& \mathrm{dQ}=\mathrm{dU}=\mathrm{nC}_{\mathrm{v}} \mathrm{dT} \\
& \Rightarrow \text { Heat supplied }=\mathrm{nC}_{\mathrm{v}} \mathrm{dT}
\end{aligned}
\)
Now,
\(
\begin{aligned}
& \mathrm{Q}_{\mathrm{ab}}=\left(\frac{\mathrm{PV}}{\mathrm{RT}}\right) \times\left(\frac{\mathrm{R}}{\gamma-1}\right) \times \mathrm{dT} \\
& =\frac{200 \times 10^3 \times 100 \times 10^{-6} \times 300}{600 \times 0.67} \\
& =14.925(\therefore \gamma=1.67)
\end{aligned}
\)
For bc (isobaric process) :
Heat supplied in \(b c=nC_p d T \quad\left(C_p=\frac{\gamma R}{\gamma-1}\right)\)
\(
\begin{aligned}
& =\frac{\mathrm{PV}}{\mathrm{RT}} \times \frac{\gamma \mathrm{R}}{\gamma-1} \times \mathrm{dT} \\
& =\frac{200 \times 10^3 \times 150 \times 10^{-6}}{600 \times 0.67} \times 300 \\
& =10 \times \frac{1.67}{0.67}=\frac{16.7}{0.67}=24.925
\end{aligned}
\)
(d) \(d Q=d U+d W\)
Now,
\(
\begin{aligned}
\mathrm{dU} & =\mathrm{dQ}-\mathrm{dW} \\
& =\text { Heat supplied }-\text { Work done } \\
& =(24.925+14.925)-10 \\
& =39.850-10=29.850 \mathrm{~J}
\end{aligned}
\) -
Question 80 of 102
80. Question
In Joly’s differential steam calorimeter, \(3 \mathrm{~g}\) of an ideal gas is contained in a rigid closed sphere at \(20^{\circ} \mathrm{C}\). The sphere is heated by steam at \(100^{\circ} \mathrm{C}\) and it is found that an extra \(0.095 \mathrm{~g}\) of steam has condensed into water as the temperature of the gas becomes constant. Calculate the specific heat capacity of the gas in \(\mathrm{J} \mathrm{g}^{-1} \mathrm{~K}^{-1}\). The latent heat of vaporization of water \(=540 \mathrm{cal} \mathrm{g}^{-1}\).
CorrectIncorrectHint
For Joly’s differential steam calorimeter,
\(
C_v=\frac{m_2 \mathrm{~L}}{m_1}\left(\theta_2-\theta_1\right)
\)
where
\(
\begin{aligned}
& m_2=\text { mass of steam condensed } \\
& m_2=0.095 \mathrm{~g}
\end{aligned}
\)
Latent heat of vapourization, \(\mathrm{L}=540 \mathrm{cal} / \mathrm{g}=540 \times 4.2 \mathrm{~J} / \mathrm{g}\)
\(\mathrm{m}_1=\) mass of \(\mathrm{gas}\) present
\(
\mathrm{m}_1=3 \mathrm{~g}
\)
Initial temperature, \(\theta_1=20^{\circ} \mathrm{C}\)
Final temperature, \(\theta_2=100^{\circ} \mathrm{C}\)
\(
\begin{aligned}
& \Rightarrow C_v=\frac{0.095 \times 540 \times 4.2}{3 \times(100-20)} \\
& =0.89=0.9 \mathrm{g}^{-1} \mathrm{~K}^{-1}
\end{aligned}
\) -
Question 81 of 102
81. Question
The volume of an ideal gas \((\gamma=1.5)\) is changed adiabatically from \(4.00\) litres to \(3.00\) litres. Find the ratio of (a) the final pressure to the initial pressure and (b) the final temperature to the initial temperature.
CorrectIncorrectHint
\(
\gamma=1.5
\)
Since it is an adiabatic process, So \(\mathrm{PV}^{\gamma}=\) const.
(a) \(P_1 V_1^\gamma=P_2 V_2^\gamma \quad\) Given \(V_1=4 L, V_2=3 L, \quad \frac{P_2}{P_1}=\) ?
\(
\Rightarrow \frac{P_2}{P_1}=\left(\frac{V_1}{V_2}\right)^\gamma=\left(\frac{4}{3}\right)^{1.5}=1.5396 \approx 1.54
\)
(b) TV \(^{\gamma-1}=\) Const.
\(
T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1} \Rightarrow \frac{T_2}{T_1}=\left(\frac{V_1}{V_2}\right)^{\gamma-1}=\left(\frac{4}{3}\right)^{0.5}=1.154
\) -
Question 82 of 102
82. Question
An ideal gas at pressure \(2.5 \times 10^5 \mathrm{~Pa}\) and temperature \(300 \mathrm{~K}\) occupies \(100 \mathrm{cc}\). It is adiabatically compressed to half its original volume. Calculate (a) the final pressure, (b) the final temperature, and (c) the work done by the gas in the process. Take \(\gamma=1.5\).
CorrectIncorrectHint
Initial pressure of the gas, \(\mathrm{P}_1=2.5 \times 10^5 \mathrm{~Pa}\)
Initial temperature, \(T_1=300 \mathrm{~K}\)
Initial volume, \(\mathrm{V}_1=100 \mathrm{cc}\)
(a) For an adiabatic process,
\(
\begin{aligned}
& P_1 V_1{ }^\gamma=P_2 V_2{ }^\gamma \\
& \Rightarrow 2.5 \times 10^5 \times V^{1.5}=\left(\frac{\mathrm{V}}{2}\right)^{1.5} \times P_2 \\
& \Rightarrow P_2=7.07 \times 10^5 \\
& =7.1 \times 10^5 \mathrm{~Pa}
\end{aligned}
\)
(b) Also, for an adiabatic process,
\(
\begin{aligned}
& T_1 V_1{ }^{\gamma-1}=T_2 V_2{ }^{\gamma-1} \\
& \Rightarrow 300 \times(100)^{1.5-1}=T_2 \times\left(\frac{100}{2}\right)^{1.5-1} \\
& =T_2 \times(50)^{1.5-1} \\
& \Rightarrow 300 \times 10=T_2 \times 7.07 \\
& \Rightarrow T_2=424.32 \mathrm{~K}=424 \mathrm{~K}
\end{aligned}
\)
(c) Work done by the gas in the process,
\(
\begin{aligned}
& W=\frac{\mathrm{nR}}{(\gamma-1)}\left[\mathrm{T}_1-\mathrm{T}_2\right] \\
& =\frac{\mathrm{P}_1 \mathrm{~V}_1}{\mathrm{~T}(\gamma-1)}\left[\mathrm{T}_1-\mathrm{T}_2\right] \\
& =\frac{2.5 \times 10}{300 \times 0.5} \times(-124) \\
& =-20.67 \approx-21 J
\end{aligned}
\) -
Question 83 of 102
83. Question
Air \((\gamma=1.4)\) is pumped at 2 atm pressure in a motor tyre at \(20^{\circ} \mathrm{C}\). If the tyre suddenly bursts, what would be the temperature of the air coming out of the tyre. Neglect any mixing with the atmospheric air.
CorrectIncorrectHint
Given:
For air, \(\gamma=1.4\)
Initial temperature of air, \(\mathrm{T}_1=20^{\circ} \mathrm{C}=293 \mathrm{~K}\)
Initial pressure, \(\mathrm{P}_1=2 \mathrm{~atm}\)
Final pressure, \(P_2=1 \mathrm{~atm}\)
The bursting of the tyre is an adiabatic process. For an adiabatic process,
\(
\mathrm{P}_1{ }^{1-\gamma} \times \mathrm{T}_1{ }^{1-\gamma}=\mathrm{P}_2{ }^{1-\gamma} \times \mathrm{T}_2{ }^\gamma
\)
\((2)^{1-1.4} \times(293)^{1.4}=(1)^{1-1.4} \times T_2^{1.4}\)
\(
\begin{aligned}
& \Rightarrow(2)^{-0.4} \times(293)^{1.4}=\mathrm{T}_2^{1.4} \\
& \Rightarrow 2153.78=\mathrm{T}_2^{1.4} \\
& \Rightarrow \mathrm{T}_2=(2153.78)^{1 / 1.4} \\
& =240.3 \mathrm{~K}
\end{aligned}
\) -
Question 84 of 102
84. Question
A gas is enclosed in a cylindrical can fitted with a piston. The walls of the can and the piston are adiabatic. The initial pressure, volume, and temperature of the gas are \(100 \mathrm{kPa}, 400 \mathrm{~cm}^3\) and \(300 \mathrm{~K}\) respectively. The ratio of the specific heat capacities of the gas is \(C_p / C_V=1 \cdot 5\). Find the pressure and the temperature of the gas if it is (a) suddenly compressed (b) slowly compressed to \(100 \mathrm{~cm}^3\)
CorrectIncorrectHint
Initial pressure of the gas, \(\mathrm{P}_1=100 \mathrm{kPa}\)
Initial volume of the gas, \(V_1=400 \mathrm{~cm}^3=400 \times 10^{-6} \mathrm{~m}^3\)
Initial temperature of the gas, \(T_1=300 \mathrm{~K}\)
\(
\gamma=\frac{C_p}{C_v}=1.5
\)
(a) The gas is suddenly compressed to volume, \(V_2=100 \mathrm{~cm}^3\).
So, this is an adiabatic process.
For an adiabatic process,
\(
\begin{aligned}
& P_1 V_1{ }^\gamma=P_2 V_2{ }^\gamma \\
& \Rightarrow 10^5 \times(400)^{1.5}=P_2(100)^{1.5} \\
& \Rightarrow P_2=10^5(4)^{1.5}=800 \mathrm{kPa}
\end{aligned}
\)
Also,
\(
\begin{aligned}
& T_1 V^{\gamma-1}=T_2 V_2^{\gamma-1} \\
& \Rightarrow 300 \times(400)^{1.5-1}=T_2(100)^{1.5-1} \\
& \Rightarrow 300 \times(400)^{0.5}=T_2(100)^{0.5} \\
& \Rightarrow T_2=600 \mathrm{~K}
\end{aligned}
\)
(b) If the container is slowly compressed, the heat transfer is zero, even thought the walls are adiabatic. Thus, the values remain same. Thus,
\(
\begin{aligned}
& \mathrm{P}_2=800 \mathrm{kPa} \\
& \mathrm{T}_2=600 \mathrm{~K}
\end{aligned}
\) -
Question 85 of 102
85. Question
The initial pressure and volume of a given mass of a gas \(\left(C_p / C_V=\gamma\right)\) are \(p_0\) and \(V_0\). The gas can exchange heat with the surrounding. (a) It is slowly compressed to a volume \(V_0 / 2\) and then suddenly compressed to \(V_0 / 4\). Find the final pressure. (b) If the gas is suddenly compressed from the volume \(V_0\) to \(V_0 / 2\) and then slowly compressed to \(V_0 / 4\), what will be the final pressure?
CorrectIncorrectHint
Given:
For the gas, \(\frac{C_p}{C_v}=\gamma\)
Initial pressure of the gas \(=P_0\)
Initial volume of the gas \(=\mathrm{V}_0\)
(a)
(i) As the gas is slowly compressed, its temperature will remain constant.
For isothermal compression,
\(
P_1 V_1=P_2 V_2
\)
So, \(\mathrm{P}_0 \mathrm{~V}_0=\mathrm{P}_2 \frac{\mathrm{V}_0}{2} \Rightarrow \mathrm{P}_2=2 \mathrm{P}_0\)
(ii) Sudden compression means that the gas could not get sufficient time to exchange heat with its surroundings. So, it is an adiabatiac compression.
So, for adiabatic compression,
\(
\begin{aligned}
& \mathrm{P}_1 \mathrm{~V}_1{ }^\gamma=\mathrm{P}_2 \mathrm{~V}_2{ }^\gamma \text { Or } \\
& 2 \mathrm{P}_0\left(\frac{\mathrm{V}_0}{2}\right)^\gamma=\mathrm{P}_2\left(\frac{\mathrm{V}_0}{4}\right)^\gamma \\
& \Rightarrow \mathrm{P}_2=\frac{\mathrm{V}_0^\gamma}{2^\gamma} \times 2 \mathrm{P}_0 \times \frac{4^\gamma}{\mathrm{V}_0^\gamma} \\
& =2^\gamma \times 2 \mathrm{P}_0=\mathrm{P}_0 2^{\gamma+1}
\end{aligned}
\)
(i) Adiabatic compression:
\(
\begin{aligned}
& P_1 V_1 \gamma=P_2 V_2^\gamma \\
& P_0 V_0^\gamma=P^{\prime}\left(\frac{V_0}{2}\right)^\gamma \\
& \Rightarrow P^{\prime}=P_0 2^\gamma
\end{aligned}
\)
(ii) Isothermal compression:
\(
\begin{aligned}
& \mathrm{P}_1 \mathrm{~V}_1=\mathrm{P}_2 \mathrm{~V}_2 \\
& 2^\gamma \mathrm{P}_0 \times \frac{\mathrm{V}_0}{2}=\mathrm{P}^{\prime \prime}\left(\frac{V_0}{2}\right) \\
& \mathrm{P}^{\prime \prime}=\mathrm{P}_0 2^{\mathrm{\gamma}} \times 2 \\
& \Rightarrow \mathrm{P}^{\prime \prime}=\mathrm{P}_0 2 ^{\gamma+1}
\end{aligned}
\) -
Question 86 of 102
86. Question
Consider a given sample of an ideal gas \(\left(C_p / C_V=\gamma\right)\) having initial pressure \(p_0\) and volume \(V_0\). (a) The gas is isothermally taken to a pressure \(p_0 / 2\) and from there adiabatically to a pressure \(p_0 / 4\). Find the final volume. (b) The gas is brought back to its initial state. It is adiabatically taken to a pressure \(p_0 / 2\) and from there isothermally to a pressure \(p_0 / 4\). Find the final volume.
CorrectIncorrectHint
(a) Given,
Initial pressure of the gas \(=p_0\)
Initial volume of the gas \(=\mathrm{V}_0\)
For an isothermal process,
\(\mathrm{PV}=\) constant
So, \(P_1 V_1=P_2 V_2\)
\(
P_2=\frac{P_0 V_0}{\frac{P_0}{2}}=2 \mathrm{~V}_0
\)
For an adiabatic process, \(P_3=\frac{P_0}{4}, V_3=\) ?
\(
\begin{aligned}
& P_2 V_2^\gamma=P_3 V_3^\gamma \\
& \Rightarrow\left(\frac{V_3}{V_2}\right)^\gamma=\left(\frac{P_2}{P_3}\right) \\
& \Rightarrow\left(\frac{V_3}{V_2}\right)^\gamma=\left(\frac{\frac{P_0}{2}}{\frac{P_0}{4}}\right)=2 \\
& \Rightarrow \frac{V_3}{V_2}=2^{\frac{1}{\gamma}} \\
& \therefore V_3=V_2 2^{\frac{1}{\gamma}}=2 V_0 2^{\frac{1}{\gamma}} \\
& =2^{\frac{\gamma+1}{\gamma}} V_0
\end{aligned}
\)
\(
\begin{aligned}
& \text { (b) } P_1 V_1{ }^{\gamma}=P_2 V_2{ }^{\gamma}\\
& \operatorname{Or}\left(\frac{V_2}{V_1}\right)=\left(\frac{P_1}{P_2}\right)^{\frac{1}{\gamma}} \\
& \Rightarrow V_2=V_0 2^{\frac{1}{\gamma}}
\end{aligned}
\)
Again, for an isothermal process,
\(
\begin{aligned}
& P_2 V_2=P_3 V_3 \\
& \therefore V_3=\frac{P_2 V_2}{P_3}=2 \times 2^{\frac{1}{\gamma}} V_0 \\
& =2^{\frac{\gamma+1}{\gamma}} V_0
\end{aligned}
\) -
Question 87 of 102
87. Question
A sample of an ideal gas \((\gamma=1 \cdot 5)\) is compressed adiabatically from a volume of \(150 \mathrm{~cm}^3\) to \(50 \mathrm{~cm}^3\). The initial pressure and the initial temperature are \(150 \mathrm{kPa}\) and \(300 \mathrm{~K}\). Find (a) the number of moles of the gas in the sample, (b) the molar heat capacity at constant volume.
CorrectIncorrectHint
The ideal gas equation is
\(
P V=n R T
\)
Given, \(P_1=150 \mathrm{kPa}=150 \times 10^3 \mathrm{~Pa}\)
\(
\begin{aligned}
& V_1=150 \mathrm{~cm}^3=150 \times 10^{-6} \mathrm{~m}^3 \\
& T_1=300 \mathrm{~K}
\end{aligned}
\)
(a)
\(
\begin{aligned}
& \mathrm{n}=\frac{\mathrm{PV}}{\mathrm{RT}}=9.036 \times 10^{-3} \\
& \mathrm{n}=0.009
\end{aligned}
\)
(b)
\(
\frac{C_p}{C_v}=\gamma, C_p-C_v=R
\)
So, \(C_{\mathrm{v}}=\frac{\mathrm{R}}{\gamma-1}=2 \mathrm{R}=\frac{8.3}{0.5}=16.6 \mathrm{Jmol}-\mathrm{K}\) -
Question 88 of 102
88. Question
A sample of an ideal gas \((\gamma=1 \cdot 5)\) is compressed adiabatically from a volume of \(150 \mathrm{~cm}^3\) to \(50 \mathrm{~cm}^3\). The initial pressure and the initial temperature are \(150 \mathrm{kPa}\) and \(300 \mathrm{~K}\). Find (a) the final pressure and temperature, (b) the work done by the gas in the process, and (c) the change in internal energy of the gas.
CorrectIncorrectHint
(a) Given,
\(
\begin{aligned}
& P_1=150 \mathrm{kPa}=150 \times 10^3 \mathrm{~Pa} \\
& P_2=? V_1=150 \mathrm{~cm}^3 \\
& =150 \times 10^{-6} \mathrm{~m}^3 \\
& \gamma=1.5 \\
& V_2=50 \mathrm{~cm}^3=50 \times 10^{-6} \mathrm{~m}^3, \\
& T_1=300 \mathrm{~K} \\
& T_2=?
\end{aligned}
\)
Since the process is adiabatic, using the equation of an adiabatic process, we get
\(
\begin{aligned}
& P_1 V_1^\gamma=P_2 V_2^\gamma \\
& \Rightarrow 150 \times 10^3 \times\left(150 \times 10^{-6}\right)^\gamma=P_2 \times\left(50 \times 10^{-6}\right)^\gamma \\
& \Rightarrow P_2=150 \times 10^3 \times \frac{\left(150 \times 10^{-6}\right)^{1.5}}{\left(50 \times 10^{-6}\right)^{1.5}} \\
& P_2=150000 \times(3)^{1.5} \\
& P_2=779.422 \times 10^3 \mathrm{~Pa} \\
& P_2=780 \mathrm{kPa}
\end{aligned}
\)
Again,
\(
\begin{aligned}
& P_1{ }^{1-\gamma} T_1{ }^\gamma=P_2{ }^{1-\gamma} T_2{ }^\gamma \\
& \Rightarrow\left(150 \times 10^3\right)^{1-1.5} \times(330)^{1.5}=\left(780 \times 10^3\right)^{1-1.5} \times T_2^{1.5} \\
& \Rightarrow T_2^{1.5}=\left(150 \times 10^3\right)^{1-1.5} \times(300)^{1.5} \times 300^{1.5} \\
& T_2{ }^{1.5}=11849.050 \\
& \Rightarrow T_2=(11849.050)^{1 / 1.5} \\
& T_2=519.74=520 \mathrm{~K}
\end{aligned}
\)
(b) \(\mathrm{dQ}=\mathrm{dW}+\mathrm{dU}\)
Or \(\mathrm{dW}=-\mathrm{dU}\) [ Since \(\mathrm{dQ}=0\) in an adiabatic process]
\(
\begin{aligned}
& d W=-C_v d T \\
& d W=-0.009 \times 16.6 \times(520-300) \\
& d W=-0.009 \times 16.6 \times 220 \\
& d W=-32.87 \mathrm{~J} \approx-33 \mathrm{~J}
\end{aligned}
\)
(c)
\(
\begin{aligned}
& d U=n C_v d T \\
& d U=0.009 \times 16.6 \times 220 \approx 33 J
\end{aligned}
\) -
Question 89 of 102
89. Question
Three samples \(A, B\) and \(C\) of the same gas \((\gamma=1 \cdot 5)\) have equal volumes and temperatures. The volume of each sample is doubled, the process being isothermal for \(A\), adiabatic for \(B\) and isobaric for \(C\). If the final pressures are equal for the three samples, find the ratio of the initial pressures.
CorrectIncorrectHint
There are three gases \(\mathrm{A}, \mathrm{B}\) and \(\mathrm{C}\).
It is given that initially,
\(V_A=V_B=V_C\) and \(T_A=T_B=T_C\).
For \(\mathrm{A}\), the process is isothermal and for an isothermal process, \(\mathrm{PV}=\) constant.
\(
\begin{aligned}
& \mathrm{P}_{\mathrm{A}} \mathrm{V}_{\mathrm{A}}=\mathrm{P}_{\mathrm{A}}^{\prime} 2 \mathrm{~V}_{\mathrm{A}} \\
& \mathrm{P}_{\mathrm{A}}^{\prime}=\mathrm{P}_{\mathrm{A}} \times \frac{1}{2}
\end{aligned}
\)
For B, the process is adiabatic. So,
\(
\begin{aligned}
& P_B V_B{ }^\gamma=P_B^{\prime}\left(2 V_B\right)^\gamma \\
& \Rightarrow P_B^{\prime}=\frac{P_B}{2^{1.5}}
\end{aligned}
\)
For \(C\), the process is isobaric, which implies that the pressure will remain constant.
So, using the ideal gas equation
\(
\begin{aligned}
& P=\frac{n R T}{V} \text { we get } \\
& \frac{V_c}{T_c}=\frac{V_c^{\prime}}{T_c^{\prime}} \Rightarrow \frac{V_c}{T_c}=\frac{2 V_c}{T_c^{\prime}} \\
& \Rightarrow T_C^{\prime}=2 T_C
\end{aligned}
\)
As the final pressures are equal,
\(
\begin{aligned}
& \frac{P_A}{2}=\frac{P_B}{2^{1.5}}=P_C \\
& \Rightarrow P_A: P_B: P_C=2: 2^{1.5}: 1=2: 2 \sqrt{2}: 1
\end{aligned}
\) -
Question 90 of 102
90. Question
Two samples \(A\) and \(B\) of the same gas have equal volumes and pressures. The gas in sample \(A\) is expanded isothermally to double its volume and the gas in \(B\) is expanded adiabatically to double its volume. If the work done by the gas is the same for the two cases, then \(\gamma\) satisfies the equation \(1-2^{1-\gamma}=(\gamma-1) \ln 2\). Is this true?
CorrectIncorrectHint
Let,
Initial pressure of the gas \(=P_1\)
Initial volume of the gas \(=\mathrm{V}_1\)
Final pressure of the gas \(=P_2\)
Final volume of the gas \(=V_2\)
Given, \(V_2=2 V_1\), for each case.
In an isothermal expansion process,
work done \(=\mathrm{nRT}_1 \ln \frac{\mathrm{V}_2}{\mathrm{~V}_1}\)
Adiabatic work done,
\(
\mathrm{W}=\frac{\mathrm{P}_1 \mathrm{~V}_1-\mathrm{P}_2 \mathrm{~V}_2}{\gamma-1}
\)
It is given that same work is done in both cases.
So,
\(
n R T_1 \ln \left(\frac{\mathrm{V}_2}{\mathrm{~V}_1}\right)=\frac{\mathrm{P}_1 \mathrm{~V}_1-\mathrm{P}_2 \mathrm{~V}_2}{\gamma-1} . . \text { (1) }
\)
In an adiabatic process,
\(
\mathrm{P}_2=\mathrm{P}_1\left(\frac{\mathrm{V}_1}{\mathrm{~V}_2}\right)^\gamma=\mathrm{P}_1\left(\frac{1}{2}\right)^\gamma
\)
From eq (1),
\(
\mathrm{nRT}_1 \ln 2=\frac{\mathrm{P}_1 \mathrm{~V}_1\left(1-\frac{1}{2^\gamma} \times 2\right)}{\gamma-1}
\)
and \(\mathrm{nR} T_1=\mathrm{P}_1 \mathrm{~V}_1\)
So, \(\ln 2=\frac{1-\frac{1}{2^\gamma} \cdot 2}{\gamma-1}\)
\(\operatorname{Or}(\gamma-1) \ln 2=1-2^{1-\gamma}\) -
Question 91 of 102
91. Question
1 litre of an ideal gas \((\gamma=1.5)\) at \(300 \mathrm{~K}\) is suddenly compressed to half its original volume. (a) Find the ratio of the final pressure to the initial pressure. (b) If the original pressure is \(100 \mathrm{kPa}\), find the work done by the gas in the process. (c) What is the change in internal energy? (d) What is the final temperature?
CorrectIncorrectHint
Given:
\(
\begin{aligned}
& \gamma=1.5 \\
& T=300 \mathrm{~K}
\end{aligned}
\)
Initial volume of the gas, \(V_1=1 \mathrm{~L}\)
Final volume, \(V_2=\frac{1}{2} L\)
(a) The process is adiabatic because volume is suddenly changed; so, no heat exchange is allowed.
\(
P_1 V_1{ }^{\gamma}=P_2 V_2{ }^{\gamma}
\)
Or \(P_2=P_1\left(\frac{V_1}{V_2}\right)^\gamma=P_1(2)^\gamma\)
\(
\frac{P_2}{P_1}=2^{1.5}=2 \sqrt{2}
\)
(b) \(P_1=100 \mathrm{kPa}=10^5 \mathrm{~Pa}\)
and \(P_2=2 \sqrt{2} \times 10^5 \mathrm{~Pa}\)
Work done by an adiabatic process,
\(
\begin{aligned}
& W=\frac{P_1 \mathrm{~V}_1-\mathrm{P}_2 \mathrm{~V}_2}{\gamma-1} \\
& \mathrm{~W}=\frac{10^5 \times 10^{-3}-2 \sqrt{2} \times 10^5 \times \frac{1}{2} \times 10^{-3}}{1.5-1} \\
& \mathrm{~W}=-82 \mathrm{~J}
\end{aligned}
\)
(c) Internal energy,
\(d Q=0\), as it is an adiabatic process.
\(
\Rightarrow \mathrm{d} U=-\mathrm{d} W=-(-82 \mathrm{~J})=82 \mathrm{~J}
\) -
Question 92 of 102
92. Question
1 litre of an ideal gas \((\gamma=1 \cdot 5)\) at \(300 \mathrm{~K}\) is suddenly compressed to half its original volume. (a) What is the final temperature? (b) The gas is now cooled to \(300 \mathrm{~K}\) keeping its pressure constant. Calculate the work done during the process. (c) The gas is now expanded isothermally to achieve its original volume of 1 litre. Calculate the work done by the gas. (d) Calculate the total work done in the cycle.
CorrectIncorrectHint
(a)
Also, for an adiabatic process,
\(
\begin{aligned}
& T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1} \\
& T_2=T_1\left(\frac{V_1}{V_2}\right)^{\gamma-1} \\
& =300 \times(2)^{0.5} \\
& =300 \times \sqrt{2} \times=300 \times 1.4142 \\
& T_2=424 \mathrm{~K}
\end{aligned}
\)
(b) The pressure is kept constant.
The process is isobaric; so, work done \(=P \Delta V=n R d T\).
Here, \(n=\frac{P V}{R T}=\frac{10^5 \times 10^{-3}}{R \times 300}=\frac{1}{3 R}\)
So, work done \(=\frac{1}{3 R} \times R \times(300-424)=-41.4 \mathrm{~J}\)
As pressure is constant,
\(
\begin{aligned}
& \frac{\mathrm{V}_1}{\mathrm{~T}_1}=\frac{\mathrm{V}_2}{\mathrm{~T}_2} \ldots(1) \\
& \mathrm{V}_1=\mathrm{V}_2 \frac{\mathrm{T}_1}{\mathrm{~T}_2}
\end{aligned}
\)
(c)Work done in an isothermal process,
\(
\begin{aligned}
& W=n R T \ln \frac{V_2}{V_1} \\
& =\frac{1}{3 R} \times R \times T \times \ln (2) \\
& =100 \times \ln 2=100 \times 1.039 \\
& =103 \mathrm{~J}
\end{aligned}
\)
(d) Net work done (using first law of thermodynamics)
\(
\begin{aligned}
& =-82-41.4+103 \\
& =-20.4 \mathrm{~J}
\end{aligned}
\) -
Question 93 of 102
93. Question
Figure below shows a cylindrical tube with adiabatic walls and fitted with an adiabatic separator. The separator can be slid into the tube by an external mechanism. An ideal gas \((\gamma=1 \cdot 5)\) is injected in the two sides at equal pressures and temperatures. The separator remains in equilibrium at the middle. It is now slid to a position where it divides the tube in the ratio \(1: 3\). Find the ratio of the temperatures in the two parts of the vessel.
 CorrectIncorrect
CorrectIncorrectHint
\(
\gamma=1.5
\)
For an adiabatic process, TV \(^{\gamma-1}=\) constant.
So, \(T_1 V_1{ }^{\gamma-1}=T_2 V_2{ }^{\gamma-1}\)
As it is an adiabatic process and all the other conditions are same, the above equation can be applied. In the new position, the slid is dividing the tube in the ratio \(3: 1\).
So, if the total volume is \(V\), then one side will occupy a volume of \(\frac{3}{4} \mathrm{~V}\) and the other side will occupy \(\frac{\mathrm{V}}{4}\).
So, \(\mathrm{T}_1 \times\left(\frac{3 \mathrm{v}}{4}\right)^{\gamma-1}=\mathrm{T}_2 \times\left(\frac{\mathrm{v}}{4}\right)^{\gamma-1}\)
\(
\begin{aligned}
& \Rightarrow \mathrm{T}_1 \times\left(\frac{3 \mathrm{v}}{4}\right)^{1.5-1}=\mathrm{T}_2 \times\left(\frac{\mathrm{v}}{4}\right)^{1.5-1} \\
& \frac{\mathrm{T}_1}{\mathrm{~T}_2}=\frac{\sqrt{3}}{1}
\end{aligned}
\)
-
Question 94 of 102
94. Question
Figure below shows two rigid vessels \(A\) and \(B\), each of volume \(200 \mathrm{~cm}^3\) containing an ideal gas \(\left(C_V=12.5\right.\) \(\mathrm{J} \mathrm{K}^{-1} \mathrm{~mol}^{-1}\) ). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is \(75 \mathrm{~cm}\) of mercury and the temperature is \(300 \mathrm{~K}\) (a) Find the number of moles of the gas in each vessel. (b) \(5.0 \mathrm{~J}\) of heat is supplied to the gas in the vessel \(A\) and \(10 \mathrm{~J}\) to the gas in the vessel \(B\). Assuming no appreciable transfer of heat from \(A\) to \(B\) calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant \(R=8.3 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\).
 CorrectIncorrect
CorrectIncorrectHint
Given:
Volume of gas in each vessel, \(V=200 \mathrm{~cm}^3\)
Specific heat at constant volume of the gas, \(C_{\mathrm{V}}=12.5 \mathrm{~J} / \mathrm{mol}-\mathrm{K}\)
Initial temperature of the gas, \(\mathrm{T}=300 \mathrm{~K}\)
Initial pressure of the gas, \(P=75 \mathrm{~cm}\) of \(\mathrm{Hg}\)
(a) Using the ideal gas equation, number of moles of gases in each vessel,
\(75 \mathrm{~cm}\) of \(\mathrm{Hg}=99991.5 \mathrm{~N} / \mathrm{m}^2\)
\(n=\frac{P V}{R T}\)
\(=\frac{99991.5 \times 200 \times 10^{-6}}{8.3 \times 300}\)
\(=8031.4 \times x \times 10^{-6}\)
\(=0.008\)
(b) Heat is supplied to the gas, but \(\mathrm{dV}\) is zero as the container has rigid walls.
So, \(\mathrm{dW}=\mathrm{P} \Delta \mathrm{V}=0\)
From first law of thermodynamics,
\(
\begin{aligned}
& \mathrm{dQ}=\mathrm{dU} \\
& \Rightarrow 5=\mathrm{nC}_{\mathrm{v}} \mathrm{dT} \\
& \Rightarrow 5=0.008 \times 12.5 \times \mathrm{dT} \\
& \Rightarrow \mathrm{dT}=50 \text { for } \mathrm{A}
\end{aligned}
\)
\(\frac{P}{T}=\frac{P_A}{T_A}\) because volume is kept constant.
\(
Q=nC_v d T
\)
\(
\begin{aligned}
& \mathrm{T}=\frac{\mathrm{Q}}{\mathrm{nC}_{\mathrm{V}}} \\
& \frac{75}{300}=\frac{\mathrm{P}_{\mathrm{A}} \times 0.008 \times 12.5}{5} \\
& \mathrm{P}_{\mathrm{A}}=\frac{75 \times 5}{300 \times 0.008 \times 12.5} \\
& =12.5 \mathrm{~cm} \text { of } \mathrm{Hg}
\end{aligned}
\)
Again,\(\frac{\mathrm{P}}{\mathrm{T}}=\frac{\mathrm{P}_{\mathrm{B}}}{\mathrm{T}_{\mathrm{B}}}\)
\(
\begin{aligned}
& \frac{75}{300}=\frac{P_B \times 0.008 \times 12.5}{10} \\
& P_B=25 \mathrm{~cm} \text { of } \mathrm{Hg}
\end{aligned}
\)
The distance moved by the mercury,
\(
P_B-P_A=25-12.5=12.5 \mathrm{~cm}
\) -
Question 95 of 102
95. Question
Figure below shows two vessels with adiabatic walls, one containing \(0^{\prime} 1 \mathrm{~g}\) of helium \(\left(\gamma=1.67, M=4 \mathrm{~g} \mathrm{~mol}^{-1}\right)\) and the other containing some amount of hydrogen \(\left(\gamma=1^{-} 4, M=2 \mathrm{~g} \mathrm{~mol}^{-1}\right)\). Initially, the temperatures of the two gases are equal. The gases are electrically heated for some time during which equal amounts of heat are given to the two gases. It is found that the temperatures rise through the same amount in the two vessels. Calculate the mass of hydrogen.
 CorrectIncorrect
CorrectIncorrectHint
Given:
Mass of \(\mathrm{He}, m_{\mathrm{He}}=0.1 \mathrm{~g}\)
\(
\gamma_1=1.67
\)
Molecular weight of \(\mathrm{He}, M_{\mathrm{He}}=4 \mathrm{~g} / \mathrm{mol}\)
\(
\begin{aligned}
& M_{\mathrm{H} 2}=? \\
& M_{\mathrm{H} 2}=2 \mathrm{~g} / \mathrm{mol} \\
& \gamma_2=1.4
\end{aligned}
\)
Since it is an adiabatic environment and the system is not dong any external work, the amount of heat given will be used up entirely to raise its internal energy.
For \(\mathrm{He}, d Q=\mathrm{d} U=n C_v d T \quad \ldots\).. (i)
\(
\begin{aligned}
& =\frac{\mathrm{m}}{4} \times \frac{\mathrm{R}}{\gamma-1} \times \mathrm{dT} \\
& =\frac{0.1}{4} \times \frac{\mathrm{R}}{(1.67-1)} \times \mathrm{dT} \\
& \text { For } \mathrm{H}_2, d Q=\mathrm{d} U=n C v d T \dots(ii)\\
& =\frac{\mathrm{m}}{2} \times \frac{\mathrm{R}}{\gamma-1} \times \mathrm{dT} \\
& =\frac{\mathrm{m}}{2} \times \frac{\mathrm{R}}{1.4-1} \times \mathrm{dT}
\end{aligned}
\)
where \(m\) is the required mass of \(\mathrm{H}_2\).
Since equal amount of heat is given to both gases; so dQ is same in both eq (i) and (ii), we get
\(
\begin{aligned}
& \frac{0.1}{4} \times \frac{\mathrm{R}}{0.67} d T \\
& =\frac{\mathrm{m}}{2} \times \frac{\mathrm{R}}{0.4} \times \mathrm{dT} \\
& =m=\frac{0.1}{2} \times \frac{0.4}{0.67} \\
& \Rightarrow m=0.0298 \approx 0.03 \mathrm{~g}
\end{aligned}
\) -
Question 96 of 102
96. Question
Two vessels \(A\) and \(B\) of equal volume \(V_0\) are connected by a narrow tube which can be closed by a valve. The vessels are fitted with pistons which can be moved to change the volumes. Initially, the valve is open and the vessels contain an ideal gas \(\left(C_p / C_V=\gamma\right)\) at atmospheric pressure \(p_0\) and atmospheric temperature \(T_0\). The walls of the vessel \(A\) are diathermic and those of \(B\) are adiabatic. The valve is now closed and the pistons are slowly pulled out to increase the volumes of the vessels to double the original value. (a) Find the temperatures and pressures in the two vessels. (b) The valve is now opened for sufficient time so that the gases acquire a common temperature and pressure. Find the new values of the temperature and the pressure.
CorrectIncorrectHint
Initial pressure of the gas in both the vessels \(=P_0\)
Initial temperature of the gas in both the vessels \(=\mathrm{T}_0\)
Initial volume \(=\mathrm{V}_0\)
\(
\frac{C_p}{C_v}=\gamma
\)
(a) The temperature inside the diathermic vessel remains constant. Thus,
\(
\begin{aligned}
& P_1 V_1=P_2 V_2 \\
& \Rightarrow P_0 V_0=P_2 \times 2 V_0 \\
& \Rightarrow P_2=\frac{P_0}{2} \\
& \text { temperature }=T_0
\end{aligned}
\)
The temperature inside the adiabatic vessel does not remain constant.
So, for an adiabatic process,
\(
T_1 V_1{ }^{\gamma-1}=T_2 V_2{ }^{\gamma-1}
\)
\(
\begin{aligned}
& \Rightarrow \mathrm{T}_0 \mathrm{~V}_0^{\gamma-1}=\mathrm{T} \times\left(2 \mathrm{~V}_0\right)^{\gamma-1} \\
& \Rightarrow \mathrm{T}_2=\mathrm{T}_0 \times 2^{1-\gamma} \\
& \Rightarrow \mathrm{P}_1 \mathrm{~V}_1^\gamma=\mathrm{P}_2 \mathrm{~V}_2^\gamma \\
& \mathrm{P}_0 \mathrm{~V}_0^\gamma=\mathrm{P}_2 \times\left(2 \mathrm{~V}_0\right)^\gamma \\
& \Rightarrow \mathrm{P}_2=\left(\frac{\mathrm{P}_0}{2^\gamma}\right)
\end{aligned}
\)
(b) When the valves are open, the temperature remains \(T_0\) throughout, i.e. \(T_1=T_2=T_0\).
Also, pressure will be same throughout. Thus, \(P_1=P_2\). As, temperature has not changed on side 1 , so pressure on this side will also not change (volume is also fixed due to fixed piston) and will be equal to \(P_0\) (pressure is an intrinsic variable).
On side 2, pressure will change to accommodate the changes in temperature on this side.
So, \(P_0=P_1+P_2\)
\(
\Rightarrow 2 \mathrm{P}_1=2 \mathrm{P}_2
\)
So, \(P_1=P_2=\frac{P_0}{2}\) -
Question 97 of 102
97. Question
Figure below shows an adiabatic cylindrical tube of volume \(V_0\) divided in two parts by a frictionless adiabatic separator. Initially, the separator is kept in the middle, an ideal gas at pressure \(p_1\) and temperature \(T_1\) is injected into the left part and another ideal gas at pressure \(p_2\) and temperature \(T_2\) is injected into the right part. \(C_p / C_V=\gamma\) is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the two parts, (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.
 CorrectIncorrect
CorrectIncorrectHint
The separator will stop in the position when pressure of both parts of the tube become equal, Let is is \(P\), If \(V_1[latex] and [latex]V_2\) are the volumes of two parts, then \(V_1+V_2=V_0\) (i)
(a) the process in each in each part is adiabatic, so
\(
\begin{aligned}
& P_1\left(\frac{V_0}{2}\right)^\gamma=P V_1^\gamma \text { (ii) } \\
& P_2\left(\frac{V_0}{2}\right)^\gamma=P V_2^\gamma \text { (iii) }
\end{aligned}
\)
Dividing Eq. (i) by Eq. (ii) we have
\(
\begin{aligned}
& \frac{P_1}{P_2}=\frac{V_1^\gamma}{V_2^\gamma} \\
& \text { oг } V_1=\left(\frac{P_1}{P_2}\right)^{1 / \gamma} V_2 \text { (iv) }
\end{aligned}
\)
Substituing this value in Eq. (i) we get
\(
V_2=\left[\frac{V_0 P_2^{1 / \gamma}}{P_1^{1 / \gamma}+P_2^{1 / \gamma}}\right] \text { and } V_1=\left[\frac{V_0 P_1^{1 / \gamma}}{P_1^{1 / \gamma}+P_2^{1 / \gamma}}\right]
\)
(b) (b) Since the whole process takes place in adiabatic surroundings, the separator is adiabatic.
Hence, heat given to the gas in the left part is 0.
(c) There will be a common pressure \(P\) when equilibrium is reached. The slid will move until the pressure on the two sides becomes equal.
\(
P_1 V_1^\gamma+P_2 V_2^\gamma=P V_0^\gamma
\)
For equilibrium, \(\mathrm{V}_1=\mathrm{V}_2=\frac{\mathrm{V}_0}{2}\)
Hence,
\(
\begin{aligned}
& P_1\left(\frac{\mathrm{V}_0}{2}\right)^\gamma+\mathrm{P}_2\left(\frac{\mathrm{V}_0}{2}\right)^\gamma=\mathrm{P}\left(\mathrm{V}_0\right)^\gamma \\
& \text { Or } \mathrm{P}=\left(\frac{\mathrm{P}_1^{\frac{1}{\gamma}}+\mathrm{P}_2^{\frac{1}{\gamma}}}{2}\right)^\gamma
\end{aligned}
\) -
Question 98 of 102
98. Question
An adiabatic cylindrical tube of cross-sectional area \(1 \mathrm{~cm}^2\) is closed at one end and fitted with a piston at the other end. The tube contains \(0.03 \mathrm{~g}\) of an ideal gas. At \(1 \mathrm{~atm}\) pressure and at the temperature of the surrounding, the length of the gas column is \(40 \mathrm{~cm}\). The piston is suddenly pulled out to double the length of the column. The pressure of the gas falls to \(0.355 \mathrm{~atm}\). Find the speed of sound in the gas at atmospheric temperature.
CorrectIncorrectHint
Given:
Area of the tube, \(A=1 \mathrm{~cm}^2=1 \times 10^{-4} \mathrm{~m}^2\)
Mass of the gas, \(M=0.03 \mathrm{~g}=0.03 \times 10^{-3} \mathrm{~kg}\)
Initial pressure, \(\mathrm{P}=1 \mathrm{~atm}=10^5 \mathrm{Pascal}\)
Initial length of the mercury column, \(L=40 \mathrm{~cm}=0.4 \mathrm{~m}\)
Final length of the mercury column, \(L_1=80 \mathrm{~cm}=0.8 \mathrm{~m}\)
Final pressure, \(P^{\prime}=0.355 \mathrm{~atm}\)
The process is adiabatic. So,
\(
\begin{aligned}
& P(V)^\gamma=P^{\prime}\left(V^{\prime}\right)^\gamma \\
& \Rightarrow 1 \times(A \times 0.4)^\gamma=0.355 \times(A \times 0.8)^\gamma \\
& \Rightarrow 1 \times 1=0.355 \times 2^\gamma \\
& \Rightarrow \frac{1}{0.355}=2^\gamma \\
& \gamma \log 2=\log \left(\frac{1}{0.355}\right) \\
& \Rightarrow \gamma=1.4941
\end{aligned}
\)
Speed of sound in the gas,
\(
\begin{aligned}
& \mathrm{v}=\sqrt{\frac{\gamma \mathrm{P}}{\rho}}=\sqrt{\frac{\gamma \mathrm{P}}{\frac{\mathrm{m}}{\mathrm{v}}}} \\
& \mathrm{v}=\sqrt{\frac{1.4941 \times 10^5}{\frac{\mathrm{m}}{\mathrm{v}}}}=\sqrt{\frac{1.4941 \times 10^5}{\frac{0.03 \times 10^{-3}}{10^{-4} \times 1 \times 0.4}}} \\
& \Rightarrow \mathrm{v}=446.33 \approx 447 \mathrm{~m} / \mathrm{s}
\end{aligned}
\) -
Question 99 of 102
99. Question
The speed of sound in hydrogen at \(0^{\circ} \mathrm{C}\) is \(1280 \mathrm{~m} \mathrm{~s}^{-1}\). The density of hydrogen at STP is \(0.089 \mathrm{~kg} \mathrm{~m}^{-3}\). Calculate the molar heat capacities \(C_p\) and \(C_V\) of hydrogen.
CorrectIncorrectHint
Given:
Velocity of sound in hydrogen, \(V=1280 \mathrm{~m} / \mathrm{s}\)
Temperature, \(\mathrm{T}=0^{\circ} \mathrm{C}=273 \mathrm{~K}\)
Density of \(\mathrm{H}_2=0.089 \mathrm{~kg} / \mathrm{m}^3\)
\(\mathrm{R}=8.3 \mathrm{~J} / \mathrm{mol}-\mathrm{K}\)
At STP,
\(
\mathrm{P}=10^5 \mathrm{~Pa}
\)
We know:
\(
\begin{aligned}
& \mathrm{V}_{\text {sound }}=\left(\frac{\sqrt{\gamma \mathrm{p}}}{\rho}\right) \\
& 1280=\sqrt{\frac{\gamma \times 10^5}{0.089}}
\end{aligned}
\)
Or \(\gamma=\frac{1280 \times 1280 \times 0.089}{10^5}\)
\(=1.46\)
\(\frac{C_p}{C_v}=\gamma\) or \(C_p-C_v=R\)
\(C_v=\frac{R}{\gamma-1}=\frac{8.3}{1.46-1}\)
\(=18.0 \mathrm{~J} / \mathrm{mol}-\mathrm{K}\)
\(C_p=\gamma C_v=1.46 \times 18.0\)
\(
=26.28 \approx 26.3 / \mathrm{mol}-\mathrm{K}
\) -
Question 100 of 102
100. Question
\(4.0 \mathrm{~g}\) of helium occupies \(22400 \mathrm{~cm}^3\) at STP. The specific heat capacity of helium at constant pressure is \(5 \cdot 0 \mathrm{cal} \mathrm{K}^{-1} \mathrm{~mol}^{-1}\). Calculate the speed of sound in helium at STP.
CorrectIncorrectHint
Given:
Specific heat capacity at constant pressure, \(C_p=5.0 \mathrm{cal} / \mathrm{mol}-\mathrm{K}\)
\(
\begin{aligned}
& C_p=5.0 \times 4.2 \mathrm{~J} / \mathrm{mol}-\mathrm{K} \\
& C_p=21 \mathrm{~J} / \mathrm{mol}-\mathrm{K}
\end{aligned}
\)
Volume of helium, \(V=22400 \mathrm{~cm}^3=0.0224 \mathrm{~m}^3\)
At STP, \(P=1 \mathrm{~atm}=10^5 \mathrm{~Pa}\)
The speed of sound in gas,
\(
\begin{aligned}
& \mathrm{v}=\sqrt{\frac{\gamma \mathrm{p}}{\rho}}=\sqrt{\frac{\gamma \mathrm{RT}}{\mathrm{M}}}=\sqrt{\frac{\gamma \mathrm{PV}}{\mathrm{M}}} \\
& C_p=\frac{\mathrm{R} \gamma}{\gamma-1} \\
& \text { Or } 21(\gamma-1)=8.3 \gamma \\
& \Rightarrow 21 \gamma-8.3 \gamma=21 \\
& \Rightarrow 12.7 \gamma=21 \\
& \therefore \gamma=\frac{21}{12.7}=1.653 {v}=\sqrt{\frac{1.653 \times 1.0 \times 10^5 \times 0.0224}{4 \times 10^{-3}}} \\
& v=960 \mathrm{~m} / \mathrm{s}
\end{aligned}
\) -
Question 101 of 102
101. Question
An ideal gas having density \(1.7 \times 10^{-3} \mathrm{~g} \mathrm{~cm}^{-3}\) at a pressure \(1.5 \times 10^6 \mathrm{~Pa}\) is filled in a Kundt tube. When the gas is resonated at a frequency of \(3.0 \mathrm{kHz}\), nodes are formed at a separation of \(6.0 \mathrm{~cm}\). Calculate the molar heat capacities \(C_p\) and \(C_V\) of the gas.
CorrectIncorrectHint
Given:
Density of the ideal gas, \(\rho=1.7 \times 10^{-3} \mathrm{~g} / \mathrm{cm}^3\) \(=1.7 \mathrm{k} / \mathrm{gm}^3\)
Pressure of the gas, \(P=1.5 \times 10^5 \mathrm{~Pa}\), \(\mathrm{R}=8.3 \mathrm{~J} / \mathrm{mol}-\mathrm{K}\)
Resonance frequency of the gas \(=3.0 \mathrm{kHz}\)
Node separation in the Kundt’s tube
\(
\frac{\mathrm{l}}{2}=6 \mathrm{~cm}
\)
So, \(\mathrm{l}=2 \times 6=12 \mathrm{~cm}=12 \times 10^{-2} \mathrm{~m}\)
So, \(\mathrm{V}=f \times l=3 \times 10^3 \times 12 \times 10^{-2}\)
\(=360 \mathrm{~m} / \mathrm{s}\)
Speed of sound, \(V=\sqrt{\frac{\gamma p}{\rho}}\)
\(
\begin{aligned}
& \text { Or } V^2=\frac{\gamma p}{\rho} \\
& \therefore \gamma=\frac{v^2 \rho}{P}=\frac{(360)^2 \times 1.7 \times 10^{-3}}{1.5 \times 10^5} \\
& =1.4688
\end{aligned}
\)
Using \(C_p-C_v=R\) and \(\frac{C_p}{C_v}=\gamma\)
We know that
\(
\begin{aligned}
& C_v=\frac{R}{\gamma-1}=\frac{8.3}{0.4688} \\
& =17.7 \mathrm{~J} / \mathrm{mol}-\mathrm{K} \\
& C_p=R+C_v=8.3+17.7=26 \mathrm{~J} / \mathrm{mol}-\mathrm{K}
\end{aligned}
\) -
Question 102 of 102
102. Question
Standing waves of frequency \(5.0 \mathrm{kHz}\) are produced in a tube filled with oxygen at \(300 \mathrm{~K}\). The separation between the consecutive nodes is \(33 \mathrm{~cm}\). Calculate the specific heat capacities \(C_p\) and \(C_V\) of the gas.
CorrectIncorrectHint
Frequency of standing waves, \(\mathrm{f}=5 \times 10^3 \mathrm{~Hz}\)
Temperature of oxygen, \(T=300 \mathrm{~K}\)
From Kundt’s tube theory, we know that \(\frac{l}{2}=\) node separation \(=3.3 \mathrm{~cm}\)
\(\therefore \mathrm{l}=6.6 \times 10^{-2} \mathrm{~m}\)
Also,
\(
\begin{aligned}
& \mathrm{v}=f \times l=5 \times 10^3 \times 6.6 \times 10^{-2} \\
& =(66 \times 5)=330 \mathrm{~m} / \mathrm{s} \\
& \mathrm{v}=\sqrt{\frac{\gamma \mathrm{RT}}{\mathrm{M}}} \\
& \mathrm{v}^2=\frac{\gamma \mathrm{RT}}{\mathrm{M}} \\
& \therefore \gamma=\frac{330 \times 330 \times 32}{8.3 \times 300 \times 100}=1.3995
\end{aligned}
\)
Specific heat at constant volume, \(C_v=\frac{R}{\gamma-1}=\frac{8.3}{0.3995}\)
\(
=20.7 \mathrm{~J} \mathrm{~mol}-\mathrm{K}
\)
Specific heat at constant pressure, \(C_p=C_v+R\)
\(
\begin{aligned}
& C_p=20.7+8.3 \\
& C_p=29.0 \mathrm{~J} / \mathrm{mol}-\mathrm{K}
\end{aligned}
\)