Exemplar MCQs
Quiz Summary
0 of 88 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 88 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 88
1. Question
A bimetallic strip is made of aluminium and steel \(\left(\alpha_{A l}>\alpha_{\text {steel }}\right)\). On heating, the strip will
CorrectIncorrectHint
Bi-metallic strip- Two strips of equal lengths but of different materials (different coefficient of linear expansion) when join together, it is called “bi-metallic strip”, and can be used in thermostat to break or make electrical contact. This strip has the characteristic property of bending on heating due to unequal linear expansion of the two metal. The strip will bend with metal of greater a on outer side, i.e. convex side.
On heating, the metallic strip with higher coefficient of linear expansion \(\left(\alpha_{\mathrm{Al}}\right)\) will expand more. According to the question, \(\propto_{\mathrm{Al}}>\alpha_{\text {steel, }}\) so aluminum will expand more. So, it should have larger radius of curvature. Hence, aluminium will be on convex side. The metal of smaller \(\propto\) (i.e., steel) bends on the inner side, i.e., concave side.
-
Question 2 of 88
2. Question
A uniform metallic rod rotates about its perpendicular bisector with the constant angular speed. If it is heated uniformly to raise its temperature slightly
CorrectIncorrectHint
(b) When the rod is heated uniformly to raise its temperature slightly, it expands. So, moment of inertia of the rod will increase.Moment of inertia of a uniform rod about its perpendicular bisector,
\(
I=\frac{1}{12} M L^2
\)
\(\Delta T=\) Increase in the temperature of the rod.
\(\therefore \quad\) Changed length, \(L^{\prime}=L(1+\alpha \Delta T) \dots(i)\)
\(\therefore\) New moment of inertia of rod,
\(
\begin{aligned}
I^{\prime} & =\frac{M L^{\prime 2}}{12}=\frac{M}{12} L[1+\alpha \Delta T]^2 \\
& =\frac{M L^2}{12}\left[1+2 \alpha \Delta T+\alpha^2(\Delta T)^2\right] \\
\therefore \quad I^{\prime} & =I[1+2 \alpha \Delta T]
\end{aligned}
\)
[Using (i)]
\(\left(\because \alpha^2(\Delta T)^2\right.\) is very small)
If the temperature increases, moment of inertia will increase.
No external torque is acting on the system, so angular momentum should be conserved.
\(\quad L=\) Angular momentum \(=I \omega=\) constant
\(\Rightarrow \quad I^{\prime} \omega^{\prime}=I \omega\)
where, \(I=\) initial M.I. of rod before heating
\(\omega=\) initial angular velocity
\(I^{\prime}=\) final M.I after heating
\(\omega^{\prime}=\) final angular velocity after heating
Due to expansion of the rod \(I^{\prime}>I\).
\(\Rightarrow \quad \frac{\omega^{\prime}}{\omega^{\prime}}=\frac{I}{I^{\prime}}<1\)
\(\Rightarrow \quad \omega^{\prime}<\omega\)
So, angular velocity (speed of rotation) decreases. -
Question 3 of 88
3. Question
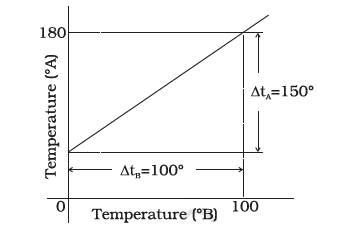
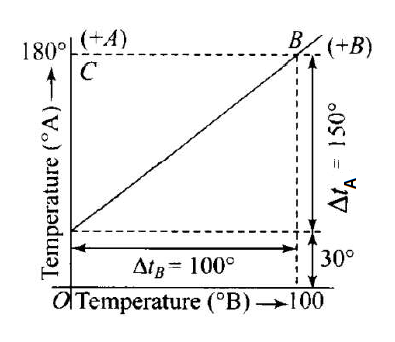
The graph between two temperature scales A and B is shown in the figure below Between upper flxed point and lower flxed point there are 150 equal division on scale A and 100 on scale B. The relationship for conversion between the two scales is given by
 CorrectIncorrect
CorrectIncorrectHint
The temperature on one scale can be converted into other scales by using the following identity.
Reading on any scale – LFP/UFP – LFP = Constant for all scales
Where LFP → Lower fixed point
UFP \(\rightarrow\) Upper fixed point
From the graph, it is clear that the lowest point for scale \(\mathrm{A}\) is \(30^{\circ}\) and the highest point for scale \(\mathrm{A}\) is \(180^{\circ}\).
The lowest point for scale \(B\) is \(0^{\circ}\) and the highest point for scale \(B\) is \(100^{\circ}\). Hence, the relation between the two scales \(A\) and \(B\) is given by
\(
\begin{aligned}
& \frac{T_A-(L F P)_A}{(U F P)_A-(L F P)_A}=\frac{T_B-(L F P)_B}{(U F P)_B-(L F P)_B} \\
& \Rightarrow \frac{T_A-30}{180-30}=\frac{T_B-0}{100-0} \\
& \Rightarrow \frac{t_A-30}{150}=\frac{t_B}{100}
\end{aligned}
\)
-
Question 4 of 88
4. Question
An aluminium sphere is dipped into water. Which of the following is true?
CorrectIncorrectHint
Key concept: Liquids generally increase in volume with increasing temperature but in case of water, it expands on heating if its temperature is greater than \(4^{\circ} \mathrm{C}\). The density of water reaches a maximum value of \(1.000 \mathrm{~g} / \mathrm{cm} 3\) at \(4^{\circ} \mathrm{C}\)
This behaviour of water in the range from \(0^{\circ} \mathrm{C}\) to \(4^{\circ} \mathrm{C}\) is called anomalous expansion.
Let volume of the sphere be \(V\) and \(\rho\) be its density, then we can write buoyant force at \(0^{\circ} \mathrm{C}\).
\(F_{0^{\circ} \mathrm{C}}=V \rho_{0^{\circ}} \mathrm{g} \quad\left(\rho_{0^{\circ}}=\right.\) density at \(\left.0^{\circ} \mathrm{C}\right)\)
Buoyancy at \(4^{\circ} \mathrm{C}\)
\(
\begin{aligned}
& F_{4^{\circ} \mathrm{C}}=V \rho_{4^{\circ} \mathrm{C}} \\
\Rightarrow \quad & \frac{F_{4^{\circ} \mathrm{C}}}{F_{0^{\circ} \mathrm{C}}}=\frac{\rho_{4^{\circ} \mathrm{C}}}{\rho_{0^{\circ} \mathrm{C}}}>1 \\
\Rightarrow \quad & F_{4^{\circ} \mathrm{C}}>F_{0^{\circ} \mathrm{C}}
\end{aligned} \quad\left(\because \rho_{4^{\circ} \mathrm{C}}>\rho_{0^{\circ} \mathrm{C}}\right)
\)
Hence, buoyancy will be less in water at \(0^{\circ} \mathrm{C}\) than that in water at \(4^{\circ} \mathrm{C}\). -
Question 5 of 88
5. Question
As the temperature is increased, the time period of a pendulum
CorrectIncorrectHint
(a) A pendulum clock keeps proper time at temperature \(\theta_0\). If temperature is increased to \(\theta\left(>\theta_0\right)\), then due to linear expansion, length of pendulum increases and hence its time period will increase
Let \(T=2 \pi \sqrt{\frac{L_0}{g}}\) at temperature \(\theta_0\) and \(T^{\prime}=2 \pi \sqrt{\frac{L}{g}}\) at temperature \(\theta\).
\(
\frac{T^{\prime}}{T}=\sqrt{\frac{L^{\prime}}{L}}=\sqrt{\frac{L[1+\alpha \Delta \theta]}{L}}=1+\frac{1}{2} \alpha \Delta \theta
\)
Therefore change (loss or gain) in time per unit time lapsed is \(\frac{T^{\prime}-T}{T}=\frac{1}{2} \alpha \Delta \theta\) Fractional change in time period \(\frac{\Delta T}{T}=\frac{1}{2} \alpha \Delta \theta\)
So, as the temperature increases, length of pendulum increases and hence time period of pendulum increases. Due to increment in its time period, a pendulum clock becomes slow in summer and will lose time.
-
Question 6 of 88
6. Question
Heat is associated with
CorrectIncorrectHint
(a) When a body is heated its temperature rises and in liquids and gases vibration of molecules about their mean position increases, hence kinetic energy associated with random motion of molecules increases. So, thermal energy or heat associated with the random and translatory motions of molecules.
-
Question 7 of 88
7. Question
The radius of a metal sphere at room temperature \(T\) is \(R\), and the coefficient of linear expansion of the metal is \(\alpha\). The sphere is heated a little by a temperature \(\Delta T\) so that its new temperature is \(T+\Delta T\). The increase in the volume of the sphere is approximately
CorrectIncorrectHint
Key concept: The co-efficient \(\alpha, \beta\) and \(\gamma\) for a solid are related to each other as follows:
\(
\alpha=\frac{\beta}{2}=\frac{\gamma}{3} \Rightarrow \alpha: \beta: \gamma=1: 2: 3
\). The values of \(\alpha, \beta\) and \(\gamma\) are independent of the units of length, area and volume respectively. For anisotropic solids \(\gamma=\alpha_x+\alpha_y+\alpha_z\) where \(\alpha_x, \alpha_y\) and \(\alpha_z\) represent the mean coefficients of linear expansion along three mutually perpendicular directions.
As the temperature increases radius of the sphere increases as shown. So, the volume of the sphere increases.
Original volume of the sphere \(V_0=\frac{4}{3} \pi R^3\)
Coefficient of linear expansion \(=\alpha\)
Hence, coefficient of volume expansion \(=3 \alpha\)
\(\therefore \quad\) Change in volume is \(\Delta V=V_0 \gamma \Delta T\)
\(
\Delta V=\frac{4}{3} \pi R^3(3 \alpha) \Delta T
\)
Increase in volume \(=4 \pi R^3 \alpha \Delta T\)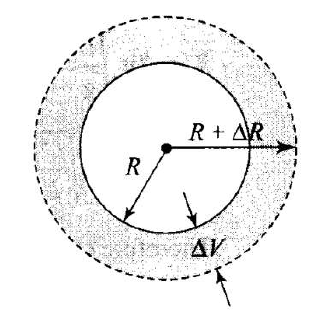
-
Question 8 of 88
8. Question
A sphere, a cube and a thin circular plate, all of same material and same mass are initially heated to same high temperature.
CorrectIncorrectHint
\(
\rho=\text { mass } / \text { volume }
\)So, the volume of all object will also be same. Here the cooling will be done in the form of radiations that is according to Stefan’s law. Since, emissive power is directly proportional to the surface. Here, for given volume, sphere has least surface area and circular plate of greatest surface area.
As thickness of the plate is least, hence surface area of the plate is maximum. According to Stefan’s law, heat loss (cooling) is directly proportional to the surface area.
\(H_{\text {sphere }}: H_{\text {cube }}: H_{\text {plate }}=A_{\text {sphere }}: A_{\text {cube }}: A_{\text {plate }}\)
As \(\mathrm{A}_{\text {plate }}\) is maximum, hence the plate will cool fastest.
As the sphere is having minimum surface area, hence the sphere cools slowest.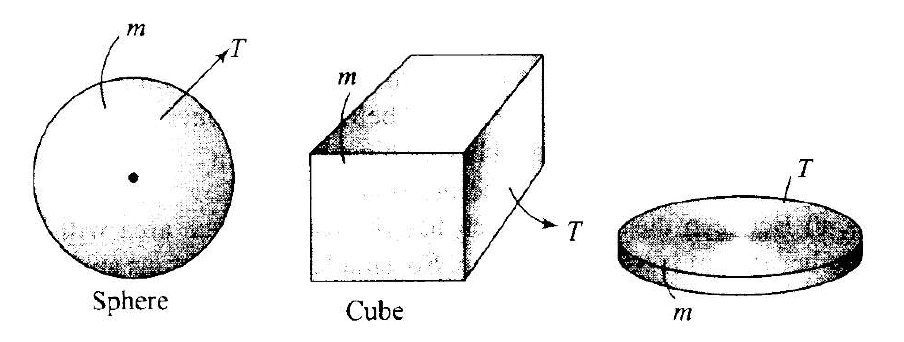
-
Question 9 of 88
9. Question
Mark the correct options:
CorrectIncorrectHint
Key concept:Two bodies are said to be in thermal equilibrium with each other, when no heat flows from one body to the other. That is when both the bodies are at the same temperature.
According to the problem,
(b) If two systems \(X\) and \(Y\) are in thermal equilibrium, i.e., \(T_x=T_y\) and \(x\) is not in thermal equilibrium with \(z\),
i.e., \(T_x \neq T_z\)
then clearly, \(T_y \neq T_z\)
Hence, \(y\) and \(z\) are not in thermal equilibrium.
(d) if \(X\) is not in thermal equilibrium with \(Y\), i.e, \(T_x \neq T_y\) and also \(X\) is not in thermal equilibrium with \(Y\), i.e., \(T_x \neq T_z\)
Then we cannot say about equilibrium of \(Y\) and \(Z\), they may or may not be in equilibrium. -
Question 10 of 88
10. Question
‘Gulab Jamuns’ (assumed to be spherical) are to be heated in an oven. They are available in two sizes, one twice bigger (in radius) than the other. Pizzas (assumed to be discs) are also to be heated in oven. They are also in two sizes, one twice big (in radius) than the other. All four are put together to be heated to oven temperature. Choose the correct option from the following:
CorrectIncorrectHint
(b, c) Between these four which has the least surface area will be heated first because of less heat radiation. So, smaller gulab jamuns are having least surface area, hence they will be heated first.
Similarly, smaller pizzas are heated before bigger ones because they are of small surface areas. -
Question 11 of 88
11. Question
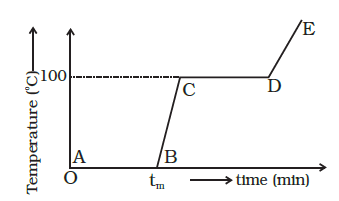
Refer to the plot of temperature versus time (Figure below) showing the changes in the state of ice on heating (not to scale). Which of the following is correct?
 CorrectIncorrect
CorrectIncorrectHint
\((a, d)\) During phase change process, the temperature of the system remains constant.
(a) In region AB, a phase change takes place, heat is supplied and ice melts but the temperature of the system is \(0^{\circ} \mathrm{C}\). it remains constant during process. The heat supplied is used to break bonding between molecules.
(d) In region \(C D\), again a phase change takes place from a liquid to a vapour state during which temperature remains constant. It shows water and steam are in equilibrium at boiling point. -
Question 12 of 88
12. Question
A glass full of hot milk is poured on the table. It begins to cool gradually. Which of the following is correct?
CorrectIncorrectHint
(b, c, d) When hot milk spread on the table heat is transferred to the surroundings by conduction, convection and radiation. Because the surface area of poured milk on a table is more than the surface area of milk filled in a glass. Hence, its temperature falls off exponentially according to Newton’s law of cooling. Heat also will be transferred from surroundings to the milk but will be lesser than that of transferred from milk to the surroundings. So, option (b), (c) and (d) are correct.
-
Question 13 of 88
13. Question
Is the bulb of a thermometer made of diathermic or adiabatic wall?
CorrectIncorrectHint
The bulb of a thermometer is made up of diathermic wall because diathermic walls allow the exchange of heat energy between two systems but adiabatic walls do not. So it receives heat from the body to measure the temperature of the body.
-
Question 14 of 88
14. Question
A student records the initial length \(l\), change in temperature \(\Delta T\) and change in length \(\Delta l\) of a rod as follows:
\(
\begin{array}{cccc}
\text { S.No. } & l(\mathrm{~m}) & \Delta T(\mathrm{C}) & \Delta l(\mathrm{~m}) \\
\hline 1 . & 2 & 10 & 4 \times 10^{-4} \\
2 . & 1 & 10 & 4 \times 10^{-4} \\
3 . & 2 & 20 & 2 \times 10^{-4} \\
4 . & 3 & 10 & 6 \times 10^{-4}
\end{array}
\)If the first observation is correct, what are the other correct observations from 2, 3, and 4.
CorrectIncorrectHint
If the first observation is correct, hence from the 1 st observation we get the coefficient of linear expansion
\(
\alpha=\frac{\Delta l}{l \times \Delta T}=\frac{4 \times 10^{-4}}{2 \times 10}=2 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}
\)
For 2nd observation, \(\Delta l=\alpha l \Delta T\)
\(
\begin{aligned}
& =2 \times 10^{-5} \times 1 \times 10 \\
& =2 \times 10^{-4} \mathrm{~m} \neq 4 \times 10^{-4} \mathrm{~m}
\end{aligned}
\)
which is incorrect.
For 3rd observation, \(\Delta l=\alpha l \Delta T\)
\(
\begin{aligned}
& =2 \times 10^{-5} \times 2 \times 20 \\
& =8 \times 10^{-4} \mathrm{~m} \neq 2 \times 10^{-4} \mathrm{~m}
\end{aligned}
\)
which is incorrect.For 4th observation, \(\Delta l=\alpha l \Delta T\)
\(=2 \times 10^{-5} \times 3 \times 10=6 \times 10^{-4} \mathrm{~m}\) [i.e., observed value is correct] -
Question 15 of 88
15. Question
Why does a metal bar appear hotter than a wooden bar at the same temperature?
CorrectIncorrectHint
The rate of transferring heat in metal is larger than that in wood, as the conductivity of the metal bar is extremely high as compared to wood. Also, metal requires exceedingly small quantities of heat than wood to change temperature as the specific heat of metal is exceptionally low as compared to the wood. Thus, due to larger conductivity and smaller specific heat metal becomes colder and hotter than wood when kept in cold and hot regions, respectively.
Thus if \(a_{\text {practical }}\) and \(E_{\text {practical }}\) represent the absorptive and emissive power of a given surface, while \(a_{\text {black }}\) and \(E_{\text {black }}\) for a perfectly black body, then according to law \(\frac{E_{\text {practical }}}{a_{\text {practical }}}=\frac{E_{\text {biack }}}{a_{\text {black }}}\)
But for a perfectly black body \(a_{\text {black }}=1\), so \(\frac{E_{\text {practical }}}{a_{\text {practical }}}=E_{\text {black }}\)
If emissive and absorptive powers are considered for a particular wavelength \(\lambda,\left(\frac{E_\lambda}{a_\lambda}\right)_{\text {practical }}=\left(E_\lambda\right)_{\text {black }}\)Now since \(\left(E_\lambda\right)_{\text {Black }}\) is constant at a given temperature, according to this law if a surface is a good absorber of a particular wavelength it is also a good emitter of that wavelength. This in turn implies that a good absorber is a good emitter (or radiator). The conductivities of metals are very high compared to wood. Due to the difference in conductivity, if one touch the hot metal with a finger, heat from the surrounding flows faster to the finger from metals and so one feels the heat. Similarly, when one touches a cold metal the heat from the finger flows away to the surroundings faster. So we can say that a good radiator can be a good absorber.
-
Question 16 of 88
16. Question
Calculate the temperature which has the same numeral value on the celsius and Fahrenheit scale.
CorrectIncorrectHint
To construct a scale of temperature, two fixed points are taken. First fixed point is the freezing point of water, it is called lower fixed point. The second fixed point is the boiling point of water, it is called upper fixed point. Temperature on one scale can be converted into other scale by using the following identity.
\(\frac{\text { Reading on any scale }-\text { (LFP) }}{(UFP) – (LFP)}=\) Constant for all scales
\(
\frac{C-0}{100}=\frac{F-32}{212-32}
\)
Let \(T\) be the value of temperature having same value on Celsius and Fahrenheit scale, i.e. \(F=C=T\)
\(
\begin{array}{ll}
& \frac{T-32}{180}=\frac{T}{100} \\
\Rightarrow \quad & T-32=\frac{9}{5} T \Rightarrow \frac{4}{5} T=-32 \\
\Rightarrow \quad & T=-40^{\circ} \mathrm{C}=-40^{\circ} \mathrm{F}
\end{array}
\) -
Question 17 of 88
17. Question
These days people use steel utensils with copper bottom. This is supposed to be good for uniform heating of food. Explain this effect using the fact that copper is the better conductor.
CorrectIncorrectHint
The copper bottom of the steel utensil gets heated quickly.
Because of the reason that copper is a good conductor of heat as compared to steel. But steel does not conduct as quickly, thereby allowing food inside to get heated uniformly.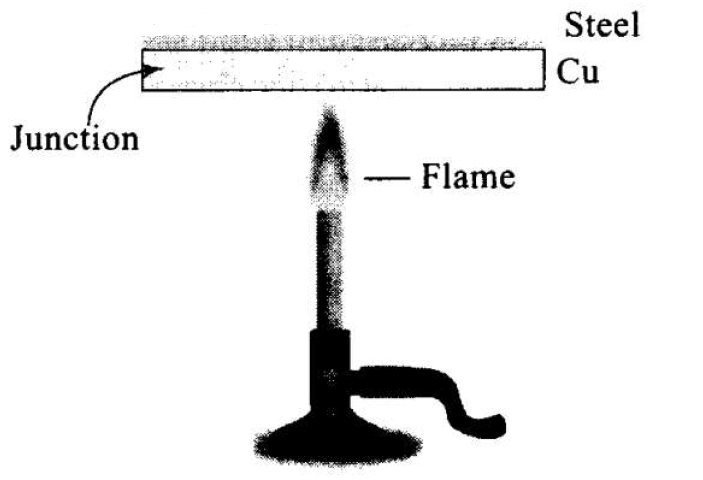
-
Question 18 of 88
18. Question
Find out the increase in moment of inertia \(I\) of a uniform rod (coefficient of linear expansion \(\alpha\) ) about its perpendicular bisector when its temperature is slightly increased by \(\Delta T\).
CorrectIncorrectHint
\(
\text { Moment of inertia of a uniform rod of mass } \mathrm{M} \text { and length } {l} \text { about its perpendicular bisector }
\)
\(
I=\frac{1}{12} M l^2
\)
Increase in length of the rod when temperature is increased by \(\Delta t\), is given by \(L^{\prime}=L(1+\alpha \Delta T)\)
\(\therefore\) New moment of inertia of the rod
\(
\begin{aligned}
I^{\prime} & =\frac{M L^{\prime 2}}{12}=\frac{M}{12} L^2[1+\alpha \Delta T]^2 \\
& =\frac{M L^2}{12}\left[1+2 \alpha \Delta T+\alpha^2(\Delta T)^2\right]
\end{aligned}
\)
\(\therefore\) As change in length \(\Delta l\) is very small, therefore, neglecting \((\Delta l)^2\) \(\left(\because \alpha^2(\Delta T)^2\right.\) is very small) we get
\(
I^{\prime}=I[1+2 \alpha \Delta T]
\)
\(\therefore\) Increase in moment of inertia
\(
=I^{\prime}-I=I[1+2 \alpha \Delta T]-I=2 \alpha I \Delta T
\) -
Question 19 of 88
19. Question
\(100 \mathrm{~g}\) of water is supercooled to \(-10^{\circ} \mathrm{C}\). At this point, due to some disturbance mechanised or otherwise some of it suddenly freezes to ice. What will be the temperature of the resultant mixture and how much mass would freeze?
\(
\left[\mathrm{S}_{\mathrm{w}}=1 \mathrm{cal} / \mathrm{g} /{ }^{\circ} \mathrm{C} \text { and } L^{\mathrm{w}}{ }_{\text {Fuslon }}=80 \mathrm{cal} / \mathrm{g}\right]
\)CorrectIncorrectHint
According to the problem, mass of water \((m)=100 \mathrm{~g}\)
Change in temperature \(\Delta T=0-(-10)=10^{\circ} \mathrm{C}\)
Specific heat of water \(\left(S_{\mathrm{n}}\right)=1 \mathrm{cal} / \mathrm{g} /{ }^{\circ} \mathrm{C}\)
Latent heat of fusion of water \(L^w\) fusion \(=80 \mathrm{cal} / \mathrm{g}\)
Amount of heat required to change the temperature of \(100 \mathrm{~g}\) of water at \(-10^{\circ} \mathrm{C}\) to \(0^{\circ} \mathrm{C}\)
\(
\begin{aligned}
Q & =m S_w \Delta T \\
& =100 \times 1 \times[0-(-10)]=1000 \mathrm{cal}
\end{aligned}
\)
Let \(m\) gram of ice be melted.
\(
\begin{array}{ll}
\therefore & Q=m L \\
\text { or } & m=\frac{Q}{L}=\frac{1000}{80}=12.5 \mathrm{~g}
\end{array}
\)
As small mass of ice is melted, thus the temperature of the resultant mixture will remain \(0^{\circ} \mathrm{C}\) which contains \(12.5 \mathrm{~g}\) of ice and \(87.5 \mathrm{~g}\) of water. -
Question 20 of 88
20. Question
One day in the morning, Ramesh filled up 1/3 bucket of hot water from geyser, to take bath. The remaining 2/3 was to
be filled by cold water (at room temperature) to bring mixture to a comfortable temperature. Suddenly Ramesh
had to attend to something which would take some times, say 5-10 minutes before he could take bath. Now he had
two options: (i) fill the remaining bucket completely by cold water and then attend to the work, (ii) first attend to the
work and fill the remaining bucket just before taking bath. Which option do you think would have kept the water warmer?CorrectIncorrectHint
According to the Newton’s law of cooling, the rate of loss of heat is directly proportional to the difference of temperature. Or we can say which gives a consequence about rate of fall of temperature of a body with respect to the difference of temperature of body and surroundings.
The first option would have kept water warmer because by adding hot water to cold water, the temperature of the mixture decreases. Due to this temperature difference between the mixed water in the bucket and the surrounding decreases, thereby the decrease in the rate of loss of the heat by the water.
In second option, the hot water in the bucket will lose heat quickly. So if he first attend to the work and fill the remaining bucket with cold water which already lose much heat in 5-10 minutes then the water become more colder as compared with first case. -
Question 21 of 88
21. Question
We would like to prepare a scale whose length does not change with temperature. It is proposed to prepare a unit scale of this type whose length remains, say \(10 \mathrm{~cm}\). We can use a bimetallic strip made of brass and iron each of different length whose length (both components) would change in such a way that difference between their lengths remain constant. If \(\alpha_{\text {tran }}=1.2 \times 10^{-5} / \mathrm{K}\) and \(\alpha_{\text {brass }}=1.8 \times 10^{-5} / \mathrm{K}\), what should we take as length of each strip?
CorrectIncorrectHint
According to the problem, \(L_I-L_b=10 \mathrm{~cm}\) where,
\(L_I=\) length of iron scale
\(L_b=\) Length of brass scale
This condition is possible if change in length both the rods is remain same at all temperatures.
Change in length of iron rod,
\(
\Delta L=\alpha_I L_I \Delta T
\)
Change in length of brass rod,
\(
\Delta L=\alpha_B L_B \Delta T
\)
As the change will equal in both the rods, so
\(
\begin{array}{ll}
& \alpha_I L_I \Delta T=\alpha_B L_B \Delta T \\
\Rightarrow & \alpha_I L_I=\alpha_B L_B \Rightarrow \frac{L_I}{L_B}=\frac{\alpha_B}{\alpha_I} \\
\text { Here, } & \alpha_B=1.8 \times 10^{-5} \mathrm{~K}^{-1}, \alpha_I=1.2 \times 10^{-5} \mathrm{~K}^{-1} \\
\therefore & \frac{L_I}{L_B}=\frac{1.8 \times 10^{-5}}{1.2 \times 10^{-5}}=\frac{3}{2} \\
& L_I=\frac{3}{2} L_B \\
\text { As, } & L_I-L_B=10 \mathrm{~cm}
\end{array}
\)
\(
\frac{3}{2} L_B-L_B=10 \Rightarrow \frac{1}{2} L_B=10 \Rightarrow L_B=20 \mathrm{~cm}
\) -
Question 22 of 88
22. Question
We would like to make a vessel whose volume does not change with temperature. We can use brass and 1ron \(\left(\beta_{\text {vbrass }}=6 \times 10^{-5} / \mathrm{K}\right.\) and \(\beta_{\text {viron }}=3.55 \times 10^{-5} /\) K) to create a volume of \(100 \mathrm{cc}\). How do you think you can achieve this?
CorrectIncorrectHint
Here we are making a vessel whose Brass volume does not change with temperature.
To make the desired vessel, we should have an iron vessel with a brass rod inside as shown in the diagram.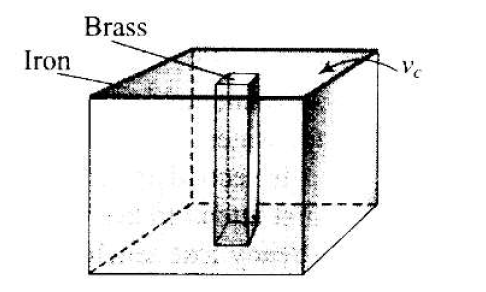
Volume of vessel, \(V_0=100 \mathrm{~cm}^3\) \(=10^{-4}=\) constant
Volume of iron vessel \(\left(V_I\right)\) – Volume of brass \(\operatorname{rod}\left(V_B\right)=10^{-4} \mathrm{~m}^3\)
\(
\Rightarrow \quad V_I-V_B=10^{-4} \mathrm{~m}^3 \dots(i)
\)
This condition is possible if
\(
\begin{array}{ll}
& \beta_I V_I \Delta T=\beta_B V_B \Delta T \\
\therefore & V_I=\left(\frac{\beta_B}{\beta_I}\right) V_B=\left(\frac{6 \times 10^{-5}}{3.55 \times 10^{-5}}\right) V_B=1.69 V_B
\end{array}
\)
From equation (i),
\(
\begin{array}{ll}
& 1.69 V_B-V_B=10^{-4} \\
\Rightarrow \quad & V_B=\frac{10^{-4}}{0.69}=1.449 \times 10^{-4} \mathrm{~m}^3 \\
\Rightarrow \quad & V_B=144.9 \mathrm{~cm}^3 \\
& V_I=1.69 V_B=1.69 \times 144.9=244.9 \mathrm{~cm}^3
\end{array}
\)
Therefore, an iron vessel with a volume of \(249.9 \mathrm{~cm}^3\) fitted with a brass rod of volume \(144.9 \mathrm{~cm}^3\) will serve as a vessel of volume \(100 \mathrm{~cm}^3\), which will not change with temperature.
Important points:
– Solids can expand in one dimension (linear expansion), two dimensions (superficial expansion) and three dimensions (volume expansion) while liquids and gases usually suffers change in volume only.
– Thermal expansion is minimum in case of solids but maximum in case of gases because intermoleeular force is maximum in solids but minimum in gases. -
Question 23 of 88
23. Question
Calculate the stress developed inside a tooth cavity filled with copper when hot tea at temperature of \(57^{\circ} \mathrm{C}\) is drunk. You can take body (tooth) temperature to be \(37^{\circ} \mathrm{C}\) and \(\alpha=1.7 \times 10^{-5} /{ }^{\circ} \mathrm{C}\), bulk modulus for copper \(=140 \times 10^9 \mathrm{~N} / \mathrm{m}^2\).
CorrectIncorrectHint
According to the problem, decrease in temperature
\(
(\Delta t)=57-37=20^{\circ} \mathrm{C}
\)
Coefficient of linear expansion
\(
(\alpha)=1.7 \times 10^{-5} /{ }^{\circ} \mathrm{C}
\)
Bulk modulus for copper \((B)=140 \times 10^9 \mathrm{~N} / \mathrm{m}^2\)
Coefficient of cubical expansion
\(
(\gamma)=3 \alpha=5.1 \times 10^{-5} /{ }^{\circ} \mathrm{C}
\)
Let initial volume of the cavity be \(V\) and its volume increases by \(\Delta V\) due to increase in temperature.
\(
\therefore \quad \Delta V=\gamma V \Delta t \Rightarrow \frac{\Delta V}{V}=\gamma \Delta t
\)
We know, \(B=\frac{\text { stress }}{\text { volume strain }}\)
\(
\begin{aligned}
\therefore \quad \text { Thermal stress }=B \times\left(\frac{\Delta V}{V}\right) & =B(\gamma \Delta T) \\
& =B(3 \alpha \Delta T) \quad(\because \gamma=3 \alpha) \\
& =140 \times 10^9 \times 3 \times 1.7 \times 10^{-5} \times 20 \\
& =1.428 \times 10^8 \mathrm{Nm}^{-2}
\end{aligned}
\)
This is about \(10^3\) times of atmospheric pressure. -
Question 24 of 88
24. Question
A rail track made of steel having length \(10 \mathrm{~m}\) is clamped on a ratllway line at its two ends (Figure below). On a summer day due to rise in temperature by \(20^{\circ} \mathrm{C}\), it is deformed as shown in figure. Find \(x\) (displacement of the centre) if \(\alpha_{\text {steel }}=1.2 \times 10^{-5} /{ }^{\circ} \mathrm{C}\).
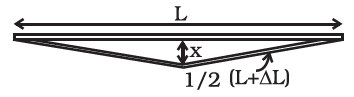 CorrectIncorrect
CorrectIncorrectHint
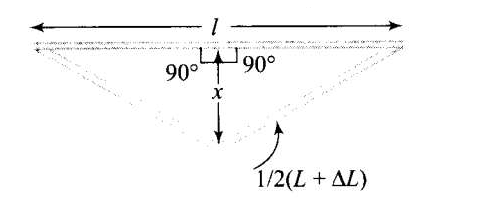
\(
\text { Diagram shows the deformation of a railway track due to rise in temperature. }
\)
\(
\alpha_{\text {steel }}=1.2 \times 10^{-5} /{ }^{\circ} \mathrm{C}
\)
Applying Pythagoras theorem in right angled triangle,
\(
\begin{aligned}
x^2 & =\left(\frac{L+\Delta L}{2}\right)^2-\left(\frac{L}{2}\right)^2 \\
\Rightarrow \quad x & =\sqrt{\left(\frac{L+\Delta L}{2}\right)^2-\left(\frac{L}{2}\right)^2} \\
& =\sqrt{\left(\frac{L}{2}\right)^2+\frac{2 L \Delta L}{4}+\left(\frac{\Delta L}{2}\right)^2-\left(\frac{L}{2}\right)^2} \\
& =\frac{1}{2} \sqrt{\left(L^2+\Delta L^2+2 L \Delta L\right)-L^2}=\frac{1}{2} \sqrt{\left(\Delta L^2+2 L \Delta L\right)}
\end{aligned}
\)
As increase in length \(\Delta L\) is very small, therefore, neglecting \((\Delta L)^2\), we get
\(
x=\frac{\sqrt{2 L \Delta L}}{2} \dots(i)
\)
But \(\quad \Delta L=L \alpha \Delta t \dots(ii)\)
According to the problem, \(L=10 \mathrm{~m}\),
\(
\alpha=1.2 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}, \Delta T=20^{\circ} \mathrm{C}
\)
Substituting value of \(\Delta L\) in Eq. (i) from Eq. (ii)
\(
\begin{aligned}
x & =\frac{1}{2} \sqrt{2 L \times L \alpha \Delta t}=\frac{1}{2} L \sqrt{2 \alpha \Delta t} \\
& =\frac{10}{2} \times \sqrt{2 \times 1.2 \times 10^{-5} \times 20} \\
& =5 \times \sqrt{4 \times 1.2 \times 10^{-4}}=5 \times 2 \times 1.1 \times 10^{-2}=0.11 \mathrm{~m}=11 \mathrm{~cm}
\end{aligned}
\) -
Question 25 of 88
25. Question
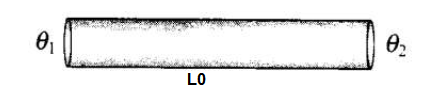
A thin rod having length \(L_0\) at \(0^{\circ} \mathrm{C}\) and coefficient of linear expansion \(\alpha\) has its two ends maintained at temperatures \(\theta_1\) and \(\theta_2\), respectlvely. Find its new length.
CorrectIncorrectHint
When temperature of a rod varies linearly, then average temperature of the middle point of the rod can be taken as mean of temperatures at the two ends. According to the diagram,
According to the diagram,
\(
\theta=\frac{\theta_1+\theta_2}{2}
\)
Let temperature varies linearly in the rod from its one end to other end from \(\theta_1\) to \(\theta_2\). Let \(\theta\) be the temperature of the mid-point of the rod. Therefore, average temperature of the mid-point of the rod is
\(
\Rightarrow \quad \theta=\frac{\theta_1+\theta_2}{2}
\)
Using relation, \(L=L_0(1+\alpha \theta)\)
or
\(
L=L_0\left[1+\alpha\left(\frac{\theta_1+\theta_2}{2}\right)\right]
\)
-
Question 26 of 88
26. Question
According to Stefan’s law of radiation, a black body radiates energy \(\sigma T^4\) from its unit surface area every second where \(T\) is the surface temperature of the black body and \(\sigma=5.67 \times 10^{-8} \mathrm{~W} /\) \(\mathrm{m}^2 \mathrm{~K}^4\) is known as Stefan’s constant. A nuclear weapon may be thought of as a ball of radius \(0.5 \mathrm{~m}\). When detonated, it reaches temperature of \(10^6 \mathrm{~K}\) and can be treated as a black body. Estimate the power it radiates.
CorrectIncorrectHint
\(
\begin{aligned}
& P=\sigma A T^4=\sigma\left(4 \pi R^2\right) \mathrm{T}^4 \\
& =5.67 \times 10^{-8} \times 4 \times 3.14 \times\left(0.5^{2} \times\left(10^6\right)^4\right. \\
& =1.78 \times 10^{17} \mathrm{~J} / \mathrm{s} \\
& \approx 1.8 \times 10^{17} \mathrm{~J} / \mathrm{s}
\end{aligned}
\) -
Question 27 of 88
27. Question
According to Stefan’s law of radiation, a black body radiates energy \(\sigma T^4\) from its unit surface area every second where \(T\) is the surface temperature of the black body and \(\sigma=5.67 \times 10^{-8} \mathrm{~W} /\) \(\mathrm{m}^2 \mathrm{~K}^4\) is known as Stefan’s constant. A nuclear weapon may be thought of as a ball of radius \(0.5 \mathrm{~m}\). When detonated, it reaches temperature of \(10^6 \mathrm{~K}\) and can be treated as a black body. If surrounding has water at \(30^{\circ} \mathrm{C}\), how much water can \(10 \%\) of the energy produced evaporate in \(1 \mathrm{~s}\) ?
\(
\left[S_w=4186.0 \mathrm{~J} / \mathrm{kg} \mathrm{K} \text { and } L_v=22.6 \times 10^5 \mathrm{~J} / \mathrm{kg}\right]
\)CorrectIncorrectHint
\(
\begin{aligned}
& P=\sigma A T^4=\sigma\left(4 \pi R^2\right) \mathrm{T}^4 \\
& =5.67 \times 10^{-8} \times 4 \times 3.14 \times\left(0.5^{2} \times\left(10^6\right)^4\right. \\
& =1.78 \times 10^{17} \mathrm{~J} / \mathrm{s} \\
& \approx 1.8 \times 10^{17} \mathrm{~J} / \mathrm{s}
\end{aligned}
\)The energy available per second,
\(
\begin{aligned}
& E=1.8 \times 10^{17} \mathrm{~J} / \mathrm{s} \\
\end{aligned}
\)
The energy required to evaporate water
\(
=10 \% \text { of } E=1.8 \times 10^{16} \mathrm{~J} / \mathrm{s}
\)
Energy used (per second) to raise temperature \(30^{\circ} \mathrm{C} \rightarrow 100^{\circ} \mathrm{C}\) and then into vapour at \(\left(100^{\circ} \mathrm{C}\right)\)
\(
\begin{aligned}
& =\mathrm{mS}_{\mathrm{w}} \Delta \theta+\mathrm{ml}_{\mathrm{v}} \\
& =\mathrm{m} \times 4186 \times(100-30)+\mathrm{m} \times 22.6 \times 10^5 \\
& =2.93 \times 10^5 \mathrm{~m}+22.6 \times 10^5 \mathrm{~m} \\
& =\mathrm{m}\left(25.53 \times 10^5 \mathrm{~J} / \mathrm{s}\right)
\end{aligned}
\)
From question, \(\mathrm{m}\left(25.53 \times 10^5\right)=1.8 \times 10^{16}\)
\(
\begin{aligned}
& \text { or } \mathrm{m}=\frac{1.8 \times 10^{16}}{25.53 \times 10^5} \\
& =7.0 \times 10^9 \mathrm{~kg}
\end{aligned}
\) -
Question 28 of 88
28. Question
According to Stefan’s law of radiation, a black body radiates energy \(\sigma T^4\) from its unit surface area every second where \(T\) is the surface temperature of the black body and \(\sigma=5.67 \times 10^{-8} \mathrm{~W} /\) \(\mathrm{m}^2 \mathrm{~K}^4\) is known as Stefan’s constant. A nuclear weapon may be thought of as a ball of radius \(0.5 \mathrm{~m}\). When detonated, it reaches temperature of \(10^6 \mathrm{~K}\) and can be treated as a black body. If surrounding has water at \(30^{\circ} \mathrm{C}\), how much water can \(10 \%\) of the energy produced evaporate in \(1 \mathrm{~s}\) ? If all this energy \(\mathrm{U}\) is in the form of radiation, corresponding momentum is \(p=U / c\). How much momentum per unit time does it impart on unit area at a distance of \(1 \mathrm{~km}\)?
CorrectIncorrectHint
\(
\begin{aligned}
& P=\sigma A T^4=\sigma\left(4 \pi R^2\right) \mathrm{T}^4 \\
& =5.67 \times 10^{-8} \times 4 \times 3.14 \times\left(0.5^{2} \times\left(10^6\right)^4\right. \\
& =1.78 \times 10^{17} \mathrm{~J} / \mathrm{s} \\
& \approx 1.8 \times 10^{17} \mathrm{~J} / \mathrm{s}
\end{aligned}
\)Momentum per unit time,
\(
\begin{aligned}
& \mathrm{P}=\frac{E}{c} \\
& =\frac{1.8 \times 10^{17}}{3 \times 10^8} \\
& =6 \times 10^9 \mathrm{~kg} .
\end{aligned}
\)
Momentum per unit time per unit area,
\(
\begin{aligned}
& P_1=\frac{P}{4 \pi R^2}=\frac{6 \times 10^8}{4 \times 3.14 \times\left(10^3\right)^2} \\
& P_1=47.7 \mathrm{~N} / \mathrm{m}^2
\end{aligned}
\) -
Question 29 of 88
29. Question
If two bodies are in thermal equilibrium in one frame, will they be in thermal equilibrium in all frames ?
CorrectIncorrectHint
If two bodies are in thermal equilibrium in one frame, they will be in thermal equilibrium in all the frames. In case there is any change in the temperature of one body due to change in frame, the same change will be acquired by the other body.
-
Question 30 of 88
30. Question
Does the temperature of a body depend on the frame from which it is observed?
CorrectIncorrectHint
No, the temperature of a body is not dependent on the frame from which it is observed. This is because atoms /molecules of matter move or vibrate in all possible directions. Increase in velocity at a particular direction of the container/ matter does not increase or decrease the overall velocity of the molecules/atoms because of the random collisions the entities suffer. So, there is no net rise in the temperature of the system.
-
Question 31 of 88
31. Question
In defining the ideal gas temperature scale, it is assumed that the pressure of the gas at constant volume is proportional to the temperature T . How can we verify whether this is true or not? Are we using the kinetic theory of gases?
CorrectIncorrectHint
The ideal gas thermometer is based on the ideal gas equation, \(P V=n R T\), where \(P\) is pressure of the gas at constant volume \(\mathrm{V}\) with \(\mathrm{n}\) number of moles at temperature \(\mathrm{T}\). Therefore, \(\mathrm{P}=\) constant \(\times \mathrm{T}\). According to this relation, if the volume of the gas used is constant, the pressure will be directly proportional to the temperature of the gas. We need not use the kinetic theory of gases or any experimental results.
-
Question 32 of 88
32. Question
Can the bulb of a thermometer be made of an adiabatic wall?
CorrectIncorrectHint
The bulb of a thermometer plays an important role in measuring the temperature of the surrounding body. It is put in contact with the body whose temperature is to be measured. The bulb attains the temperature of the body, which allows calibration of temperature. If the bulb is made of an adiabatic wall, then no heat will be transferred through the wall and the bulb cannot attain thermal equilibrium with the surrounding body. Therefore, the bulb cannot be made of an adiabatic wall.
-
Question 33 of 88
33. Question
If mercury and glass had equal coefficient of volume expansion, could we make a mercury thermometer in a glass tube?
CorrectIncorrectHint
Yes, we can make a mercury thermometer in a glass tube. Mercury and glass have equal coefficients of volume expansion. So, when temperature changes, the increase in the volume of the glass tube as which is equal to the real increase in volume minus the increase in the volume of the container, would be zero. Hence, it will give correct reading at every temperature.
-
Question 34 of 88
34. Question
The density of water at \(4^{\circ} \mathrm{C}\) is supposed to be \(1000 \mathrm{~kg} \mathrm{~m}^{-3}\). Is it same at the sea level and at a high altitude?
CorrectIncorrectHint
At sea level, the pressure is around 1 atmosphere and at high altitude, the density of air reduces.
Pressure of liquid,
\(
P=h \rho g \text {, }
\)
where \(\rho=\) density of fluid
The above equation shows that pressure depends on density. Therefore at \(4^{\circ} \mathrm{C}\), the density of water will be less at high altitude, compared to the density at sea level. -
Question 35 of 88
35. Question
A tightly closed metal lid of a glass bottle can be opened more easily if it is put in hot water for some time. Is it true?
CorrectIncorrectHint
When a bottle with a tightly-closed metal lid is put in hot water for sometime, its lid can be opened easily because metals have greater coefficient of expansion than glass. Therefore, when the metal lid comes in contact with hot water, it’ll expand more than the glass container. As a result, it will be easier to open the bottle.
-
Question 36 of 88
36. Question
If an automobile engine is overheated, it is cooled by putting water on it. It is advised that the water should be put slowly with the engine running. Is this true?
CorrectIncorrectHint
In a hot engine the hot parts are expanded because of heat, if cold water is poured suddenly then there will be uneven thermal contraction in the parts. This will result in a stress to develop between the various parts of the engine and may let the engine to crack down.
-
Question 37 of 88
37. Question
Is it possible for two bodies to be in thermal equilibrium if they are not in contact?
CorrectIncorrectHint
Two bodies are said to be in thermal equilibrium if they are at the same temperature. Consider two bodies A and B that are not in contact with each other but in contact with a heat reservoir. Since both the bodies will attain the temperature of the reservoir, they will be at the same temperature and, hence, in thermal equilibrium. Therefore, it is possible to have two bodies in thermal equilibrium even though they are not in contact.
-
Question 38 of 88
38. Question
A spherical shell is heated. The volume changes according to the equation \(V_\theta=V_0(1+\gamma \theta)\). Does the volume refer to the volume enclosed by the shell or the volume of the material making up the shell?
CorrectIncorrectHint
When a spherical shell is heated, its volume changes according to the equation, \(V_\theta=V_0(1+\gamma \Delta \theta)\). The volume referred to here is the volume of the material used to make up the shell, as its volume expands with the rise of temperature with coefficient of expansion of volume, \(\gamma\).
-
Question 39 of 88
39. Question
A system X is neither in thermal equilibrium with Y nor with Z. The systems Y and Z
CorrectIncorrectHint
The given data in the question is insufficient to specify the relation between the physical conditions of systems \(Y\) and \(Z\). As system \(X\) is not in thermal equilibrium with \(Y\) and \(Z\), systems \(Y\) and \(Z\) may be at the same temperature or they may or may not be in thermal equilibrium with each other. So, the only possible option is (c).
-
Question 40 of 88
40. Question
Which of the curves in the figure below represents the relation between Celsius and Fahrenheit temperatures?
 CorrectIncorrect
CorrectIncorrectHint
Celsius and Fahrenheit temperatures are related in the following way:
\(
C=\frac{5}{9} \mathrm{~F}-\frac{160}{9}
\)
Here, \(\mathrm{F}=\) temperature in Fahrenheit
\(C=\) temperature in Celsius
If this equation is plotted on the graph, then the curve will be represented by curve ‘a’ lying in the fourth quadrant with slope \(5 / 9\). -
Question 41 of 88
41. Question
Which of the following pairs may give equal numerical values of the temperature of a body?
CorrectIncorrectHint
If we consider \(T_F\) and \(T_K\) as the temperatures measured in Fahrenheit and Kelvin scales respectively, then \(T_F=T_K=\theta=574.59^{\circ}\) where, \(\theta\) is the temperature in Fahrenheit and Kelvin scales. But in case of Celsius and Kelvin scales, such \(\theta\) does not exist.
Also, in Kelvin and Platinum scales, they depend on the properties of the thermometric substance used to define the scale. Hence, such value does not exist in Kelvin and Platinum.Let \(\theta\) be the temperature in Fahrenheit and Kelvin scales.
We know that the relation between the temperature in Fahrenheit and Kelvin scales is given by
\(
\begin{aligned}
& \frac{T_F-32}{180}=\frac{T_K-273.15}{100} \\
& T_F=T_K=\theta
\end{aligned}
\)
Therefore,
\(
\begin{aligned}
& \frac{\theta-32}{180}=\frac{\theta-273.15}{100} \\
& 5 \theta-160=9 \theta-2458.5 \\
& 4 \theta=2298.35 \\
& \theta=574.59^{\circ}
\end{aligned}
\) -
Question 42 of 88
42. Question
For a constant volume gas thermometer, one should fill the gas at
CorrectIncorrectHint
A constant-volume gas thermometer should be filled with an ideal gas in which particles don’t interact with each other and are free to move anywhere so that the thermometer functions properly. An ideal gas is only a theoretical possibility. Therefore, the gas that is filled in the thermometer should be at high temperature and low pressure, as under these conditions, a gas behaves as an ideal gas.
-
Question 43 of 88
43. Question
Consider the following statements:
(A) The coefficient of linear expansion has dimension \(K^{-1}\).
(B) The coefficient of volume expansion has dimension \(K^{-1}\).CorrectIncorrectHint
The coefficient of linear expansion,
\(
\begin{aligned}
& \propto=\frac{1}{L} \frac{\Delta L}{\Delta T} \\
& =\frac{|L|}{|L T|}=K^{-1}
\end{aligned}
\)
Here, \(L=\) initial length
\(\Delta \mathrm{L}=\) change in length
\(\Delta T=\) change in temperature
On the other hand, the coefficient of volume expansion,
\(
\gamma=\frac{1}{V} \frac{\Delta V}{\Delta T}=\frac{\left|L^3\right|}{\left|L^3 T\right|}=K^{-1}
\)
Here, V = initial volume
\(\Delta \mathrm{V}=\) change in volume
\(\Delta \mathrm{T}=\) change in temperature
\(K=\) kelvin, the S.I. unit of temperature -
Question 44 of 88
44. Question
A metal sheet with a circular hole is heated. The hole
CorrectIncorrectHint
When a metal sheet is heated, it starts expanding and its surface area will start increasing, which will lead to an increase in the radius of the hole. Hence, the circular hole will become larger.
-
Question 45 of 88
45. Question
Two identical rectangular strips, one of copper and the other of steel, are rivetted together to form a bimetallic strip \(\left(\alpha_{\text {copper }}>\alpha_{\text {steel }}\right)\). On heating, this strip will
CorrectIncorrectHint
bend with copper on convex side
We are provided with two metal strips of copper and steel. On heating, both of them will expand. Expansion coefficient of copper is more than that of steel. So, the copper metal strip will expand more, causing the bimetallic strip to bend with copper at the convex side, as it’ll have more surface area compared to the steel sheet, which will be on the concave side. -
Question 46 of 88
46. Question
If the temperature of a uniform rod is slightly increased by \(\Delta t\), its moment of inertia \(I\) about a perpendicular bisector increases by
CorrectIncorrectHint
The change in moment of inertia of uniform rod with change in temperature is given by, \(I^{\prime}=I(1+2 \propto \Delta t)\)
Here, \(I\) = initial moment of inertia
\(\mathrm{I}^{\prime}=\) new moment of inertia due to change in temperature
\(\alpha=\) expansion coefficient
\(\Delta \mathrm{t}=\) change in temperature
So, \(I^{\prime}-I=2 \alpha I \Delta t\) -
Question 47 of 88
47. Question
If the temperature of a uniform rod is slightly increased by \(\Delta t\), its moment of inertia \(I\) about a line parallel to itself will increase by
CorrectIncorrectHint
The change in moment of inertia of uniform rod with change in temperature is given by, \(I^{\prime}=I(1+2 \propto \Delta t)\)
Here, \(I\) = initial moment of inertia
\(\mathrm{I}^{\prime}=\) new moment of inertia due to change in temperature
\(\alpha=\) expansion coefficient
\(\Delta \mathrm{t}=\) change in temperature
So, \(I^{\prime}-I=2 \alpha I \Delta t\) -
Question 48 of 88
48. Question
The temperature of water at the surface of a deep lake is \(2^{\circ} \mathrm{C}\). The temperature expected at the bottom is
CorrectIncorrectHint
The density of water is maximum at \(4^{\circ} \mathrm{C}\), and the water at the bottom of the lake is most dense, compared to the layers of water above. Therefore, the temperature expected at the bottom is \(4^{\circ} \mathrm{C}\).
-
Question 49 of 88
49. Question
An aluminium sphere is dipped into water at \(10^{\circ} \mathrm{C}\). If the temperature is increased, the force of buoyancy
CorrectIncorrectHint
will decrease
When an aluminium sphere is dipped in water and the temperature of water is increased, the aluminium will start expanding leading to increase in its volume. This will lead to increase in the surface area of the shell and it’ll exert less pressure on the water such that the volume of the sphere submerged in water will decrease and it’ll start float easily on water. Now, the volume of water displaced will be less compared to what was displaced initially. Therefore, the force of buoyancy will decrease, as it is directly proportional to the volume of water displaced. -
Question 50 of 88
50. Question
A spinning wheel is brought in contact with an identical wheel spinning at identical speed. The wheels slow down under the action of friction. Which of the following energies of the first wheel decrease?
CorrectIncorrectHint
(a) Kinetic
(c) Mechanical
The kinetic energy of a body depends on its speed. Since when a spinning wheel is slowed down, its speed decreases leading to reduction in its kinetic energy. The mechanical energy of a body is defined as the sum of its potential and kinetic energies. Since the kinetic energy of the wheel has been decreased, it’ll lead to decrease in its mechanical energy. When the wheel slows down due to friction, its mechanical energy gets converted into heat energy, leading to increase in internal energy, which increases with increase in temperature. -
Question 51 of 88
51. Question
A spinning wheel A is brought in contact with another wheel B initially at rest. Because of the friction at contact, the second wheel also starts spinning. Which of the following energies of the wheel B increase?
CorrectIncorrectHint
(a) Kinetic
(b) Total
(c) Mechanical
(d) Internal
When the wheel B starts spinning because of the friction at contact, it will gain kinetic energy and, hence, mechanical energy (kinetic + potential energies). Also, internal energy will increase, which increases with rise in temperature. Along with it, the generation of heat energy due to friction will lead to increase in the net sum of all the energies, i.e. total energy. -
Question 52 of 88
52. Question
A body A is placed on a railway platform and an identical body B in a moving train. Which of the following energies of B are greater than those of A as seen from the ground?
CorrectIncorrectHint
(a) Kinetic
(b) Total
(c) Mechanical
As body A is at rest on the ground, it possesses only potential energy, whereas body B, being placed inside a moving train, possesses kinetic energy due to its motion along with the train. Therefore, body B will have greater kinetic, mechanical (energy possessed by the body by virtue of its position and motion = kinetic energy+potential energy) energy and, hence, total (sum of all the energies) energy. No information is given about the temperature of the body so we can not say whether body B’s internal energy will be or will not be greater than that of body A. -
Question 53 of 88
53. Question
In which of the following pairs of temperature scales, the size of a degree is identical?
CorrectIncorrectHint
(c) Celsius scale and ideal gas scale
(d) Ideal gas scale and absolute scale
Celsius scale and ideal gas scale measure temperature in kelvin (K) and the ideal gas scale is sometimes also called the absolute scale. A mercury scale gives reading in degrees and its size of degree, which depends on length of mercury column, doesn’t match any of the above-mentioned scales. -
Question 54 of 88
54. Question
A solid object is placed in water contained in an adiabatic container for some time. The temperature of water falls during the period and there is no appreciable change in the shape of the object. The temperature of the solid object
CorrectIncorrectHint
must have increased.
The whole system (water + solid object) is enclosed in an adiabatic container from which no heat can escape. After some time, the temperature of water falls, which implies that the heat from the water has been transferred to the object, leading to increase in its temperature. -
Question 55 of 88
55. Question
As the temperature is increased, the time period of a pendulum
CorrectIncorrectHint
In general, the time period of a pendulum, \(t\), is given by
\(
\mathrm{t}=\frac{1}{2 \pi} \sqrt{\frac{1}{g}}
\)
When the temperature \((T)\) is increased, the length of the pendulum \((l)\) is given by,
\(
l=l_0(1+\alpha \mathrm{T}) \text {, }
\)
where \(l_0=\) length at \(0^{\circ} \mathrm{C}\)
\(\alpha=\) linear coefficient of expansion.
Therefore, the time period of a pendulum will be
\(
\mathrm{t}=\frac{1}{2 \pi} \sqrt{\frac{l_0(1+\propto T)}{g}}
\)
Hence, time period of a pendulum will increase with increase in temperature. -
Question 56 of 88
56. Question
The steam point and the ice point of a mercury thermometer are marked as \(80^{\circ}\) and \(20^{\circ}\). What will be the temperature in centigrade mercury scale when this thermometer reads \(32^{\circ}\)?
CorrectIncorrectHint
Given:
Ice point of a mercury thermometer, \(T_0=20^{\circ} \mathrm{C}\)
Steam point of a mercury thermometer, \(T_{100}=80^{\circ} \mathrm{C}\)
Temperature on thermometer that is to be calculated in centigrade scale, \(T_1=32^{\circ} \mathrm{C}\)
Temperature on a centigrade mercury scale, \(\mathrm{T}\), is given as:
\(
\begin{aligned}
& \mathrm{T}=\frac{T_1-T_0}{T_{100}-T_0} \times 100 \\
& \Rightarrow T=\frac{32-20}{80-20} \times 100 \\
& \Rightarrow T=\frac{12}{60} \times 100 \\
& \Rightarrow T=\frac{120}{6} \\
& \Rightarrow \mathrm{T}=20^{\circ} \mathrm{C}
\end{aligned}
\)
Therefore, the temperature on a centigrade mercury scale will be \(20^{\circ} \mathrm{C}\). -
Question 57 of 88
57. Question
A constant volume thermometer registers a pressure of \(1.500 \times 10^4 \mathrm{~Pa}\) at the triple point of water and a pressure of \(2.050 \times 10^4 \mathrm{~Pa}\) at the normal boiling point. What is the temperature at the normal boiling point?
CorrectIncorrectHint
Given:
Pressure registered by a constant-volume thermometer at the triple point, \(\mathrm{P}_{\mathrm{tr}}=1.500 \times 10^4 \mathrm{~Pa}\)
Pressure registered by the thermometer at the normal boiling point, \(P=2.050 \times 10^4 \mathrm{~Pa}\)
We know that for a constant-volume gas thermometer, temperature \((T)\) at the normal boiling point is given as:
\(
\begin{aligned}
& \mathrm{T}=\frac{P}{P_{t r}} \times 273.16 \mathrm{~K} \\
& \Rightarrow T=\frac{2.050 \times 10^4}{1.500} \times 10^4 \times 273.16 \mathrm{~K} \\
& \Rightarrow \mathrm{T}=373.31 \mathrm{~K}
\end{aligned}
\)
Therefore, the temperature at the normal point \((\mathrm{T})\) is \(373.31 \mathrm{~K}\). -
Question 58 of 88
58. Question
A gas thermometer measures the temperature from the variation of pressure of a sample of gas. If the pressure measured at the melting point of lead is 2.20 times the pressure measured at the triple point of water, find the melting point of lead.
CorrectIncorrectHint
Given:
In a gas thermometer, the pressure measured at the melting point of lead, \(P=2.20 \times\) Pressure at triple point \(\left(P_{t r}\right)\)
So the melting point of lead, \((T)\) is given as:
\(
\begin{aligned}
& T=\frac{P}{P_{t r}} \times 273.16 \mathrm{~K} \\
& \Rightarrow T=\frac{2.20 \times P_{t r}}{P_{t r}} \times 273.16 \mathrm{~K} \\
& \Rightarrow \mathrm{T}=2.20 \times 273.16 \mathrm{~K} \\
& \Rightarrow \mathrm{T}=600.952 \mathrm{~K} \\
& \Rightarrow \mathrm{T} \cong 601 \mathrm{~K}
\end{aligned}
\)
Therefore, the melting point of lead is \(601 \mathrm{~K}\). -
Question 59 of 88
59. Question
The pressure measured by a constant volume gas thermometer is \(40 \mathrm{kPa}\) at the triple point of water. What will be the pressure measured at the boiling point of water \(\left(100^{\circ} \mathrm{C}\right)\)?
CorrectIncorrectHint
Given:
Pressure measured by a constant volume gas thermometer at the triple point of water, \(P_{t r}=40 \mathrm{kPa}=40 \times\) \(10^3 \mathrm{~Pa}\)
Boiling point of water, \(T=100^{\circ} \mathrm{C}=373.16 \mathrm{~K}\)
Let the pressure measured at the boiling point of water be \(P\).
For a constant volume gas thermometer, temperature-pressure relation is given below:
\(
\begin{aligned}
& T=\frac{P}{P_{t r}} \times 273.16 K \\
& \Rightarrow P=\frac{T \times P_{t r}}{273.16} \\
& \Rightarrow P=\frac{373.16 \times 40 \times 10^3}{273.16} \\
& \Rightarrow P=54643 P a \\
& \Rightarrow P=54.6 \times 10^3 \mathrm{~Pa} \\
& \Rightarrow P \simeq 55 \mathrm{kPa}
\end{aligned}
\)
Therefore, the pressure measured at the boiling point of water is \(55 \mathrm{kPa}\). -
Question 60 of 88
60. Question
The pressure of the gas in a constant volume gas thermometer is \(70 \mathrm{kPa}\) at the ice point. Find the pressure at the steam point.
CorrectIncorrectHint
Given:
Temperature of ice point, \(T_1=273.15 \mathrm{~K}\)
Temperature of steam point, \(T_2=373.15 \mathrm{~K}\)
Pressure of the gas in a constant volume thermometer at the ice point, \(P_1=70 \mathrm{kPa}\),
Let \(P_{t r}\) be the pressure at the triple point and \(P_2\) be the pressure at the steam point.
The temperature-pressure relations for ice point and steam point are given below:
For ice point,
\(
\begin{aligned}
& T_1=\frac{P_1}{P_{t r}} \times 273.16 K \\
& \Rightarrow 273.15=\frac{70}{P_{t r}} \times 10^3 \times 273.16 \\
& \Rightarrow P_{t r}=\frac{70 \times 273.16 \times 10^3}{273.15} P a
\end{aligned}
\)
For steam point,
\(
T_2=\frac{P_2 \times 273.16}{P_{t r}} K
\)
On substituting the value of \(P_{\text {tr }}\), we get:
\(
\begin{aligned}
& 373.15=\frac{P_2 \times 273.15 \times 273.16}{70 \times 273.16 \times 10^3} \\
& \Rightarrow P_2=\frac{373.15 \times 70 \times 10^3}{273.15} \\
& \Rightarrow P_2=95.626 \times 10^3 \mathrm{~Pa} \\
& \Rightarrow P_2 \simeq 96 \mathrm{kPa}
\end{aligned}
\)
Therefore, the pressure at steam point is \(96 \mathrm{kPa}\). -
Question 61 of 88
61. Question
The pressures of the gas in a constant volume gas thermometer are 80 cm, 90 cm and 100 cm of mercury at the ice point, the steam point, and in a heated wax bath respectively. Find the temperature of the wax bath.
CorrectIncorrectHint
Given:
In a constant-volume gas thermometer,
Pressure of the gas at the ice point, \(P_0=80 \mathrm{~cm}\) of \(\mathrm{Hg}\)
Pressure of the gas at the steam point, \(P_{100}=90 \mathrm{~cm}\) of \(\mathrm{Hg}\)
Pressure of the gas in a heated wax bath, \(P=100 \mathrm{~cm}\) of \(\mathrm{Hg}\)
The temperature of the wax bath
\((T)\) is given by:
\(
\begin{aligned}
& T=\frac{P-P_0}{P_{100}-P_0} \times 100^{\circ} \mathrm{C} \\
& \Rightarrow T=\frac{100-80}{90-80} \times 100 \\
& \Rightarrow T=\frac{20}{10} \times 100 \\
& \Rightarrow T=200^{\circ} C
\end{aligned}
\)
Therefore, the temperature of the wax bath is \(200^{\circ} \mathrm{C}\). -
Question 62 of 88
62. Question
In a Callender’s compensated constant pressure air thermometer, the volume of the bulb is 1800 cc. When the bulb is kept immersed in a vessel, 200 cc of mercury has to be poured out. Calculate the temperature of the vessel.
CorrectIncorrectHint
Given:
Volume of the bulb in a Callender’s compensated constant pressure air thermometer, \((\mathrm{V})=\) \(1800 \mathrm{cc}\)
Volume of mercury that has to be poured out, \(V^{\prime}=200 \mathrm{cc}\)
Temperature of ice bath, \(T_0=273.15 \mathrm{~K}\)
So the temperature of the vessel \(\left(T^{\prime}\right)\) is given by:
\(
\begin{aligned}
& T^{\prime}=\frac{V}{V-V^{\prime}} \times T_0 \\
& \Rightarrow T^{\prime}=\frac{1800}{1600} \times 273.15 K \\
& \Rightarrow T^{\prime}=307.293 \\
& \Rightarrow T^{\prime} \simeq 307 K
\end{aligned}
\)
Therefore, the temperature of the vessel is \(307 \mathrm{~K}\). -
Question 63 of 88
63. Question
A platinum resistance thermometer reads \(0^{\circ}\) when its resistance is \(80 \Omega\) and \(100^{\circ}\) when its resistance is \(90 \Omega\). Find the temperature at the platinum scale at which the resistance is \(86 \Omega\).
CorrectIncorrectHint
Given:
\(
\text { Resistance at } 0^{\circ} \mathrm{C}, R_0=80 \Omega
\)
Resistance at \(100^{\circ} \mathrm{C}, R_{100}=90 \Omega\)
Let \(t\) be the temperature at which the resistance \(\left(R_t\right)\) is 86 \(\Omega\)
\(
\begin{aligned}
& t=\frac{R_t-R_0}{R_{100}-R_0} \times 100 \\
& \Rightarrow t=\frac{86-80}{90-80} \times 100 \\
& \Rightarrow t=\frac{6}{10} \times 100 \\
& \Rightarrow t=60^{\circ}
\end{aligned}
\)
Therefore, the resistance is 86 \(\Omega\) at \(60^{\circ} \mathrm{C}\) -
Question 64 of 88
64. Question
A resistance thermometer reads \(R=20.0 \Omega, 27.5 \Omega\), and \(50.0 \Omega\) at the ice point \(\left(0^{\circ} \mathrm{C}\right)\), the steam point \(\left(100^{\circ} \mathrm{C}\right)\) and the zinc point \(\left(420^{\circ} \mathrm{C}\right)\) respectively. Assuming that the resistance varies with temperature as \(R_\theta=R_0\left(1+\alpha \theta+\beta \theta^2\right)\), find the values of \(R_0, \alpha\) and \(\beta\). Here \(\theta\) represents the temperature on Celsius scale.
CorrectIncorrectHint
Given:
Reading on resistance thermometer at ice point, \(R_0=20 \Omega\)
Reading on resistance thermometer at steam point, \(R_{100}=27.5 \Omega\)
Reading on resistance thermometer at zinc point, \(R_{420}=50 \Omega\)
The variation of resistance with temperature in Celsius scale, \(\theta\), is given as:
\(
\begin{aligned}
& R_{100}=R_0\left(1+\alpha \theta+\beta \theta^2\right) \\
& \Rightarrow R_{100}=R_0+R_0 \alpha \theta+R_0 \beta \theta^2 \\
& \Rightarrow R_{100}=R_0+R_0 \alpha \theta+R_0 \beta \theta^2 \\
& \Rightarrow \frac{\left(R_{100}-R_0\right)}{R_0}=\alpha \theta+\beta \theta^2 \\
& \Rightarrow \frac{27.5-20}{20}=\alpha \theta+\beta \theta^2 \\
& \Rightarrow \frac{7.5}{20}=\alpha \times 100+\beta \times 10000 \ldots(i)
\end{aligned}
\)
\(
\begin{aligned}
& \text { Also, } R_{420}=R_0\left(1+\alpha \theta+\beta \theta^2\right) \\
& \Rightarrow R_{420}=R_0+R_0 \alpha \theta+R_0 \beta \theta^2 \\
& \Rightarrow \frac{R_{420}-R_0}{R_0}=\alpha \theta+\beta \theta^2 \\
& \Rightarrow \frac{50-20}{20}=420 \alpha+176400 \beta \\
& \Rightarrow \frac{3}{2}=420 \alpha+176400 \beta \ldots(i i)
\end{aligned}
\)
Solving (i) and (ii), we get:
\(
\begin{aligned}
& \alpha=3.8 \times 10^{-3 \circ} \mathrm{C}^{-1} \\
& \beta=-5.6 \times 10^{-7 \circ} \mathrm{C}^{-1}
\end{aligned}
\)
Therefore, resistance \(R_0\) is \(20 \Omega\) and the value of \(\alpha\) is \(3.8 \times 10^{-3 \circ} \mathrm{C}^{-1}\) and that of \(\beta\) is \(-5.6 \times 10^{-7 \circ} \mathrm{C}^{-2}\). -
Question 65 of 88
65. Question
A concrete slab has a length of \(10 \mathrm{~m}\) on a winter night when the temperature is \(0^{\circ} \mathrm{C}\). Find the length of the slab on a summer day when the temperature is \(35^{\circ} \mathrm{C}\). The coefficient of linear expansion of concrete is \(1.0 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}\)
CorrectIncorrectHint
Given:
Length of the slab when the temperature is \(0^{\circ} \mathrm{C}, L_0=10 \mathrm{~m}\)
Temperature on the summer day, \(t=35^{\circ} \mathrm{C}\)
Let \(L_1\) be the length of the slab on a summer day when the temperature is \(35^{\circ} \mathrm{C}\).
The coefficient of linear expansion of concrete, \(\alpha=1 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}\)
\(
\begin{aligned}
& L_1=L_0(1+\propto t) \\
& \Rightarrow L_1=10\left(1+10^{-5} \times 35\right) \\
& \Rightarrow L_1=10+35 \times 10^{-4} \\
& \Rightarrow L_1=10.0035 \mathrm{~m}
\end{aligned}
\)
So, the length of the slab on summer day when the temperature is \(35^{\circ} \mathrm{C}\) is \(10.0035 \mathrm{~m}\). -
Question 66 of 88
66. Question
A metre scale made of steel is calibrated at \(20^{\circ} \mathrm{C}\) to give correct reading. Find the distance between \(50 \mathrm{~cm}\) mark and \(51 \mathrm{~cm}\) mark if the scale is used at \(10^{\circ} \mathrm{C}\). Coefficient of linear expansion of steel is \(1.1 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}\).
CorrectIncorrectHint
Given:
Temperature at which the steel metre scale is calibrated, \(t_1=20^{\circ} \mathrm{C}\)
Temperature at which the scale is used, \(\mathrm{t}_2=10^{\circ} \mathrm{C}\)
So, the change in temperature,
\(
\begin{aligned}
& \Delta \mathrm{t}=(20^{\circ} & \left.-10^{\circ}\right) \mathrm{C} \\
\end{aligned}
\)
The distance to be measured by the metre scale, \(L_0=51\)
\(
-50)=1 \mathrm{~cm}=0.01 \mathrm{~m}
\)
Coefficient of linear expansion of steel,
\(
\alpha_{\text {steel }}=1.1 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}
\)
Let the new length measured by the scale due to expansion of steel be \(L_2\), Change in length is given by,
\(
\begin{aligned}
& \Delta \mathrm{L}=\mathrm{L}_1 \propto_{\text {steel }} \Delta \mathrm{t} \\
& \Rightarrow \Delta L=1 \times 1.1 \times 10^{-5} \times 10 \\
& \Rightarrow \Delta L=0.00011 \mathrm{~cm}
\end{aligned}
\)
As the temperature is decreasing, therefore length will decrease by
\(\Delta L\)
Therefore, the new length measured by the scale due to expansion of steel \(\left(L_2\right)\) will be,
\(
\mathrm{L}_2=1 \mathrm{~cm}
\)
\(-0.00011 \mathrm{~cm}=0.99989 \mathrm{~cm}\) -
Question 67 of 88
67. Question
railway track (made of iron) is laid in winter when the average temperature is \(18^{\circ} \mathrm{C}\). The track consists of sections of \(12.0 \mathrm{~m}\) placed one after the other. How much gap should be left between two such sections so that there is no compression during summer when the maximum temperature goes to \(48^{\circ} \mathrm{C}\)? Coefficient of linear expansion of iron \(=11 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\).
CorrectIncorrectHint
Given, Length of the iron sections when there’s no effect of temperature on them, \(L_0=12.0 \mathrm{~m}\)
Temperature at which the iron track is laid in winter, \(t_w=18^{\circ} \mathrm{C}\)
Maximum temperature during summers, \(\mathrm{t}_{\mathrm{s}}=48^{\circ} \mathrm{C}\)
Coefficient of linear expansion of iron,
\(
\alpha=11 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}
\)
Let the new lengths attained by each section due to expansion of iron in winter and summer be \(L_w\) and \(L_s\), respectively, which can be calculated as follows:
\(
\begin{aligned}
& L_w=L_0\left(1+\alpha t_w\right) \\
& \Rightarrow L_w=12\left(1+11 \times 10^{-6} \times 18\right) \\
& \Rightarrow L_w=12.00237 \mathrm{~m} \\
& L_s=L_0\left(1+\alpha t_s\right) \\
& \Rightarrow L_s=12\left(1+11 \times 10^{-6} \times 48\right) \\
& \Rightarrow L_s=12.006336 \mathrm{~m} \\
& \therefore \Delta L=L_s-L_w \\
& \Rightarrow \Delta L=12.006336-12.002376 \\
& \Rightarrow \Delta L=0.00396 \mathrm{~m} \\
& \Rightarrow \Delta L \approx 0.4 \mathrm{~cm}
\end{aligned}
\)
Therefore, the gap \((\Delta L)\) that should be left between two iron sections, so that there is no compression during summer, is \(0.4 \mathrm{~cm}\). -
Question 68 of 88
68. Question
A circular hole of diameter \(2.00 \mathrm{~cm}\) is made in an aluminium plate at \(0^{\circ} \mathrm{C}\). What will be the diameter at \(100^{\circ} \mathrm{C} ? \alpha\) for aluminium \(=2.3 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}\).
CorrectIncorrectHint
Given:
Diameter of a circular hole in an aluminium plate at \(0^{\circ} \mathrm{C}, \mathrm{d}_1=2 \mathrm{~cm}=2 \times 10^{-2} \mathrm{~m}\) Initial temperature, \(\mathrm{t}_1=0^{\circ} \mathrm{C}\)
Final temperature, \(t_2=100^{\circ} \mathrm{C}\)
So, the change in temperature, \((\Delta t)=100^{\circ} \mathrm{C}-0^{\circ} \mathrm{C}=100^{\circ} \mathrm{C}\)
The linear expansion coefficient of aluminium, \(\alpha_{a l}=2.3 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}\)
Let the diameter of the circular hole in the plate at \(100^{\circ} \mathrm{C}\) be \(\mathrm{d}_2\), which can be written as
\(
\begin{aligned}
& d_2=d_1(1+\alpha \Delta t) \\
& \Rightarrow d_2=2 \times 10^{-2}\left(1+2.3 \times 10^{-5} \times 10^2\right) \\
& \Rightarrow d_2=2 \times 10^{-2}\left(1+2.3 \times 10^{-3}\right) \\
& \Rightarrow d_2=2 \times 10^{-2}+2.3 \times 2 \times 10^{-5} \\
& \Rightarrow d^2=0.02+0.000046 \\
& \Rightarrow d^2=0.020046 \mathrm{~m} \\
& \Rightarrow d^2 \approx 2.0046 \mathrm{~cm}
\end{aligned}
\)
Therefore, the diameter of the circular hole in the aluminium plate at \(100^{\circ} \mathrm{C}\) is \(2.0046 \mathrm{~cm}\). -
Question 69 of 88
69. Question
Two metre scales, one of steel and the other of aluminium, agree at \(20^{\circ} \mathrm{C}\). Calculate the ratio aluminium-centimetre/steel-centimetre at (a) \(0^{\circ} \mathrm{C}\), (b) \(40^{\circ} \mathrm{C}\) and (c) \(100^{\circ} \mathrm{C}\). \(\alpha\) for steel \(=1.1 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}\) and for aluminium \(=2.3 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}\).
CorrectIncorrectHint
Given:
At \(20^{\circ} \mathrm{C}\), length of the metre scale made up of steel, \(L_{s t}=\) length of the metre scale made up of aluminium, \(L_{\text {al }}\) Coefficient of linear expansion for aluminium, \(\alpha_{a l}=2.3 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}\)
Coefficient of linear expansion for steel, \(\alpha_{\text {st }}=1.1 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}\)
Let the length of the aluminium scale at \(0^{\circ} \mathrm{C}, 40^{\circ} \mathrm{C}\) and \(100^{\circ} \mathrm{C}\) be \(L_{\text {0al }}, L_{40 \text { al }}\) and \(L_{100 a l}\).
And let the length of the steel scale at \(0^{\circ} \mathrm{C}, 40^{\circ} \mathrm{C}\) and \(100^{\circ} \mathrm{C}\) be \(L_{0 s t}, L_{40 \text { st }}\) and \(L_{100 s t}\).
(a) So, \(L_{0 s t}\left(1-\alpha_{\text {st }} \times 20\right)=L_{0 a l}\left(1-\alpha_{a l} \times 20\right)\)
\(
\begin{aligned}
& \frac{L_{0 s t}}{L_{0 a l}}=\frac{\left(1-\alpha_{a l} \times 20\right)}{\left(1-\alpha_{s t} \times 20\right)} \\
& \Rightarrow \frac{L_{0 s t}}{L_{0 a l}}=\frac{1-2.3 \times 10^{-5} \times 20}{1-1.1 \times 10^{-5} \times 20} \\
& \Rightarrow \frac{L_{0 s t}}{L_{0 a l}}=\frac{0.99954}{0.99978} \\
& \Rightarrow \frac{L_{0 s t}}{L_{0 a l}}=0.999759
\end{aligned}
\)
\(
\begin{aligned}
& \text { (b) } \frac{L_{40 a l}}{L_{40 s t}}=\frac{L_{0 a l}\left(1+\alpha_{a l} \times 40\right)}{L_{0 s t}\left(1+\alpha_{s t} \times 40\right)} \\
& \Rightarrow \frac{L_{40 a l}}{L_{40 s t}}=\frac{L_{0 a l}}{L_{0 s t}} \times \frac{\left(1+2.3 \times 10^{-5} \times 40\right)}{\left(1+1.1 \times 10^{-5} \times 40\right)} \\
& \Rightarrow \frac{L_{40 a l}}{L_{40 s t}}=\frac{0.99977 \times 1.00092}{1.00044} \\
& \Rightarrow \frac{L_{40 a l}}{L_{40 s t}}=1.0002496 \\
& \text { (c) } \frac{L_{100 a l}}{L_{100 s t}}=\frac{L_{0 a l}\left(1+\alpha_{a l} \times 100\right)}{L_{0 s t}\left(1+\alpha_{s t} \times 100\right)} \\
& \Rightarrow \frac{L_{100 a l}}{L_{100 s t}}=\frac{0.99977 \times 1.0023}{1.0023} \\
& \Rightarrow \frac{L_{100 a l}}{L_{100 s t}}=1.00096
\end{aligned}
\) -
Question 70 of 88
70. Question
A metre scale is made up of steel and measures correct length at \(16^{\circ} \mathrm{C}\). What will be the percentage error if this scale is used (a) on a summer day when the temperature is \(46^{\circ} \mathrm{C}\) and (b) on a winter day when the temperature is \(6^{\circ} \mathrm{C}\)? Coefficient of linear expansion of steel \(=11 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\)
CorrectIncorrectHint
The change in length is given as,
\(
\begin{aligned}
& \Delta \mathrm{L}=\mathrm{L} \alpha \Delta \mathrm{T} \\
& \frac{\Delta \mathrm{L}}{\mathrm{L}}=11 \times 10^{-6} \times -30
\end{aligned}
\)
The error percentage is given as,
\(
\begin{aligned}
& \% \mathrm{e}=\left(\frac{\Delta \mathrm{L}}{\mathrm{L}} \times 100\right) \% \\
& \% \mathrm{e}=\left(11 \times 10^{-6} \times -30 \times 100\right) \% \\
& =-3.3 \times 10^{-2} \%
\end{aligned}
\)
(b)
The change in length is given as,
\(
\begin{aligned}
& \Delta \mathrm{L}=\mathrm{L} \alpha \Delta \mathrm{T} \\
& \frac{\Delta \mathrm{L}}{\mathrm{L}}=11 \times 10^{-6} \times 10
\end{aligned}
\)
The error percentage is given as,
\(
\begin{aligned}
& \% \mathrm{e}=\left(\frac{\Delta \mathrm{L}}{\mathrm{L}} \times 100\right) \% \\
& \% \mathrm{e}=\left(11 \times 10^{-6} \times 10 \times 100\right) \% \\
& =1.1 \times 10^{-2} \%
\end{aligned}
\)
Thus, the error percentages are \(-3.3 \times 10^{-2} \%\) and \(1.1 \times 10^{-2} \%\). -
Question 71 of 88
71. Question
A metre scale made of steel reads accurately at \(20^{\circ} \mathrm{C}\). In a sensitive experiment, distances accurate up to \(0.055 \mathrm{~mm}\) in \(1 \mathrm{~m}\) are required. Find the range of temperature in which the experiment can be performed with this metre scale. Coefficient of linear expansion of steel \(=11 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\)
CorrectIncorrectHint
Given:
Temperature at which a metre scale gives an accurate reading, \(T_1=20^{\circ} \mathrm{C}\)
The value of variation admissible, \(\Delta \mathrm{L}=0.055 \mathrm{~mm}=0.055 \times 10^{-3} \mathrm{~m}\), in the length, \(\mathrm{L}_0=1 \mathrm{~m}\)
Coefficient of linear expansion of steel, \(\alpha=11 \times 10^{-6} \mathrm{C}^{-1}\)
Let the range of temperature in which the experiment can be performed be \(T_2\).
We know: \(\Delta \mathrm{L}=\mathrm{L}_0 \alpha \Delta \mathrm{T}\)
\(
\begin{aligned}
& \Rightarrow 0.055 \times 10^{-3}=1 \times 11 \times 10^{-6} \times\left(T_1 \pm T_2\right) \\
& \Rightarrow 5 \times 10^{-3}=\left(20 \pm T_2\right) \times 10^{-3} \\
& \Rightarrow 20 \pm T_2=5 \\
& \text { Either } T_2=20+5=25^{\circ} \mathrm{C} \\
& \text { or } T_2=20-5=15^{\circ} \mathrm{C}
\end{aligned}
\)
Hence, the experiment can be performed in the temperature range of \(15^{\circ} \mathrm{C}\) to \(25^{\circ} \mathrm{C}\) -
Question 72 of 88
72. Question
The density of water at \(0^{\circ} \mathrm{C}\) is \(0.998 \mathrm{~g} \mathrm{~cm}^{-3}\) and at \(4^{\circ} \mathrm{C}\) is \(1.000 \mathrm{~g} \mathrm{~cm}^{-3}\). Calculate the average coefficient of volume expansion of water in the temperature range 0 to \(4^{\circ} \mathrm{C}\).
CorrectIncorrectHint
Given:
Density of water at \(0^{\circ} \mathrm{C},\left(f_0\right)=0.998 \mathrm{~g} \mathrm{~cm}^{-3}\)
Density of water at \(4^{\circ} \mathrm{C},\left(f_4\right)=1.000 \mathrm{~g} \mathrm{~cm}-3\)
Change in temperature, \((\Delta t)=4^{\circ} \mathrm{C}\)
Let the average coefficient of volume expansion of water in the temperature range of 0 to \(4^{\circ} \mathrm{C}\) be \(\gamma\).
Weknow \(: f_4=f_0(1+\gamma \Delta t)\)
\(
\begin{aligned}
& \Rightarrow f_0=\frac{f_4}{1+\gamma \Delta t} \\
& \Rightarrow 0.998=\frac{1}{1+\gamma .4} \\
& \Rightarrow 1+4 \gamma=\frac{1}{0.998} \\
& \Rightarrow 4 \gamma=\left(\frac{1}{0.998}\right)-1 \\
& \Rightarrow \gamma=0.0005=5 \times 10^{-4 o} \mathrm{C}^{-1}
\end{aligned}
\)
As the density decreases,
\(
\gamma=-5 \times 10^{-4 o} \mathrm{C}^{-1}
\)
Therefore,the average coefficient of volume expansion of water in the temperature range of 0 to \(4^{\circ} \mathrm{C}\) will be
\(
\gamma=-5 \times 10^{-4}
\) -
Question 73 of 88
73. Question
Find the ratio of the lengths of an iron rod and an aluminium rod for which the difference in the lengths is independent of temperature. Coefficients of linear expansion of iron and aluminium are \(12 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\) and \(23 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\) respectively.
CorrectIncorrectHint
Let the original length of iron rod be \(L_{F e}\) and \(L_{F e}\) be its length when temperature is increased by \(\Delta T\).
Let the original length of aluminium rod be \(L_{A l}\) and \(L_{A l}^{\prime}\) be its length when temperature is increased by \(\Delta T\).
Coefficient of linear expansion of iron,
\(
\alpha_{F e}=12 \times 10^{-6}{ }^{\circ} \mathrm{C}-1\)
Coefficient of linear expansion of aluminium, \(\alpha_{\mathrm{Al}}=23 \times 10^{-6}{ }^{\circ} \mathrm{C}-1\)
Since the difference in length is independent of temperature, the difference is always constant.
\(
\begin{aligned}
& L_{F e}^{\prime}=L_{F e}\left(1+\alpha_{F e} \times \Delta T\right) \\
& \text { and } L_{A l}^{\prime}=L_{A l}\left(1+\alpha_{A l} \times \Delta T\right) \\
& \Rightarrow L_{F e}^{\prime}-L_{A l}^{\prime}=L_{F e}-L_{A l}+L_{F e} \times \alpha_{F e} \Delta T-L_{A l} \times \alpha_{A l} \times \Delta T \quad-(1)
\end{aligned}
\)
Given :
\(
L_{F e}^{\prime}-L_{A l}^{\prime}=L_{F e}-L_{A l}
\)
Hence, \(L_{F e} \alpha_{F e}=L_{A l} \alpha_{A l}\)[using(1)]
\(
\Rightarrow \frac{L_{F e}}{L_{A l}}=\frac{23}{12}
\)
The ratio of the lengths of the iron to the aluminium rod is \(23: 12\). -
Question 74 of 88
74. Question
A pendulum clock gives correct time at \(20^{\circ} \mathrm{C}\) at a place where \(g=9.800 \mathrm{~m} \mathrm{~s}^{-2}\). The pendulum consists of a light steel rod connected to a heavy ball. It is taken to a different place where \(g=9.788 \mathrm{~m} \mathrm{~s}^{-2}\). At what temperature will it give correct time? Coefficient of linear expansion of steel \(=12 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\).
CorrectIncorrectHint
Given: The temperature at which the pendulum shows the correct time, \(T_1=20^{\circ} \mathrm{C}\) Coefficient of linear expansion of steel,
\(
\alpha=12 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}
\)
Let \(T_2\) be the temperature at which the value of \(\mathrm{g}\) is \(9.788 \mathrm{~ms}^{-2}\) and
\(\Delta \mathrm{T}\) be the change in temperature.
So, the time periods of pendulum at different values of \(g\) will be \(t_1\) and \(t_2\), such that
\(
\begin{aligned}
& t_1=2 \pi \sqrt{\frac{l_1}{g_1}} \\
& t_2=2 \pi \sqrt{\frac{l_2}{g_2}} \\
& =\frac{2 \pi \sqrt{l_1(1+\alpha \Delta T)}}{\sqrt{g_2}}\left(\because l_2=l_1(1+\alpha \Delta T)\right)
\end{aligned}
\)
Given, \(t_1=t_2\)
\(
\begin{aligned}
& \Rightarrow \frac{2 \pi \sqrt{l_1}}{\sqrt{g_1}}=\frac{2 \pi \sqrt{l_1(1+\alpha \Delta T)}}{\sqrt{g_2}} \\
& \Rightarrow \sqrt{\left(\frac{l_1}{g_1}\right)}=\frac{\sqrt{l_1(1+\alpha \Delta T)}}{\sqrt{g_2}} \\
& \Rightarrow \frac{1}{9.8}=\frac{1+12 \times 10^{-6} \times \Delta T}{9.788} \\
& \Rightarrow \frac{9.788}{9.8}=1+12 \times 10^{-6} \times \Delta T \\
& \Rightarrow \frac{9.788}{9.8}-1=12 \times 10^{-6} \times \Delta T \\
& \Rightarrow \Delta T=\frac{-0.00122}{12 \times 10^{-6}} \\
& \Rightarrow T_2-20=-102.4 \\
& \Rightarrow T_2=-102.4+20 \\
& =-82^{\circ} 4 \\
& \Rightarrow T_2 \approx-82^{\circ} \mathrm{C}
\end{aligned}
\)
Therefore, for a pendulum clock to give correct time, the temperature at which the value of \(\mathrm{g}\) is \(9.788 \mathrm{~ms}^{-2}\) should be \(-82^{\circ} \mathrm{C}\) -
Question 75 of 88
75. Question
An aluminium plate fixed in a horizontal position has a hole of diameter \(2.000 \mathrm{~cm}\). A steel sphere of diameter \(2.005 \mathrm{~cm}\) rests on this hole. All the lengths refer to a temperature of \(10^{\circ} \mathrm{C}\). The temperature of the entire system is slowly increased. At what temperature will the ball fall down? Coefficient of linear expansion of aluminium is \(23 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\) and that of steel is \(11 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\)
CorrectIncorrectHint
Given:
Diameter of the steel sphere at temperature \(\left(T_1=10^{\circ} \mathrm{C}\right), d_{s t}=2.005 \mathrm{~cm}\)
Diameter of the aluminium sphere, \(\mathrm{d}_{\mathrm{Al}}=2.000 \mathrm{~cm}\)
Coefficient of linear expansion of steel, \(\alpha_{\text {st }}=11 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\)
Coefficient of linear expansion of aluminium, \(\alpha_{\mathrm{Al}}=23 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\)
Let the temperature at which the ball will fall be \(T_2\) so that change in temperature be \(\Delta T\).
\(
\begin{aligned}
& d_{s t}^{\prime}=2.005\left(1+\alpha_{s t} \Delta T\right) \\
& \Rightarrow d_{s t}^{\prime}=2.005+2.005 \times 11 \times 10^{-6} \times \Delta T \\
& d_{A l}^{\prime}=2\left(1+\alpha_{A l} \times \Delta T\right) \\
& \Rightarrow d_{A l}^{\prime}=2+2 \times 23 \times 10^{-6} \times \Delta T
\end{aligned}
\)
The steel ball will fall when both the diameters become equal.
So, \(d_{\mathrm{st}}^{\prime}=d_{\mathrm{Al}}^{\prime}\)
\(
\begin{aligned}
& \Rightarrow 2.005+2.005 \times 11 \times 10^{-6} \Delta T=2+2 \times 23 \times 10^{-6} \Delta T \\
& \Rightarrow(46-22.055) \times 10^{-6} \Delta T=0.005 \\
& \Rightarrow \Delta T=\frac{0.005 \times 10^6}{23.945}=208.81 \\
& \text { Now, } \Delta T=T_2-T_1=T_2-10^{\circ} \mathrm{C} \\
& \Rightarrow T_2=\Delta T+T_1=208.81+10 \\
& \Rightarrow T_2=218.8 \cong 219^{\circ} \mathrm{C}
\end{aligned}
\)
Therefore, the temperature at which the ball will fall is \(219^{\circ} \mathrm{C}\). -
Question 76 of 88
76. Question
A glass window is to be fit in an aluminium frame. The temperature on the working day is \(40^{\circ} \mathrm{C}\) and the glass window measures exactly \(20 \mathrm{~cm} \times 30 \mathrm{~cm}\). What should be the size of the aluminium frame so that there is no stress on the glass in winter even if the temperature drops to \(0^{\circ} \mathrm{C}\)? Coefficients of linear expansion for glass and aluminium are \(9.0 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\) and \(24 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\) respectively.
CorrectIncorrectHint
Given:
At \(40^{\circ} \mathrm{C}\), the length and breadth of the glass window are \(20 \mathrm{~cm}\) and \(30 \mathrm{~cm}\), respectively. Coefficient of linear expansion of glass,
\(
\alpha_g=9.0 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}
\)
Coefficient of linear expansion for aluminium,
\(
\alpha_{A l}=24 \times 100^{-6}{ }^{\circ} \mathrm{C}^{-1}
\)
The final length of aluminium should be equal to the final length of glass so that there is no stress on the glass in winter, even if the temperature drops to \(0^{\circ} \mathrm{C}\).
Change in temperature,
\(
\Delta \theta=40^{\circ} \mathrm{C}
\)
Let the initial length of aluminium be I.
\(
\begin{aligned}
& l\left(1-\alpha_{A l} \Delta \theta\right)=20\left(1-\alpha_g \Delta \theta\right) \\
& \Rightarrow l\left(1-24 \times 10^{-6} \times 40\right)=20\left(1-9 \times 10^{-6} \times 40\right) \\
& \Rightarrow l(1-0.00096)=20(1-0.00036) \\
& \Rightarrow l=\frac{20 \times 0.99964}{1-0.00096} \\
& =\frac{20 \times 0.99964}{0.99904} \\
& \Rightarrow l=20.012 \mathrm{~cm}
\end{aligned}
\)
Let the initial breadth of aluminium be \(b\).
\(
\begin{aligned}
& b\left(1-\alpha_{A l} \Delta \theta\right)=30\left(1-\alpha_g \Delta \theta\right) \\
& \Rightarrow b=\frac{30 \times\left(1-9 \times 10^{-6} \times 40\right)}{\left(1-24 \times 10^{-6} \times 40\right)} \\
& =\frac{30 \times 0.99964}{0.99904} \\
& \Rightarrow b=30.018 \mathrm{~cm}
\end{aligned}
\)
Therefore, the size of the aluminium frame should be \(20.012 \mathrm{~cm} \times 30.018 \mathrm{~cm}\). -
Question 77 of 88
77. Question
The volume of a glass vessel is \(1000 \mathrm{cc}\) at \(20^{\circ} \mathrm{C}\). What volume of mercury should be poured into it at this temperature so that the volume of the remaining space does not change with temperature? Coefficients of cubical expansion of mercury and glass are \(1.8 \times 10^{-4}{ }^{\circ} \mathrm{C}^{-1}\) and \(9.0 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\) respectively.
CorrectIncorrectHint
At \(\mathrm{T}=20^{\circ} \mathrm{C}\), the volume of the glass vessel, \(\mathrm{V}_{\mathrm{g}}=1000 \mathrm{cc}\).
Let the volume of mercury be \(\mathrm{V}_{\mathrm{Hg}}\).
Coefficient of cubical expansion of mercury, \(\gamma_{\mathrm{Hg}}=1.8 \times 10^{-4} /{ }^{\circ} \mathrm{C}\)
Coefficient of cubical expansion of glass, \(\gamma_g=9 \times 10^{-6} /{ }^{\circ} \mathrm{C}\)
Change in temperature, \(\Delta T\), is same for glass and mercury.
Let the volume of glass and mercury after rise in temperature be \(\mathrm{V}^{\prime} \mathrm{g}\) and \(\mathrm{V}^{\prime} \mathrm{Hg}\) respectively.[/latex]
Volume of remaining space after change in temperature, \(
\left(V_g^{\prime}-V^{\prime}{ }_{H g}\right)=
\)Volume of the remaining space (initial), \(\left(\mathrm{V}_{\mathrm{g}}-\mathrm{V}_{\mathrm{Hg}}\right)\)
We know: \(V_g^{\prime}=V_g\left(1+V_g \Delta T\right)\)
\(
V^{\prime}{ }_{H g}=V_{H g}\left(1+Y_{H g} \Delta T\right)
\)
Subtracting (2) from (1), we get:
\(
\begin{aligned}
& V_g^{\prime}-V_{H g}^{\prime}=V_g-V_{H g}+V_g \gamma_g \Delta T-V_{H g} \gamma_{H g} \Delta T \\
& \Rightarrow V_g \gamma_g \Delta T-V_{H g} \gamma_{H g} \Delta T=0 \\
& \Rightarrow \frac{V_g}{V_{H g}}=\frac{\gamma_{H g}}{\gamma_g} \\
& \Rightarrow \frac{1000}{V_{H g}}=\frac{1.8 \times 10^{-4}}{9 \times 10^{-6}} \\
& \Rightarrow V_{H g}=\frac{9 \times 10^{-3}}{1.8 \times 10^{-4}} \\
& \Rightarrow V_{H g}=50 c c
\end{aligned}
\)
Therefore, the volume of mercury that should be poured into the glass vessel is \(50 \mathrm{cc}\). -
Question 78 of 88
78. Question
An aluminium can of cylindrical shape contains \(500 \mathrm{~cm}^3\) of water. The area of the inner cross section of the can is \(125 \mathrm{~cm}^2\). All measurements refer to \(10^{\circ} \mathrm{C}\). Find the rise in the water level if the temperature increases to \(80^{\circ} \mathrm{C}\). The coefficient of linear expansion of aluminium \(=23 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\) and the average coefficient of volume expansion of water \(=3.2 \times 10^{-4}{ }^{\circ} \mathrm{C}^{-1}\) respectively.
CorrectIncorrectHint
Given:
Volume of water contained in the aluminium can, \(V_0=500 \mathrm{~cm}^3\)
Area of inner cross-section of the can, \(A=125 \mathrm{~cm}^2\)
Coefficient of volume expansion of water, \(\gamma=3.2 \times 10^{-4}{ }^{\circ} \mathrm{C}^{-1}\)
Coefficient of linear expansion of aluminium,
\(
\alpha_{A L}=23 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}
\)
If \(\Delta \theta\) is the change in temperature, then final volume of water
\((V)\) due to expansion,
\(
\begin{aligned}
V & =V_0(1+\gamma \Delta \theta) \\
& =500\left[1+3.2 \times 10^{-4} \times(80-10)\right] \\
& =500\left[1+3.2 \times 10^{-4} \times 70\right] \\
& =511.2 \mathrm{~cm}^3
\end{aligned}
\)
The aluminium vessel expands in its length only.
So, area of expansion of the base can be neglected.
Increase in volume of water \(=11.2 \mathrm{~cm}^3\)
Consider a cylinder of volume \(11.2 \mathrm{~cm}^3\)
\(\therefore\) Increase in height of the water
\(
\begin{aligned}
& =\frac{11.2}{125}=0.0896 \\
& =0.089 \mathrm{~cm}
\end{aligned}
\) -
Question 79 of 88
79. Question
A glass vessel measures exactly \(10 \mathrm{~cm} \times 10 \mathrm{~cm} \times 10 \mathrm{~cm}\) at \(0^{\circ} \mathrm{C}\). It is filled completely with mercury at this temperature. When the temperature is raised to \(10^{\circ} \mathrm{C}\), \(1.6 \mathrm{~cm}^3\) of mercury overflows. Calculate the coefficient of volume expansion of mercury. Coefficient of linear expansion of glass \(=6.5 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\)
CorrectIncorrectHint
Given: At \(0^{\circ} \mathrm{C}\), volume of glass vessel, \(\mathrm{V}_{\mathrm{g}}=10 \times 10 \times 10=1000 \mathrm{cc}=\) volume of mercury, \(\mathrm{V}_{\mathrm{Hg}}\) Let the volume of mercury at \(10^{\circ} \mathrm{C}\) be \(\mathrm{V}^{\prime} \mathrm{Hg}\) and that of glass be \(\mathrm{V}^{\prime} \mathrm{g}\).
At \(10^{\circ} \mathrm{C}\), the additional volume of mercury than glass, due to heating, \(\mathrm{V}^{\prime} \mathrm{Hg}-\mathrm{V}^{\prime} \mathrm{g}=1.6 \mathrm{~cm}^3\)
So change in temperature, \(\Delta \mathrm{T}=10^{\circ} \mathrm{C}\)
Coefficient of linear expansion of glass, \(\alpha_g=6.5 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\)\(
\text { Therefore, the coefficient of volume expansion of glass, } \gamma_g=3 \times 6.5 \times 10^{-6{ }^{\circ}} \mathrm{C}^{-1}
\)
Let the coefficient of volume expansion of mercury be \(\gamma_{\mathrm{Hg}}\).
We know that
\(
\begin{aligned}
& \mathrm{V}^{\prime}{ }_{\mathrm{Hg}}=\mathrm{V}_{\mathrm{Hg}}\left(1+\gamma_{\mathrm{Hg}} \Delta \mathrm{T}\right) \dots(1)\\
& \mathrm{V}_{\mathrm{g}}^{\prime}=\mathrm{V}_{\mathrm{g}}\left(1+\gamma_{\mathrm{g}} \Delta \mathrm{T}\right) \dots(2)
\end{aligned}
\)
Subtracting (2) from (1) we get,
\(
\begin{aligned}
& \mathrm{V}^{\prime} \mathrm{Hg}-\mathrm{V}_{\mathrm{g}}^{\prime}=\mathrm{V}_{\mathrm{Hg}}-\mathrm{V}_{\mathrm{g}}+\mathrm{V}_{\mathrm{Hg}} \gamma_{\mathrm{Hg}} \Delta \mathrm{T}-\mathrm{V}_{\mathrm{g}} \gamma_{\mathrm{g}} \Delta \mathrm{T} \text { (as } \mathrm{V}_{\mathrm{Hg}}=\mathrm{V}_{\mathrm{g}} \text { ) } \\
& \Rightarrow 1.6=1000 \times \gamma_{H g} \times 10-1000 \times 6.5 \times 3 \times 10^{-6} \times 10 \\
& \Rightarrow \gamma_{H g}=\frac{1.6+19.5 \times 10^{-2}}{10000} \\
& \Rightarrow \gamma_{H g}=\frac{1.6+0.195}{10000} \\
& \Rightarrow \gamma_{H g}=\frac{1.795}{10000} \\
& \Rightarrow \gamma_{H g}=1.795 \times 10^{-4} \\
& \Rightarrow \gamma_{\mathrm{Hg}} \cong 1.8 \times 10^{-4{ }^{\circ}} \mathrm{C}^{-1}
\end{aligned}
\)
Therefore, the coefficient of volume expansion of mercury is \(1.8 \times 10^{-4}{ }^{\circ} \mathrm{C}^{-1}\). -
Question 80 of 88
80. Question
The densities of wood and benzene at \(0^{\circ} \mathrm{C}\) are \(880 \mathrm{~kg} \mathrm{~m}^3\) and \(900 \mathrm{~kg} \mathrm{~m}^{-3}\) respectively. The coefficients of volume expansion are \(1.2 \times 10^{-3}{ }^{\circ} \mathrm{C}^{-1}\) for wood and \(1.5 \times 10^{-3} \circ \mathrm{C}^{-1}\) for benzene. At what temperature will a piece of wood just sink in benzene?
CorrectIncorrectHint
\(
\begin{aligned}
& f_{\mathrm{w}}=880 \mathrm{Kg} / \mathrm{m}^3, f_{\mathrm{b}}=900 \mathrm{Kg} / \mathrm{m}^3 \\
& \mathrm{~T}_1=0^{\circ} \mathrm{C}, \\
& \gamma_\omega=1.2 \times 10^{-3} /{ }^{\circ} \mathrm{C} \\
& \gamma_{\mathrm{b}}=1.5 \times 10^{-3} /{ }^{\circ} \mathrm{C} \\
& \text { The sphere begins } \mathrm{t} \text { sink when, } \\
& (\mathrm{mg})_{\text {sphere }}=\text { displaced water } \\
& \Rightarrow \mathrm{V} f_\omega^{\prime} \mathrm{g}=\mathrm{V} f_b^{\prime} \mathrm{g} \\
& \Rightarrow \frac{f_\omega}{1+\gamma_\omega \Delta \theta}=\frac{f_{\mathrm{b}}}{1+\gamma_{\mathrm{b}} \Delta \theta} \\
& \Rightarrow \frac{880}{1+1.2 \times 10^{-3} / \theta}={ }^{\circ} \mathrm{C} \\
& \Rightarrow 880+880 \times 1.5 \times 10^{-3}(\Delta \theta)=900+900 \times 1.2 \times 10^{-3}(\Delta \theta) \\
& \Rightarrow\left(880 \times 1.5 \times 10^{-3}-900 \times 1.2 \times 10^{-3}\right)(\Delta \theta)=20 \\
& \Rightarrow(1320-1080) \times 10^{-3}(\Delta \theta)=20 \\
& \Rightarrow \Delta \theta=83.3^{\circ} \mathrm{C} \approx 83^{\circ} \mathrm{C}
\end{aligned}
\) -
Question 81 of 88
81. Question
A steel rod of length \(1 \mathrm{~m}\) rests on a smooth horizontal base. If it is heated from \(0^{\circ} \mathrm{C}\) to \(100^{\circ} \mathrm{C}\), what is the longitudinal strain developed?
CorrectIncorrectHint
The steel rod is resting on a horizontal base at \(0^{\circ} \mathrm{C}\). When the temperature is increased to \(100^{\circ} \mathrm{C}\), it will lead to an increase in the length of the steel due to expansion on heating. Since there is no opposition in the expansion of length, no longitudinal strain will be developed.
-
Question 82 of 88
82. Question
A steel rod is clamped at its two ends and rests on a fixed horizontal base. The rod is unstrained at \(20^{\circ} \mathrm{C}\). Find the longitudinal strain developed in the rod if the temperature rises to \(50^{\circ} \mathrm{C}\). Coefficient of linear expansion of steel \(=1.2 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}\).
CorrectIncorrectHint
Given, \(\theta_1=20^{\circ} \mathrm{C}, \quad \theta_2=50^{\circ} \mathrm{C}\)
\(
a_{\text {steel }}=1.2 \times 10^{-5} /{ }^{\circ} \mathrm{C}
\)
Longitudinal strain \(=\)?
Strain \(=\frac{\Delta L}{L}-\frac{L a \Delta \theta}{L}=a \Delta \theta\)
\(=1.2 \times 10^{-5} \times(50-20)\)
\(=1.2 \times 10^{-5} \times 30\)
\(=36 \times 10^{-5}=3.6 \times 10^{-4}\)
The strain is opposite to the direction of expansion. -
Question 83 of 88
83. Question
A steel wire of cross-sectional area \(0.5 \mathrm{~mm}^2\) is held between two fixed supports. If the wire is just taut at \(20^{\circ} \mathrm{C}\), determine the tension when the temperature falls to \(0^{\circ} \mathrm{C}\). Coefficient of linear expansion of steel is \(1.2 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}\) and its Young’s modulus is \(2.0 \times 10^{11} \mathrm{~N} \mathrm{~m}^{-2}\).
CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{A}=0.5 \mathrm{~mm}^2=0.5 \times 10^{-6} \mathrm{~m}^2 \\
& \mathrm{~T}_1=20^{\circ} \mathrm{C}, \mathrm{T}_2=0^{\circ} \mathrm{C} \\
& \alpha_{\mathrm{s}}=1.2 \times 10^{-5} /{ }^{\circ} \mathrm{C}, \quad \gamma=2 \times 2 \times 10^{11} \mathrm{~N} / \mathrm{m}^2
\end{aligned}
\)
Decrease in length due to compression \(=L \alpha \Delta \theta\)
\(
\gamma=\frac{\text { Stress }}{\text { Strain }}=\frac{\mathrm{F}}{\mathrm{A}} \times \frac{\mathrm{L}}{\Delta \mathrm{L}} \Rightarrow \Delta \mathrm{L}=\frac{\mathrm{FL}}{\mathrm{A\gamma}}
\)
Tension is developed due to (1) & (2) Equating them,
\(
\begin{aligned}
& L \alpha \Delta \theta=\frac{F L}{A \gamma} \Rightarrow F=\alpha \Delta \theta A \gamma \\
& =1.2 \times 10^{-5} \times(20-0) \times 0.5 \times 10^{-5} 2 \times 10^{11}=24 \mathrm{~N}
\end{aligned}
\) -
Question 84 of 88
84. Question
A steel rod is rigidly clamped at its two ends. The rod is under zero tension at \(20^{\circ} \mathrm{C}\). If the temperature rises to \(100^{\circ} \mathrm{C}\), what force will the rod exert on one of the clamps? Area of cross section of the rod=\(2.00 \mathrm{~mm}^2\), Coefficient of linear expansion of steel \(=12.0 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\) and Young’s modulus of steel \(=2.00 \times 10^{11} \mathrm{~N} \mathrm{~m}^{-2}\).
CorrectIncorrectHint
Given:
Temperature of the rod at zero tension, \(T_1=20^{\circ} \mathrm{C}\)
Final temperature, \(T_2=100^{\circ} \mathrm{C}\)
Change in temperature, \(\Delta \theta=80^{\circ} \mathrm{C}\)
Cross-sectional area of the rod, \(A=2 \mathrm{~mm}^2=2 \times 10^{-6} \mathrm{~m}^2\)
Coefficient of linear expansion of steel, \(\alpha=12 \times 10^{-6}{ }^{\circ} \mathrm{C}^{-1}\)
Young’s modulus of steel, \(Y=2 \times 10^{11} \mathrm{Nm}^{-2}\)
Let \(L\) be the length of the steel rod at \(20^{\circ} \mathrm{C}\) and \(L^{\prime}\) be the length of steel rod at \(100^{\circ} \mathrm{C}\).
Change of length of the rod, \(\Delta L=L^{\prime}-L\)
If \(F\) be the force exerted by the rod on one of the clamps due to rise in temperature, then
\(
\begin{aligned}
& \mathrm{Y}=\frac{\text { stress }}{\text { strain }}=\frac{\mathrm{F}}{\mathrm{A}} / \frac{\Delta \mathrm{L}}{\mathrm{L}} \\
& \Rightarrow \mathrm{F}=\frac{\mathrm{Y} \times \Delta \mathrm{L}}{\mathrm{L}} \times \mathrm{A} \\
& \Delta \mathrm{L}=\mathrm{L} \alpha \Delta \theta \\
& \Rightarrow \mathrm{F}=\frac{\mathrm{YL} \alpha \Delta \theta \mathrm{A}}{\mathrm{L}} \\
& \mathrm{F}=\mathrm{YA} \alpha \Delta \theta \\
& =2 \times 10^{11} \times 2 \times 10^{-6} \times 12 \times 10^{-6} \times 80 \\
& =48 \times 80 \times 10^{-1}
\end{aligned}
\)
So, \(F=384 \mathrm{~N}\)
Therefore, the rod will exert a force of \(384 \mathrm{~N}\) on one of the clamps. -
Question 85 of 88
85. Question
A steel ball initially at a pressure of \(1.0 \times 10^5 \mathrm{~Pa}\) is heated from \(20^{\circ} \mathrm{C}\) to \(120^{\circ} \mathrm{C}\) keeping its volume constant. Find the pressure inside the ball. Coefficient of linear expansion of steel \(=12 \times 10^{-6} \mathrm{C}^{-1}\) and bulk modulus of steel \(=1.6 \times 10^{11} \mathrm{~N} \mathrm{~m}^{-2}\).
CorrectIncorrectHint
Given:
Initial pressure on the steel ball \(=1.0 \times 10^5 \mathrm{~Pa}\)
The ball is heated from \(20^{\circ} \mathrm{C}\) to \(120^{\circ} \mathrm{C}\).
So, change in temperature, \(\Delta \theta=100^{\circ} \mathrm{C}\).
Coefficient of linear expansion of steel, \(\alpha=12 \times 10^{-6 \circ} \mathrm{C}^{-1}\)
Bulk modulus of steel,\(B=1.6 \times 10^{11} \mathrm{Nm}^{-2}\)
Pressure is given as,
\(
\begin{aligned}
& \Rightarrow P=B \times \gamma \Delta \theta \\
& \Rightarrow P=B \times 3 \alpha \Delta \theta(\because \gamma=3 \alpha) \\
& \Rightarrow P=1.6 \times 10^{11} \times 3 \times 12 \times 10^{-6} \times(120-20) \\
& =1.6 \times 3 \times 12 \times 10^{11} \times 10^{-6} \times 10^2 \\
& =57.6 \times 10^7 \\
& \Rightarrow P=5.8 \times 10^8 \mathrm{~Pa}
\end{aligned}
\)
Therefore, the pressure inside the ball is \(5.8 \times 10^8 \mathrm{~Pa}\). -
Question 86 of 88
86. Question
The moment of inertia of a solid body of any shape changes with temperature as \(I=I_0(1+2 \alpha \theta)\), where \(I_0\) is the moment of inertia at \(0^{\circ} \mathrm{C}\) and \(\alpha\) is the coefficient of linear expansion of the solid. Is this true?
CorrectIncorrectHint
Given:
Coefficient of linear expansion of solid \(=\alpha\)
Moment of inertia at \(0{ }^{\circ} \mathrm{C}=I_0\)
If temperature changes to \(\theta\) from \(0^{\circ} \mathrm{C}\), then change in temperature, \((\Delta \mathrm{T})=\theta\)
Let I be the new moment of inertia attained due to rise in temperature.
Let \(R_0\) be the radius of gyration at \(0{ }^{\circ} \mathrm{C}\).
We know that on heating, radius of gyration will change as
\(
R=R_0(1+\alpha \theta)
\)
Here, \(R\) is the radius of gyration after heating.
\(\mathrm{I}_0=\mathrm{MR}_0{ }^2\), where \(\mathrm{M}=\) mass of the body
Now, I \(=\mathrm{MR}^2=\mathrm{MR}_0^2(1+\alpha \theta)^2\)
Expanding binomially and neglecting the higher terms of \(\operatorname{order}(\alpha \theta)\) that will be very small, we get \(\mathrm{I}=\mathrm{MR}_0{ }^2(1+2 \alpha \theta)\)
So, \(I=I_0(1+2 \alpha \theta)\)
Hence, proved. -
Question 87 of 88
87. Question
A torsional pendulum consists of a solid disc connected to a thin wire \(\left(\alpha=2.4 \times 10^{-5} \mathrm{C}^{-1}\right)\) at its centre. Find the percentage change in the time period between peak winter \(\left(5^{\circ} \mathrm{C}\right)\) and peak summer \(\left(45^{\circ} \mathrm{C}\right)\).
CorrectIncorrectHint
Let the initial M.I.a at \(0^{\circ} \mathrm{C}\) be \(\mathrm{I}_0\)
\(
\begin{aligned}
& \mathrm{T}=2 \pi \sqrt{\frac{\mathrm{I}}{\mathrm{K}}} \\
& \mathrm{I}=\mathrm{I}_0(1+2 \alpha \Delta \theta) \quad \text { (from above question) }
\end{aligned}
\)
At \(5^{\circ} \mathrm{C}, \quad T_1=2 \pi \sqrt{\frac{I_0(1+2 \alpha \Delta \theta)}{K}}=2 \pi \sqrt{\frac{I_0(1+2 \alpha 5)}{K}}=2 \pi \sqrt{\frac{I_0(1+10 \alpha)}{\mathrm{K}}}\)
At \(45^{\circ} \mathrm{C}, \quad T_2=2 \pi \sqrt{\frac{\mathrm{I}_0(1+2 \alpha 45)}{\mathrm{K}}}=2 \pi \sqrt{\frac{\mathrm{I}_0(1+90 \alpha)}{\mathrm{K}}}\)
\(
\frac{T_2}{T_1}=\sqrt{\frac{1+90 \alpha}{1+10 \alpha}}=\sqrt{\frac{1+90 \times 2.4 \times 10^{-5}}{1+10 \times 2.4 \times 10^{-5}}} \sqrt{\frac{1.00216}{1.00024}}
\)
\(\%\) change \(=\left(\frac{T_2}{T_1}-1\right) \times 100=0.0959 \%=9.6 \times 10^{-2}\) -
Question 88 of 88
88. Question
A circular disc made of iron is rotated about its axis at a constant velocity \(\omega\). Calculate the percentage change in the linear speed of a particle of the rim as the disc is slowly heated from \(20^{\circ} \mathrm{C}\) to \(50^{\circ} \mathrm{C}\) keeping the angular velocity constant. Coefficient of linear expansion of iron \(=1 \cdot 2 \times 10^{-5}{ }^{\circ} \mathrm{C}^{-1}\)
CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{T}_1=20^{\circ} \mathrm{C}, \mathrm{T}_2=50^{\circ} \mathrm{C}, \Delta \mathrm{T}=30^{\circ} \mathrm{C} \\
& \alpha=1.2 \times 10^5 /{ }^{\circ} \mathrm{C}
\end{aligned}
\)
\(\omega\) remains constant
(I) \(\omega=\frac{V}{R}\)
(II) \(\omega=\frac{V^{\prime}}{R^{\prime}}\)
Now, \(R^{\prime}=R(1+\alpha \Delta \theta)=R+R \times 1.2 \times 10^{-5} \times 30=1.00036 R\)
From (I) and (II)
\(
\begin{aligned}
& \frac{V}{R}=\frac{V^{\prime}}{R^{\prime}}=\frac{V^{\prime}}{1.00036 R} \\
& \Rightarrow V^{\prime}=1.00036 \mathrm{~V} \\
& \% \text { change }=\frac{(1.00036 \mathrm{~V}-\mathrm{V})}{\mathrm{V}} \times 100=0.00036 \times 100=3.6 \times 10^{-2}
\end{aligned}
\)