1. The basic property of a fluid is that it can flow. The fluid does not have any resistance to change of its shape. Thus, the shape of a fluid is governed by the shape of its container.
2. A liquid is incompressible and has a free surface of its own. A gas is compressible and it expands to occupy all the space available to it.
3. If \(F\) is the normal force exerted by a fluid on an area \(A\) then the average pressure \(P_{a v}\) is defined as the ratio of the force to the area
   \(
   P_{a v}=\frac{F}{A}
   \)
4. The unit of pressure is the pascal (Pa). It is the same as \(\mathrm{N} \mathrm{m}^{-2}\). Other common units of pressure are
   \(
   \begin{aligned}
   & 1 \mathrm{~atm}=1.01 \times 10^5 \mathrm{~Pa} \\
   & 1 \mathrm{bar}=10^5 \mathrm{~Pa} \\
   & 1 \mathrm{torr}=133 \mathrm{~Pa}=0.133 \mathrm{kPa} \\
   & 1 \mathrm{~mm} \text { of } \mathrm{Hg}=1 \text { torr }=133 \mathrm{~Pa}
   \end{aligned}
   \)
5. Pascal’s law states that: Pressure in a fluid at rest is the same at all points which are at the same height. A change in pressure applied to an enclosed fluid is transmitted undiminished to every point of the fluid and the walls of the containing vessel.
6. The pressure in a fluid varies with depth \(\mathrm{h}\) according to the expression
   \(
   P=P_{\mathrm{a}}+\rho g h
   \)
   where \(\rho\) is the density of the fluid, assumed uniform.
7. The volume of an incompressible fluid passing any point every second in a pipe of nonuniform cross-section is the same in the steady flow.
   \(v A=\) constant ( \(v\) is the velocity and \(A\) is the area of crossection)
   The equation is due to mass conservation in incompressible fluid flow.
8. Bernoulli’s principle states that as we move along a streamline, the sum of the pressure \((P)\), the kinetic energy per unit volume \(\left(\rho v^2 / 2\right)\) and the potential energy per unit volume \((\rho g y)\) remains a constant.
   \(P+\rho v^2 / 2+\rho g y=\) constant
   The equation is basically the conservation of energy applied to nonviscous fluid motion in a steady state. There is no fluid that has zero viscosity, so the above statement is true only approximately. The viscosity is like friction and converts the kinetic energy to heat energy.
9. Though shear strain in a fluid does not require shear stress, when shear stress is applied to a fluid, motion is generated which causes a shear strain growing with time. The ratio of the shear stress to the time rate of shearing strain is known as the coefficient of viscosity, \(\eta\).
   where symbols have their usual meaning and are defined in the text.
10. Stokes’ law states that the viscous drag force \(\mathbf{F}\) on a sphere of radius a moving with velocity \(\mathbf{v}\) through a fluid of viscosity is, \(\mathbf{F}=6 \pi \eta a v\).
11. Surface tension is a force per unit length (or surface energy per unit area) acting in the plane of interface between the liquid and the bounding surface. It is the extra energy that the molecules at the interface have as compared to the interior.

Points to Remember

1. Pressure is a scalar quantity. The definition of pressure as “force per unit area” may give one false impression that pressure is a vector. The “force” in the numerator of the definition is the component of the force normal to the area upon which it is impressed. While describing fluids as a concept, a shift from particle and rigid body mechanics is required. We are concerned with properties that vary from point to point in the fluid.
2. One should not think of the pressure of a fluid as being exerted only on a solid like the walls of a container or a piece of solid matter immersed in the fluid. Pressure exists at all points in a fluid. An element of a fluid (such as the one shown in Fig. 10.2) is in equilibrium because the pressures exerted on the various faces are equal.
3. The expression for pressure
   \(
   P=P_{\mathrm{a}}+\rho g h
   \)
   holds true if fluid is incompressible. Practically speaking it holds for liquids, which are largely incompressible and hence is a constant with height.
4. The gauge pressure is the difference of the actual pressure and the atmospheric pressure. \(P-P_{\mathrm{a}}=P_{\mathrm{g}}\)
   Many pressure-measuring devices measure the gauge pressure. These include the tire pressure gauge and the blood pressure gauge (sphygmomanometer).
5. A streamline is a map of fluid flow. In a steady flow, two streamlines do not intersect as it means that the fluid particle will have two possible velocities at the point.
6. Bernoulli’s principle does not hold in presence of viscous drag on the fluid. The work done by this dissipative viscous force must be taken into account in this case, and \(P_2\) [Flg. 10.9] will be lower than the value given by Eq. (10.12).
7. As the temperature rises the atoms of the liquid become more mobile and the coefficient of viscosity, \(\eta\) falls. In a gas, the temperature rise increases the random motion of atoms, and \(\eta\) increases.
8. Surface tension arises due to the excess potential energy of the molecules on the surface in comparison to their potential energy in the interior. Such a surface energy is present at the interface separating two substances at least one of which is a fluid. It is not the property of a single fluid alone.

Exercises 10.1: Explain why
(a) The blood pressure in humans is greater at the feet than at the brain
(b) Atmospheric pressure at a height of about 6 km decreases to nearly half of its value at sea level, though the height of the atmosphere is more than 100 km
(c) Hydrostatic pressure is a scalar quantity even though the pressure is force divided by area.

Solution:

(a) The height of the blood column is more for the feet as compared to that for the brain.
Consequently, the blood pressure in humans is greater at the feet than at the brain.
(b) The variation of air density with height is not linear. So, pressure also does not reduce linearly with height. The air pressure at a height \(h\) is given by \(P=P_0 e^{-\alpha h}\) where \(P_0\) represents the pressure of air at sea level and \(\alpha\) is a constant.
(c) Due to the applied force on the liquid, the pressure is transmitted equally in all directions inside the liquid. That is why there is no fixed direction for the pressure due to liquid. Hence hydrostatic pressure is a scalar quantity.

Exercises 10.2: Explain why (a) The angle of contact of mercury with glass is obtuse, while that of water
with glass is acute.
(b) Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
(c) Surface tension of a liquid is independent of the area of the surface (d) Water with detergent dissolved in it should have small angles of contact.
(e) A drop of liquid under no external forces is always spherical in shape

Solution: 

(a) Let a drop of a liquid \(L\) be poured on a solid surface \(S\) placed in the air \(A\). If \(T_{S L}\), and \(T_{S A}\) be the surface tensions corresponding to the solid-liquid layer, liquid-air layer, and solid-air layer respectively and \(\theta\) be the angle of contact between the liquid and solid, then

\(
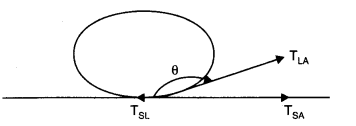
\begin{aligned}
& T_{L A} \cos \theta+T_{S L}=T_{S A} \\
& \Rightarrow \cos \theta=T_{S A}-T_{S L} / T_{L A}
\end{aligned}
\)
For the mercury-glass interface, \(T_{S A}<T_{S L}\). Therefore, \(\cos 0\) is negative. Thus \(\theta\) is an obtuse angle. For the water-glass interface, \(T_{S A}>T_{S L}\). Therefore \(\cos 0\) is positive. Thus, \(\theta\) is an acute angle.

(b) Water on a clean glass surface tends to spread out i.e., water wets glass because the force of cohesion of water is much less than the force of adhesion due to glass. In the case of mercury force of cohesion due to mercury molecules is quite strong as compared to the adhesion force due to glass. Consequently, mercury does not the wet glass and tends to form drops.

(c) Surface tension of the liquid is the force acting per unit length on a line drawn tangentially to the liquid surface at rest. Since \(h\) as force is independent of the area of the liquid surface, therefore, surface tension is also independent of the area of the liquid surface.

(d) We know that clothes have narrow pores or spaces which act as capillaries. Also, we know that the rise of liquid in a capillary tube is directly proportional to \(\cos \theta\) (Here \(\theta\) is the angle of contact). As \(\theta\) is small for detergent, therefore \(\cos \theta\) will be large. Due to this, the detergent will penetrate more in the narrow pores of the clothes.

(e) We know that any system tends to remain in a state of minimum energy. In the absence of any external force for a given volume of liquid its surface area and consequently. Surface energy is the least for a spherical shape. It is due to this reason that a liquid drop, in the absence of an external force is spherical in shape.

Exercises 10.3: Fill in the blanks using the word(s) from the list appended with each statement:

(a) Surface tension of liquids generally . . . with temperatures (increases/decreases)
(b) Viscosity of gases . . . with temperature, whereas viscosity of liquids . . . with temperature (increases/decreases)
(c) For solids with elastic modulus of rigidity, the shearing force is proportional to . . . , while for fluids it is proportional to . .. (shear strain/rate of shear strain)
(d) For a fluid in a steady flow, the increase in flow speed at a constriction follows (conservation of mass / Bernoulli’s principle)
(e) For the model of a plane in a wind tunnel, turbulence occurs at a … speed for turbulence for an actual plane (greater / smaller)

Solution:

(a) decreases
(b) increases; decreases
(c) shear strain; rate of shear strain
(d) conservation of mass; Bernoulli’s principle
(e) greater.

Exercises 10.4: Explain why
(a) To keep a piece of paper horizontal, you should blow over, not under, it
(b) When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers
(c) The size of the needle of a syringe controls the flow rate better than the thumb the pressure exerted by a doctor while administering an injection
(d) A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel
(e) A spinning cricket ball in the air does not follow a parabolic trajectory

Solution:

(a) When we blow over the piece of paper, the velocity of air increases. As a result, the pressure on it decreases in accordance with Bernoulli’s theorem whereas the pressure below remains the same (atmospheric pressure). Thus, the paper remains horizontal.
(b) By doing so the area of the outlet of the water jet is reduced, so the velocity of water increases according to the equation of continuity \(av =\) constant.
(c) For a constant height, Bernoulli’s theorem is expressed as \(P+1 / 2 \rho v^2=\) Constant
In this equation, the pressure \(P\) occurs with a single power whereas the velocity occurs with a square power. Therefore, the velocity has more effect compared to the pressure. It is for this reason that the needle of the syringe controls the flow rate better than the thumb pressure exerted by the doctor.
(d) This is because of the principle of conservation of momentum. While the flowing fluid carries forward momentum, the vessel gets a backward momentum.
(e) A spinning cricket ball would have followed a parabolic trajectory has there been no air. But because of air, the Magnus effect takes place. Due to the Magnus effect, the spinning cricket ball deviates from its parabolic trajectory.