7.13 Angular momentum in case of rotation about a fixed axis

We already know from there that the time rate of the total angular momentum of a system of particles about a point is equal to the total external torque on the system taken about the same point. When the total external torque is zero, the total angular momentum of the system is conserved. We now wish to study the angular momentum in the special case of rotation about a fixed axis. The general expression for the total angular momentum of the system of \(n\) particles is
\(
\mathbf{L}=\sum_{i=1}^N \mathbf{r}_i \times \mathbf{p}_i \dots(7.25b)
\)
We first consider the angular momentum of a typical particle of the rotating rigid body. We then sum up the contributions of individual particles to get \(\mathbf{L}\) of the whole body.

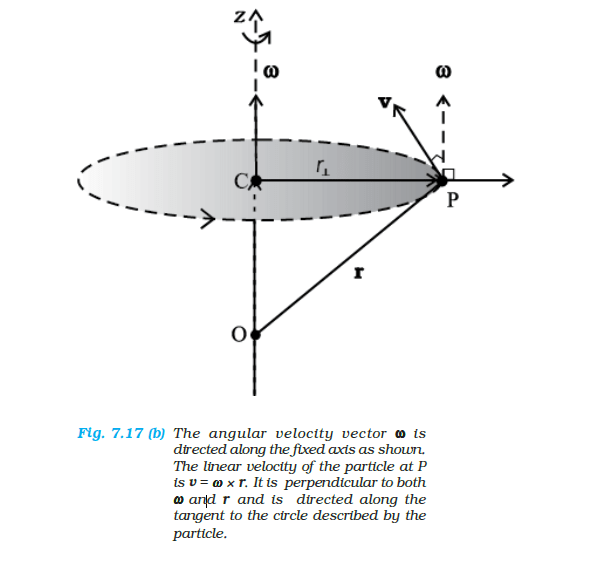
For a typical particle \(l=\mathbf{r} \times \mathbf{p}\). As seen in the last section \(\mathbf{r}=\mathbf{O P}=\mathbf{O C}+\mathbf{C P}\) [Fig. 7.17(b)]. With \(\mathbf{p}=\mathrm{m} \mathbf{v},\)
\(
\boldsymbol{l}=(\mathbf{O C} \times m \mathbf{v})+(\mathbf{C P} \times m \mathbf{v})
\)
The magnitude of the linear velocity \(\mathbf{v}\) of the particle at \(\mathrm{P}\) is given by \(v=\omega r_{\perp}\) where \(r_{\perp}\) is the length of \(\mathrm{CP}\) or the perpendicular distance of \(P\) from the axis of rotation. Further, \(\mathbf{v}\) is tangential at \(P\) to the circle which the particle describes. Using the right-hand rule one can check that \(\mathbf{C P} \times \mathbf{v}\) is parallel to the fixed axis. The unit vector along the fixed axis (chosen as the \(z\)-axis) is \(\hat{\mathbf{k}}\). Hence
\(
\begin{aligned}
& \mathbf{C P} \times m \mathbf{v}=r_{\perp}(m v) \hat{\mathbf{k}} \\
& =m r_{\perp}^2 \omega \hat{\mathbf{k}} \quad \text { (since } v=\omega r_{\perp})
\end{aligned}
\)
Similarly, we can check that \(\mathbf{O C} \times \mathbf{v}\) is perpendicular to the fixed axis. Let us denote the part of \(l\) along the fixed axis (1.e. the \(z\)-axis) by \(l_z\), then
\(
\boldsymbol{l}_{\mathrm{z}}=\mathbf{C P} \times m \mathbf{v}=m r_{\perp}^2 \omega \hat{\mathbf{k}}
\)
and \(\boldsymbol{l}=\boldsymbol{l}_z+\mathbf{O C} \times m \mathbf{v}\)
We note that \(l_z\) is parallel to the fixed axis, but \(l\) is not. In general, for a particle, the angular momentum \(l\) is not along the axis of rotation, i.e. for a particle, \(l\) and \(\boldsymbol{\omega}\) are not necessarily parallel. Compare this with the corresponding fact in translation. For a particle, \(\mathbf{p}\) and \(\mathbf{v}\) are always parallel to each other.

For computing the total angular momentum of the whole rigid body, we add up the contribution of each particle of the body.
Thus \(\quad \mathbf{L}=\sum \boldsymbol{l}_i=\sum \boldsymbol{l}_{i z}+\sum \mathbf{O C}_i \times m_i \mathbf{v}_i\)
We denote by \(\mathbf{L}_{\perp}\) and \(\mathbf{L}_z\) the components of
\(\mathbf{L}\) respectively perpendicular to the z-axis and along the \(z\)-axis;
\(
\mathbf{L}_{\perp}=\sum \mathbf{O} \mathbf{C}_t \times m_t \mathbf{v}_t \dots(7.44a)
\)
where \(m_i\) and \(\mathbf{v}_1\) are respectively the mass and the velocity of the \(t^{\text {th }}\) particle and \(\mathrm{C}_1\) is the centre of the circle described by the particle;
and \(\quad \mathbf{L}_z=\sum \boldsymbol{l}_{i z}=\left(\sum_i m_i r_i^2\right) w \mathbf{k}\)
or \(\quad \mathbf{L}_z=I \omega \hat{\mathbf{k}} \dots(7.44b)\)
The last step follows since the perpendicular distance of the \(i^{\text {th }}\) particle from the axis is \(r_i\); and by definition, the moment of inertia of the body about the axis of rotation is \(I=\sum m_i r_i^2\).
Note \(\mathbf{L}=\mathbf{L}_z+\mathbf{L}_{\perp} \dots(7.44c)\)

The rigid bodies which we have mainly considered in this chapter are symmetric about the axis of rotation, 1.e. the axis of rotation is one of their symmetry axes. For such bodies, for a given \(\mathbf{O C}\), for every particle which has a velocity \(\mathbf{v}_i\), there is another particle of velocity \(-\mathbf{v}_i\) located diametrically opposite on the circle with centre \(\mathrm{C}_i\) described by the particle. Together such pairs will contribute zero to \(\mathbf{L}_{\perp}\) and as a result for symmetric bodies \(\mathbf{L}_{\perp}\) is zero, and hence
\(
\mathbf{L}=\mathbf{L}_{\mathrm{z}}=I \omega \hat{\mathbf{k}} \dots(7.44d)
\)
For bodies, which are not symmetric about the axis of rotation, \(\mathbf{L}\) is not equal to \(\mathbf{L}_z\) and hence \(\mathbf{L}\) does not lie along the axis of rotation. Referring to Table 7.1, can you tell in which cases \(\mathbf{L}=\mathbf{L}_{\mathrm{z}}\) will not apply?

Let us differentiate Eq. (7.44b). Since \(\hat{\mathbf{k}}\) is a fixed (constant) vector, we get
\(
\frac{\mathrm{d}}{\mathrm{d} t}\left(\mathbf{L}_z\right)=\left(\frac{\mathrm{d}}{\mathrm{d} t}(I \omega)\right) \hat{\mathbf{k}}
\)
Now, Eq. (7.28b) states
\(
\frac{\mathrm{d} \mathbf{L}}{\mathrm{d} t}=\boldsymbol{\tau}
\)
As we have seen in the last section, only those components of the external torques which are along the axis of rotation, need to be taken into account, when we discuss rotation about a fixed axis. This means we can take \(\boldsymbol{\tau}=\tau \hat{\mathbf{k}}\).
Since \(\mathbf{L}=\mathbf{L}_z+\mathbf{L}_{\perp}\) and the direction of \(\mathbf{L}_{\mathrm{z}}\) (vector \(\hat{\mathbf{k}}\) ) is fixed, it follows that for rotation about a fixed axis,
\(
\begin{aligned}
& \frac{\mathrm{d} \mathbf{L}_{\mathrm{z}}}{\mathrm{d} t}=\tau \hat{\mathbf{k}} \dots(7.45a)\\
& \text { and } \frac{\mathrm{d} \mathbf{L}_{\perp}}{\mathrm{d} t}=0 \dots(7.45b)
\end{aligned}
\)
Thus, for rotation about a fixed axis, the component of angular momentum perpendicular to the fixed axis is constant. As \(\mathbf{L}_z=I \omega \hat{\mathbf{k}}\), we get from Eq. (7.45a),
\(
\frac{\mathrm{d}}{\mathrm{d} t}(I \omega)=\tau \dots(7.45c)
\)
If the moment of inertia \(I\) does not change with time,
\(
\frac{\mathrm{d}}{\mathrm{d} t}(I \omega)=I \frac{\mathrm{d} \omega}{\mathrm{d} t}=I \alpha
\)
and we get from Eq. (7.45c),
\(
\tau=I \alpha \dots(7.43)
\)
We have already derived this equation using the work-kinetic energy route.

Conservation of angular momentum

We are now in a position to revisit the principle of conservation of angular momentum in the context of rotation about a fixed axis. From Eq. (7.45c), if the external torque is zero,
\(
L_{\mathrm{z}}=I \omega=\text { constant } \dots(7.46)
\)
For symmetric bodies, from Eq. (7.44d), \(L_z\) may be replaced by \(L\). \(\left(L\right.\) and \(L_z\) are respectively the magnitudes of \(\mathbf{L}\) and \(\mathbf{L}_{\mathrm{z}}\).)
This then is the required form, for fixed axis rotation, of Eq. (7.29a), which expresses the general law of conservation of angular momentum of a system of particles. Eq. (7.46) applies to many situations that we come across in daily life.

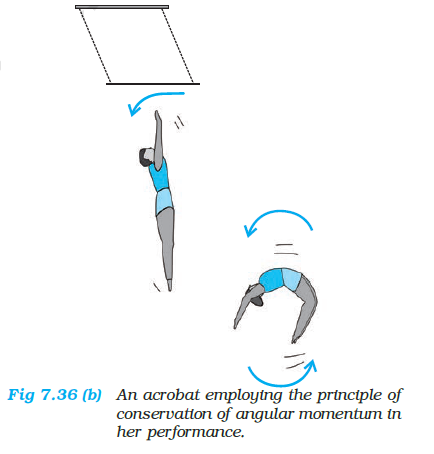
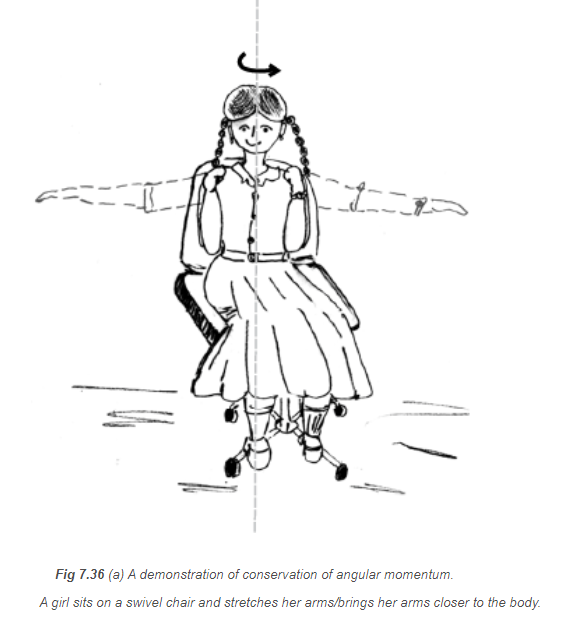
You may do this experiment with your friend. Sit on a swivel chair (a chair with a seat, free to rotate about a pivot) with your arms folded and feet not resting on, i.e., away from, the ground. Ask your friend to rotate the chair rapidly. While the chair is rotating with considerable angular speed stretch your arms horizontally. What happens? Your angular speed is reduced. If you bring back your arms closer to your body, the angular speed increases again. This is a situation where the principle of conservation of angular momentum is applicable. If friction in the rotational mechanism is neglected, there is no external torque about the axis of rotation of the chair and hence \(I \omega\) is constant. Stretching the arms increases \(I\) about the axis of rotation, resulting in decreasing the angular speed \(\omega\). Bringing the arms closer to the body has the opposite effect.

A circus acrobat and a diver take advantage of this principle. Also, skaters and classical, Indian or western, dancers performing a pirouette (a spinning about a tip-top) on the toes of one-foot display ‘mastery’ over this principle.