7.8 Equilibrium of a rigid body

A rigid body is said to be in mechanical equilibrium, if both its linear momentum and angular momentum are not changing with time, or equivalently, the body has neither linear acceleration nor angular acceleration. This means

• the total force, i.e. the vector sum of the forces, on the rigid body is zero;
  \(
  \mathbf{F}_1+\mathbf{F}_2+\ldots+\mathbf{F}_n=\sum_{i=1}^n \mathbf{F}_i=\mathbf{0} \dots(7.30a)
  \)
  If the total force on the body is zero, then the total linear momentum of the body does not change with time. Eq. (7.30a) gives the condition for the translational equilibrium of the body.

• The total torque, i.e. the vector sum of the torques on the rigid body is zero,
  \(
  \boldsymbol{\tau_1}+\boldsymbol{\tau_2}+\ldots+\boldsymbol{\tau_n}=\sum_{i=1}^n \boldsymbol{\tau_i}=\mathbf{0}
  \)
  If the total torque on the rigid body is zero, the total angular momentum of the body does not change with time. Eq. \((7.30\) b) gives the condition for the rotational equilibrium of the body.

The centre of mass of a body remains in equilibrium if the total external force acting on the body is zero. This follows from the equation \(F=M a\). Similarly, a body remains in rotational equilibrium if the total external torque acting on the body is zero. This follows from the equation \(\tau=I \alpha\). Thus, if a body remains at rest in an inertial frame, the total external force acting on the body should be zero in any direction and the total external torque should be zero about any line.

We shall often find situations in which all the forces acting on a body lie in a single plane as shown in the figure below.

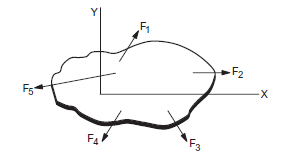
Let us take this plane as the \(X-Y\) plane. For translational equilibrium
\(
\begin{aligned}
& \sum F_x=0 \dots(i)\\
& \sum F_y=0 \dots(ii)
\end{aligned}
\)
As all the forces are in the \(X\) – \(Y\) plane, \(F_z\) is identically zero for each force and so \(\sum F_z=0\) is automatically satisfied. Now consider rotational equilibrium. The torque of each force about the \(X\)-axis is identically zero because either the force intersects the axis or it is parallel to it. Similarly, the torque of each force about the \(Y\)-axis is identically zero. In fact, the torque about any line in the \(X-Y\) plane is zero.
Thus, the condition of rotational equilibrium is
\(
\sum \tau_z=0 \dots(iii)
\)

We can generalize this result to \(n\) forces as shown below.
Eq. (7.30a) and Eq. (7.30b), both, are vector equations. They are equivalent to three scalar equations each. Eq. (7.30a) corresponds to

\(
\sum_{i=1}^n F_{i x}=0, \sum_{i=1}^n F_{i y}=0 \text { and } \sum_{i=1}^n F_{i z}=0 \dots(7.31a)
\)
where \(F_{i x}, F_{i y}\) and \(F_{i z}\) are respectively the \(x, y\) and \(z\) components of the forces \(\mathbf{F}_i\) Similarly, Eq. (7.30b) is equivalent to three scalar equations
\(
\sum_{i=1}^n \tau_{i x}=0, \sum_{i=1}^n \tau_{i y}=0 \text { and } \sum_{i=1}^n \tau_{i z}=0 \dots(7.31b)
\)
where \(\tau_{i x} \tau_{i y}\) and \(\tau_{i z}\) are respectively the \(x, y\) and \(z\) components of the torque \(\boldsymbol\tau_i\).

The equilibrium of a body is called stable if the body tries to regain its equilibrium position after being slightly displaced and released. It is called unstable if it gets further displaced after being slightly displaced and released. If it can stay in equilibrium even after being slightly displaced and released, it is said to be in neutral equilibrium.

A body may be in partial equilibrium, i.e., it may be in translational equilibrium and not in rotational equilibrium, or it may be in rotational equilibrium and not in translational equilibrium.

Here are some examples, Consider a light (i. e. of negligible mass) rod (AB) as shown in Fig. 7.20(a). At the two ends (A and B) of which two parallel forces, both equal in magnitude and acting along same direction are applied perpendicular to the rod.

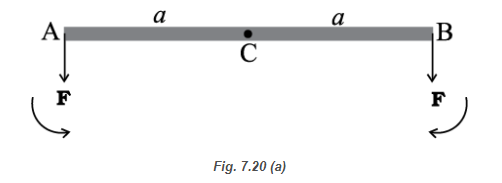
Let \(\mathrm{C}\) be the midpoint of \(\mathrm{AB}, \mathrm{CA}=\mathrm{CB}=a\). the moment of the forces at A and \(B\) will both be equal in magnitude \((a F)\), but opposite in sense as shown. The net moment on the rod will be zero. The system will be in rotational equilibrium, but it will not be in translational equilibrium; \(\sum \mathbf{F} \neq \mathbf{0}\)

The force at B in Fig. 7.20(a) is reversed in Fig. 7.20(b). Thus, we have the same rod with two forces of equal magnitude but acting in opposite directions applied perpendicular to the rod, one at end A and the other at end B. Here the moments of both the forces are equal, but they are not opposite; they act in the same sense and cause anticlockwise rotation of the rod. The total force on the body is zero; so the body is in translational equilibrium, but it is not in rotational equilibrium. Although the rod is not fixed in any way, it undergoes pure rotation (i.e. rotation without translation).

A pair of forces of equal magnitude but acting in opposite directions with different lines of action is known as a couple or torque. A couple produces rotation without translation.

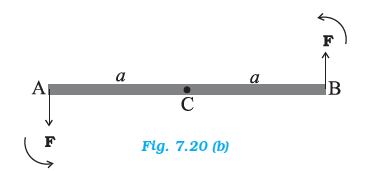
When we open the lid of a bottle by turning it, our fingers are applying a couple to the lid [Fig. 7.21(a)]. Another known example is a compass needle in the earth’s magnetic field as shown in the Fig. 7.21(b). The earth’s magnetic field exerts equal forces on the north and south poles. The force on the North Pole is towards the north, and the force on the South Pole is toward the south. Except when the needle points in the north-south direction; the two forces do not have the same line of action. Thus there is a couple acting on the needle due to the earth’s magnetic field.

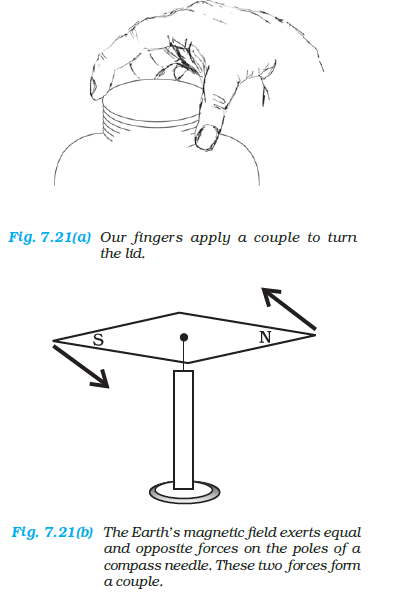
Example 7.13: Show that moment of a couple does not depend on the point about which you take the moments.

Solution:

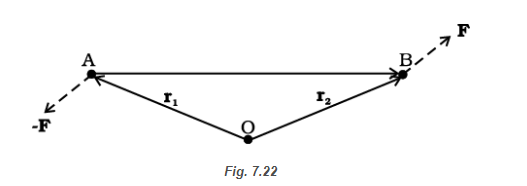
Consider a couple as shown in Fig. 7.22 acting on a rigid body. The forces \(\mathbf{F}\) and \(-\mathbf{F}\) act respectively at points \(B\) and \(A\). These points have position vectors \(\mathbf{r}_1\) and \(\mathbf{r}_2\) with respect to origin O. Let us take the moments of the forces about the origin.
The moment of the couple \(=\) sum of the moments of the two forces making the couple
\(
\begin{aligned}
& =\mathbf{r}_1 \times(-\mathbf{F})+\mathbf{r}_2 \times \mathbf{F} \\
& =\mathbf{r}_2 \times \mathbf{F}-\mathbf{r}_1 \times \mathbf{F} \\
& =\left(\mathbf{r}_2-\mathbf{r}_1\right) \times \mathbf{F}
\end{aligned}
\)
But \(\mathbf{r}_1+\mathbf{A B}=\mathbf{r}_2\), and hence \(\mathbf{A B}=\mathbf{r}_2-\mathbf{r}_1\).
The moment of the couple, therefore, is \(\mathbf{A B} \times \mathbf{F}\)

Clearly, this is independent of the origin, the point about which we took the moments of the forces.

Principle of moments

An ideal lever is essentially a light (i.e. of negligible mass) rod pivoted at a point along its length. This point is called the fulcrum. A seesaw on the children’s playground is a typical example of a lever. Two forces \(F_1\) and \(F_2\), parallel to each other and usually perpendicular to the lever, as shown here, act on the lever at distances \(d_1\) and \(d_2\) respectively from the fulcrum as shown in Fig. 7.23.

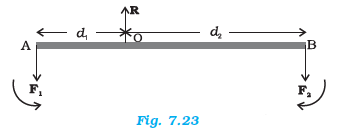
The lever is a system in mechanical equilibrium. Let \(\mathbf{R}\) be the reaction of the support at the fulcrum; \(\mathbf{R}\) is directed opposite to the forces \(F_1\) and \(F_2\). For translational equilibrium,
\(
R-F_1-F_2=0 \dots(i)
\)
For considering rotational equilibrium we take the moments about the fulcrum; the sum of moments must be zero,
\(
d_1 F_1-d_2 F_2=0 \dots(ii)
\)
Normally the anticlockwise (clockwise) moments are taken to be positive (negative). Note \(R\) acts at the fulcrum itself and has zero moment about the fulcrum.
In the case of the lever force \(F_1\) is usually some weight to be lifted. It is called the load and its distance from the fulcrum \(d_1\) is called the load arm. Force \(\mathrm{F}_2\) is the effort applied to lift the load; distance \(d_2\) of the effort from the fulcrum is the effort arm.
Eq. (ii) can be written as
\(
d_1 F_1=d_2 F_2 \dots(7.32a)
\)
or load arm \(\times\) load \(=\) effort \(\operatorname{arm} \times\) effort
The above equation expresses the principle of moments for a lever. Incidentally the ratio \(F_1 / F_2\) is called the Mechanical Advantage (M.A.);
\(
\text { M.A. }=\frac{F_1}{F_2}=\frac{d_2}{d_1} \dots(7.32b)
\)
If the effort arm \(d_2\) 1s larger than the load arm, the mechanical advantage is greater than one. Mechanical advantage greater than one means that a small effort can be used to lift a large load. There are several examples of a lever around you besides the see-saw. The beam of a balance is a lever.

Centre of gravity

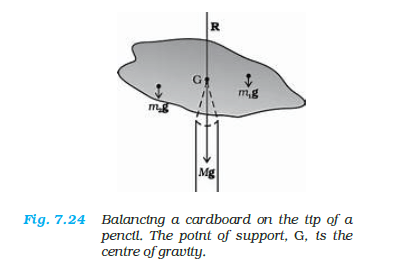
Figure 7.24 illustrates a similar experiment that you can easily perform. Take an irregular-shaped cardboard having mass \(M\) and a narrow-tipped object like a pencil. You can locate by trial and error a point \(\mathrm{G}\) on the cardboard where it can be balanced on the tip of the pencil. (The cardboard remains horizontal in this position.) This point of balance is the centre of gravity (CG) of the cardboard. The tip of the pencil provides a vertically upward force due to which the cardboard is in mechanical equilibrium. As shown in the F1g. 7.24, the reaction of the tip is equal and opposite to \(M g\) and hence the cardboard is in translational equilibrium. It is also in rotational equilibrium; if it were not so, due to the unbalanced torque it would tilt and fall. There are torques on the cardboard due to the forces of gravity like \(m_1 g, m_2 g . .\). etc, acting on the individual particles that make up the cardboard.

The CG of the cardboard is so located that the total torque on it due to the forces \(m_1 g, m_2 g\) \(\ldots\). etc. is zero.

If \(\mathbf{r}_i\) is the position vector of the \(i\) th particle of an extended body with respect to its CG, then the torque about the \(\mathrm{CG}\), due to the force of gravity on the particle is \(\tau_i=\mathbf{r}_i \times m_i\) g. The total gravitational torque about the CG is zero, i.e.
\(
\boldsymbol\tau_g=\sum \boldsymbol\tau_i=\sum \mathbf{r}_i \times m_i \mathbf{g}=\mathbf{0} \dots(7.33)
\)
We may, therefore, define the CG of a body as that point where the total gravitational torque on the body is zero.

We notice that in Eq. (7.33), g is the same for all particles, and hence it comes out of the summation. This gives, since \(\mathbf{g}\) is non-zero, \(\sum m_i \mathbf{r}_i=\mathbf{0}\). Remember that the position vectors \(\left(\mathbf{r}_{i}\right)\) are taken with respect to the CG. If the sum is zero, the origin must be the centre of mass of the body. Thus, the centre of gravity of the body coincides with the centre of mass in uniform gravity or gravity-free space. We note that this is true because the body being small, \(g\) does not vary from one point of the body to the other. If the body is so extended that g varies from part to part of the body, then the centre of gravity and centre of mass will not coincide. Basically, the two are different concepts. The centre of mass has nothing to do with gravity. It depends only on the distribution of mass of the body.

Determining the centre of gravity of a body of irregular shape

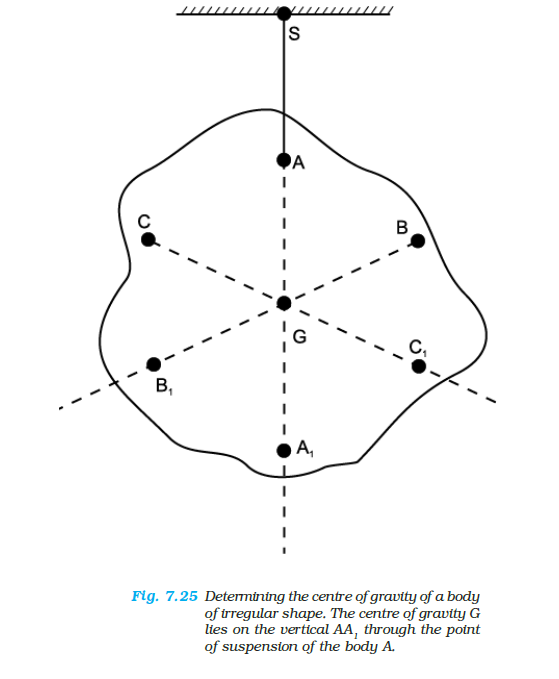
Figure 7.25 illustrates another way of determining the CG of an irregular shaped body like a cardboard. If you suspend the body from some point like A, the vertical line through A passes through the CG. We mark the vertical \(A_1\). We then suspend the body through other points like \(\mathrm{B}\) and \(\mathrm{C}\). The intersection of the verticals gives the CG. Explain why the method works. Since the body is small enough, the method allows us to determine also its centre of mass.

Example 7.14: A metal bar \(70 \mathrm{~cm}\) long and \(4.00 \mathrm{~kg}\) in mass supported on two knife-edges placed \(10 \mathrm{~cm}\) from each end. A \(6.00 \mathrm{~kg}\) load is suspended at \(30 \mathrm{~cm}\) from one end. Find the reactions at the knife-edges. (Assume the bar to be of uniform cross-section and homogeneous.)

Solution:

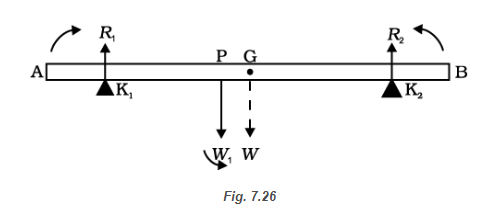
Figure 7.26 shows the rod \(\mathrm{AB}\), the positions of the knife edges \(K_1\) and \(K_2\), the centre of gravity of the rod at \(\mathrm{G}\) and the suspended load at \(\mathrm{P}\).

Note the weight of the rod \(W\) acts at its centre of gravity \(\mathrm{G}\). The rod is uniform in cross section and homogeneous; hence \(\mathrm{G}\) is at the centre of the rod; \(\mathrm{AB}=70 \mathrm{~cm} . \mathrm{AG}=35 \mathrm{~cm}, \mathrm{AP}\) \(=30 \mathrm{~cm}, \mathrm{PG}=5 \mathrm{~cm}, \mathrm{AK}_1=\mathrm{BK}_2=10 \mathrm{~cm}\) and \(\mathrm{K}_1 \mathrm{G}\) \(=\mathrm{K}_2 \mathrm{G}=25 \mathrm{~cm}\). Also, \(W=\) weight of the \(\operatorname{rod}=\)
\(4.00 \mathrm{~kg}\) and \(W_1=\) suspended load \(=6.00 \mathrm{~kg} ;\) \(R_1\) and \(R_2\) are the normal reactions of the support at the knife edges.
For translational equilibrium of the rod,
\(
R_1+R_2-W_1-W=0 \dots(i)
\)
Note \(W_1\) and \(W\) act vertically down and \(R_1\) and \(R_2\) act vertically up.

For considering rotational equilibrium, we take moments of the forces. A convenient point to take moments about is G. The moments of \(R_2\) and \(W_1\) are anticlockwise (+ve), whereas the moment of \(\mathrm{R}_1\) is clockwise (-ve).
For rotational equilibrium,
\(
-R_1\left(\mathrm{~K}_1 \mathrm{G}\right)+W_1(\mathrm{PG})+R_2\left(\mathrm{~K}_2 \mathrm{G}\right)=0 \dots(ii)
\)
It is given that \(W=4.00 \mathrm{~g} \mathrm{~N}\) and \(W_1=6.00 \mathrm{~g}\)
\(\mathrm{N}\), where \(g=\) acceleration due to gravity. We take \(g=9.8 \mathrm{~m} / \mathrm{s}^2\).
With numerical values inserted, from (i)
\(
\begin{aligned}
& R_1+R_2-4.00 g-6.00 g=0 \\
& \text { or } R_1+R_2=10.00 g \mathrm{~N} \dots(iii)\\
&=98.00 \mathrm{~N}
\end{aligned}
\)
From (ii), \(-0.25 R_1+0.05 W_1+0.25 R_2=0\) or \(R_1-R_2=1.2 g \mathrm{~N}=11.76 \mathrm{~N} \dots(iv)\)
From (iii) and (iv), \(R_1=54.88 \mathrm{~N}\),
\(
R_2=43.12 \mathrm{~N}
\)
Thus the reactions of the support are about \(55 \mathrm{~N}\) at \(\mathrm{K}_1\) and \(43 \mathrm{~N}\) at \(\mathrm{K}_2\).

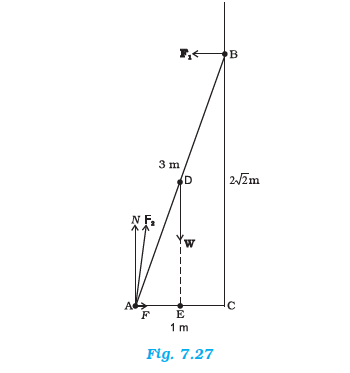
Example 7.15: A \(3 \mathrm{~m}\) long ladder weighing \(20 \mathrm{~kg}\) leans on a frictionless wall. Its feet rest on the floor \(1 \mathrm{~m}\) from the wall as shown in Fig.7.27. Find the reaction forces of the wall and the floor.

Solution:

The ladder \(\mathrm{AB}\) is \(3 \mathrm{~m}\) long, its foot \(\mathrm{A}\) is at distance \(\mathrm{AC}=1 \mathrm{~m}\) from the wall. From Pythagoras theorem, \(\mathrm{BC}=2 \sqrt{2} \mathrm{~m}\). The forces on the ladder are its weight W acting at its centre of gravity D, reaction forces \(F_1\) and \(F_2\) of the wall and the floor respectively. Force \(F_1\) is perpendicular to the wall, since the wall is frictionless. Force \(F_2\) is resolved into two components, the normal reaction \(N\) and the force of friction \(F\). Note that \(F\) prevents the ladder from sliding away from the wall and is therefore directed toward the wall.

For translational equilibrium, taking the forces in the vertical direction,
\(
N-W=0 \dots(i)
\)
Taking the forces in the horizontal direction,
\(
F-F_1=0 \dots(ii)
\)
For rotational equilibrium, taking the moments of the forces about A,
\(
2 \sqrt{2} F_1-(1 / 2) W=0 \dots(iii)
\)
Now \(\quad W=20 \mathrm{~g}=20 \times 9.8 \mathrm{~N}=196.0 \mathrm{~N}\)
From (1) \(N=196.0 \mathrm{~N}\)
From (iii) \(F_1=W / 4 \sqrt{2}=196.0 / 4 \sqrt{2}=34.6 \mathrm{~N}\)
From (ii) \(F=F_1=34.6 \mathrm{~N}\)
\(
F_2=\sqrt{F^2+N^2}=199.0 \mathrm{~N}
\)
The force \(F_2\) makes an angle \(\alpha\) with the horizontal,
\(
\tan \alpha=N / F=4 \sqrt{2}, \alpha=\tan ^{-1}(4 \sqrt{2}) \approx 80^{\circ}
\)