Two Particle system and its center of mass

Consider two particles \(A\) and \(B\) of masses \(m_1\) and \(m_2\) respectively. Take the line joining \(A\) and \(B\) as the \(X\)-axis. Let the coordinates of the particles at time \(t\) be \(x_1\) and \(x_2\). Suppose no external force acts on the two-particle system. The particles \(A\) and \(B\), however, exert forces on each other and the particles accelerate along the line joining them. Suppose the particles are initially at rest and the force between them is attractive. The particles will then move along the line \(A B\) as shown in the figure below.

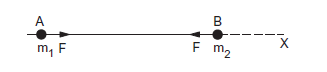
The centre of mass at time \(t\) is situated at
\(
X=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}
\)
As time passes, \(x_1, x_2\) change and hence \(X\) changes and the centre of mass moves along the \(X\)-axis. Velocity of the centre of mass at time \(t\) is
\(
V_{C M}=\frac{d x}{d t}=\frac{m_1 v_1+m_2 v_2}{m_1+m_2} \dots(i)
\)
The acceleration of the centre of mass is
\(
a_{C M}=\frac{d V_{C M}}{d t}=\frac{m_1 a_1+m_2 a_2}{m_1+m_2} \dots(ii)
\)
Suppose the magnitude of the forces between the particles is \(F\). As the only force acting on \(A\) is \(F\) towards \(B\), its acceleration is \(a_1=F / m_1\). The force on \(B\) is \((-F)\) and hence \(a_2=-F / m_2\)
Putting in (ii),
\(
a_{C M}=\frac{m_1\left(F / m_1\right)+m_2\left(-F / m_2\right)}{m_1+m_2}=0 .
\)
That means, the velocity of the centre of mass does not change with time. But as we assumed, initially the particles are at rest. Thus, at this instant, \(v_1=v_2=0\) and \(V_{C M}=0\). Hence the centre of mass remains fixed and does not change with time.

Thus, if no external force acts on a two-particle system and its centre of mass is at rest (say in the inertial frame A) initially, it remains fixed (in the inertial frame A) even when the particles individually move and accelerate. Let us now generalise this result.

Example 7.6: Two charged particles of masses \(m\) and \(2 m\) are placed a distance \(d\) apart on a smooth horizontal table. Because of their mutual attraction, they move towards each other and collide. Where will the collision occur with respect to the initial positions?

Solution: As the table is smooth, there is no friction. The weight of the particles and the normal force balance each other as there is no motion in the vertical direction. Thus, taking the two particles as constituting the system, the sum of the external forces acting on the system is zero. The forces of attraction between the particles are the internal forces as we have included both the particles in the system. Therefore, the centre of mass of the system will have no acceleration.
Initially, the two particles are placed on the table and their velocities are zero. The velocity of the centre of mass is, therefore, zero. As time passes, the particles move, but the centre of mass will continue to be at the same place. At the time of collision, the two particles are at one place and the centre of mass will also be at that place. As the centre of mass does not move, the collision will take place at the centre of mass.
The centre of mass will be at a distance \(2 d / 3\) from the initial position of the particle of mass \(m\) towards the other particle and the collision will take place there.

n Particle system and its center of mass

Let \(\mathbf{r}_i\) be the position vector of the \(i^{\text {th }}\) particle and \(\mathbf{R}\) be the position vector of the centre of mass:
\(
\mathbf{r}_i=x_i \hat{\mathbf{i}}+y_i \hat{\mathbf{j}}+z_i \hat{\mathbf{k}}
\)
and \(\mathbf{R}=X \hat{\mathbf{i}}+Y \hat{\mathbf{j}}+Z \hat{\mathbf{k}}\)
Then \(\mathbf{R}=\frac{\sum m_i \mathbf{r}_i}{M}\)
We may rewrite the above equation as
\(
M \mathbf{R}=\sum m_i \mathbf{r}_i=m_1 \mathbf{r}_1+m_2 \mathbf{r}_2+\ldots+m_n \mathbf{r}_n \dots(7.7)
\)
Differentiating the two sides of the equation with respect to time we get
\(
\begin{aligned}
& M \frac{\mathrm{d} \mathbf{R}}{\mathrm{d} t}=m_1 \frac{\mathrm{d} \mathbf{r}_1}{\mathrm{~d} t}+m_2 \frac{\mathrm{d} \mathbf{r}_2}{\mathrm{~d} t}+\ldots+m_n \frac{\mathrm{d} \mathbf{r}_n}{d t} \\
& \text { or } \\
& M \mathbf{V}=m_1 \mathbf{v}_1+m_2 \mathbf{v}_2+\ldots+m_n \mathbf{v}_n \dots(7.8)
\end{aligned}
\)
where \(\mathbf{v}_1\left(=\mathrm{d} \mathbf{r}_1 / \mathrm{d} t\right)\) is the velocity of the first particle \(\mathbf{v}_2\left(=d \mathbf{r}_2 / d t\right)\) is the velocity of the second particle etc. and \(\mathbf{V}=\mathrm{d} \mathbf{R} / \mathrm{d} t\) is the velocity of the centre of mass. Note that we assumed the masses \(m_1, m_2, \ldots\), etc. do not change in time. We have, therefore, treated them as constants in differentiating the equations with respect to time.
Differentiating Eq.(7.8) with respect to time, we obtain
\(
\begin{aligned}
& M \frac{\mathrm{d} \mathbf{V}}{\mathrm{d} t}=m_1 \frac{\mathrm{d} \mathbf{v}_1}{\mathrm{~d} t}+m_2 \frac{\mathrm{d} \mathbf{v}_2}{\mathrm{~d} t}+\ldots+m_n \frac{\mathrm{d} \mathbf{v}_n}{\mathrm{~d} t} \\
& \text { or } \\
& M A_{CM}=m_1 \mathbf{a}_1+m_2 \mathbf{a}_2+\ldots+m_n \mathbf{a}_n \dots(7.9)
\end{aligned}
\)
where \(\mathbf{a}_1\left(=d \mathbf{v}_1 / d t\right)\) is the acceleration of the first particle, \(\mathbf{a}_2\left(=\mathrm{d} \mathbf{v}_2 / \mathrm{d} t\right)\) is the acceleration of the second particle etc, and \(\mathbf{A_{CM}}(=\mathrm{dV} / \mathrm{d} t)\) is the acceleration of the centre of mass of the system of particles.

Now, from Newton’s second law, the force acting on the first particle is given by \(\mathbf{F}_1=m_1 \mathbf{a}_1\). The force acting on the second particle is given by \(\mathbf{F}_2=m_2 \mathbf{a}_2\) and so on. Eq. (7.9) may be written as
\(
M \mathbf{A}_{CM}=\mathbf{F}_1+\mathbf{F}_2+\ldots+\mathbf{F}_n \dots(7.10)
\)

Thus, the total mass of a system of particles times the acceleration of its centre of mass is the vector sum of all the forces acting on the system of particles.

Note when we talk of the force \(\mathbf{F}_1\) on the first particle, it is not a single force, but the vector sum of all the forces on the first particle; likewise for the second particle, etc. Among these forces on each particle, there will be external forces exerted by bodies outside the system and also internal forces exerted by the particles on one another. We know from Newton’s third law that these internal forces occur in equal and opposite pairs and in the sum of forces of Eq. (7.10), their contribution is zero. Only the external forces contribute to the equation. We can then rewrite Eq. \((7.10)\) as

\(
M \mathbf{A}_{CM}=\mathbf{F}_{e x t} \dots(7.11)  (M \vec{a}_{C M}=\vec{F}_{e x t})
\)
where \(\mathbf{F}_{e x t}\) represents the sum of all external forces acting on the particles of the system.
Eq. (7.11) states that the centre of mass of a system of particles moves as if all the mass of the system was concentrated at the centre of mass and all the external forces were applied at that point.

If the external forces acting on the system add to zero, \(\vec{a}_{C M}=\mathbf{A}_{CM}=0\), and hence the velocity of the centre of mass is constant. If initially, the centre of mass was at rest with respect to an inertial frame, it will continue to be at rest with respect to that frame. The individual particles may go on complicated paths changing their positions, but the centre of mass will be obtained at the same position.

If the centre of mass was moving with respect to the inertial frame at a speed \(v\) along a particular direction, it will continue its motion along the same straight line with the same speed. Thus, the motion of the centre of mass of the system is not affected by the internal forces. If the external forces add up to zero, the centre of mass has no acceleration.

When the external forces do not add up to zero, the centre of mass is accelerated and the acceleration is given by the equation
\(
\vec{a}_{C M}=\frac{\vec{F}_{e x t}}{M}
\)
If we have a single particle of mass \(M\) on which a force \(\vec{F}_{\text {ext }}\) acts, its acceleration would be the same as \(\frac{\vec{F}_{\text {ext }}}{M}\). Thus the motion of the centre of mass of a system is identical to the motion of a single particle of mass equal to the mass of the given system, acted upon by the same external forces that act on the system.

The centre of mass of the fragments of the projectile

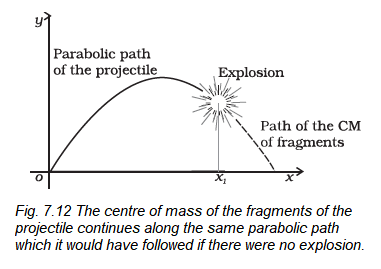
Figure 7.12 is a good illustration of Eq. (7.11). A projectile, following the usual parabolic trajectory, explodes into fragments midway in the air. The forces leading to the explosion are internal forces. They contribute nothing to the motion of the centre of mass. The total external force, namely, the force of gravity acting on the body, is the same before and after the explosion. The centre of mass under the influence of the external force continues, therefore, along the same parabolic trajectory as it would have followed if there were no explosion.