4.10 Projectile motion
PROJECTILE MOTION
When a particle is thrown obliquely near the earth’s surface, it moves along a curved path. Such a particle is called a projectile and its motion is called projectile motion. If we neglect the air resistance the acceleration of a particle is then almost constant. It is in the vertically downward direction and its magnitude is \(g\) which is about \(9.8 \mathrm{~m} / \mathrm{s}^{2}\).
Figure 4n shows a particle projected from the point \(O\) with an initial velocity \(u\) at an angle \(\theta\) with the horizontal. It goes through the highest point \(A\) and falls at \(B\) on the horizontal surface through \(O\). The point \(O\) is called the point of projection, the angle \(\theta\) is called the angle of projection, and the distance \(O B\) is called the horizontal range or simply range. The total time taken by the particle in describing the path \(O A B\) is called the time of flight.
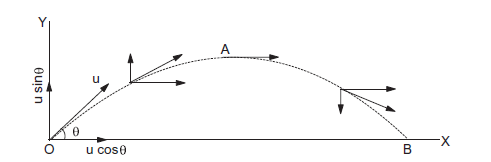 Figure 4n
Figure 4n
The motion of the projectile can be discussed separately for the horizontal and vertical parts. We take the origin at the point of projection. The instant when the particle is projected is taken as \(t=0\). The plane of motion is taken as the \(X-Y\) plane. The horizontal line \(O X\) is taken as the \(X\)-axis and the vertical line \(O Y\) as the \(Y\)-axis. Vertically upward direction is taken as the positive direction of the \(Y\)-axis. After the object has been projected, the acceleration acting on it is due to gravity which is directed vertically downward.
The components of initial velocity \({u}\) and acceleration \({a}\) are:
\(\quad u_{x}=u \cos \theta ; \quad a_{x}=0\\\)\(\quad u_{y}=u \sin \theta ; \quad a_{y}=-g .\)
Horizontal Motion
As \(a_{x}=0\), we have \(v_{x}=u_{x}+a_{x} t=u_{x}=u \cos \theta\)
and \(x=u_{x} t+\frac{1}{2} a_{x} t^{2}=u_{x} t=u t \cos \theta .\)
As indicated in figure 4n, the \(x\)-component of the velocity remains constant as the particle moves.
Vertical Motion
The acceleration of the particle is \(g\) in the downward direction. Thus, \(a_{y}=-g\). The \(y\)-component of the initial velocity is \(u_{y}\). Thus,
\(
\begin{aligned}
v_{y} &=u_{y}-g t = u \sin \theta -g t \\
y &=u_{y} t-\frac{1}{2} g t^{2} .
\end{aligned}
\)
Also we have,
\(
v_{y}^{2}=u_{y}^{2}-2 g y .
\)
The vertical motion is identical to the motion of a particle projected vertically upward with speed \(u \sin \theta\). The horizontal motion of the particle is identical to a particle moving horizontally with uniform velocity \(u \cos \theta\).
Equation of path of a projectile
What is the shape of the path followed by the projectile? This can be seen by eliminating the time between the expressions for \(x\) and \(y\) as given in the two equations below derived earlier.
We obtain: \(
y=\left(\tan \theta\right) x-\frac{g}{2\left(u \cos \theta\right)^{2}} x^{2}
\)
Now, since \(g, \theta\) and \(u\) are constants, above equation is of the form \(y=a x+b x^{2}\), in which \(a\) and \(b\) are constants. This is the equation of a parabola, i.e. the path of the projectile is a parabola.
Time of Flight
In Figure 4n, the particle is projected from the point \(O\) and reaches the same horizontal plane at the point \(B\). The total time taken to reach \(B\) is the time of flight.
Suppose the particle is at \(B\) at a time \(t\). The equation for horizontal motion gives
\(
O B=x=u t \cos \theta
\)
The \(y\)-coordinate at the point \(B\) is zero. Thus, from the equation of vertical motion,
\(
y=u t \sin \theta-\frac{1}{2} g t^{2}
\)
or, \(\quad 0=u t \sin \theta-\frac{1}{2} g t^{2}\)
or, \(\quad t\left(u \sin \theta-\frac{1}{2} g t\right)=0 .\)
Thus, either \(t=0\) or, \(t=\frac{2 u \sin \theta}{g}\).
Now \(t=0\) corresponds to the position \(O\) of the particle. The time at which it reaches \(B\) is thus,
\(
T_{f}=\frac{2 u \sin \theta}{g}
\)
We call \(T_{f}\) the time of flight of the projectile.
Time of maximum height
How much time does the projectile take to reach the maximum height? Let this time be denoted by \(t_{m^{*}}\) Since at this point, \(v_{y}=0\), we have:
\(\quad \begin{aligned} v_{y}=u \sin \theta-g t_{m}=0 \\
\text { Therefore }, t_{m}={u} \sin \theta / g
\end{aligned}
\)
We note that \(T_{f}=2 t_{m}\), which is expected because of the symmetry of the parabolic path.
Maximum height of a projectile
The maximum height \(h_{m}\) reached by the projectile can be calculated by substituting \(t=t_{m}\) in the equation \(y=u t \sin \theta-\frac{1}{2} g t^{2}\).
&=(u \sin \theta)\left(\frac{u \sin \theta}{g}\right)-\frac{1}{2} g\left(\frac{u \sin \theta}{g}\right)^{2} \\
&=\frac{u^{2} \sin ^{2} \theta}{g}-\frac{1}{2} \frac{u^{2} \sin ^{2} \theta}{g} \\
&=\frac{u^{2} \sin ^{2} \theta}{2 g}
\end{aligned}\)
Example 1:
A ball is thrown from a field with a speed of \(12.0 \mathrm{~m} / \mathrm{s}\) at an angle of \(45^{\circ}\) with the horizontal. At what distance will it hit the field again? Take \(g=10.0 \mathrm{~m} / \mathrm{s}^{2}\).
Solution: The horizontal range \(=\frac{u^{2} \sin 2 \theta}{g}\)
\(
\begin{aligned}
&=\frac{(12 \mathrm{~m} / \mathrm{s})^{2} \times \sin \left(2 \times 45^{\circ}\right)}{10 \mathrm{~m} / \mathrm{s}^{2}} \\
&=\frac{144 \mathrm{~m} / \mathrm{s}^{2}}{10.0 \mathrm{~m} / \mathrm{s}^{2}}=14.4 \mathrm{~m} .
\end{aligned}
\)
Thus, the ball hits the field at \(14.4 \mathrm{~m}\) from the point of projection.
Horizontal range of a projectile
The horizontal distance travelled by a projectile from its initial position \((x=y=0)\) to the position where it passes \(y=0\) during its fall is called the horizontal range, \(R\). It is the distance travelled during the time of flight \(T_{f}\). Therefore, the range \(R\) can be calculated (which is the distance \(O B\) as shown in Figure 4n). by using the distance travelled by the particle in time \(T_{f}=\frac{2 u \sin \theta}{g}\) in the equation of horizontal motion as shown below:
\(
\begin{aligned}
x &=(u \cos \theta) t \\
\text { or, } \quad R &=(u \cos \theta) T_{f} =(u \cos \theta)\left(\frac{2 u \sin \theta}{g}\right) \\
&=\frac{2 u^{2} \sin \theta \cos \theta}{g} \\
&=\frac{u^{2} \sin 2 \theta}{g}
\end{aligned}
\)
The range equation R shows that for a given projection velocity \(u, R\) is maximum when \(\sin\) \(2 \theta\) is maximum, i.e., when \(\theta_{0}=45^{\circ}\). The maximum horizontal range is, therefore,
\(
R_{m}=\frac{u^{2}}{g}
\)
Example 2:
A hiker stands on the edge of a cliff \(490 \mathrm{~m}\) above the ground and throws a stone horizontally with an initial speed of \(15 \mathrm{~m} \mathrm{~s}^{-1}\). Neglecting air resistance, find the time taken by the stone to reach the ground, and the speed with which it hits the ground. (Take \(g=9.8 \mathrm{~m} \mathrm{~s}^{-2}\) ).
Solution: We choose the origin of the \(x\)-, and \(y\)– axis at the edge of the cliff and \(t=0 \mathrm{~s}\) at the instant the stone is thrown. Choose the positive direction of \(x\)-axis to be along the initial velocity and the positive direction of \(y\)-axis to be the vertically upward direction. The \(x\)-, and \(y\)– components of the motion can be treated independently. The equations of motion are:
\(x(t)=x_{o}+v_{0 x} t\)
\(y(t)=y_{o}+v_{\text {oy }} t+(1 / 2) a_{y} t^{2}\)
Here, \(x_{0}=y_{0}=0, v_{\text {oy }}=0, a_{y}=-g=-9.8 \mathrm{~m} \mathrm{~s}^{-2}\), \(v_{\mathrm{ox}}=15 \mathrm{~m} \mathrm{~s}^{-1}\).
The stone hits the ground when \(y(t)=-490 \mathrm{~m}\). \(-490 \mathrm{~m}=-(1 / 2)(9.8) t^{2}\).
This gives \(t=10 \mathrm{~s}\).
The velocity components are \(v_{x}=v_{a x}\) and \(v_{y}=v_{o y}-g t\)
so that when the stone hits the ground :
\(
\begin{aligned}
&v_{a x}=15 \mathrm{~m} \mathrm{~s}^{-1} \\
&v_{o y}=0-9.8 \times 10=-98 \mathrm{~m} \mathrm{~s}^{-1}
\end{aligned}
\)
Therefore, the speed of the stone is
\(
\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{15^{2}+98^{2}}=99 \mathrm{~m} \mathrm{~s}^{-1}
\)
Example 3:
A cricket ball is thrown at a speed of \(28 \mathrm{~m} \mathrm{~s}^{-1}\) in a direction \(30^{\circ}\) above the horizontal. Calculate (a) the maximum height, (b) the time taken by the ball to return to the same level, and (c) the distance from the thrower to the point where the ball returns to the same level.
Solution: (a) The maximum height is given by
\(
h_{m}=\frac{\left(u \sin \theta\right)^{2}}{2 g}=\frac{\left(28 \sin 30^{\circ}\right)^{2}}{2(9.8)} \mathrm{m}
\)
\(
=\frac{14 \times 14}{2 \times 9.8}=10.0 \mathrm{~m}
\)
(b) The time taken to return to the same level is
\(
=28 / 9.8 \mathrm{~s}=2.9 \mathrm{~s}
\)
(c) The distance from the thrower to the point where the ball returns to the same level is
\(
R=\frac{\left(u^{2} \sin 2 \theta\right)}{g}=\frac{28 \times 28 \times \sin 60^{\circ}}{9.8}=69 \mathrm{~m}
\)
Example 4: A swimmer can swim in still water at a rate \(4.0 \mathrm{~km} / \mathrm{h}\). If he swims in a river flowing at \(3.0 \mathrm{~km} / \mathrm{h}\) and keeps his direction (with respect to water) perpendicular to the current, find his velocity with respect to the ground.
Answer: The velocity of the swimmer with respect to water is \(\vec{v}_{S, R}=4 \cdot 0 \mathrm{~km} / \mathrm{h}\) in the direction perpendicular to the river. The velocity of river with respect to the ground is \(\vec{v}_{R, G}=3.0 \mathrm{~km} / \mathrm{h}\) along the length of the river. The velocity of the swimmer with respect to the ground is \(\vec{v}_{S, G}\) where
\(
\vec{v}_{S, G}=\vec{v}_{S, R}+\vec{v}_{R, G}
\)
Figure (3.12) shows the velocities. It is clear that,
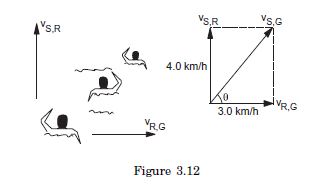
\(
\begin{aligned}
v_{S, G} & =\sqrt{(4 \cdot 0 \mathrm{~km} / \mathrm{h})^2+(3 \cdot 0 \mathrm{~km} / \mathrm{h})^2} \\
& =5 \cdot 0 \mathrm{~km} / \mathrm{h}
\end{aligned}
\)
The angle \(\theta\) made with the direction of flow is
\(
\tan \theta=\frac{4 \cdot 0 \mathrm{~km} / \mathrm{h}}{3 \cdot 0 \mathrm{~km} / \mathrm{h}}=\frac{4}{3} .
\)
Example 5: A man is walking on a level road at a speed of \(3.0 \mathrm{~km} / \mathrm{h}\). Raindrops fall vertically with a speed of \(4.0 \mathrm{~km} / \mathrm{h}\). Find the velocity of the raindrops with respect to the man.
Answer: We have to find the velocity of raindrops with respect to the man. The velocity of the rain as well as the velocity of the man are given with respect to the street. We have
\(
\vec{v}_{\text {rain, man }}=\vec{v}_{\text {rain, street }}-\vec{v}_{\text {man, street }} \text {. }
\)
Figure (3.13) shows the velocities.
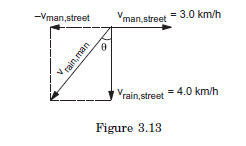
It is clear from the figure that
\(
\begin{aligned}
v_{\text {rain,man }} & =\sqrt{(4 \cdot 0 \mathrm{~km} / \mathrm{h})^2+(3 \cdot 0 \mathrm{~km} / \mathrm{h})^2} \\
& =5 \cdot 0 \mathrm{~km} / \mathrm{h} .
\end{aligned}
\)
The angle with the vertical is \(\theta\), where
\(
\tan \theta=\frac{3.0 \mathrm{~km} / \mathrm{h}}{4 \cdot 0 \mathrm{~km} / \mathrm{h}}=\frac{3}{4} .
\)
Thus, the rain appears to fall at an angle \(\tan ^{-1}(3 / 4)\) with the speed \(5.0 \mathrm{~km} / \mathrm{h}\) as viewed by the man.