4.4 Addition and subtraction of vectors — graphical method

ADDITION OF VECTORS

If \(\vec{a}\) and \(\vec{b}\) are the two vectors to be added, a diagram is drawn in which the tail of \(\vec{b}\) coincides with the head of \(\vec{a}\). The vector joining the tail of \(\vec{a}\) with the head of \(\vec{b}\) is the vector sum of \(\vec{a}\) and \(\vec{b}\). Figure 4a shows the construction. 

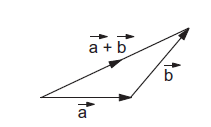figure 4a

If we draw the vectors \(\vec{a}\) and \(\vec{b}\) with both the tails coinciding (shown in figure 4b). Taking these two as the adjacent sides we complete the parallelogram. The diagonal through the common tails gives the sum of the two vectors. Thus, in Figure 4b, \( \overrightarrow{A B}+\overrightarrow{A C}=\overrightarrow{A D}\).

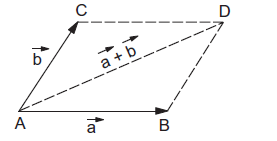figure 4b

Assume that the magnitude of \(\vec{a}=a\) and that of \(\vec{b}=b\). What is the magnitude of \(\vec{a}+\vec{b}\) and what is its direction? Suppose the angle between \(\vec{a}\) and \(\vec{b}\) is \(\theta\).We can see from figure 4c that

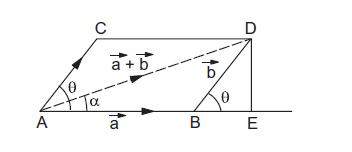figure 4c
\(
\begin{aligned}
A D^{2} &=(A B+B E)^{2}+(D E)^{2} \\
&=(a+b \cos \theta)^{2}+(b \sin \theta)^{2} \\
&=a^{2}+2 a b \cos \theta+b^{2}
\end{aligned}
\)
Thus, the magnitude of \(\vec{a}+\vec{b}\) is
\(
\sqrt{a^{2}+b^{2}+2 a b \cos \theta}
\)
Its angle with \(\vec{a}\) is \(\alpha\) where
\(
\tan \alpha=\frac{D E}{A E}=\frac{b \sin \theta}{a+b \cos \theta} .
\)

Example: 4.0

Rain is falling vertically with a speed of \(35 \mathrm{~m} \mathrm{~s}^{-1}\). Winds start blowing after some time with a speed of \(12 \mathrm{~m} \mathrm{~s}^{-1}\) in the east-to-west direction. In which direction should a boy waiting at a bus stop hold his umbrella?

Solution:

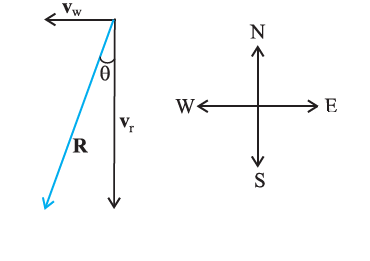figure 4d

The velocity of the rain and the wind are represented by the vectors \(\mathbf{v}_{\mathbf{r}}\) and \(\mathbf{v}_{\mathbf{w}}\) in the above figure 4d and are in the direction specified by the problem. Using the rule of vector addition, we see that the resultant of \(\mathbf{v}_{\mathbf{r}}\) and \(\mathbf{v}_{\mathbf{w}}\) is \(\mathbf{R}\) as shown in the figure. The magnitude of \(\mathbf{R}\) is
\(
R=\sqrt{v_{r}^{2}+v_{w}^{2}}=\sqrt{35^{2}+12^{2}} \mathrm{~m} \mathrm{~s}^{-1}=37 \mathrm{~m} \mathrm{~s}^{-1}
\)
The direction \(\theta\) that \(R\) makes with the vertical is given by
\(
\tan \theta=\frac{v_{w}}{v_{r}}=\frac{12}{35}=0.343
\)
Or, \(\quad \theta=\tan ^{-1}(0.343)=19^{\circ}\)
Therefore, the boy should hold his umbrella in the vertical plane at an angle of about \(19^{\circ}\) with the vertical towards the east.

SUBTRACTION OF VECTORS

Let \(\vec{a}\) and \(\vec{b}\) be two vectors. We define \(\vec{a}-\vec{b}\) as the sum of the vector \(\vec{a}\) and the vector \((-\vec{b})\). To subtract \(\vec{b}\) from \(\vec{a}\), invert the direction of \(\vec{b}\) and add to \(\vec{a}\). The figure below shows the process.

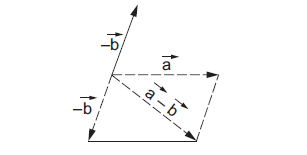figure 4e

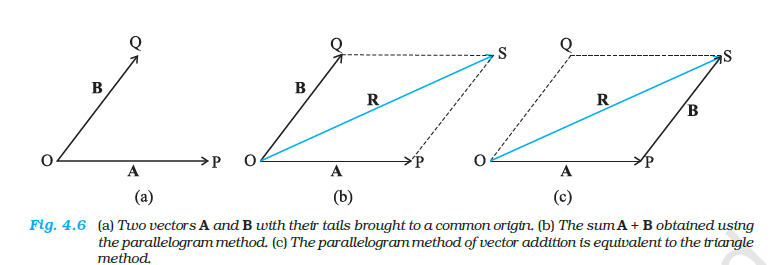
Parallelogram method of vector addition

We can also use the parallelogram method to find the sum of two vectors. Suppose we have two vectors \(\mathbf{A}\) and \(\mathbf{B}\). To add these vectors, we bring their tails to a common origin \(\mathrm{O}\) as shown in Fig. 4.6(a). Then we draw a line from the head of \(\mathbf{A}\) parallel to \(\mathbf{B}\) and another line from the head of B parallel to \(\mathbf{A}\) to complete a parallelogram OQSP. Now we join the point of the intersection of these two lines to the origin \(O\). The resultant vector \(\mathbf{R}\) is directed from the common origin \(\mathrm{O}\) along the diagonal (OS) of the parallelogram [Fig. 4.6(b)]. In Fig.4.6(c), the triangle law is used to obtain the resultant of \(\mathbf{A}\) and \(\mathbf{B}\) and we see that the two methods yield the same result. Thus, the two methods are equivalent.

Example 4.1: Two vectors having equal magnitudes A make an angle \(\theta\) with each other. Find the magnitude and direction of the resultant.

Answer: The magnitude of the resultant will be
\(
\begin{aligned}
B & =\sqrt{A^2+A^2+2 A A \cos \theta} \\
& =\sqrt{2 A^2(1+\cos \theta)}=\sqrt{4 A^2 \cos ^2 \frac{\theta}{2}} \\
& =2 A \cos \frac{\theta}{2} .
\end{aligned}
\)
The resultant will make an angle \(\alpha\) with the first vector where
\(
\tan \alpha=\frac{A \sin \theta}{A+A \cos \theta}=\frac{2 A \sin \frac{\theta}{2} \cos \frac{\theta}{2}}{2 A \cos ^2 \frac{\theta}{2}}=\tan \frac{\theta}{2}
\)
or, \(\quad \alpha=\frac{\theta}{2}\)
Thus, the resultant of two equal vectors bisects the angle between them.

Example 4.2: Two vectors of equal magnitude 5 unit have an angle \(60^{\circ}\) between them. Find the magnitude of (a) the sum of the vectors and (b) the difference of the vectors.

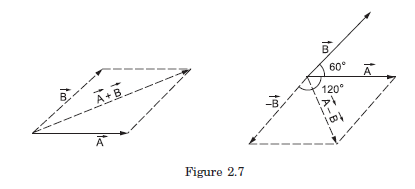
Answer: Figure (2.7) shows the construction of the sum \(\vec{A}+\vec{B}\) and the difference \(\vec{A}-\vec{B}\).
(a) \(\vec{A}+\vec{B}\) is the sum of \(\vec{A}\) and \(\vec{B}\). Both have a magnitude of 5 unit and the angle between them is \(60^{\circ}\). Thus, the magnitude of the sum is
\(
\begin{aligned}
|\vec{A}+\vec{B}| & =\sqrt{5^2+5^2+2 \times 5 \times 5 \cos 60^{\circ}} \\
& =2 \times 5 \cos 30^{\circ}=5 \sqrt{3} \text { unit. }
\end{aligned}
\)
(b) \(\vec{A}-\vec{B}\) is the sum of \(\vec{A}\) and \((-\vec{B})\). As shown in the figure, the angle between \(\vec{A}\) and \((-\vec{B})\) is \(120^{\circ}\). The magnitudes of both \(\vec{A}\) and \((-\vec{B})\) is 5 unit. So,
\(
\begin{aligned}
|\vec{A}-\vec{B}| & =\sqrt{5^2+5^2+2 \times 5 \times 5 \cos 120^{\circ}} \\
& =2 \times 5 \cos 60^{\circ}=5 \text { unit. }
\end{aligned}
\)