3.3 Average velocity and average speed

AVERAGE VELOCITY AND AVERAGE SPEED

Average velocity is defined as the change in position or displacement of the object \((\Delta x)\) divided by the time intervals \((\Delta t)\), in which the displacement occurs:
\(\vec{v}_{a v}=\frac{x_{2}-x_{1}}{t_{2}-t_{1}}=\frac{\Delta x}{\Delta t}\)
where \(x_{2}\) and \(x_{1}\) are the positions of the object at time \(t_{2}\) and \(t_{1}\), respectively. Here the bar over the symbol for velocity is a standard notation used to indicate an average quantity. The SI unit for velocity is \(\mathrm{m} / \mathrm{s}\) or \(\mathrm{m} \mathrm{s}^{-1}\). Like displacement, average velocity is also a vector quantity. 

Average speed is defined as the total the distance travelled by the particle divided by the total time interval during which the motion has taken place:
Average speed \(=\frac{\text { Total path length }}{\text { Total time interval }}\)

The average speed of a particle in a time interval is defined as divided by the time interval. If the particle travels a distance \(s\) in time \(t_{1}\) to \(t_{2}\), the average speed is defined as
\(v_{a v}=\frac{s}{t_{2}-t_{1}}\).

Average speed has the same unit \(\left(\mathrm{m} \mathrm{s}^{-1}\right)\) as that of velocity. It is always positive as it does not tell us in what direction an object is moving (in contrast to the average velocity which can be positive or negative).

INSTANTANEOUS VELOCITY AND SPEED

The instantaneous velocity or velocity is defined as the limit of the average velocity as the time interval \(\Delta t\) becomes infinitesimally small. In other words, 
\(
\begin{aligned}
v &=\lim _{\Delta \mathrm{t} \rightarrow 0} \frac{\Delta x}{\Delta t} \\
&=\frac{\mathrm{d} x}{\mathrm{~d} t}
\end{aligned}
\)
where the symbol \(\lim _{\Delta t \rightarrow 0}\) stands for the operation of taking limit as \(\Delta t \rightarrow 0\) the quantity on its right. In the language of calculus, the quantity \(\frac{\mathrm{d} x}{\mathrm{~d} t}\) is the differential coefficient of \(x\) with respect to \(t\). It is the rate of change of position with respect to time, at that instant.

Example 3.2:

The position of an object moving along \(x\)-axis is given by \(x=a+b t^{2}\) where \(a=8.5 \mathrm{~m}, b=2.5 \mathrm{~m} \mathrm{~s}^{-2}\) and \(t\) is measured in seconds. What is its velocity at \(t=0 \mathrm{~s}\) and \(t=2.0 \mathrm{~s}\). What is the average velocity between \(t=2.0 \mathrm{~s}\) and \(t=4.0 \mathrm{~s}\)?

Answer: In the notation of differential calculus, the velocity is
\(
v=\frac{\mathrm{d} x}{\mathrm{~d} t}=\frac{\mathrm{d}}{\mathrm{d} t}\left(a+b t^{2}\right)=2 b t=5.0 \mathrm{t} \mathrm{m} \mathrm{s}^{-1}\)
At \(t=0 \mathrm{~s}, \quad v=0 \mathrm{~m} \mathrm{~s}^{-1}\) and at \(t=2.0 \mathrm{~s}\), \(v=10 \mathrm{~m} \mathrm{~s}^{-1}\).
\(
\begin{aligned}
\text { Average velocity } &=\frac{x(4.0)-x(2.0)}{4.0-2.0} \\
&=\frac{a+16 b-a-4 b}{2.0}=6.0 \times b \\
&=6.0 \times 2.5=15 \mathrm{~m} \mathrm{~s}^{-1}
\end{aligned}
\)

The instantaneous speed at a time \(t\) is defined as
\(v=\lim _{\Delta t \rightarrow 0} \frac{\Delta s}{\Delta t}=\frac{d s}{d t}\)
where \(s\) is the distance travelled in time \(t\). The average speed is defined for a time interval and the instantaneous speed is defined at a particular instant. Instantaneous speed is also called “speed”.

Example 3.3:

The distance travelled by a particle in time \(t\) is given by \(s=\left(2.5 \mathrm{~m} / \mathrm{s}^{2}\right) t^{2}\). Find (a) the average speed of the particle during the time 0 to \(5.0 \mathrm{~s}\), and (b) the instantaneous speed at \(t=5 \cdot 0 \mathrm{~s}\).

Answer: (a) The distance travelled during time 0 to \(5 \cdot0 \mathrm{~s}\) is
\(
s=\left(2.5 \mathrm{~m} / \mathrm{s}^{2}\right)(5 \cdot 0 \mathrm{~s})^{2}=62.5 \mathrm{~m} .
\)
The average speed during this time is
\(
v_{a v}=\frac{62.5 \mathrm{~m}}{5 \mathrm{~s}}=12.5 \mathrm{~m} / \mathrm{s} .
\)
(b) \(s=\left(2.5 \mathrm{~m} / \mathrm{s}^{2}\right) t^{2}\)
or, \(\quad \frac{d s}{d t}=\left(2.5 \mathrm{~m} / \mathrm{s}^{2}\right)(2 t)=\left(5 \cdot 0 \mathrm{~m} / \mathrm{s}^{2}\right) t\).
At \(t=5 \cdot 0 \mathrm{~s}\) the speed is
\(
v=\frac{d s}{d t}=\left(5 \cdot 0 \mathrm{~m} / \mathrm{s}^{2}\right)(5 \cdot 0 \mathrm{~s})=25 \mathrm{~m} / \mathrm{s}
\)

Example 3.4: Calculate the average velocity of the car between time t = 5 s and t = 7 s shown in Figure 3.4.

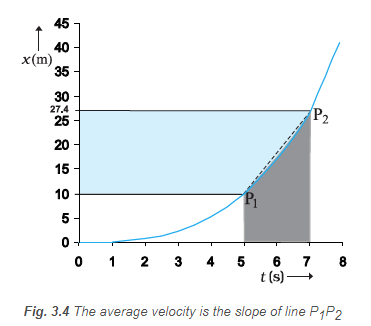
Solution:

\(
v_{ave}=\frac{x_2-x_1}{t_2-t_1}=\frac{(27.4-10.0) \mathrm{m}}{(7-5) \mathrm{s}}=8.7 \mathrm{~m} \mathrm{~s}^{-1}
\)

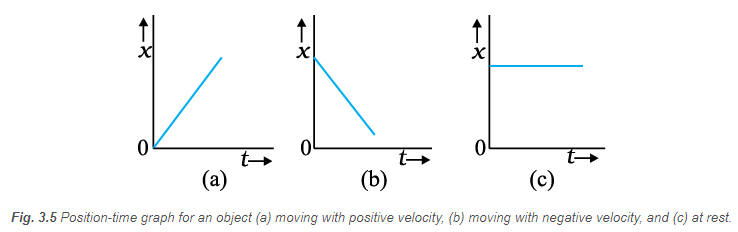
The average velocity can be positive or negative depending upon the sign of the displacement. It is zero if the displacement is zero. Fig. 3.5 shows the \(x\)-t graphs for an object, moving with positive velocity (Fig. 3.5a), moving with negative velocity (Fig. 3.5b) and at rest (Fig. 3.5c).

Example 3.5: A car is moving along a straight line, say OP in Fig. below. It moves from \(O\) to \(P\) in \(18 \mathrm{~s}\) and returns from \(P\) to \(Q\) in \(6.0 \mathrm{~s}\). What are the average velocity and average speed of the car in going (a) from \(\mathrm{O}\) to \(\mathrm{P}\)? and (b) from \(\mathrm{O}\) to \(\mathrm{P}\) and back to \(Q\) ?

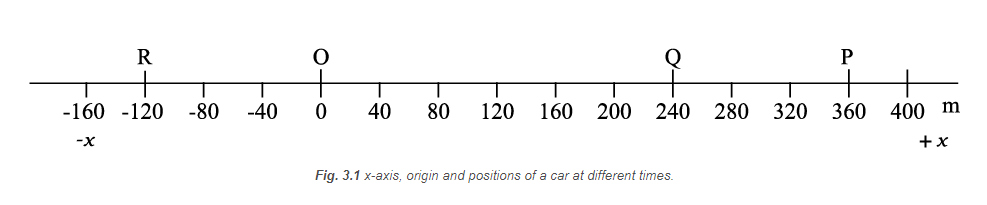
Solution: (a)

\(
\begin{aligned}
& \text { Average velocity }=\frac{\text { Displacement }}{\text { Tume interval }} \\
& \bar{v}=\frac{+360 \mathrm{~m}}{18 \mathrm{~s}}=+20 \mathrm{~m} \mathrm{~s}^{-1} \\
& \text { Average speed }=\frac{\text { Path length }}{\text { Time interval }} \\
& =\frac{360 \mathrm{~m}}{18 \mathrm{~s}}=20 \mathrm{~m} \mathrm{~s}^{-1} \\
&
\end{aligned}
\)

Thus, in this case, the average speed is equal to the magnitude of the average velocity.

(b) In this case,

\(
\begin{aligned}
& \text { Average velocity }=\frac{\text { Displacement }}{\text { Ttme interval }}=\frac{+240 \mathrm{~m}}{(18+6.0) \mathrm{s}} \\
& =+10 \mathrm{~ms}^{-1} \\
& \text { Average speed }=\frac{\text { Path length }}{\text { Ttme interval }}=\frac{\mathrm{OP}+\mathrm{PQ}}{\Delta t} \\
& =\frac{(360+120) \mathrm{m}}{24 \mathrm{~s}}=20 \mathrm{~m} \mathrm{~s}^{-1} \\
&
\end{aligned}
\)
Thus, in this case, the average speed is not equal to the magnitude of the average velocity. This happens because the motion here involves change in direction so that the path length is greater than the magnitude of displacement. This shows that speed is, in general, greater than the magnitude of the velocity.

Example 3.6: The figure below shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time \(t=0\) to \(t=3 \mathrm{~s}\).

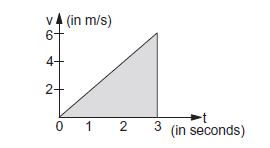
Solution:

The distance travelled by the particle in the time 0 to \(3 \mathrm{~s}\) is equal to the area shaded in the figure. This is a right angled triangle with height \(=6 \mathrm{~m} / \mathrm{s}\) and the base \(=3 \mathrm{~s}\). The area is \(\frac{1}{2}\) (base) (height) \(=\frac{1}{2} \times(3 \mathrm{~s})\) \((6 \mathrm{~m} / \mathrm{s})=9 \mathrm{~m}\). Thus, the particle covered a distance of \(9 \mathrm{~m}\) during the time 0 to \(3 \mathrm{~s}\).

Example 3.7: A table clock has its minute hand \(4.0 \mathrm{~cm}\) long. Find the average velocity of the tip of the minute hand (a) between 6.00 a.m. to 6.30 a.m. and (b) between 6.00 a.m. to 6.30 p.m.

Solution:

At \(6^{\circ} 00\) a.m. the tip of the minute hand is at 12 mark and at 6.30 a.m. or 6.30 p.m. it is \(180^{\circ}\) away. Thus, the straight line distance between the initial and final position of the tip is equal to the diameter of the clock.
Displacement \(=2 R=2 \times 4.0 \mathrm{~cm}=8.0 \mathrm{~cm}\).
The displacement is from the 12 mark to the 6 mark on the clock panel. This is also the direction of the average velocity in both cases.
(a) The time taken from \(6.00 \mathrm{a}. \mathrm{m}\). to \(6.30 \mathrm{~a} . \mathrm{m}\). is 30 minutes \(=1800 \mathrm{~s}\). The average velocity is
\(
v_{a v}=\frac{\text { Displacement }}{\text { time }}=\frac{8.0 \mathrm{~cm}}{1800 \mathrm{~s}}=4 \cdot 4 \times 10^{-3} \mathrm{~cm} / \mathrm{s} \text {. }
\)
(b) The time taken from 6.00 a.m. to 6.30 p.m. is 12 hours and 30 minutes \(=45000 \mathrm{~s}\). The average velocity is
\(
v_{a v}=\frac{\text { Displacement }}{\text { time }}=\frac{8.0 \mathrm{~cm}}{45000 \mathrm{~s}}=1.8 \times 10^{-4} \mathrm{~cm} / \mathrm{s} .
\)