6.9 Summary

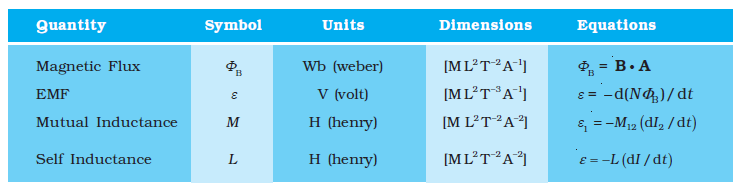
• The magnetic flux through a surface of area \(\mathbf{A}\) placed in a uniform magnetic field \(\mathbf{B}\) is defined as,
  \(
  \Phi_{\mathrm{B}}=\mathbf{B} \cdot \mathbf{A}=B A \cos \theta
  \)
  where \(\theta\) is the angle between \(\mathbf{B}\) and \(\mathbf{A}\).
• Faraday’s laws of induction imply that the emf induced in a coll of \(N\) turns is directly related to the rate of change of flux through it,
  \(
  \varepsilon=-N \frac{\mathrm{~d} \Phi_{\mathrm{B}}}{\mathrm{~d} t}
  \)
  Here \(\Phi_{\mathrm{B}}\) is the flux linked with one turn of the coll. If the circuit is closed, a current \(I=\varepsilon / R\) is set up in it, where \(R\) is the resistance of the circuit.
• Lenz’s law states that the polarity of the induced emf is such that it tends to produce a current which opposes the change in magnetic flux that produces it. The negative sign in the expression for Faraday’s law indicates this fact.
• When a metal rod of length \(l\) is placed normal to a uniform magnetic fleld \(B\) and moved with a velocity \(v\) perpendicular to the fleld, the induced emf (called motional emf) across its ends is
  \(
  \varepsilon=B l v
  \)
• Inductance is the ratio of the flux-linkage to current. It is equal to \(N \Phi / I\).
• A changing current in a coil (coil 2) can induce an emf in a nearby coil (coil 1). This relation is given by,
  \(
  \varepsilon_1=-M_{12} \frac{\mathrm{~d} I_2}{\mathrm{~d} t}
  \)
  The quantity \(M_{12}\) is called mutual inductance of coil 1 with respect to coil 2 . One can similarly define \(M_{21}\). There exists a general equality,
  \(
  M_{12}=M_{21}
  \)
• When a current in a coil changes, it induces a back emf in the same coil. The self-induced emf is glven by,
  \(
  \varepsilon=-L \frac{\mathrm{~d} I}{\mathrm{~d} t}
  \)
  \(L\) is the self-inductance of the coll. It is a measure of the inertia of the coil against the change of current through it.
• The self-inductance of a long solenotd, the core of which consists of a magnetic material of relative permeability \(\mu_{\mathrm{T}}\), is given by
  \(
  L=\mu_r \mu_o n^2 A l
  \)
  where \(A\) is the area of cross-section of the solenold, \(l\) its length and \(n\) the number of turns per unit length.
• In an ac generator, mechanical energy is converted to electrical energy by virtue of electromagnetic induction. If coll of \(N\) turn and area \(A\) is rotated at \(v\) revolutions per second in a uniform magnetic field \(B\), then the motional emf produced is
  \(
  \varepsilon=N B A(2 \pi v) \sin (2 \pi v t)
  \)
  where we have assumed that at time \(t=0 \mathrm{~s}\), the coil is perpendicular to the fleld.

POINTS TO PONDER

• Electricity and magnetism are intimately related. In the early part of the nineteenth century, the experiments of Oersted, Ampere and others established that moving charges (currents) produce a magnetic fleld. Somewhat later, around 1830, the experiments of Faraday and Henry demonstrated that a moving magnet can induce electric current.
• In a closed circuit, electric currents are induced so as to oppose the changing magnetic flux. It is as per the law of conservation of energy. However, in case of an open circuit, an emf is induced across its ends. How is it related to the flux change?
• The motional emf discussed in Section 6.5 can be argued independently from Faraday’s law using the Lorentz force on moving charges. However, even if the charges are stationary land the \(q(\mathbf{v} \times \mathbf{B})\) term of the Lorentz force is not operative], an emf is nevertheless induced in the presence of a time-varying magnetic field. Thus, moving charges in static field and static charges in a time-varying fleld seem to be symmetric situation for Faraday’s law. This gives a tantalising hint on the relevance of the princtple of relativity for Faraday’s law.