Exemplar MCQs
Quiz Summary
0 of 41 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 41 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 41
1. Question
A heavy stone is thrown from a cliff of height h with a speed v. The stone will hit the ground with maximum speed if it is thrown
CorrectIncorrectHint
(d) the speed does not depend on the initial direction.
As the stone falls under the gravitational force, which is a conservative force, the total energy of the stone remains the same at every point during its motion.
From the conservation of energy, we have:
The initial energy of the stone = final energy of the stone
\(
\begin{aligned}
&\text { i.e., }(K . E .)_{i}+(P . E .)_{i}=(K . E .)_{f}+(P . E .)_{f} \\
&\Rightarrow \frac{1}{2} m v^{2}+m g h=\frac{1}{2} m\left(v_{\max }\right)^{2} \\
&\Rightarrow v_{\max }=\sqrt{v^{2}+2 g h}
\end{aligned}
\)
From the above expression, we can say that the maximum speed with which the stone hits the ground does not depend on the initial direction. -
Question 2 of 41
2. Question
Two springs \(A\) and \(B\left(k_{A}=2 k_{B}\right)\) are stretched by applying forces of equal magnitudes at the four ends. If the energy stored in \(A\) is \(E\), that in \(B\) is
CorrectIncorrectHint
(b) Let \(x_{\mathrm{A}}\) and \(x_{\mathrm{B}}\) be the extensions produced in springs \(A\) and \(\mathrm{B}\), respectively.
Restoring force on spring \(A, F=k_{A} x_{A} \quad\)…(i)
Restoring force on spring \(B, F=k_{B} x_{B} \quad\)…(ii)
From (i) and (ii), we get:
\(
k_{A} x_{A}=k_{B} x_{B}
\)
It is given that \(k_{\mathrm{A}}=2 k_{\mathrm{B}}\)
\(
\therefore x_{B}=2 x_{A}
\)
Energy stored in spring \(A: E=\frac{1}{2} k_{A} x_{A}^{2} \quad \ldots\) (iii)
Energy stored in spring \(B: E^{\prime}=\frac{1}{2} k_{B} x_{B}^{2}=\frac{1}{2}\left(\frac{k_{A}}{2}\right)\left(2 x_{A}\right)^{2}\)
\(
\therefore E^{\prime}=2 \times\left(\frac{1}{2} k_{A} x_{A}^{2}\right)=2 E[\text { From }(i i i)]
\) -
Question 3 of 41
3. Question
Two equal masses are attached to the two ends of a spring of spring constant \(k\). The masses are pulled out symmetrically to stretch the spring by a length \(x\) over its natural length. The work done by the spring on each mass is
CorrectIncorrectHint
(d) The work done by the spring on both the masses is equal to the negative of the increase in the elastic potential energy of the spring.
The elastic potential energy of the spring is given by \(E_{p}=\frac{1}{2} k x^{2}\).
Work done by the spring on both the masses \(=-\frac{1}{2} k x^{2}\) (force applied by spring on both the blocks is the same so, work done by spring will be evenly distributed among both the blocks.)
\(\therefore\) Work done by the spring on each mass \(=\frac{1}{2}\left(-\frac{1}{2} k x^{2}\right)=-\frac{1}{4} k x^{2}\) -
Question 4 of 41
4. Question
The negative of the work done by the conservative internal forces on a system equals the change in
CorrectIncorrectHint
(c) Relation between conservative force and potential energy is,
\(
\begin{aligned}
&F=-\mathrm{dU} / \mathrm{dx} \\
&\mathrm{F} \cdot \mathrm{dx}=-\mathrm{dU} \\
&-\mathrm{W}=-\int \mathrm{F} \cdot \mathrm{dx}=\Delta \mathrm{U}
\end{aligned}
\) -
Question 5 of 41
5. Question
The work done by the external forces on a system equals the change in
CorrectIncorrectHint
(a) External forces will either change KE or PE or both of a system. Since total energy (KE+PE) of a system is conserved when no external force acts, hence work done by external force will change total energy.
Work done \(W=\Delta K+\Delta U\)
-
Question 6 of 41
6. Question
The work done by all the forces (external and internal) on a system equals the change in
CorrectIncorrectHint
(b) Though work done by external forces will change the total energy of the system, work done by the internal forces will increase kinetic energy only. So when both do work KE is sure to change.
-
Question 7 of 41
7. Question
_______ of a two-particle system depends only on the separation between the two particles. The most appropriate choice for the blank space in the above sentence is
CorrectIncorrectHint
(c) The potential energy is the quantity which depends only on the separation of the two particles.
The kinetic energy depends on the mass and velocity of the two particles, and hence total energy (which is the sum of kinetic and potential) also depends on these factors. -
Question 8 of 41
8. Question
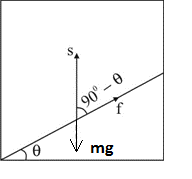
A small block of mass \(m\) is kept on a rough inclined surface of inclination \(\theta\) fixed in an elevator. The elevator goes up with a uniform velocity \(v\) and the block does not slide on the wedge. The work done by the force of friction on the block in time \(t\) will be
CorrectIncorrectHint
(c) As block does not side, Hence, the force of friction.
\(
f=m g \sin \theta
\)
In time \(t\), displacement, \(s v t\)
\(
\therefore W_{f}=f \cdot s \cdot \cos \left(90^{\circ}-\theta\right)=\mu m g \sin \theta \cdot v t \cdot \sin \theta=\mu m g v t \sin ^{2} \theta
\)
-
Question 9 of 41
9. Question
A block of mass m slides down a smooth vertical circular track. During the motion, the block is in
CorrectIncorrectHint
(d) The net force on the block is not zero, therefore the block will not be in any given equilibrium.
-
Question 10 of 41
10. Question
A particle is rotated in a vertical circle by connecting it to a string of length \(l\) and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
CorrectIncorrectHint
(c) Let speed at the top \(=v\), it is balanced by weight \(m g\), so, \(\mathrm{mv}^{2} / \mathrm{l}=\mathrm{mg}\)
\(\rightarrow \mathrm{v}^{2}=\mathrm{gl}\)
Now let the speed when string is horizontal \(=v^{\prime}\)
Here total energy \(=1 / 2 m v^{\prime 2}=1 / 2 m v^{2}+m g l\)
\(v^{\prime 2}=v^{2}+2 g l=g l+2 g l=3 g l\)
\(v^{\prime}=\sqrt{(3 g l)}\) -
Question 11 of 41
11. Question
A heavy stone is thrown from a cliff of height h in a given direction. The speed with which it hits the ground
CorrectIncorrectHint
(a) & (b)
The speed with which it hits the ground must depend upon the speed of projection and shall always be larger than the speed of projection because the potential energy of the body shall be converted into kinetic energy.
-
Question 12 of 41
12. Question
The total work done on a particle is equal to the change in its kinetic energy
CorrectIncorrectHint
(a) According to the work-energy theorem ” The total work done on a system is equal to the change in its kinetic energy”. The given statement is applicable in all systems.
-
Question 13 of 41
13. Question
A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
CorrectIncorrectHint
(c) & (d)
Power \(P=\vec{F} \cdot \vec{v}=F v \cos \theta\). since \(\theta=90^{\circ}, P=0\) i.e. \(\frac{d W}{d t}=0\). Hence the work done by the force is constant. Therefore, kinetic energy of the particle remains constant.
When the force is perpendicular to the velocity and constant in magnitude, then the force acts as a centripetal force, and the body moves in a circular path.
-
Question 14 of 41
14. Question
Consider two observers moving with respect to each other at a speed \(v\) along a straight line. They observe a block of mass \(m\) moving a distance \(l\) on a rough surface. The following quantities will be the same as observed by the two observers
CorrectIncorrectHint
(d) Acceleration is the rate of change of velocity. Though for both observers velocities are different but the difference of velocities are the same, which means the rate of change of velocities (acceleration) is the same.
-
Question 15 of 41
15. Question
You lift a suitcase from the floor and keep it on a table. The work done by you on the suitcase does not depend on
CorrectIncorrectHint
(a), (b) & (d)
Since the force applied by me is a conservative force, the work done by me on the suitcase does not depend on the path taken by the suitcase. (a).
Work done is the product of force and displacement. It does not depend on time. (b).
It does not depend on my weight because we are calculating work done by me on the suitcase. (d).
But it depends on the weight of the suitcase. So (c) is not correct. -
Question 16 of 41
16. Question
No work is done by a force on an object if
CorrectIncorrectHint
(a), (c) & (d)
Since there is no displacement along the force when it is perpendicular to the velocity of an object, so no work is done. Answer (a). (b) is not true because acceleration will always be in the direction of force according to Newton’s Second Law of Motion. No work is done if there is no displacement of the object in the direction of the force. Answer (c). Again there is no displacement along the force, no work done. Answer (d)
-
Question 17 of 41
17. Question
A particle of mass \(m\) is attached to a light string of length \(l\), the other end of which is fixed. Initially, the string is kept horizontal and the particle is given an upward velocity \(v\). The particle is just able to complete a circle.
CorrectIncorrectHint
(a) & (d)
The string becomes slack when the particle reaches its highest point. This is because at the highest point, the tension in the string is minimum. At this point, the potential energy of the particle is maximum, while its kinetic energy is minimum. From the law of conservation of energy, we can see that the particle again passes through the initial position where its potential energy is minimum and its kinetic energy is maximum.
-
Question 18 of 41
18. Question
The kinetic energy of a particle continuously increases with time.
CorrectIncorrectHint
(b) & (d)
The kinetic energy of a particle is directly proportional to the square of its velocity. The resultant force on the particle must be at an angle less than \(90^{\circ}\) with the velocity all the time so that the velocity or kinetic energy of the particle keeps on increasing. The kinetic energy is also directly proportional to the square of its momentum, therefore it continuously increases with the increase in momentum of the particle.
-
Question 19 of 41
19. Question
One end of a light spring of spring constant \(k\) is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work done by the spring is \(\frac{1}{2} k x^{2}\). The possible cases are
CorrectIncorrectHint
(a) & (b)
Since in the conditions of (c) and (d) spring does not exert a force that is in the direction of displacement but in the opposite, so the work done will be negative. Only in (a) and (b) the work done will be positive.
-
Question 20 of 41
20. Question
A block of mass \(M\) is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force \(F\). The kinetic energy of the block increases by \(20 \mathrm{~J}\) in \(1 \mathrm{~s}\).
CorrectIncorrectHint
(b) Tension in the string is equal to F, as tension on both sides of a frictionless and massless pulley is the same.
i.e., \(\mathrm{T}-\mathrm{Mg}=\mathrm{Ma} \Rightarrow \mathrm{T}=\mathrm{Mg}+\mathrm{Ma}\)
So, the tension in the string cannot be equal to \(\mathrm{Mg}\).
The change in kinetic energy of the block is equal to the work done by gravity.
Hence, the work done by gravity is \(20 \mathrm{~J}\) in \(1 \mathrm{~s}\), while the work done by the tension force is zero. -
Question 21 of 41
21. Question
An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is because,
CorrectIncorrectHint
Key concept: To calculate the change in kinetic energy of the system during motion we have to apply work-energy, theorem. According to this theorem, Net work done = Final kinetic energy – Initial kinetic energy of the object The above statement shows the connection between work and kinetic energy as: “The work done by the net force acting on an object is equal to the change in the kinetic energy of that object”.
Net work done on a particle equals the change in the kinetic energy of the particle.
\(
\Sigma W=K_2-K_1
\)
According to the problem as the electron and proton are moving under the influence of mutual forces, the magnetic forces will be perpendicular to their motion, hence, it acts as a centripetal force for the particle. In this way the particle performs the uniform circular motion, this implies speed will remain constant. So, there is no change in the kinetic energy of the particle. Hence no work is done by these forces.
\(
\overrightarrow{F_m}=q(\vec{v} \times \vec{B}) \cdot F_m
\)
(magnetic force) will be perpendicular to both \(B\) and \(v\), where \(B\) is the external magnetic field and \(v\) is the velocity of particle. That is why one ignores the magnetic force of one particle on another. -
Question 22 of 41
22. Question
A proton is kept at rest. A positively charged particle is released from rest at a distance \(d\) in its field. Consider two experiments; one in which the charged particle is also a proton and in another, a positron. In the same time \(t\), the work done on the two moving charged particles is
CorrectIncorrectHint
(c) Force between two protons is equal to the force between proton and a
positron because their charges are same. As the mass of positron is much lesser than proton, (1/1840 times) it moves away through much larger distance compared to proton.
Change in their momentum will be same. So, the velocity of lighter particle will be greater than that of a heavier particle. So, the positron is moved through a larger distance.
As work done \(=\) force \(\times\) distance. As forces are the same in the case of proton and positron but the distance moved by positron is larger, hence, work done will be more. -
Question 23 of 41
23. Question
A man squatting on the ground gets straight up and stands. The force of reaction of the ground on the man during the process is
CorrectIncorrectHint
(d) In the process of squatting on the ground he gets straight up and stand. Then he is tilted somewhat, the man exerts a variable force on the ground to balance his weight, hence he also has to balance frictional force besides his weight in this case.
\(N=\) Normal reaction force \(=\) friction \(+m g=N>m g\)
Once the man gets straight up that variable force \(=0 \Rightarrow\)
Normal reaction force \(=\mathrm{mg}\) -
Question 24 of 41
24. Question
A bicyclist comes to a skidding stop in \(10 \mathrm{~m}\). During this process, the force on the bicycle due to the road is \(200 \mathrm{~N}\) and is directly opposed to the motion. The work done by the cycle on the road is
CorrectIncorrectHint
(c) As friction is present in fhis problem, so mechanical energy is not conserved. So energy will be lost due to dissipation by friction. Here work is done by the frictional force on the cycle and is equal to \(200 \times 10=-2000 \mathrm{~J}\)
As the road does not move at all, therefore, work done by the cycle on the road is zero.
Important point: We should be aware that here the energy of bicyclist is lost during the motion, but it is lost due to friction in the form of heat. -
Question 25 of 41
25. Question
A body is falling freely under the action of gravity alone in a vacuum. Which of the following quantities remain constant during the fall?
CorrectIncorrectHint
(c) As the body is falling freely under gravity, the potential energy decreases continuously and kinetic energy increases continuously as all the conservative forces are doing work. So, total mechanical energy \((\mathrm{PE}+\mathrm{KE})\) of the body will be constant.
Let us discuss this in detail:
In the given diagram an object is dropped from-a height \(\mathrm{H}\) from ground.
At point A total mechanical energy will be \(E A=K . E+P . E\)
\(
E_A=\frac{1}{2} m v^2+m g H
\)
As velocity will be zero at \(A\), so its kinetic energy will be zero.
\(
E_A=m g H
\)
Velocity at point \(B\) will be, \(v_B=\sqrt{2 g h}\)
So energy at point \(B\) will be \(E_B=\mathrm{KE}+\mathrm{PE}\)
\(
\begin{aligned}
E_B & =\frac{1}{2} m(2 g h)+m g(H-h) \\
E_B & =m g h+m g H-m g h \\
E_B & =m g H
\end{aligned}
\)
Now, velocity at point \(C\) will be \(v_c=\sqrt{2 g h}\)
So, energy at point \(C\) will be \(E_C=\mathrm{KE}+\mathrm{PE}\)
\(
\begin{aligned}
E_C & =\frac{1}{2} m(2 g H)+m g(0) \\
E_C & =m g H
\end{aligned}
\)
So, total mechanical energy will remain the same (if we neglect the air friction). -
Question 26 of 41
26. Question
During an inelastic collision between two bodies, which of the following quantities always remain conserved?
CorrectIncorrectHint
(c) If in a collision kinetic energy after collision is not equal to kinetic energy before collision, the collision is said to inelastic.
Coefficient of restitution \(0<e<1\)
When we are considering the two bodies as system the total external force on the system will be zero.
Hence, total linear momentum of the system remain conserved.
Here kinetic energy appears in other forms, i.e. energy may be lost in the form of heat and sound etc. In some cases
\((K E)_{\text {final }}<(K E)_{\text {initial }}\) such as when initial \(K E\) is converted into intertial energy of the product (as heat, elastic or excitation) while in other cases \((\mathrm{KE})_{\text {final }}>(\mathrm{KE})_{\text {initial }}\) such as when internal energy stored in the colliding particles is released.
Examples; (1) Collision between two billiard balls.
(2) Collision between two automobiles on a road.
In fact all majority of collisions belong to this category. -
Question 27 of 41
27. Question
Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track as shown in Fig. 6.1.
Which of the following statement is correct?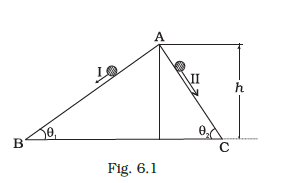 CorrectIncorrect
CorrectIncorrectHint
(c) As shown in diagram \(A B\) and \(A C\) are two smooth planes inclined to the angle \(\theta_1\) and \(\theta_2\) respectively. As friction is absent here, hence, mechanical energy will be conserved. As both the tracks having common height \(h\),
From conservation of mechanical energy,\(
\begin{aligned}
& \frac{1}{2} m v^2=m g h \quad \text { (for both tracks I and II) } \\
& v=\sqrt{2 g h}
\end{aligned}
\)
Hence, speed is same for both stones. For stone \(I, a_1=\) acceleration along inclined plane \(=g \sin \theta_1\)
Similarly, for stone II, \(a_2=g \sin \theta_2\) as \(\theta_2>\theta_1\) hence, \(a_2>a_1\).
And both lengths for track II is also less, hence stone II reaches earlier than the stone I.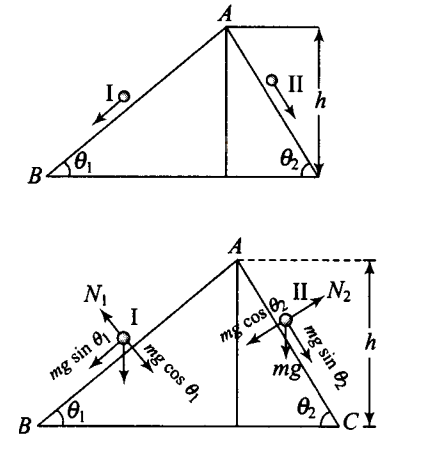
-
Question 28 of 41
28. Question
The potential energy function for a particle executing linear SHM is given by \(V(x)=\frac{1}{2} k x^2\) where \(k\) is the force constant of the oscillator (Fig. 6.2). For \(k=0.5 \mathrm{~N} / \mathrm{m}\), the graph of \(V(x)\) versus \(x\) is shown in the figure. A particle of total energy \(E\) turns back when it reaches \(x= \pm x_m\). If \(V\) and \(K\) indicate the P.E. and K.E., respectively of the particle at \(x=+x_m\), then which of the following is correct?
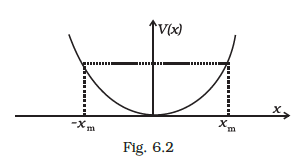 CorrectIncorrect
CorrectIncorrectHint
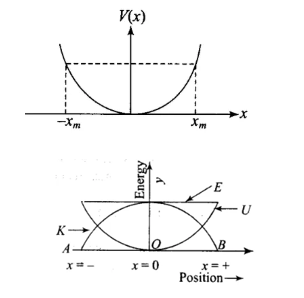
The answer is the option (b) \(V=E, K=O\)
The potential energy at any position,
\(
U=\frac{1}{2} k x^2
\)
Total energy of the mass,
\(
E=\frac{1}{2} k a^2
\)
Kinetic energy at any position,
\(
\begin{aligned}
K & =E-U=\frac{1}{2} k a^2+\frac{1}{2} k x^2 \\
K & =\frac{1}{2} k\left[a^2-x^2\right]
\end{aligned}
\)
Now,
\(
U_{\max }=\frac{1}{2} k a^2 \text { at extremes. }
\)
\(
U_{\min} =0\{\mathrm{x}=0 \text { at mean }\}
\)
\(
K_{\max }=\frac{1}{2} k a^2 \{x=0 \text { at mean }\}
\)
\(K_{\min}=0 \text { \{extremes }\}
\)
\(
\text { Hence, } E=\frac{1}{2} k a^2 \text { is constant at all times }
\)
\(
\text { When particle is at } x=x m \text { (mean), } K E=0
\)
\(
\text { So, total energy is } E=P E+0=\frac{1}{2} k x^2
\)
So, option b is correct. -
Question 29 of 41
29. Question
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed \(V\) as shown in Fig. 6.3.

If the collision is elastic, which of the following (Fig. 6.4) is a possible result after collision?
 CorrectIncorrect
CorrectIncorrectHint
(b)
Key concept: In a collision if the motion of colliding particles before and after the collision is along the same line, the collision is said to be head on or one dimensional.
When two bodies of equal masses collides elastically, their velocities are interchanged.
Kinetic energy and linear momentum remains conserved Total kinetic energy of the system before collision
\(
=\frac{1}{2} m v^2+0=\frac{1}{2} m v^2
\)
In (a), kinetic energy of the system after collision.
\(
K_1=\frac{1}{2}(2 m)\left(\frac{v}{2}\right)^2=\frac{1}{4} m v^2
\)
Hence this option is incorrect.
In (b), kinetic energy of the system after collision,
\(
K_2=\frac{1}{2}(m)(v)^2=\frac{1}{2} m v^2
\)
Hence this option will be correct.
In (c), kinetic energy of the system after collision.
\(
K_3=\frac{1}{2}(3 m)\left(\frac{v}{3}\right)^2=\frac{1}{6} m v^2
\)
Hence this option is incorrect.
In (d), kinetic energy of the system after collision,
\(
K_4=\frac{1}{2} m v^2+\frac{1}{2} m\left(\frac{v}{2}\right)^2+\frac{1}{2} m\left(\frac{v}{3}\right)^2=\frac{49}{72} m v^2
\)
We see that kinetic energy is conserved only in (b). -
Question 30 of 41
30. Question
A body of mass \(0.5 \mathrm{~kg}\) travels in a straight line with velocity \(v=a\) \(x^{3 / 2}\) where \(a=5 \mathrm{~m}^{-1 / 2} \mathrm{~s}^{-1}\). The work done by the net force during its displacement from \(x=0\) to \(x=2 \mathrm{~m}\) is
CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{m}=0.5 \mathrm{~kg} \\
& v=a x^{\frac{3}{2}} \\
& a=5 m^{\frac{-1}{2}} s^{-1}
\end{aligned}
\)
\(=a=\frac{d v}{d t}=v \frac{d v}{d x}\)
\(
=a x^{\frac{3}{2}} \frac{d}{d x} a x^{\frac{3}{2}}=a x^{\frac{3}{2}} \times \frac{3}{2} \times a x^{\frac{1}{2}}=\frac{3}{2} a^2 x^2
\)
Net force \(=m a=m\left(\frac{3}{2} a^2 x^2\right)\)
Work done under the variable force
\(
\begin{aligned}
& =\int_{x=0}^{x=2} F \cdot d x=\int_0^2 \frac{3}{2} m a^2 x^2 d x \\
& =\frac{1}{2} m a^2 \times 8=\frac{1}{2} \times(0.5) \times(25) \times 8=50 J
\end{aligned}
\) -
Question 31 of 41
31. Question
A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in Fig. 6.5 correctly shows the displacement-time curve for its motion?
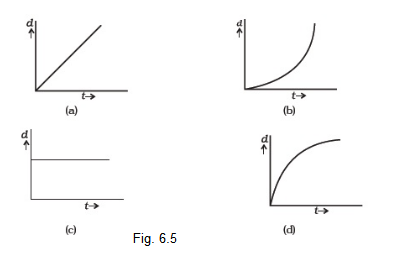 CorrectIncorrect
CorrectIncorrectHint
(b) For constant power
Displacement \(\propto t^{3 / 2}\)
Because
\(
P=\frac{\vec{F} \cdot d \vec{s}}{d t}=\vec{F} \cdot \vec{v}=\text { constant }
\)
( \(\because P=\) constant according to the problem)
Now, will by dimensional analysis
\(
\begin{aligned}
& {[F][v]=\text { constant } } \\
\Rightarrow & {\left[M L T^{-2}\right]\left[L T^{-1}\right]=\text { constant } } \\
\Rightarrow & L^2 T^{-3}=\text { constant } \quad(\because \text { mass is constant }) \\
\Rightarrow & L \propto T^{3 / 2} \Rightarrow \text { Displacement }(d) \propto t^{3 / 2}
\end{aligned}
\) -
Question 32 of 41
32. Question
Which of the diagrams shown in Fig. 6.6 most closely shows the variation in kinetic energy of the earth as it moves once around the sun in its elliptical orbit?
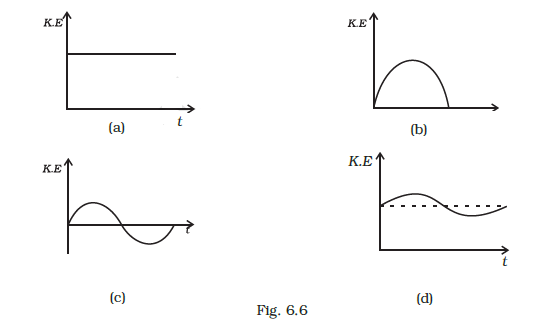 CorrectIncorrect
CorrectIncorrectHint
(d) As the earth moves once around the sun in its elliptical orbit, when the earth is closest to the sun, speed of the earth is maximum, hence KE is maximum. When the earth is farthest from the sun speed is minimum, hence \(K E\) is minimum but never zero and negative. This variation of KE vs t is correctly represented by option (d).
-
Question 33 of 41
33. Question
Which of the diagrams shown in Fig. 6.7 represents the variation of total mechanical energy of a pendulum oscillating in air as a function of time?
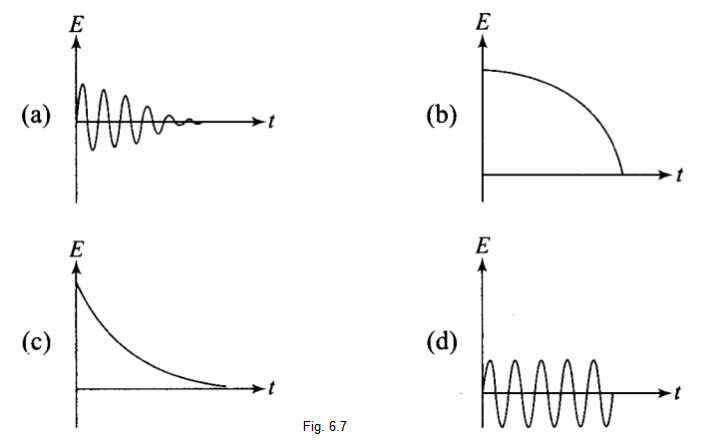 CorrectIncorrect
CorrectIncorrectHint
(c) When a pendulum oscillates in air, its total mechanical energy decreases continuously in overcoming resistance due to air. Therefore, total mechanical energy of the pendulum decreases exponentially with time.
The variation of \(\mathrm{E}\) vs \(\mathrm{t}\) is correctly represented by curve (c) in which the relation between energy and time is shown. -
Question 34 of 41
34. Question
A mass of \(5 \mathrm{~kg}\) is moving along a circular path of radius \(1 \mathrm{~m}\). If the mass moves with 300 revolutions per minute, its kinetic energy would be
CorrectIncorrectHint
(a) According to the problem, Radius \(=1 \mathrm{~m}\), mass \(=m=5 \mathrm{~kg}\) Frequency of revolution, \(f=300 \mathrm{rev} / \mathrm{min}\)
\(
f=\frac{300}{60}
\)
Angular velocity will be
\(
\begin{aligned}
& =2 \pi f=(300 \times 2 \pi) \mathrm{rad} / \mathrm{min} \\
& =(300 \times 2 \times 3.14) \mathrm{rad} / 60 \mathrm{~s} \\
& =\frac{300 \times 2 \times 3.14}{60} \mathrm{rad} / \mathrm{s}=10 \pi \mathrm{rad} / \mathrm{s}
\end{aligned}
\)
And relation between linear velocity and angular velocity is, \(v=\omega R\)
\(
\begin{aligned}
& =\left(\frac{300 \times 2 \pi}{60}\right)(1 \mathrm{~m}) \\
& =10 \pi \mathrm{m} / \mathrm{s}
\end{aligned}
\)
\(
\begin{aligned}
\text { And kinetic energy } & =\frac{1}{2} m v^2 \\
& =\frac{1}{2} \times 5 \times(10 \pi)^2 \Rightarrow 100 \pi^2 \times 5 \times \frac{1}{2} \\
& =250 \pi^2 \mathrm{~J}
\end{aligned}
\) -
Question 35 of 41
35. Question
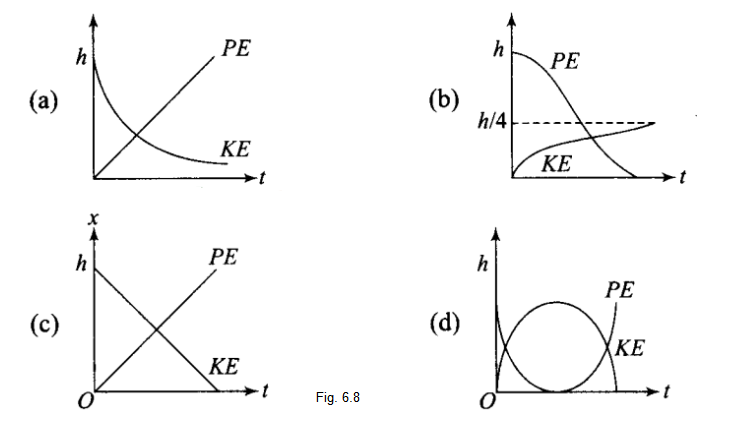
A raindrop falling from a height \(h\) above ground, attains a near terminal velocity when it has fallen through a height \((3 / 4) h\). Which of the diagrams shown in Fig. 6.8 correctly shows the change in kinetic and potential energy of the drop during its fall up to the ground?
 CorrectIncorrect
CorrectIncorrectHint
(b) At height \(h\) from ground raindrop have maximum potential energy. And kinetic velocity will be zero (at the instant when it dropped its velocity will be zero), then as the rain drop falls its PE starts decreasing and kinetic energy start increasing.
The total mechanical energy will remain conserved if we neglect the air resistance. If there is some air resistance, there is some force called upthrust (in fluids) which opposes its motion. It depends upon the velocity of the object as the velocity increases, upthrust also increases. Hence during fall of a raindrop first its velocity increases and then becomes constant after some time.
This constant velocity is called terminal velocity, hence \(K E\) also becomes constant. PE decreases continuously as the drop is falling continuously.
The variation in \(\mathrm{PE}\) and \(\mathrm{KE}\) is best represented by (b). -
Question 36 of 41
36. Question
In a shotput event an athlete throws the shotput of mass \(10 \mathrm{~kg}\) with an initial speed of \(1 \mathrm{~m} \mathrm{~s}^{-1}\) at \(45^{\circ}\) from a height \(1.5 \mathrm{~m}\) above ground. Assuming air resistance to be negligible and acceleration due to gravity to be \(10 \mathrm{~m} \mathrm{~s}^{-2}\), the kinetic energy of the shotput when it just reaches the ground will be
CorrectIncorrectHint
(d) If air resistance is negligible, total mechanical energy of the system will remain constant. And let us take ground as a reference where potential energy will be zero.
According to the problem, \(h=1.5 \mathrm{~m}, v=1 \mathrm{~m} / \mathrm{s}, \mathrm{m}=10 \mathrm{~kg}, \mathrm{~g}=10 \mathrm{~ms}^{-2}\)
\(
\begin{aligned}
\text { Initial energy of the shotput } & =(\mathrm{PE})_i+(\mathrm{KE})_i=m g h+\frac{1}{2} m v^2 \\
& =10 \times 10 \times 1.5+\frac{1}{2} \times 10 \times(1)^2 \\
& =150+5=155 \mathrm{~J}
\end{aligned}
\)
From conservation of mechanical energy,
\(
\begin{aligned}
&(\mathrm{PE})_i+(\mathrm{KE})_i=(\mathrm{PE})_f+(\mathrm{KE})_f \\
& \Rightarrow \quad 155 \mathrm{~J}=0+(\mathrm{KE})_f
\end{aligned}
\)
So, the final kinetic energy of the shotput is \(155 \mathrm{~J}\). -
Question 37 of 41
37. Question
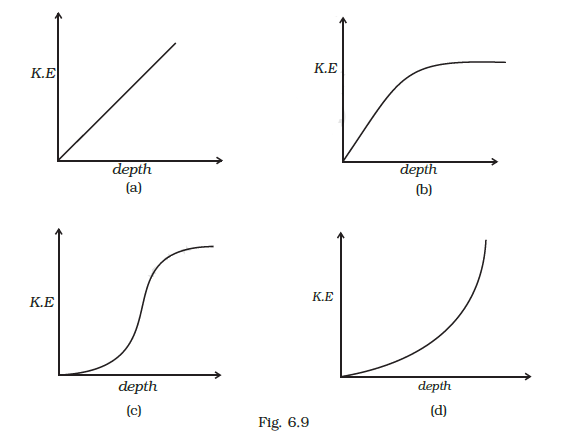
Which of the diagrams in Fig. 6.9 correctly shows the change in kinetic energy of an iron sphere falling freely in a lake having sufficient depth to impart it a terminal velocity?
 CorrectIncorrect
CorrectIncorrectHint
When an iron sphere is falling freely in the lake, it will accelerate first then its velocity increases and resistance due to water causes a viscous force which opposes its motion. Hence, during the fall of the sphere, first its velocity increases and then become constant after some time. option (b) is the best representable graph of it.
-
Question 38 of 41
38. Question
A cricket ball of mass \(150 \mathrm{~g}\) moving with a speed of \(126 \mathrm{~km} / \mathrm{h}\) hits at the middle of the bat, held firmly at its position by the batsman. The ball moves straight back to the bowler after hitting the bat. Assuming that collision between ball and bat is completely elastic and the two remain in contact for \(0.001 \mathrm{~s}\), the force that the batsman had to apply to hold the bat firmly at its place would be
CorrectIncorrectHint
The answer is the option (c)
\(
\begin{aligned}
& m=150 \mathrm{~g}=\frac{150}{1000}=\frac{3}{20} \mathrm{~kg}, t=0.001 \mathrm{~s} \\
& \mathrm{u}=126 \mathrm{~km} / \mathrm{h}=35 \mathrm{~m} / \mathrm{s} \\
& \mathrm{v}=-126 \mathrm{~km} / \mathrm{h}=-35 \mathrm{~m} / \mathrm{s}
\end{aligned}
\)
change in momentum \(=m(v-u)=\frac{3}{20}(-70)=\frac{-21}{2}\)
Force
\(
=\frac{\frac{-21}{2}}{0.001}=-1.05 \times 10^4 \mathrm{~N}
\)
The negative sign indicates the opposite direction of the force. Hence the force exerted by the batman should be \(1.05 \times 10^4 \mathrm{~N}\). -
Question 39 of 41
39. Question
A man, of mass \(m\), standing at the bottom of the staircase, of height \(L\) climbs it and stands at its top.
CorrectIncorrectHint
\((b, d)\) When a man of mass \(m\) climbs up the staircase of height \(L\), work done by the gravitational force on the \(\operatorname{man}=-\mathrm{mgL}\)
Work done by internal muscular forces \(=-\) Work done against gravitational force \(=\mathrm{mg} \mathrm{L}\)
Work done by all the forces \(=\mathrm{mgL}-\mathrm{mgL}=0\)
As the point of application of the contact forces does not move, hence work done by reaction forces will also be zero.
And work done by friction will also be zero as there a no dissipation or rubbing is involved. -
Question 40 of 41
40. Question
A bullet of mass \(m\) fired at \(30^{\circ}\) to the horizontal leaves the barrel of the gun with a velocity \(v\). The bullet hits a soft target at a height \(h\) above the ground while it is moving downward and emerges out with half the kinetic energy it had before hitting the target.
Which of the following statements are correct in respect of the bullet after it emerges out of the target?
CorrectIncorrectHint
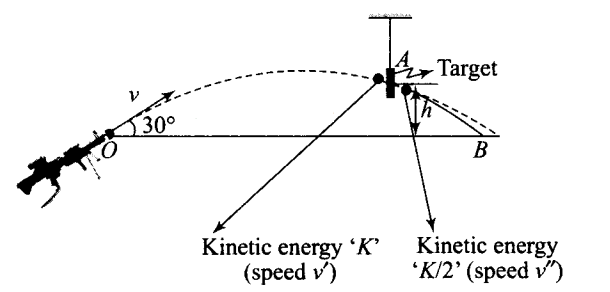
\((b, d, f)\) The given situation is shown in the diagram. Let speed after emerging from the target is \(v^{\prime \prime}, v^{\prime}\) is speed of the bullet just before hitting the target, \(v\) is the initial speed of bullet
(a) The velocity of the bullet after it emerges out of the target will be reduced to half its initial value.
Compare the kinetic energies before and after hitting the target. Just before hitting the target the mechanical energy will be conserved. After hitting its energy will be loose. So by conservation of mechanical energy between ” \(\mathrm{O}\) ” and ” \(\mathrm{A}\) ” ( \(\mathrm{A}\) is the point where the target is placed),
\(
\begin{aligned}
& U_i+K_i=U_f+K_f \\
\Rightarrow & 0+\frac{1}{2} m v^2=m g h+\frac{1}{2} m v^{\prime 2} \\
\Rightarrow & \frac{\left(v^{\prime}\right)^2}{2}=\frac{v^2}{2}=-g h \\
\Rightarrow \quad & \left(v^{\prime}\right)^2=v^2-2 g h \\
\Rightarrow & v^{\prime}=\sqrt{v^2-2 g h} \dots(i)
\end{aligned}
\)
Then,
\(
\begin{aligned}
& =\frac{1}{2}\left(m v^{\prime \prime}\right)^2=\frac{1}{2}\left[\frac{1}{2} m\left(v^{\prime}\right)^2\right] \\
& \frac{1}{2} m\left(v^{\prime \prime}\right)^2=\frac{1}{4} m\left(v^{\prime}\right)^2=\frac{1}{4} m\left[v^2-2 g h\right] \\
\Rightarrow & \left(v^{\prime \prime}\right)^2=\frac{v^2-2 g h}{2}=\frac{v^2}{2}-g h \\
\Rightarrow & v^{\prime \prime}=\sqrt{\frac{v^2}{2}-g h} \dots(ii)
\end{aligned}
\)
If we assume \(K E_1\) and \(K E_2\) to be the kinetic energy of the bullet pre and post target then,
\(
\begin{aligned}
& K E_2=\frac{1}{2} K E_1 \\
& \frac{1}{2} M V_2^2=\frac{1}{4} M V_1^2 \\
& V_2^2=\left(\frac{V_1}{\sqrt{2}}\right)^2=0.707 V_1 \\
& \text { b) } V_2=0.707 V_1
\end{aligned}
\)
Hence, after emerging from the target velocity of the bullet ( \(\left.v^{\prime \prime}\right)\) is more than half of its earlier velocity \(v^{\prime}\) (velocity before emerging into the target). So option (b) is correct.
(c) Since velocity of the bullet is changed after hitting the target, so it follows a different parabolic path.
(d) As the velocity of the bullet changes to \(v^{\prime}\) which is less than \(v^{\prime}\) hence path followed will change and the bullet reaches at point \(B\) instead of \(A^{\prime}\), as shown in the figure.
(e) After emerging from the target, the bullet follows a parabollic path, the bullet will not fall vertically downward, so it is an incorrect option.
(f) As the bullet is passing through the target, the loss in energy of the \(\cdot\) bullet is transferred to particles of the target. Therefore, their internal energy increases. -
Question 41 of 41
41. Question
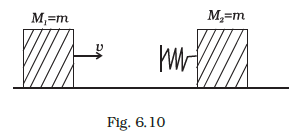
Two blocks \(M_1\) and \(M_2\) having equal mass are free to move on a horizontal frictionless surface. \(M_2\) is attached to a massless spring as shown in Fig. 6.10. Iniially \(M_2\) is at rest and \(M_1\) is moving toward \(M_2\) with speed \(v\) and collides head-on with \(M_2\).
 CorrectIncorrect
CorrectIncorrectHint
(c, d) If there is not specified we always consider the collision elastic.
When two bodies of equal masses collides elastically, their velocities are interchanged in these types of collision.
Kinetic energy and linear momentum remain conserved.
According to the above diagram when \(m_1\) comes in contact with the spring, \(m_1\) is retarded by the spring force and \(m_2\) is accelerated by the spring force.
(a) The spring will continue *to compress until the two blocks acquire common velocity. So some of kinetic energy of block \(M_x\) store into P.E and some part of it stores into K.E of block \(M_2\). So option (a) is incorrect.
(b) As surfaces are frictionalless momentum of the system will be conserved. So option (b) is also incorrect.
(c) The two bodies of equal mass exchange their velocities in a head on elastic collision between them. So, if spring is massless, the final state of the \(\)M_1\(\) is state of rest.
(d) Since there is a loss of K.E when the blocks collides on the rough surface. Hence, the collision is inelastic.