Past NEET Papers
Quiz Summary
0 of 86 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 86 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 86
1. Question
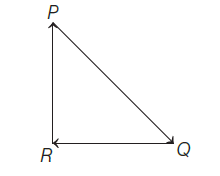
A particle moving with velocity \(\mathbf{v}\) is acted by three forces shown by the vector triangle \(P Q R\). The velocity of the particle will [NEET 2019]
 CorrectIncorrect
CorrectIncorrectHint
As the three forces are represented by three sides of a triangle forming a closed loop in the same order, then they will be in equilibrium and the net force is zero.
\(
\begin{aligned}
\Rightarrow \mathbf{F}_{\text {net }} &=\mathbf{F}_{P Q}+\mathbf{F}_{Q R}+\mathbf{F}_{R P}=0 \\
\mathbf{F}_{\text {net }} &=m \times \mathbf{a}=m \frac{d \mathbf{v}}{d t}=0 \Rightarrow \frac{d v}{d t}=0
\end{aligned}
\)
or \(\mathbf{v}=\) constant
Therefore, the velocity of the particle remains constant. -
Question 2 of 86
2. Question
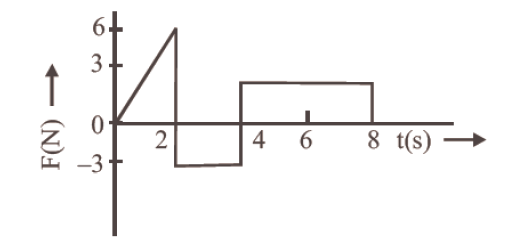
The force \(\mathrm{F}\) acting on a particle of mass \(\mathrm{m}\) is indicated by the force-time graph shown below. The change in momentum of the particle over the time interval from zero to \(8 \mathrm{~s}\) is: [CBSE AIPMT 2014]
 CorrectIncorrect
CorrectIncorrectHint
(d) Change in momentum = Area of F-t graph
\(\Delta p=\int \mathrm{Fdt}\)
\(=\) area of \(\Delta-area\) of \(\square+area\) of \(\square\)
\(
=\frac{1}{2} \times 2 \times 6-3 \times 2+4 \times 3=12 \mathrm{~N}\mathrm{s}
\)
Note: According to Newton’s 2nd law. \(F \propto \frac{d \vec{p}}{d t} \Rightarrow F\) \(=K \frac{d \vec{p}}{d t}\) or, \(F=\frac{d \vec{p}}{d t}[\because k=1, in S.I \& CGS system]\) and \(d \vec{p}=\vec{F} d t\) -
Question 3 of 86
3. Question
A stone is dropped from a height \(h\). It hits the ground with a certain momentum \(P\). If the same stone is dropped from a height \(100 \%\) more than the previous height, the momentum when it hits the ground will change by [CBSE AIPMT 2012]
CorrectIncorrectHint
(c) Momentum \(P=m v=m \sqrt{2 g h}\) (\(\therefore\ v^{2}=u^{2}+2 g h\); Here \(\left.u=0\right)\)
When the stone hits the ground its momentum,
\(P=m \sqrt{2 g h}\)
when same stone dropped from \(2 h\) then momentum,
\(
P^{\prime}=m \sqrt{2 g(2 h)}=\sqrt{2} P
\)
\(50 \%\) change in momentum, \(\frac{\left(P^{\prime}-P\right)}{P} \times 100 \%\)\(
\begin{aligned}
&\Rightarrow \quad\left(\frac{\sqrt{2} P-P}{P}\right) \times 100 \%=(\sqrt{2}-1) \times 100 \% \\
&\Rightarrow \quad(1.414-1) \times 100 \% \\
&\Rightarrow \quad 414 \times 100 \%=41.4 \%
\end{aligned}
\)
Which is changed by \(41 \%\) of the initial. -
Question 4 of 86
4. Question
A body of mass \(M\) hits normally a rigid wall with velocity \(V\) and bounces back with the same velocity. The impulse experienced by the body is [CBSE AIPMT 2011]
CorrectIncorrectHint
(a) Impulse experienced by the body = change in momentum
\(
=\mathrm{MV}-(-\mathrm{MV}) =2 \mathrm{MV}
\) -
Question 5 of 86
5. Question
A body under the action of a force \(\overrightarrow{\mathrm{F}}=6 \hat{\mathrm{i}}-8 \hat{\mathrm{j}}+10 \hat{\mathrm{k}}\), acquires an acceleration of \(1 \mathrm{~m} / \mathrm{s}^{2}\). The mass of this body must be [CBSE AIPMT 2009]
CorrectIncorrectHint
(c) \(\vec{F}=6 \hat{i}-8 \hat{j}+10 \hat{k}\),
\(
|\overrightarrow{\mathrm{F}}|=\sqrt{36+64+100}=10 \sqrt{2} \mathrm{~N}
\)\(\left(\because \mathrm{F}=\sqrt{\mathrm{F}_{\mathrm{x}}^{2}+\mathrm{F}_{\mathrm{y}}^{2}+\mathrm{F}_{\mathrm{z}}^{2}}\right)\)
Given, \(a=1 \mathrm{~ms}^{-2}\)
\(
\because \mathrm{F}=\mathrm{ma} \Rightarrow \mathrm{m}=\frac{10 \sqrt{2}}{1}=10 \sqrt{2} \mathrm{~kg}
\) -
Question 6 of 86
6. Question
Sand is being dropped on a conveyor belt at the rate of \(\mathrm{M} \mathrm{kg} / \mathrm{s}\). The force necessary to keep the belt moving with a constant velocity of \(\mathrm{v} \mathrm{m} / \mathrm{s}\) will be: [CBSE AIPMT 2008]
CorrectIncorrectHint
(a) \(\mathrm{F}=\frac{\mathrm{d}(\mathrm{Mv})}{\mathrm{dt}}=\mathrm{M} \frac{\mathrm{dv}}{\mathrm{dt}}+\mathrm{v} \frac{\mathrm{dM}}{\mathrm{dt}}\); Given \(\mathrm{v}\) is constant,
\(
\therefore \mathrm{F}=\mathrm{v} \frac{\mathrm{dM}}{\mathrm{dt}} \text { But } \frac{\mathrm{dM}}{\mathrm{dt}}=\mathrm{M kg} / \mathrm{s}
\)
\(
\therefore \mathrm{F}=\mathrm{Mv} \text { newton. }
\) -
Question 7 of 86
7. Question
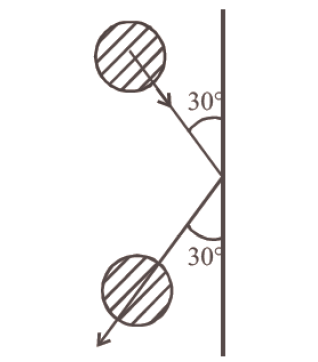
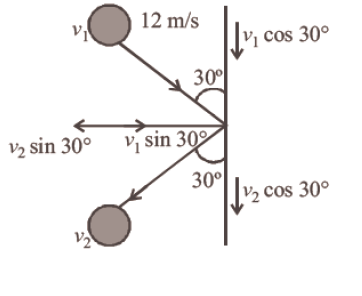
A \(0.5 \mathrm{~kg}\) ball moving with the speed of \(12 \mathrm{~m} / \mathrm{s}\) strikes a hard wall at an angle of \(30^{\circ}\) with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for \(0.25\) seconds, the average force acting on the wall is [CBSE AIPMT 2006]
 CorrectIncorrect
CorrectIncorrectHint
The magnitude of both velocity \(v_{1}\) and \(v_{2}\) are equal. Components of velocity along the wall are equal and are in the same direction.
But the components of velocity perpendicular to the wall are equal but opposite in direction.
So, the net change in momentum in the perpendicular direction,
\(
\Delta \mathrm{P}=m v_{1} \sin 30^{\circ}-\left(-m v_{2} \sin 30^{\circ}\right)
\)
\(\quad = 2 m v \sin 30^{\circ}\) \(\left[\left|v_{1}\right| v_{2} \mid\right]\)Average force acting on the wall will be given by
\(
\begin{aligned}
&\Rightarrow \quad F x t=2 m v \sin 30^{\circ} \\
&\Rightarrow \quad F=\frac{2 m v \sin 30^{\circ}}{t} \\
&\Rightarrow \quad F=\frac{2 \times 0.5^{2} \times 12 \times 1}{2 \times 0.25}=24 \\
&\quad F=24 \mathrm{~N}
\end{aligned}
\)
-
Question 8 of 86
8. Question
If \(a\) player catches a ball of mass \(150 \mathrm{gm}\) moving with a velocity of \(20 \mathrm{~m} / \mathrm{s}\), then he experiences a force of (Time taken to complete the catch is \(0.1 \mathrm{sec}\).) [CBSE AIPMT 2001]
CorrectIncorrectHint
Force imparted \(=\) rate of change of momentum
\(F=\frac{\Delta p}{\Delta t}\) or \(F=\frac{p_{1}-p_{2}}{\Delta t}\) or \(F=\frac{m\left(v_{1}-v_{2}\right)}{\Delta t}\)
Here, mass of body \(m=150 \mathrm{~g}=0.150 \mathrm{~kg}\),
\(
v_{1}=20 \mathrm{~m} / \mathrm{s} \text {, }
\)
\(
v_{2}=0
\)
\(
\begin{aligned}
&\text { Time taken, } \Delta t=0.1 \mathrm{~s} \\
&\therefore \quad F=\frac{0.150 \times(20-0)}{0.1}=30 \mathrm{~N}
\end{aligned}
\) -
Question 9 of 86
9. Question
A ball of mass \(3 \mathrm{~kg}\) moving with a speed of \(100 \mathrm{~m} / \mathrm{s}\), strikes a wall at an angle \(60^{\circ}\) (as shown in figure below). The ball rebounds at the same speed and remains in contact with the wall for \(0.2 \mathrm{~s}\), the force exerted by the ball on the wall is [CBSE AIPMT 2000]
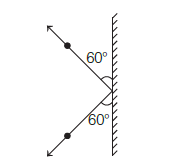 CorrectIncorrect
CorrectIncorrectHint
\(\begin{aligned}
&\text { (a) Change in momentum along the wall } \\
&=m v \cos 60^{\circ}-m v \cos 60^{\circ}=0 \\
&\text { Change in momentum perpendicular to the wall } \\
&=m v \sin 60^{\circ}-\left(-m v \sin 60^{\circ}\right)=2 m v \sin 60^{\circ} \\
&\therefore \text { Applied force }=\frac{\text { Change in momentum }}{\text { Time }} \\
&=\frac{2 m v \sin 60^{\circ}}{0.20} \\
&=\frac{2 \times 3 \times 10 \times \sqrt{3}}{2 \times 20}=50 \times 3 \sqrt{3} \\
&=150 \sqrt{3} \text { newton }
\end{aligned}\) -
Question 10 of 86
10. Question
A bullet is fired from a gun. The force on the bullet is given by \(F=600-2 \times 10^{5} t\) where, \(\mathrm{F}\) is in newton and \(t\) in second. The force on the bullet becomes zero as soon as it leaves the barrel. What is the average impulse imparted to the bullet? [CBSE AIPMT 1998]
CorrectIncorrectHint
To calculate impulse first of all calculate the time during which force becomes zero.
We are given,\(F=600-2 \times 10^{5} t\)
When the bullet leaves the barrel, the force on the bullet becomes zero.
\(
\begin{aligned}
600-2 \times 10^{5} t &=0 \Rightarrow t=\frac{600}{2 \times 10^{5}} \\
&=3 \times 10^{-3} \mathrm{~s}
\end{aligned}
\)
Then, average impulse imparted to the bullet
\(
\begin{aligned}
I &=\int_{0}^{t} F d t \\
&=\int_{0}^{3 \times 10^{-3}}\left(600-2 \times 10^{5} t\right) d t \\
&=\left[600 t-\frac{2 \times 10^{5} t^{2}}{2}\right]_{0}^{3 \times 10^{-3}} \\
&=600 \times 3 \times 10^{-3}-10^{5} \times\left(3 \times 10^{-3}\right)^{2} \\
&=1.8-0.9=0.9 \mathrm{~N}-\mathrm{s}
\end{aligned}
\) -
Question 11 of 86
11. Question
A \(5000 \mathrm{~kg}\) rocket is set for vertical firing. The exhaust speed is \(800 \mathrm{~ms}^{-1}\). To give an initial upward acceleration of \(20 \mathrm{~ms}^{-2}\), the amount of gas ejected per second to supply the needed thrust will be \(\left(g=10 \mathrm{~ms}^{-2}\right)\) [CBSE AIPMT 1998]
CorrectIncorrectHint
(b) Given : Mass of rocket \((\mathrm{m})=5000 \mathrm{~kg}\)
Exhaust speed \((v)=800 \mathrm{~m} / \mathrm{s}\)
Acceleration of rocket \(, a=20 \mathrm{~m} / \mathrm{s}^{2}\)
Gravitational acceleration, \( g=10 \mathrm{~m} / \mathrm{s}^{2}\)
Thrust, \(\Rightarrow \frac{v d m}{d t}\)
We know that upward force,
\(
F=m(g+a)=5000(10+20)
\)
\(
=5000 \times 30=150000 \mathrm{~N}
\)
This thrust gives upward force, \(F=\frac{v d m}{d t}\)
We also know that amount of gas ejected
\(
\Rightarrow\left(\frac{d m}{d t}\right)=\frac{F}{v}=\frac{150000}{800}=187.5 \mathrm{~kg} / \mathrm{s}
\) -
Question 12 of 86
12. Question
A \(10 \mathrm{~N}\) force is applied on a body produces an acceleration of \(1 \mathrm{~m} / \mathrm{s}^{2}\). The mass of the body is [CBSE AIPMT 1996]
CorrectIncorrectHint
(b) According to the second law of motion, the magnitude of the force can be calculated by.
Force \(F=m a\)
Here, \(F=10 \mathrm{~N}\)
\(
a=1 \mathrm{~m} / \mathrm{s}^{2} \Rightarrow \therefore m=\frac{F}{a}=\frac{10}{1}=10 \mathrm{~kg}
\) -
Question 13 of 86
13. Question
A ball of mass \(150 \mathrm{~g}\), moving with an acceleration \(20 \mathrm{~m} / \mathrm{s}^{2}\), is hit by a force, which acts on it for \(0.1\) sec. The impulsive force is [CBSE AIPMT 1996]
CorrectIncorrectHint
(b) Mass \(=150 \mathrm{gm}=\frac{150}{1000} \mathrm{~kg}\)
Force = Mass \(\times\) acceleration
\(
=\frac{150}{1000} \times 20 \mathrm{~N}=3 \mathrm{~N}
\)
Impulsive force \(=F \cdot \Delta t=3 \times 0.1=0.3 \mathrm{~N}\) -
Question 14 of 86
14. Question
If the force on a rocket moving with a velocity of \(300 \mathrm{~m} / \mathrm{sec}\) is \(345 \mathrm{~N}\), then the rate of combustion of the fuel, is [CBSE AIPMT 1995]
CorrectIncorrectHint
(c) Velocity of the rocket \(u=300 \mathrm{~m} / \mathrm{s}\) and force \(\mathrm{F}=345 \mathrm{~N}\). According to Newton’s second law, thrust (force) = Rate of change of linear momentum.
\(
\text { Rate of combustion of fuel } =\frac{F}{u}=\left(\frac{d m}{d t}\right)=\left(\frac{345}{300}\right)=1.15 \mathrm{~kg} / \mathrm{sec}
\) -
Question 15 of 86
15. Question
A satellite in a force free space sweeps stationary interplanetary dust at a rate \((\mathrm{dM} / \mathrm{dt})=\alpha v\). The acceleration of satellite is [CBSE AIPMT 1994]
CorrectIncorrectHint
(b) Thrust on the satellite is the force with which the satellite moves upwards in space. It is given by
\(
F=-u \frac{d m}{d t}
\)
Here, initial velocity \(u=v\), rate of change of mass \(\frac{d m}{d t}=\alpha v\)
As we know that,
\(
F=-v \frac{d m}{d t}=-v(\alpha v)=-\alpha v^{2}
\)
Acceleration \(=\frac{F}{M}=-\frac{\alpha v^{2}}{M}\) -
Question 16 of 86
16. Question
Physical independence of force is a consequence of [CBSE AIPMT 1991]
CorrectIncorrectHint
(b) According to Newton’s first law of motion, a body continues to be in a state of rest or of uniform motion, unless it is acted upon by an external force to change the state. Hence, Newton’s first law of motion is related to the physical independence of force.
-
Question 17 of 86
17. Question
A \(600 \mathrm{~kg}\) rocket is set for a vertical firing. If the exhaust speed is \(1000 \mathrm{~ms}^{-1}\), the mass of the gas ejected per second to supply the thrust needed to overcome the weight of the rocket is [CBSE AIPMT 1990]
CorrectIncorrectHint
(b) Thrust = weight
\(
\begin{aligned}
&\Rightarrow \frac{u d M}{d t}=m g \Rightarrow \frac{d M}{d t}=\frac{m g}{u} \\
&=\frac{600 \times 10}{1000}=6 \mathrm{~kg} \mathrm{~s}^{-1}
\end{aligned}
\) -
Question 18 of 86
18. Question
A particle of mass \(m\) is moving with a uniform velocity \(v_{1}\). It is given an impulse such that its velocity becomes \(v_{2}\). The impulse is equal to [CBSE AIPMT1990]
CorrectIncorrectHint
(d) Impulse = final momentum – initial momentum \(=m\left(v_{2}-v_{1}\right)\)
-
Question 19 of 86
19. Question
Two bodies of mass \(4 \mathrm{~kg}\) and \(6 \mathrm{~kg}\) are tied to the ends of a massless string. The string passes over a pulley which is frictionless (shown in the figure). The acceleration of the system in terms of acceleration due to gravity \(g\) is [NEET 2020]
CorrectIncorrectHint
(b) Given : Mass \(m_{1}=4 \mathrm{~kg}\) and \(m_{2}=6 \mathrm{~kg}\).
Acceleration of the system,
\(
\begin{aligned}
&a=\frac{\left(m_{2}-m_{1}\right) g}{\left(m_{2}+m_{1}\right)} \\
&\therefore a=\frac{(6-4) g}{6+4}=\frac{g}{5}
\end{aligned}
\) -
Question 20 of 86
20. Question
Two blocks A and B of masses \(3 m\) and \(m\) respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in the figure. The magnitudes of acceleration of A and B immediately after the string is cut, are respectively [NEET 2017]
CorrectIncorrectHint
(b) \(k x=\mathrm{mg}+3 \mathrm{mg}\)
Force on string,
\(\Rightarrow k x=4 \mathrm{mg}\)
After cutting the string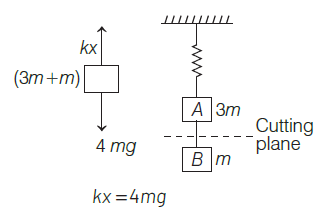
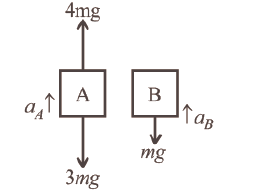
For block A: \(3 m a_{A}=4 \mathrm{mg}-3 \mathrm{mg}\)
\(a_{A}=\frac{4 m g-3 m g}{3 m}=\frac{g}{3}\)
\(
a_{A}=\frac{g}{3}
\)
For block B: \(m a_{B}=m g\); \(a_{B}=g\) -
Question 21 of 86
21. Question
One end of a string of length \(l\) is connected to a particle of mass \(m\) and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in a circle with speed \(v\) the net force on the particle (directed towards centre) will be (T represents the tension in the string): [CBSE AIPMT 2017]
CorrectIncorrectHint
(a) Net force on particle in uniform circular motion is centripetal force \(\left(\frac{m v^{2}}{\ell}\right)\) which is provided by tension in string so the net force will be equal to tension i.e., \(\mathrm{T}\).
-
Question 22 of 86
22. Question
Three blocks A, B, and C of masses \(4 \mathrm{~kg}, 2 \mathrm{~kg}\) and \(1 \mathrm{~kg}\) respectively, are in contact on a frictionless surface, as shown. If a force of \(14 \mathrm{~N}\) is applied on the \(4 \mathrm{~kg}\) block then the contact force between A and B is [CBSE AIPMT 2015]
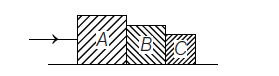 CorrectIncorrect
CorrectIncorrectHint
(b) Given, \(m_{A}=4 \mathrm{~kg}\)
\(m_{B}=2 \mathrm{~kg} \Rightarrow m_{C}=1 \mathrm{~kg}\)
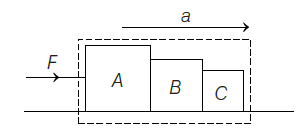
So, total mass \(M=4+2+1=7 \mathrm{~kg}\)
Now, \(\quad F=M a \Rightarrow 14=7 a \Rightarrow a=2 \mathrm{~m} / \mathrm{s}^{2}\)
FBD of block A,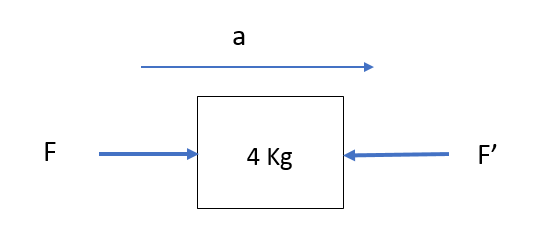
\(\begin{aligned}
&F-F^{\prime}=4 a \\
&F^{\prime}=14-4 \times 2 \Rightarrow F^{\prime}=6 \mathrm{~N}
\end{aligned}\) -
Question 23 of 86
23. Question
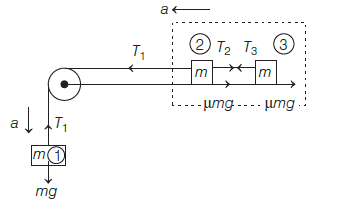
A system consists of three masses \(m_{1}, m_{2}\) and \(m_{3}\) connected by a string passing over a pulley P. The mass \(m_{1}\) hangs freely and \(m_{2}\) and \(m_{3}\) are on a rough horizontal table (the coefficient of friction \(=\mu\) ). The pulley is friction less and of negligible mass. The downward acceleration of mass \(m_{1}\) is (Assume, \(m_{1}=m_{2}=m_{3}=m\) ) [CBSE AIPMT 2014]
CorrectIncorrectHint
(c) First of all, consider the forces on the blocks
For the Ist block, \(\quad\left[\because m_{1}=m_{2}=m_{3}\right]\)
\(
m g-T_{1}=m \times a \dots (i)
\)
Let us consider 2 nd and 3rd block as a system.
So, \(T_{1}-2 \mu m g=2 m \times a \dots (ii)\)
Solving Eqs. (i) and (ii),
\(
\begin{aligned}
&\Rightarrow \quad m g-T_{1}=m \times a \\
&\Rightarrow T_{1}-2 \mu m g=2 m \times a
\end{aligned}
\)
Addiing Eqs. (i) and (ii)
\(
m g(1-2 \mu)=3 m \times a \Rightarrow a=\frac{g}{3}(1-2 \mu)
\)
-
Question 24 of 86
24. Question
A balloon with mass \(m\) is descending down with an acceleration \(\mathrm{a}\) (where \(\mathrm{a}<\mathrm{g}\) ). How much mass should be removed from it so that it starts moving up with an acceleration \(a\)? [CBSE AIPMT 2014]
CorrectIncorrectHint
(a) Let upthrust of air be \(F_{a}\) then
When, the balloon is descending down with acceleration a from the free body diagram
\(\mathrm{F}_{\mathrm{a}}=\mathrm{mg}-\mathrm{ma} \Rightarrow F a=m(g-a) \dots (i)\)
For upward motion, \( F_{a}-(\mathrm{m}-\Delta \mathrm{m}) g=(\mathrm{m}-\Delta \mathrm{m}) a \dots (ii)\)
From equation (i) and (ii),
Therefore, \(\Delta \mathrm{m}=\frac{2 m a}{(g+a)}\) -
Question 25 of 86
25. Question
Three blocks with masses \(\mathrm{m}, 2 \mathrm{~m}\) and \(3 \mathrm{~m}\) are connected by strings as shown in the figure. After an upward force \(F\) is applied on block \(m\), the masses move upward at constant speed \(\mathrm{v}\). What is the net force on the block of mass \(2 \mathrm{~m}\) ? ( \(\mathrm{g}\) is the acceleration due to gravity) [CBSE AIPMT 2013]
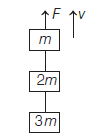 CorrectIncorrect
CorrectIncorrectHint
(d) Since all the blocks are moving with constant velocity and we know that, if velocity is constant, acceleration of the body becomes zero. Hence, the net force on all the blocks will be zero.
-
Question 26 of 86
26. Question
A person of mass \(60 \mathrm{~kg}\) is inside a lift of mass \(940 \mathrm{~kg}\) and presses the button on control panel. The lift starts moving upwards with an acceleration \(1.0 \mathrm{~m} / \mathrm{s}^{2}\). If \(\mathrm{g}=10 \mathrm{~ms}^{-2}\), the tension in the supporting cable is [CBSE AIPMT 2011]
CorrectIncorrectHint
(c) Total mass m
\(
\begin{aligned}
&=\text { Mass of lift }+\text { Mass of person } \\
&=940+60=1000 \mathrm{~kg}
\end{aligned}
\)
So, from the free body diagram below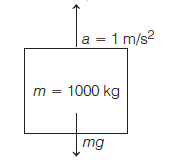
Hence, \(T-1000 \times 10=1000 \times 1\)
\(
T=11000 \mathrm{~N}
\) -
Question 27 of 86
27. Question
Three forces acting on a body are shown in the figure. To have the resultant force only along the \(y\)-direction, the magnitude of the minimum additional force needed is [CBSE AIPMT 2008]
CorrectIncorrectHint
(a) The components of \(1 \mathrm{~N}\) and \(2 \mathrm{~N}\) forces along \(+x\)-axis \(=1 \cos 60^{\circ}+2 \sin 30^{\circ}\) \(=1 \times \frac{1}{2}+2 \times \frac{1}{2}=\frac{1}{2}+1=\frac{3}{2}=1.5 \mathrm{~N}\)
The component of \(4 \mathrm{~N}\) force along \(-x\)-axis \(=4 \sin 30^{\circ}=4 \times \frac{1}{2}=2 \mathrm{~N}\).
Therefore, if a force of \(0.5 \mathrm{~N}\) is applied along \(+x\) axis, the resultant force along \(x\)-axis will become zero and the resultant force will be obtained only along \(y\)-axis.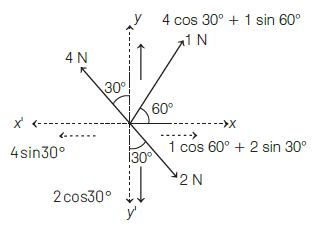
-
Question 28 of 86
28. Question
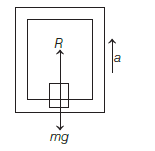
The mass of a lift is \(2000 \mathrm{~kg}\). When the tension in the supporting cable is \(28000 \mathrm{~N}\), then its acceleration is: [CBSE AIPMT 2009]
CorrectIncorrectHint
(a) Here, the lift is accelerating upward at the rate of a. Hence, the equation of motion is written as
\(
\begin{gathered}
R-m g=m a \\
28000-20000=2000 a \\
\quad\left[\because g=10 \mathrm{~ms}^{-2}\right] \\
\Rightarrow \quad a=\frac{8000}{2000}=4 \mathrm{~ms}^{-2} \text { upwards }
\end{gathered}
\)
-
Question 29 of 86
29. Question
The coefficient of static friction, \(\mu_{s}\), between block A of mass \(2 \mathrm{~kg}\) and the table as shown in the figure, is \(0.2\). What would be the maximum mass value of block B so that the two blocks do not move? The string and the pulley are assumed to be smooth and massless \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\) [CBSE AIPMT 2004]
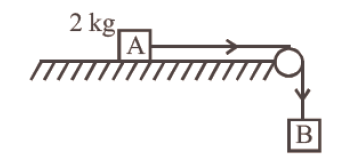 CorrectIncorrect
CorrectIncorrectHint
(d) Condition for the max value of the mass of block B so that two blocks do not move is,
\(
\begin{aligned}
&m_{B} g=\mu_{s} m_{A} g \\
&\Rightarrow m_{B}=\mu_{s} m_{A} \\
&\text { or, } m_{B}=0.2 \times 2=0.4 \mathrm{~kg}
\end{aligned}
\) -
Question 30 of 86
30. Question
A block of mass \(m\) is placed on a smooth wedge of inclination \(\theta\). The whole system is accelerated horizontally so that the block does not slip on the wedge. The force exerted by the wedge on the block ( \(\mathrm{g}\) is the acceleration due to gravity) will be [CBSE AIPMT 2004]
CorrectIncorrectHint
(b) According to the condition,

\(\mathrm{N}=m a \sin \theta+m g \cos \theta\) \dots (i)
Also, \(m g \sin \theta=m a \cos \theta\) \dots (ii)
From (i) \& (ii), \(a=g \tan \theta\)
\(
\begin{aligned}
\therefore N &=m g \frac{\sin ^{2} \theta}{\cos \theta}+m g \cos \theta . \\
&=\frac{m g}{\cos \theta}\left(\sin ^{2} \theta+\cos ^{2} \theta\right)=\frac{m g}{\cos \theta}
\end{aligned}
\)Note: The condition for the body to be at rest relative to the inclined plane, \(a=g \sin \theta-b \operatorname{cos} \theta=0\) Horizontal acceleration, \(b=g \tan \theta\).
-
Question 31 of 86
31. Question
A man weighing \(80 \mathrm{~kg}\), stands on a weighing scale in a lift which is moving upwards with a uniform acceleration of \(5 \mathrm{~m} / \mathrm{s}^{2}\). What would be the reading on the scale? \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right) \quad\) [CBSE AIPMT 2003]
CorrectIncorrectHint
(a) Reading of the scale = Apparent wt. of the man \(=m(g+a)\)
\(
=80(10+5)=1200 \mathrm{~N}
\) -
Question 32 of 86
32. Question
A monkey of mass \(20 \mathrm{~kg}\) is holding a vertical rope. The rope will not break when a mass of 25 \(\mathrm{kg}\) is suspended from it but will break if the mass exceeds \(25 \mathrm{~kg}\). What is the maximum acceleration with which the monkey can climb up along the rope? \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right) \) [CBSE AIPMT 2003]
CorrectIncorrectHint
(a) Maximum bearable tension in the rope \(T=25 \times 10=250 \mathrm{~N}\)
From the figure below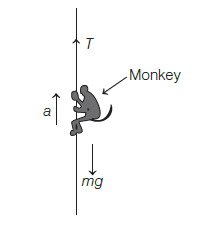
\(T-m g=m a \quad\) or acceleration \(a=\frac{T-m g}{m}\)
Given, mass \(m=20 \mathrm{~kg}\),
\(
g=10 \mathrm{~m} / \mathrm{s}^{2} \text {, }
\)Taking, \(T=250 \mathrm{~N}\)
Hence, \(a=\frac{250-20 \times 10}{20}=\frac{50}{20}\) \(=2.5 \mathrm{~m} / \mathrm{s}^{2}\) -
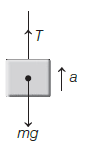
Question 33 of 86
33. Question
A lift weighing \(1000 \mathrm{~kg}\) is moving upwards with an accelertion of \(1 \mathrm{~m} / \mathrm{s}^{2}\). The tension in the supporting cable is [CBSE AIPMT 2002]
CorrectIncorrectHint
(b) When lift move upwards with the same acceleration, then according to free body diagram of the left \(T-m g=m a\) or \(T=m(g+a)\)
Given,
\(
m=1000 \mathrm{~kg}, a=1 \mathrm{~m} / \mathrm{s}^{2} \text {, }
\)
\(
g=9.8 \mathrm{~m} / \mathrm{s}^{2}
\)
Thus, \(T=1000(9.8+1)=1000 \times 10.8\)
\(
=10800 \mathrm{~N}
\)
-
Question 34 of 86
34. Question
Two blocks \(m_{1}=5 \mathrm{gm}\) and \(m_{2}=10 \mathrm{gm}\) are hung vertically over a light frictionless pulley as shown here. What is the acceleration of the masses when they are left free? (where \(\mathrm{g}\) is acceleration due to gravity) [CBSE AIPMT 2000]
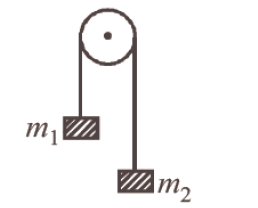 CorrectIncorrect
CorrectIncorrectHint
\(\text { (a) Let } \mathrm{T} \text { be the tension in the string. }\)
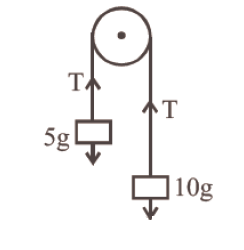
\(
\begin{aligned}
&\therefore 10 \mathrm{~g}-\mathrm{T}=10 a \dots (i)\\
&T-5 g=5 a \dots (ii)
\end{aligned}
\)
Adding (i) and (ii),
\(
5 g=15 a \Rightarrow a=\frac{g}{3} \mathrm{~m} / \mathrm{s}^{2}
\)
Note: When the pulley have a finite mass \(m\) then acceleration,
\(
a=\frac{m_{1}-m_{2}}{m_{1}+m_{2}+\frac{m}{2}}
\) -
Question 35 of 86
35. Question
A mass of \(1 \mathrm{~kg}\) is suspended by a thread. It is
(i) lifted up with an acceleration \(4.9 \mathrm{~m} / \mathrm{s}^{2}\),
(ii) lowered with an acceleration \(4.9 \mathrm{~m} / \mathrm{s}^{2}\).
The ratio of the tensions is [CBSE AIPMT 1998]CorrectIncorrectHint
(a)
(i) When, mass is lifted upwards with an acceleration a, then according to free body diagram\(\begin{aligned}
T_{1}-m g &=m a \Rightarrow T_{1}=m g+m a \\
T_{1} &=m(g+a)
\end{aligned}\)
Substituting the values, we obtain \(\therefore \quad T_{1}=(1)(9.8+4.9)=14.7 \mathrm{~N}\)
(ii) When, mass is lowered downwards with an acceleration a, then
\(
\begin{gathered}
m g-T_{2}=m a \\
\Rightarrow T_{2}=m g-m a=m(g-a)
\end{gathered}
\)
Substituting the values, we have
Then, ratio of tensions
\(
\frac{T_{1}}{T_{2}}=\frac{14.7}{4.9}=\frac{3}{1} \Rightarrow T_{1}: T_{2}=3: 1
\) -
Question 36 of 86
36. Question
A monkey is decending from the branch of a tree with constant acceleration. If the breaking strength is \(75 \%\) of the weight of the monkey, the minimum acceleration with which the monkey can slide down without breaking the branch is [CBSE AIPMT 1993]
CorrectIncorrectHint
(c) Let \(\mathrm{T}\) be the tension in the branch of a tree when monkey is descending with acceleration a. Then \(\mathrm{mg}-T=m a\); and \(T=75 \%\) of weight of monkey,
\(
\therefore m a=m g-\left(\frac{75}{100}\right) m g=\left(\frac{1}{4}\right) m g
\)
or \(a=\frac{g}{4}\). -
Question 37 of 86
37. Question
A body of mass \(m\) is kept on a rough horizontal surface (coefficient of friction \(=\mu\) ). A horizontal force is applied to the body, but it does not move. The resultant of normal reaction and the frictional force acting on the object is given \(F\), where \(F\) is [NEET (Odisha) 2019]
CorrectIncorrectHint
We can draw the situation in the following diagram
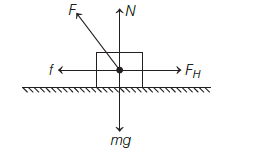
The frictional force, \(f=\mu N=\mu \mathrm{mg}\)
\(
[\because N=m g]
\)
From the Free body diagram(FBD), the resultant force is
\(
\begin{aligned}
|\mathbf{F}| &=\sqrt{N^{2}+f^{2}} \\
&=\sqrt{(m g)^{2}+(\mu m g)^{2}} \\
&=m g \sqrt{1+\mu^{2}}
\end{aligned}
\)
This is the minimum force required to move the object. But as the body is not moving
\(
\therefore \quad|\mathbf{F}| \leq m g \sqrt{1+\mu^{2}}
\) -
Question 38 of 86
38. Question
Which one of the following statements is incorrect? [NEET 2018]
CorrectIncorrectHint
(d) Coefficient of friction or sliding friction has no dimension.
\(
f=\mu_{\mathrm{s}} \mathrm{N} \Rightarrow \mu_{\mathrm{s}}=\frac{f}{N}=\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0}\right]
\) -
Question 39 of 86
39. Question
A block of mass \(m\) is placed on a smooth inclined wedge \(A B C\) of inclination \(\theta\) as shown in the figure. The wedge is given an acceleration towards the right. The relation between \(a\) and \(\theta\) for the block to remain stationary on the wedge is [NEET 2018]
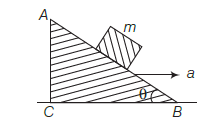 CorrectIncorrect
CorrectIncorrectHint
Since the wedge is accelerating towards the right with a, thus a pseudo force acts in the left direction in order to keep the block stationary. As the system is in equilibrium.
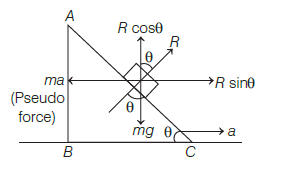
\(\begin{aligned}
& \therefore & \Sigma F_{x} &=0 \\
\text { or } & & \Sigma F_{y} &=0 \\
\Rightarrow & R \sin \theta &=m a \\
\text { or } & m g \sin \theta &=m a \dots (i) \\
\text { Similarly, } & R \cos \theta &=m g
\end{aligned}\)
or \(m g \cos \theta=m g \dots (ii)\)
Dividing Eq. (i) by Eq (ii), we get
\(
\begin{aligned}
\frac{m g \sin \theta}{m g \cos \theta} &=\frac{m a}{m g} \\
\Rightarrow \quad \tan \theta &=\frac{a}{g}
\end{aligned}
\) -
Question 40 of 86
40. Question
A block A of mass \(\mathrm{m}_{1}\) rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of the table and from its other end, another block B of mass \(\mathrm{m}_{2}\) is suspended. The coefficient of kinetic friction between the block and the table is \(\mu_{\mathrm{k}}\). When the block A is sliding on the table, the tension in the string is [CBSE AIPMT 2015]
CorrectIncorrectHint
\(\begin{aligned}
&\text { (b) For the motion of both the blocks }\\
&m_{1} \mathrm{a}=\mathrm{T}-\mu_{\mathrm{k}} \mathrm{m}_{1} \mathrm{~g}\\
&m_{2} g-T=m_{2} a\\
&\mathrm{a}=\frac{\mathrm{m}_{2} \mathrm{~g}-\mu_{\mathrm{k}} \mathrm{m}_{1} \mathrm{~g}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\\
&\mathrm{m}_{2} \mathrm{~g}-\mathrm{T}=\left(\mathrm{m}_{2}\right)\left(\frac{\mathrm{m}_{2} \mathrm{~g}-\mu_{\mathrm{k}} \mathrm{m}_{1} \mathrm{~g}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\right)\\
&\text { solving we get tension in the string }\\
&\mathrm{T}=\frac{\mathrm{m}_{1} \mathrm{~m}_{2} \mathrm{~g}\left(1+\mu_{\mathrm{k}}\right) \mathrm{g}}{\mathrm{m}_{1}+\mathrm{m}_{2}}
\end{aligned}\)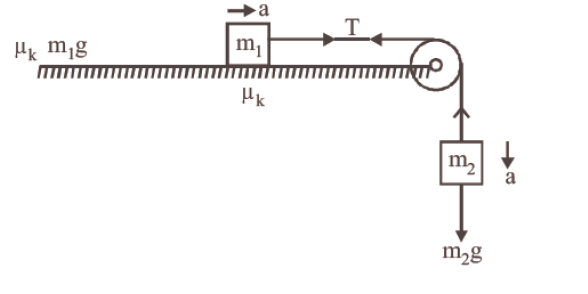
-
Question 41 of 86
41. Question
A plank with a box on it at one end is gradually raised about the other end. As the angle of inclination with the horizontal reaches \(30^{\circ}\) the box starts to slip and slides \(4.0 \mathrm{~m}\) down the plank in \(4.0 \mathrm{~s}\). The coefficients of static and kinetic friction between the box and the plank will be, respectively: [CBSE AIPMT 2015]
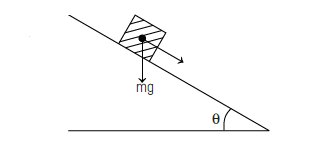 CorrectIncorrect
CorrectIncorrectHint
(a) Coefficient of static friction, $\mu_{s}=\tan \theta$
\(
\Rightarrow \mu_{s}=\tan 30^{\circ}=\frac{1}{\sqrt{3}}=0.577 \cong 0.6
\)So, distance covered by plank,
\(
\mathrm{S}=u t+\frac{1}{2} \mathrm{at}^{2}
\)
where, \(u=0\) and [/latex]a=g \sin \theta-\mu_{k}(g) \cos \theta[/latex]
\(
\begin{aligned}
&4=\frac{1}{2} a(4)^{2} \Rightarrow a=\frac{1}{2}=0.5 \\
&{\left[\because \theta=30^{\circ}, s=4 \mathrm{~m} \text { and } t=4 \mathrm{~s} \text { given }\right]} \\
&\Rightarrow \mu_{k}=\frac{0.9}{\sqrt{3}}=0.5
\end{aligned}
\) -
Question 42 of 86
42. Question
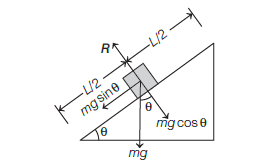
The upper half of an inclined plane of inclination \(\theta\) is perfectly smooth while the lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom if the coefficient of friction between the block and the lower half of the plane is given by [CBSE AIPMT 2013]
CorrectIncorrectHint
(b) Net work done by the block in going from top to bottom of the inclined plane, must be equal to the work done by frictional force. The block may be stationary, when \(m g \sin \theta \cdot L=\mu m g \cos \theta \frac{L}{2}\)
or
\(
\begin{aligned}
\mu &=\frac{m g \sin \theta \cdot L}{m g \cos \theta \cdot \frac{L}{2}} \\
&=2 \frac{\sin \theta}{\cos \theta}=2 \tan \theta \\
\mu &=2 \tan \theta
\end{aligned}
\)
-
Question 43 of 86
43. Question
A conveyor belt is moving at a constant speed of \(2 \mathrm{~m} / \mathrm{s}\). A box is gently dropped on it. The coefficient of friction between them is \(\mu=0.5\). The distance that the box will move relative to the belt before coming to rest on it taking \(\mathrm{g}=10 \mathrm{~ms}^{-2}\), is [CBSE AIPMT 2011]
CorrectIncorrectHint
(c) Frictional force on the box \(f=\mu \mathrm{mg}\)
\(\therefore\) Acceleration in the box, \(a=\frac{f}{m}=\frac{\mu m g}{m}\)
\(
\begin{aligned}
& \mathrm{a}=\mu \mathrm{g}=5 \mathrm{~ms}^{-2} \\
& \mathrm{v}^{2}=\mathrm{u}^{2}+2 \mathrm{as} \\
\Rightarrow \quad & 0=2^{2}+2 \times(5) \mathrm{s} \\
\Rightarrow & \mathrm{s}=-\frac{2}{5} \text { w.r.t. belt } \\
\Rightarrow & \text { distance }=0.4 \mathrm{~m}
\end{aligned}
\) -
Question 44 of 86
44. Question
A block of mass \(m\) is in contact with the cart \(C\) as shown in the Figure below. [CBSE AIPMT 2010]
The coefficient of static friction between the block and the cart is \(\mu\). The acceleration \(\alpha\) of the cart that will prevent the block from falling satisfies: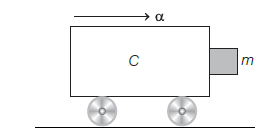 CorrectIncorrect
CorrectIncorrectHint
(c) Forces acting on the block are as shown in the figure below. Normal reaction \(\mathrm{N}\) is provided by the force ma due to acceleration \(\alpha\)
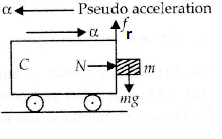
For the block not to fall, frictional force,
\(
\begin{aligned}
&f_{r} \geq \mathrm{mg} \\
&\Rightarrow \quad \mu \mathrm{N} \geq \mathrm{mg} \\
&\Rightarrow \quad \mu \mathrm{m\alpha} \geq \mathrm{mg} \\
&\Rightarrow \quad \alpha \geq \mathrm{g} / \mu
\end{aligned}
\) -
Question 45 of 86
45. Question
A block B is pushed momentarily along a horizontal surface with an initial velocity of V. If \(\mu\) is the coefficient of sliding friction between B and the surface, block B will come to rest after a time [CBSE AIPMT 2007]
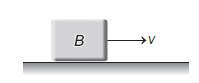 CorrectIncorrect
CorrectIncorrectHint
(d) Block B will come to rest, if the force applied to it will vanish due to frictional force acting between block B and the surface, i.e. frictional force = force applied
\(
\begin{array}{ll}
\text { i.e. } & \mu m g=m a \\
\text { or } & \mu m g=m\left(\frac{v}{t}\right) \text { or } t=\frac{v}{\mu g}
\end{array}
\) -
Question 46 of 86
46. Question
A \(100 \mathrm{~N}\) force acts horizontally on a block of \(10 \mathrm{~kg}\) placed on a horizontal rough surface of coefficient of friction \(\mu=0.5\). If the acceleration due to gravity \((\mathrm{g})\) is taken as 10 \(\mathrm{ms}^{-2}\), the acceleration of the block (in \(\mathrm{ms}^{-2}\) ) is [CBSE AIPMT 2002]
CorrectIncorrectHint
(b) \(a=\frac{F-\mu R}{m}=\frac{100-0.5 \times(10 \times 10)}{10}=5 \mathrm{~ms}^{-2}\)
-
Question 47 of 86
47. Question
A block of mass \(1 \mathrm{~kg}\) is placed on a truck which accelerates with acceleration \(5 \mathrm{~m} / \mathrm{s}^{2}\). The coefficient of static friction between the block and truck is \(0.6\). The frictional force acting on the block is [CBSE AIPMT 2001]
CorrectIncorrectHint
(a) Maximum friction force \(=\mu \mathrm{mg}\) \(=.6 \times 1 \times 9.8=5.88 \mathrm{~N}\)
But here required friction force \(=m a=1 \times 5=5 \mathrm{~N}\) -
Question 48 of 86
48. Question
A person slides freely down a frictionless inclined plane while his bag falls down vertically from the same height. The final speeds of the \(\operatorname{man}\left(V_{M}\right)\) and the bag \(\left(V_{B}\right)\) should be such that [CBSE AIPMT 2000]
CorrectIncorrectHint
(b) As there is only a gravitational field that works. We know it is a conservative field and depends only on the endpoints. So, \(V_{M}=V_{B}\)
-
Question 49 of 86
49. Question
A block has been placed on an inclined plane with the slope angle \(\theta\), and the block slides down the plane at a constant speed. The coefficient of kinetic friction is equal to [CBSE AIPMT 1993]
CorrectIncorrectHint
(d) The angle of repose or angle of sliding is defined as the minimum angle of inclination of a plane with the horizontal, such that a body placed on the plane just begins to slide down.
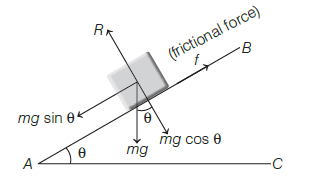
\(A B\) is an inclined plane such that a body placed on it just begins to slide down
\(\angle B A C=\theta=\) angle of repose
In equilibrium,
\(
\begin{aligned}
& f =m g \sin \theta \\
\text { and } & R =m g \cos \theta \\
\therefore & \frac{f}{R} =\frac{m g \sin \theta}{m g \cos \theta}=\tan \theta \\
\text { i.e. } & \mu =\tan \theta
\end{aligned}
\) -
Question 50 of 86
50. Question
Consider a car moving along a straight horizontal road with a speed of \(72 \mathrm{~km} / \mathrm{h}\). If the coefficient of static friction between the tires and the road is \(0.5\), the shortest distance in which the car can be stopped is (taking \(g=10\) \(\mathrm{m} / \mathrm{s}^{2}\) ) [CBSE AIPMT 1992]
CorrectIncorrectHint
(b) Here \(\mathrm{u}=72 \mathrm{~km} / \mathrm{h}=20 \mathrm{~m} / \mathrm{s} ; \mathrm{v}=0\); \(a=-\mu g=-0.5 \times 10=-5 \mathrm{~m} / \mathrm{s}^{2}\)
As \(v^{2}=u^{2}+2 a s\),
\(
\therefore \quad s=\frac{\left(v^{2}-u^{2}\right)}{2 a}=\frac{\left(0-(20)^{2}\right.}{2 \times(-5)}=40 \mathrm{~m}
\) -
Question 51 of 86
51. Question
A heavy uniform chain lies on the horizontal tabletop. If the coefficient of friction between the chain and the table surface is \(0.25\), then the maximum fraction of the length of the chain that can hang over one edge of the table is [CBSE AIPMT 1991]
CorrectIncorrectHint
(a) The force of friction should balance the weight of the chain hanging. If M is the mass of the whole chain of length L and x is the length of the chain hanging to balance, and \(\mu\) is the coefficient of friction then
\(
\begin{array}{ll}
& \mu \frac{M}{L}(L-x) g=\frac{M}{L} x g \\
\text { or } & \mu(L-x)=x \\
\text { or } & x=\frac{\mu L}{\mu+1}=\frac{0.25 L}{1.25} \quad(A s, \mu=0.25) \\
\therefore & x=\frac{L}{5} \text { or } \frac{x}{L}=\frac{1}{5}=\frac{1}{5} \times 100=20 \%
\end{array}
\) -
Question 52 of 86
52. Question
A block of mass \(10 \mathrm{~kg}\) is in contact against the inner wall of a hollow cylindrical drum of radius \(1 \mathrm{~m}\). The coefficient of friction between the block and the inner wall of the cylinder is \(0.1\). The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be: \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\) [NEET 2019]
CorrectIncorrectHint
(c) Given the mass of the block, \(\mathrm{m}=10 \mathrm{~kg}\); radius of a cylindrical drum, \(\mathrm{r}-1 \mathrm{~m}\); coefficient of friction between the block and the inner wall of the cylinder \(\mu=0.1\);
Minimum angular velocity \(\omega_{\text {min }}\)From the below figure, it can be concluded that the block will be stationary when the limiting friction \(\left(f_{L}\right)\) is equal to or greater than the downward force or weight of the block, i.e.
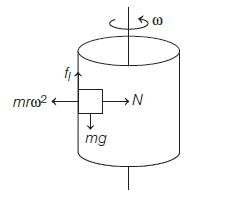
\(
\begin{aligned}
&\mathrm{f}_{\mathrm{L}} \geq \mathrm{mg} \\
&\Rightarrow \mu \mathrm{N} \geq \mathrm{mg} \\
&\Rightarrow \mu \mathrm{r} \omega^{2} \geq \mathrm{mg}
\end{aligned}
\)
Hrere, \(\mathrm{N}=\mathrm{mr} \omega^{2}\)
or, \(\mathrm{m} \geq \sqrt{\frac{\mathrm{g}}{\mathrm{r} \mu}}\)
\(
\begin{aligned}
&\text { or, } \omega_{\min }=\sqrt{\frac{\mathrm{g}}{\mathrm{r} \mu}} \\
&\therefore \omega_{\min }=\sqrt{\frac{10}{0.1 \times 1}}=10 \mathrm{rad} / \mathrm{s}
\end{aligned}
\) -
Question 53 of 86
53. Question
Starting from rest, a body slides down a \(45^{\circ}\) inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is [CBSE AIPMT 1988]
CorrectIncorrectHint
When, a plane is inclined to the horizontal at an angle \(\theta\), which is greater than the angle of repose, the body placed on the inclined plane slides down with an acceleration a.
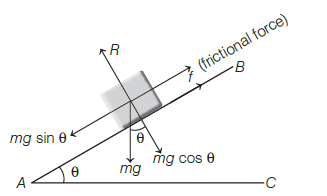
As it is clear from the figure
\(R=m g \cos \theta \dots (i)\)
Net force on the body down the inclined plane which means it is sliding downwards
\(F=m g \sin \theta-f \dots (ii)\)i.e. \(\quad F=m a=m g \sin \theta-\mu R \quad(f=\mu R) \\\) \(\therefore \quad m a=m g \sin \theta-\mu m g \cos \theta\) \(=m g(\sin \theta-\mu \cos \theta)\) Hence, \(a=g(\sin \theta-\mu \cos \theta)\) \(\therefore\) Time taken by body to slide down the plane \(\quad t_{1}=\sqrt{\frac{2 s}{a}}=\sqrt{g(\sin \theta-\mu \cos \theta)}\)
When friction is absent, then time taken to slide down the plane
\(t_{2}=\sqrt{\frac{2 s}{g \sin \theta}} \Rightarrow \because t_{1}=2 t_{2} \quad\) (given)
\(\therefore \quad t_{1}^{2}=4 t_{2}^{2}\)
or \(\frac{2 s}{g(\sin \theta-\mu \cos \theta)}=\frac{2 s \times 4}{g \sin \theta}\)
or \(\sin \theta=4 \sin \theta-4 \mu \cos \theta\)
or \(\mu=\frac{3}{4} \tan \theta=\frac{3}{4} \tan 45^{\circ}\)
\(\therefore \quad \mu=\frac{3}{4}=0.75\) -
Question 54 of 86
54. Question
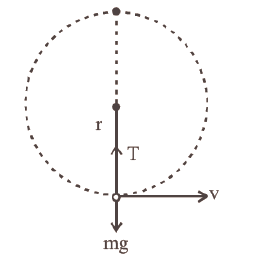
A mass \(m\) is attached to a thin wire and whirled in a vertical circle. The wire is most likely to break when: [CBSE AIPMT 2014]
CorrectIncorrectHint
\(\begin{aligned}
&\text { (c) } \mathrm{T}-\mathrm{mg}=\frac{\mathrm{mv}^{2}}{\mathrm{r}}[\text { centripetal force }]=\frac{\mathrm{mv}^{2}}{\mathrm{r}} \\
&\Rightarrow \quad \mathrm{T}=\mathrm{mg}+\frac{\mathrm{mv}^{2}}{\mathrm{r}}
\end{aligned}\)As the velocity is maximum at the lowest point so tension is maximum at the lowest position of the mass. so, the chance of breaking is maximum.
-
Question 55 of 86
55. Question
A car is negotiating a curved road of radius \(R\). The road is banked at an angle \(\theta\). the coefficient of friction between the tires of the car and the road is \(\mu_{s}\). The maximum safe velocity on this road is: [CBSE AIPMT 2016]
CorrectIncorrectHint
(b) According to the question, a car is negotiating a curved road of radius \(R\). The road is banked at angle \(\theta\) and the coefficient of friction between the tires of the car and the road is \(\mu_{s}\). So, this given situation can be drawn as shown in the figure below.
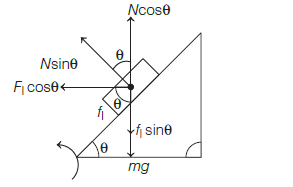
Considering the case of vertical equilibrium
\(\quad N \cos \theta=m g+f_{l} \sin \theta\) \(\Rightarrow \quad m g=N \cos \theta-f_{l} \sin \theta \quad \ldots\) (i) Considering the case of horizontal equilibrium, \(\quad N \sin \theta+f_{l} \cos \theta=\frac{m v^{2}}{R} \quad\)…(ii)
Divide eqs. (i) and (ii), we get
\(
\begin{aligned}
\frac{v^{2}}{R g} &=\frac{\sin \theta+\mu_{s} \cos \theta}{\cos \theta-\mu_{s} \sin \theta} \\
\Rightarrow \quad v &=\sqrt{R g\left(\frac{\sin \theta+\mu_{s} \cos \theta}{\cos \theta-\mu_{s} \sin \theta}\right)} \\
\Rightarrow \quad v &=\sqrt{R g\left(\frac{\tan \theta+\mu_{s}}{1-\mu_{s} \tan \theta}\right)}
\end{aligned}
\) -
Question 56 of 86
56. Question
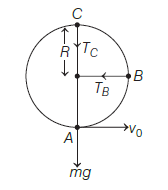
What is the minimum velocity with which a body of mass \(\mathrm{m}\) must enter a vertical loop of radius \(\mathrm{R}\) so that it can complete the loop? [CBSE AIPMT 2016]
CorrectIncorrectHint
(d) According to the question, we have
Let the tension at point \(A\) be \(T_{A}\). So, from Newton’s second law
\(
T_{A}-m g=\frac{m v_{c}^{2}}{R}
\)
Energy at point \(A=\frac{1}{2} m v_{0}^{2}\)
Energy at point \(C\) is
\(
\frac{1}{2} m v_{c}^{2}+m g \times 2 R
\)Applying Newton’s 2nd law at point \(C\)
\(
T_{c}+m g=\frac{m v_{c}^{2}}{R}
\)
To complete the loop \(T_{c} \geq 0\)
So, \(m g=\frac{m v_{c}^{2}}{R}\)
\(\Rightarrow v_{c}=\sqrt{g R}\)
From Eqs. (i) and (ii)by conservation of energy
\(
\begin{aligned}
& \frac{1}{2} m v_{0}^{2} &=\frac{1}{2} m v_{c}^{2}+2 m g R \\
\Rightarrow \quad & \frac{1}{2} m v_{0}^{2} &=\frac{1}{2} m g R+2 m g R \times 2 \\
\Rightarrow \quad & v_{0}^{2} &=g R+4 g R \\
\Rightarrow \quad & v_{0} &=\sqrt{5 g R}
\end{aligned}
\)
-
Question 57 of 86
57. Question
Two stones of masses \(\mathrm{m}\) and \(2 \mathrm{~m}\) are whirled in horizontal circles, the heavier one in radius \(\frac{r}{2}\) and the lighter one in radius \(r\). The tangential speed of lighter stone is \(\mathrm{n}\) times that of the value of heavier stone when they experience same centripetal forces. The value of \(\mathrm{n}\) is : [CBSE AIPMT 2015]
CorrectIncorrectHint
(d) According to question, two stones experience same centripetal force
i.e., \(\mathrm{F}_{\mathrm{C}_{1}}=\mathrm{F}_{\mathrm{C}_{2}}\)
or, \(\frac{\mathrm{mv}_{1}^{2}}{\mathrm{r}}=\frac{2 \mathrm{mv}_{2}^{2}}{(\mathrm{r} / 2)} \quad\) or, \(\mathrm{V}_{1}^{2}=4 \mathrm{~V}_{2}^{2}\)
So, \(\mathrm{V}_{1}=2 \mathrm{~V}_{2}\) i.e., \(n=2\) -
Question 58 of 86
58. Question
A car is moving in a circular horizontal track of radius \(10 \mathrm{~m}\) with a constant speed of \(10 \mathrm{~m} /\) s. A bob is suspended from the roof of the car by a light wire of length \(1.0 \mathrm{~m}\). The angle made by the wire with the vertical is [NEET Kar. 2013]
CorrectIncorrectHint
(d) Given; speed \(=10 \mathrm{~m} / \mathrm{s}\); radius \(r=10 \mathrm{~m}\)
Angle made by the wire with the vertical is \(\theta\).
Then, \(\mathrm{T} \cos \theta=\mathrm{mg}\)
\(
\begin{aligned}
&\mathrm{T} \sin \theta=\frac{m v^{2}}{r} \\
&\text { So, } \\
&\tan \theta=\frac{v^{2}}{r g}=\frac{10^{2}}{10 \times 10}=1 \quad \frac{m v^{2}}{r} \\
&\Rightarrow \theta=45^{\circ}=\frac{\pi}{4}
\end{aligned}
\) -
Question 59 of 86
59. Question
A car of mass \(1000 \mathrm{~kg}\) negotiates a banked curve of radius \(90 \mathrm{~m}\) on a frictionless road. If the banking angle is \(45^{\circ}\), the speed of the car is: [CBSE AIPMT 2012]
CorrectIncorrectHint
(b) The angle of banking
\(
\tan \theta=\frac{v^{2}}{r g}
\)
Given, \(\quad \theta=45^{\circ}\)
Radius of banked curve road
\(
\begin{array}{rl}
r=90 & \mathrm{~m} \text { and } g=10 \mathrm{~m} / \mathrm{s}^{2} \\
\Rightarrow \quad \tan 45^{\circ} & =\frac{v^{2}}{90 \times 10} \\
v & =\sqrt{90 \times 10 \times \tan 45^{\circ}} \\
& =\sqrt{90 \times 10 \times 1}=30 \mathrm{~m} / \mathrm{s}
\end{array}
\) -
Question 60 of 86
60. Question
A car of mass \(m\) is moving on a level circular track of radius \(R\). If \(\mu_{s}\) represents the static friction between the road and tires of the car, the maximum speed of the car in circular motion is given by: [CBSE AIPMT 2012]
CorrectIncorrectHint
(d) For smooth driving maximum speed of car \(v\) then,
\(
\begin{aligned}
&\frac{m v^{2}}{R}=\mu_{s} m g \\
&v=\sqrt{\mu_{s} R g}
\end{aligned}
\) -
Question 61 of 86
61. Question
A \(500 \mathrm{~kg}\) car takes a round turn of radius \(50 \mathrm{~m}\) with a velocity of \(36 \mathrm{~km} / \mathrm{h}\). The centripetal force is [CBSE AIPMT 1999]
CorrectIncorrectHint
(c) Centripetal force \(=\frac{m v^{2}}{r}=\frac{500 \times(10)^{2}}{50}\)
\(
=1000 \mathrm{~N} \quad[\because 36 \mathrm{~km} / \mathrm{hr}=10 \mathrm{~m} / \mathrm{s}]
\) -
Question 62 of 86
62. Question
A body of mass \(0.4 \mathrm{~kg}\) is whirled in a vertical circle making \(2 \mathrm{rev} / \mathrm{sec}\). If the radius of the circle is \(1.2 \mathrm{~m}\), then tension in the string when the body is at the top of the circle, is [CBSE AIPMT 1999]
CorrectIncorrectHint
(a) Given : Mass \(m=0.4 \mathrm{~kg}\)
Its frequency \(n=2 \mathrm{rev} / \mathrm{sec}\)
Radius \(r=1.2 \mathrm{~m}\). We know that linear velocity of the body \((v)=\omega r=(2 \pi n) r\)
\(
=2 \times 3.14 \times 2 \times 1.2=15.08 \mathrm{~m} / \mathrm{s} \text {. }
\)
Therefore, tension in the string when the body is at the top of the circle (T)
\(
\begin{aligned}
&=\frac{\mathrm{mv}^{2}}{\mathrm{r}}-\mathrm{mg}=\frac{0.4 \times(15.08)^{2}}{2}-(0.4 \times 9.8) \\
&=45.78-3.92=41.56 \mathrm{~N}
\end{aligned}
\) -
Question 63 of 86
63. Question
What will be the maximum speed of a car on a road turn of radius \(30 \mathrm{~m}\) if the coefficient of friction between the tires and the road is \(0.4\) (Take \(\mathrm{g}=9.8 \mathrm{~m} / \mathrm{s}^{2}\) ) [CBSE AIPMT 1995]
CorrectIncorrectHint
(a) \(r=30 \mathrm{~m}\) and \(\mu=0.4\).
\(
v_{\max }=\sqrt{\mu r g}=\sqrt{0.4 \times 30 \times 9.8}=10.84 \mathrm{~m} / \mathrm{s}
\) -
Question 64 of 86
64. Question
A particle of mass \(M\) is moving in a horizontal circle of radius \(R\) with uniform speed \(\mathrm{V}\). When it moves from one point to a diametrically opposite point, it’s [CBSE AIPMT 1992]
CorrectIncorrectHint
(c) On the diametrically opposite points, the velocities have the same magnitude but in opposite directions. Therefore, the change in momentum is MV \(-(-M V)=2 \mathrm{MV}\)
-
Question 65 of 86
65. Question
When milk is churned, the cream gets separated due to [CBSE AIPMT 1991]
CorrectIncorrectHint
(b) Cream gets separated from churned milk due to centrifugal force.
Note: Centrifugal force is a pseudo force that is equal and opposite to the centripetal force. Centripetal force can be a mechanical, electrical, or magnetic force.
-
Question 66 of 86
66. Question
A ball of mass \(0.15 \mathrm{~kg}\) is dropped from a height \(10 \mathrm{~m}\), strikes the ground and rebounds to the same height. The magnitude of impulse imparted to the ball is nearly \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\) [NEET 2021]
CorrectIncorrectHint
(b) Given, the mass of the ball dropped from the height, \(m=0.15 \mathrm{~kg}\)
The height from the ball dropped,
\(h=10 \mathrm{~m}\)
We know that,
\(\mid\) mpulse \(|=m| \Delta \bar{v} \mid\)
where, \(\quad \Delta \bar{v}=v_{2}-v_{1}\)
Here, \(v_{2}\) is velocity reaches to the same height,
\(v_{1}\) is velocity just before striking to the ground.For case (1), ball dropped from the \(10 \mathrm{~m}\) height and strikes to the ground. Now, the velocity of the ball just before striking to the ground is
\(
\begin{aligned}
&\quad v_{1}=-\sqrt{2 g h} \\
&\Rightarrow \quad v_{1}=-\sqrt{2(10)(10)} \\
&\Rightarrow \quad v_{1}=-10 \sqrt{2} \mathrm{~m} / \mathrm{s} \\
&\text { For case }(2) \text { ball rebounds to the same } \\
&\text { height. } \\
&\text { The velocity with which the ball just } \\
&\text { reaches to the same height, } \\
&\qquad v_{2}=\sqrt{2 g h} \\
&\Rightarrow \quad v_{2}=\sqrt{2(10)(10)} \\
&\Rightarrow \quad \quad v_{2}=10 \sqrt{2} \mathrm{~m} / \mathrm{s}
\end{aligned}
\)Now, magnitude of the impulse imparted to the ball,
\(
\begin{aligned}
\text { |lmpulse } \mid &=m|\Delta \bar{v}| \\
&=0.15|10 \sqrt{2}-(-10 \sqrt{2})| \\
&=0.15|2 \times 10 \sqrt{2}| \\
&=4.2 \mathrm{~kg}-\mathrm{m} / \mathrm{s}
\end{aligned}
\) -
Question 67 of 86
67. Question
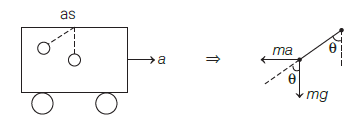
A truck is stationary and has a bob suspended by a light string, in a frame attached to the truck. The truck suddenly moves to the right with an acceleration of a. The pendulum will tilt [NEET (Odisha) 2020]
CorrectIncorrectHint
(b) As the truck move to the right, so the bob will move to the left due to inertia of rest with acceleration a. From the diagram below as the string moves by an angle of \(\theta\) with the vertical then the tangent angle is
\(
\tan \theta=\frac{m a}{m g} \Rightarrow \theta=\tan ^{-1}\left(\frac{a}{g}\right)
\)
-
Question 68 of 86
68. Question
A rigid ball of mass \(m\) strikes a rigid wall at \(60^{\circ}\) and gets reflected without loss of speed as shown in the figure. The value of impulse imparted by the wall on the ball will be [NEET 2016]
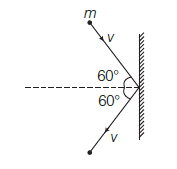 CorrectIncorrect
CorrectIncorrectHint
(a) As we know, the impulse is imparted due to changes in perpendicular components of the momentum of the ball.
\(
\begin{aligned}
&J=\Delta p=m v_{f}-m v_{i} \\
&=m v \cos 60^{\circ}-\left(-m v \cos 60^{\circ}\right) \\
&=2 m v \cos 60^{\circ}=2 m v \times \frac{1}{2}=m v
\end{aligned}
\) -
Question 69 of 86
69. Question
A bullet of mass \(10 \mathrm{~g}\) moving horizontal with a velocity of \(400 \mathrm{~m} / \mathrm{s}\) strikes a woodblock of mass \(2 \mathrm{~kg}\) which is suspended by light inextensible string of length \(5 \mathrm{~m}\). As result, the centre of gravity of the block found to rise a vertical distance of \(10 \mathrm{~cm}\). The speed of the bullet after it emerges of horizontally from the block will be [NEET 2016]
CorrectIncorrectHint
(c) According to the law of conservation of momentum, \(p_{i}=p_{f}\)
\(
\Rightarrow \quad(0.01) \times 400+0=2 v+(0.01) v^{\prime} \ldots \text { (i) }
\)
Also, velocity \(v\) of the block just after the collision is
\(
\begin{aligned}
&\quad v=\sqrt{2 g h}=\sqrt{2 \times 10 \times 0.1}=\sqrt{2} \quad \text {…(ii) } \\
&\Rightarrow \text { From Eqs. (i) and (ii), we have } \\
&\quad v^{\prime} \approx 120 \mathrm{~m} / \mathrm{s}
\end{aligned}
\) -
Question 70 of 86
70. Question
An explosion breaks a rock into three parts in a horizontal plane. Two of them go off at right angles to each other. The first part of mass \(1 \mathrm{~kg}\) moves with a speed of 12 \(\mathrm{ms}^{-1}\) and the second part of mass \(2 \mathrm{~kg}\) moves with \(8 \mathrm{~ms}^{-1}\) speed. If the third part flies off with \(4 \mathrm{~ms}^{-1}\) speed, then its mass is [NEET 2013]
CorrectIncorrectHint
(b) Momentum is conserved before and after the collision.
We have, \(\mathbf{p}_{1}+\mathbf{p}_{2}+\mathbf{p}_{3}=0 \quad[\because p=m v]\)
\(
\begin{array}{lrlr}
\therefore & & 1 \times 12 \mathbf{i}+2 \times 8 \mathbf{j}+\mathbf{p}_{3}=0 \\
\Rightarrow & & 12 \hat{\mathbf{i}}+16 \hat{\mathbf{j}}+\mathbf{p}_{3}=0 \\
\Rightarrow & & \mathbf{p}_{3} =-(12 \mathbf{i}+16 \mathbf{j}) \\
& \therefore & \mathbf{p}_{3} =\sqrt{(12)^{2}+(16)^{2}} \\
& & =\sqrt{144+256} \\
& & =20 \mathrm{~kg}-\mathrm{m} / \mathrm{s} \\
& \text { Now, } & \mathbf{p}_{3} =m_{3} v_{3} \\
\Rightarrow & & m_{3} =\frac{\mathbf{p}_{3}}{v_{3}}=\frac{20}{4}=5 \mathrm{~kg}
\end{array}
\) -
Question 71 of 86
71. Question
Two spheres A and B of masses \(m_{1}\) and \(m_{2}\) respectively collide. A is at rest initially and B is moving with velocity \(v\) along \(x\)-axis. After the collision, B has a velocity \(\frac{v}{2}\) in a direction perpendicular to the original direction. The mass A moves after collision in the direction [CBSE AIPMT 2012]
CorrectIncorrectHint
(c) Here, \(\mathbf{p}_{1}=m_{2} v \mathbf{i}+m_{1} \times 0\)
\(
\mathbf{p}_{f}=m_{2} \frac{v}{2} \hat{\mathbf{j}}+m_{1} \times \mathbf{v}_{1}
\)
Law of conservation of momentum\(\begin{aligned}
\mathbf{p}_{i} &=\mathbf{p}_{f} \\
m_{2} v \hat{\mathbf{i}} &=m_{2} \frac{v}{2} \hat{\mathbf{j}}+m_{1} \times \mathbf{v}_{1} \\
\mathbf{v}_{1} &=\frac{m_{2}}{m_{1}} v \hat{\mathbf{i}}+\frac{m_{2}}{m_{1}} \frac{v}{2} \hat{\mathbf{j}}
\end{aligned}\)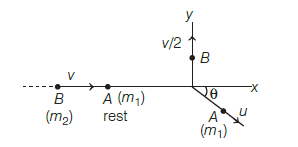
From this equation, we can find \(\tan \theta=\frac{y}{x}=\frac{1}{2}, \theta=\tan ^{-1}\left(\frac{1}{2}\right)\) to the \(x\)-axis. -
Question 72 of 86
72. Question
A man of \(50 \mathrm{~kg}\) mass is standing in a gravity-free space at a height of \(10 \mathrm{~m}\) above the floor. He throws a stone of \(0.5 \mathrm{~kg}\) mass downwards with a speed \(2 \mathrm{~ms}^{-1}\). When the stone reaches the floor, the distance of the man above the floor will be [CBSE AIPMT 2010]
CorrectIncorrectHint
(b) As, \(m r=\) constant
\(m_{1} r_{1}=m_{2} r_{2}\)
\(\Rightarrow \quad r_{2}=\frac{m_{1} r_{1}}{m_{2}}=\frac{0.5 \times 10}{50}=0.1\)
So, distance travelled by the man will be \(10+0.1=10.1 \mathrm{~m}\) -
Question 73 of 86
73. Question
An object of mass \(3 \mathrm{~kg}\) is at rest. If a force \(\mathbf{F}=\left(6 t^{2} \hat{\mathbf{i}}+4 t \hat{\mathbf{j}}\right) \mathrm{N}\) is applied on the object, then the velocity of the object at \(t=3 \mathrm{~s}\) is [CBSE AIPMT 2002]
CorrectIncorrectHint
(b) According to Newton’s 2nd law, force applied on an object is equal to the rate of change of momentum.
\(
\begin{array}{ll}
\text { i.e. } \quad & \mathbf{F}=\frac{d \mathbf{p}}{d t} \\
\text { or } & \mathbf{F}=m \frac{d v}{d t} \dots (i)
\end{array}
\)
Given, \(m=3 \mathrm{~kg}, t=3 \mathrm{~s}, \mathbf{F}=\left(6 \mathrm{t}^{2} \hat{\mathbf{i}}+4 \mathrm{t} \hat{\mathbf{j}}\right) \mathrm{N}\)
Substituting these values in Eq. (i), we get
\(
\left(6 t^{2} \hat{\mathbf{i}}+4 t \hat{\mathbf{j}}\right)=3 \frac{d \mathbf{v}}{d t}
\)
or \(\quad d \mathbf{v}=\frac{1}{3}\left(6 t^{2} \hat{\mathbf{i}}+4 \hat{\mathbf{j}}\right) d \mathrm{t}\)
Now, taking integration of both sides, we get
\(
\begin{aligned}
\int d \mathbf{v} &=\int_{0}^{t} \frac{1}{3}\left(6 t^{2} \hat{\mathbf{i}}+4 \hat{\mathbf{j}}\right) d t \\
\mathbf{v} &=\frac{1}{3} \int_{0}^{t}\left(6 t^{2} \hat{\mathbf{i}}+4 \hat{\mathbf{j}}\right) d t
\end{aligned}
\)\(\begin{aligned}
&\text { but } t=3 s \quad \text { (given) }\\
&\therefore \quad \mathbf{v}=\frac{1}{3} \int_{0}^{3}\left(6 t^{2} \hat{\mathbf{i}}+4 \hat{\mathrm{j}}\right) d t\\
&\mathbf{v}=\frac{1}{3}\left[\frac{6 t^{3}}{3} \hat{\mathbf{i}}+\frac{4 t^{2}}{2} \hat{\mathbf{j}}\right]_{0}^{3}\\
&\mathbf{v}=\frac{1}{3}\left[2(3)^{3} \hat{\mathbf{i}}+2(3)^{2} \hat{\mathbf{j}}\right]\\
&\mathbf{v}=\frac{1}{3}[54 \hat{\mathbf{i}}+18 \hat{\mathbf{j}}]\\
&\text { or } \mathbf{v}=18 \hat{\mathbf{i}}+6 \hat{\mathbf{j}}
\end{aligned}\) -
Question 74 of 86
74. Question
1 kg body explodes into three fragments. The ratio of their masses is \(1: 1: 3\). The fragments of the same mass move perpendicular to each other with speeds \(30 \mathrm{~m} / \mathrm{s}\), while the heavier part remains in the initial direction. The speed of the heavier part is [CBSE AIPMT 2001]
CorrectIncorrectHint
(b) Apply conservation of momentum with direction.
Let \(u\) be the velocity and \(\theta\) the direction of the third piece as shown.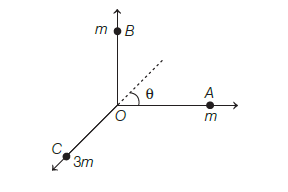
The square of momentum of third piece is equal to sum of squares of momentum first and second pieces.
\(
\begin{aligned}
p_{3}^{2} &=p_{1}^{2}+p_{2}^{2} \\
\text { or } \quad p_{3} &=\sqrt{p_{1}^{2}+p_{2}^{2}} \\
& \text { or } \quad 3 m v_{3} &=\sqrt{(m \times 30)^{2}+(m \times 30)^{2}} \\
\text { or } & v_{3} &=\frac{30 \sqrt{2}}{3}=10 \sqrt{2} \mathrm{~m} / \mathrm{s}
\end{aligned}
\) -
Question 75 of 86
75. Question
A particle of mass \(1 \mathrm{~kg}\) is thrown vertically upwards with speed \(100 \mathrm{~m} / \mathrm{s}\). After \(5 \mathrm{~s}\), it explodes into two parts. One part of mass \(400 \mathrm{~g}\) comes back with speed \(25 \mathrm{~m} / \mathrm{s}\), what is the speed of other part just after explosion? [CBSE AIPMT 2000]
CorrectIncorrectHint
(a) According to 1 st equation of motion, velocity of particle after \(5 \mathrm{~s}\)
\(
\begin{aligned}
v &=u-g t \\
v &=100-10 \times 5 \\
&=100-50=50 \mathrm{~m} / \mathrm{s} \quad \text { (upwards) }
\end{aligned}
\)
Applying conservation of linear momentum gives
\(
M v=m_{1} v_{1}+m_{2} v_{2} \dots (i)
\)
Taking upward direction positive, the velocity \(v_{1}\) will be negative.
\(
\therefore \quad v_{1}=-25 \mathrm{~m} / \mathrm{s}, \quad v=50 \mathrm{~m} / \mathrm{s}
\)
Also, \(M=1 \mathrm{~kg}, \mathrm{~m}_{1}=400 \mathrm{~g}=0.4 \mathrm{~kg}\)
and \(m_{2}=\left(M-m_{1}\right)=1-0.4=0.6 \mathrm{~kg}\)
Thus, Eq. (i) becomes,
\(
\begin{aligned}
1 \times 50 &=0.4 \times(-25)+0.6 v_{2} \\
\text { or } \quad 50 &=-10+0.6 v_{2}
\end{aligned}
\)or \(0.6 v_{2}=60\) or \(v_{2}=\frac{60}{0.6}=100 \mathrm{~m} / \mathrm{s}\)
As \(v_{2}\) is positive, therefore the other part will move upwards with a velocity of \(100 \mathrm{~m} / \mathrm{s}\). -
Question 76 of 86
76. Question
The force on a rocket moving with a velocity \(300 \mathrm{~m} / \mathrm{s}\) is \(210 \mathrm{~N}\). The rate of consumption of fuel of rocket is [CBSE AIPMT 1999]
CorrectIncorrectHint
(a) Whenever there is change in the mass w.r.t. time, apply \(F=-v \frac{d m}{d t}\)
Thrust force on the rocket
\(F_{t}=v_{r}\left(-\frac{d m}{d t}\right)\) (upwards)
Rate of combustion of fuel
\(
\begin{aligned}
&\text { Rate of combustion of fuel } \\
&\qquad \frac{d m}{d t}=\frac{F_{t}}{v_{r}} \\
&\text { Given, } \quad \begin{aligned}
F_{t} &=210 \mathrm{~N} \\
v_{r} &=300 \mathrm{~m} / \mathrm{s} \\
-\frac{d m}{d t} &=\frac{210}{300}=0.7 \mathrm{~kg} / \mathrm{s}
\end{aligned}
\end{aligned}
\) -
Question 77 of 86
77. Question
A satellite in a force free space sweeps stationary interplanetary dust at a rate. \(\left(\frac{\mathrm{dM}}{\mathrm{dt}}\right)=\alpha v\). The acceleration of satellite is [CBSE AIPMT 1994]
CorrectIncorrectHint
(b) Thrust on the satellite is the force with which the satellite moves upwards in space. It is given by \(F=-u \frac{d m}{d t}\)
Here, initial velocity \(u=v\), rate of change of mass \(\frac{d m}{d t}=\alpha v\)
As we know,
\(
F=-v \frac{d m}{d t}=-v(\alpha v)=-\alpha v^{2}
\)
Acceleration \(=\frac{F}{M}=-\frac{\alpha v^{2}}{M}\) -
Question 78 of 86
78. Question
Calculate the acceleration of the block and trolly system shown in the figure. The coefficient of kinetic friction between the trolly and the surface is \(0.05 .(g=10\) \(\mathrm{m} / \mathrm{s}^{2}\), mass of the string is negligible and no other friction exists). [NEET 2020]
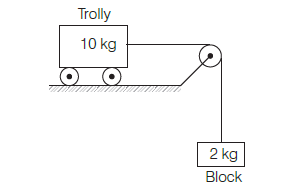 CorrectIncorrect
CorrectIncorrectHint
(a) The given situation is shown in the following diagram.
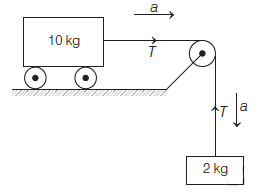
If \(a\) be the acceleration of the system then, equation of motion of \(10 \mathrm{~kg}\) trolly,
\(
\begin{gathered}
T-\mu R=10 a \\
\Rightarrow \quad T-0.05 \times 10 g=10 a \\
{[\because \mu=0.05, R=10 g]} \\
\Rightarrow \quad T-0.05 \times 10 \times 10=10 a \\
T – 5 =10 a \dots (i)\\
\text { Equation of motion of } 2 \mathrm{~kg} \text { block, } \\
2 g-T=2 a \\
2 \times 10-T=2 a \\
20-T=2 a \dots (ii)\\
\text { Adding Eqs. (i) and (ii), we have } \\
20-5=12 a \\
15=12 a \\
\Rightarrow \quad a=\frac{15}{12}=\frac{5}{4}=1.25 \mathrm{~ms}^{-2}
\end{gathered}
\) -
Question 79 of 86
79. Question
A block of mass \(10 \mathrm{~kg}\) is placed on a rough horizontal surface having coefficient of friction \(\mu=0.5\). If a horizontal force of \(100 \mathrm{~N}\) is applied on it, then the acceleration of the block will be \(\left(\right.\) Takeg \(=10 \mathrm{~m} / \mathrm{s}^{2}\) ) [CBSE AIPMT 2002]
CorrectIncorrectHint
(c) Free body diagram of the block is
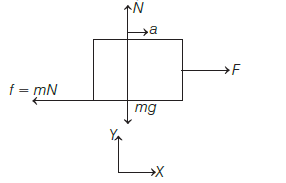
From Newton’s second law along \(X\)-axis
i.e. \(\quad F-f=m a\)
or \(\quad F-\mu m g=m a\)
or \(\quad a=\frac{F-\mu m g}{m}\)
Given, \(F=100 \mathrm{~N}, \mu=0.5, m=10 \mathrm{~kg}\),
\(
g=10 \mathrm{~m} / \mathrm{s}^{2}
\)
Substituting, the values in the above relation for the acceleration of block,
\(
a=\frac{(100)-(0.5)(10)(10)}{(10)}=5 \mathrm{~m} / \mathrm{s}^{2}
\) -
Question 80 of 86
80. Question
Consider, a car moving along a straight horizontal road with a speed of \(72 \mathrm{~km} / \mathrm{h}\). If the coefficient of static friction between the tires and the road is \(0.5\), the shortest distance in which the car can be stopped is (Take \(g=10 \mathrm{~m} / \mathrm{s}^{2}\) ) [CBSE AIPMT 1992]
CorrectIncorrectHint
(b) When static friction is present, then the acceleration of a body is given by \(a=-\mu \mathrm{g}\) Here, initial velocity
\(
\mathrm{u}=72 \mathrm{~km} \mathrm{~h}^{-1}=72 \times \frac{5}{18}=20 \mathrm{~m} / \mathrm{s}
\)
Final velocity \(v=0\)
\(
\therefore \quad a=-\mu g=-0.5 \times 10=-5 \mathrm{~m} / \mathrm{s}^{2}
\)
Now, from third equation of motion,
i.e. \(v^{2}=u^{2}+2\) as
\(
\mathrm{s}=\frac{v^{2}-u^{2}}{2 a}=\frac{0-(20)^{2}}{2 \times(-5)}=40 \mathrm{~m}
\) -
Question 81 of 86
81. Question
A uniform circular disc of radius 50 \(\mathrm{cm}\) at rest is free to turn about an axis that is perpendicular to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of \(2.0 \mathrm{rad} \mathbf{s}^{-2}\). Its net acceleration in \(\mathbf{m s}^{-2}\) at the end of \(2.0 \mathrm{~s}\) is a approximately [NEET 2016]
CorrectIncorrectHint
(d) According to given question, a uniform circular disc of radius \(50 \mathrm{~cm}\) at rest is free to turn about an axis having perpendicular to its plane and passes through its centre.
\(\therefore\) Angular acceleration, \(\alpha=2\) rad s \(^{-2}\) (given)
Angular speed, \(\omega=\alpha t=4 \mathrm{rad} \mathrm{s}^{-1}\)
because Centripetal acceleration, \(a_{c}=\omega^{2} r\) \(=(4)^{2} \times 0.5\)
\(=16 \times 0.5\)
\(a_{c}=8 \mathrm{~m} / \mathrm{s}^{2}\)
because Linear acceleration at the end of \(2 \mathrm{~s}\),
\(
a_{t}=\alpha r=2 \times 0.5 \Rightarrow a_{t}=1 \mathrm{~m} / \mathrm{s}^{2}
\)
Therefore, the net acceleration at the end of \(2.0 \mathrm{~s}\) is given by\(\begin{gathered}
a=\sqrt{a_{c}^{2}+a_{t}^{2}} \\
a=\sqrt{(8)^{2}+(1)^{2}}=\sqrt{65} \Rightarrow a \approx 8 \mathrm{~m} / \mathrm{s}^{2}
\end{gathered}\) -
Question 82 of 86
82. Question
A gramophone record is revolving with an angular velocity \(\omega\). A coin is placed at a distance \(r\) from the centre of the record. The static coefficient of friction is \(\mu\). The coin will revolve with the record if [CBSE AIPMT 2010]
CorrectIncorrectHint
(c) When the disc spins, the frictional force between the gramophone record and coin is \(\mu \mathrm{mg}\). The coin will revolve with the record, if
\(F_{\text {frictional }} \geq F_{\text {centripetal }}\)
i.e. \(\mu m g \geq m \omega^{2} r\)
\(
\frac{\mu g}{r} \geq \omega^{2}
\) -
Question 83 of 86
83. Question
A ball of mass \(0.25 \mathrm{~kg}\) attached to the end of a string of length \(1.96 \mathrm{~m}\) is moving in a horizontal circle. The string will break if the tension is more than \(25 \mathrm{~N}\). What is the maximum speed with which the ball can be moved? [CBSE AIPMT 1998]
CorrectIncorrectHint
(a) For a ball to move in a horizontal circle, the ball should satisfy the condition
Tension in the string = Centripetal force
\(
\begin{aligned}
&\Rightarrow \quad T_{\max }=\frac{M v_{\max }^{2}}{R} \\
&\Rightarrow \quad v_{\max }=\sqrt{\frac{T_{\max } \cdot R}{M}}
\end{aligned}
\)
Making substitution, we obtain
\(
v_{\max }=\sqrt{\frac{25 \times 1.96}{0.25}}=\sqrt{196}=14 \mathrm{~m} / \mathrm{s}
\)
In a vertical circle, the tension at the highest point is zero and at the lowest point is maximum. -
Question 84 of 86
84. Question
Two racing cars of masses \(m\) and \(4 \mathrm{~m}\) are moving in circles of radii \(r\) and \(2 r\) respectively. If their speeds are such that each makes a complete circle in the same time, then the ratio of the angular speeds of the first to the second [CBSE AIPMT 1995]
CorrectIncorrectHint
(d) As both cars take the same time to complete the circle and as \(\omega=\frac{2 \pi}{t}\), therefore the ratio of angular speeds of the cars will be \(1: 1\).
-
Question 85 of 86
85. Question
The ratio of the distances travelled by a freely falling body in the \(1^{\text {st }}, 2^{\text {nd }}, 3^{\text {rd }}\) and \(4^{\text {th }}\) second [NEET 2022]
CorrectIncorrectHint
\(
\begin{aligned}
& S_{n^{t h}}=u+\frac{1}{2} a(2 n-1) \\
& S_{1^{s t}}=\frac{1}{2} g(2 \times 1-1)=\frac{g}{2} \\
& S_{2^{n d}}=\frac{1}{2} g(2 \times 2-1)=3\left(\frac{1}{2} g\right)
\end{aligned}
\)
\(
\begin{aligned}
& S_{3^{\text {rd }}}=\frac{1}{2} g(2 \times 3-1)=5 \times\left(\frac{1}{2} g\right) \\
& S_{4^{\text {th }}}=\frac{1}{2} g(2 \times 4-1)=7 \times\left(\frac{1}{2} g\right) \\
& S_{1^{s t}}: S_{2^{\text {nd }}}: S_{3^{\text {rd }}}: S_{4^{\text {th }}} \\
& =1: 3: 5: 7
\end{aligned}
\) -
Question 86 of 86
86. Question
Calculate the maximum acceleration of a moving car so that a body lying on the floor of the car remains stationary. The coefficient of static friction between the body and the floor is \(0.15\left(g=10 \mathrm{~m} \mathrm{~s}^{-2}\right)\). [NEET 2023]
CorrectIncorrectHint
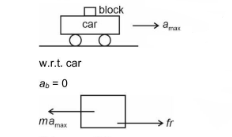
\(
\begin{aligned}
& m a_{\max }=\mu_s m g \\
& a_{\max }=\mu_s g=0.15 \times 10=1.5 \mathrm{~m} / \mathrm{s}^2
\end{aligned}
\)