Sample Exercises
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
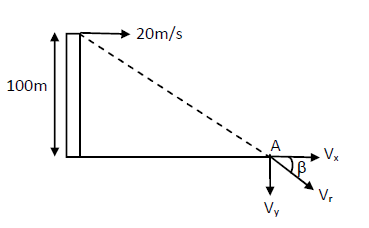
A ball is thrown horizontally from a point \(100 \mathrm{~m}\) above the ground with a speed of \(20 \mathrm{~m} / \mathrm{s}\). Find (a) the time it takes to reach the ground, (b) the horizontal distance it travels before reaching the ground, and (c) the velocity (direction and magnitude) with which it strikes the ground.
CorrectIncorrectHint
Given,
\(
\mathrm{h}=100 \mathrm{~m}, \mathrm{v}=20 \mathrm{~m} / \mathrm{s}, \mathrm{g}=9.8 \mathrm{~m} / \mathrm{s}^{2}
\)
This shows projectile,
a) time it takes to reach the ground,
\(
\begin{aligned}
&\mathrm{t}=\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}} \\
&=\sqrt{\frac{2 \times 100}{9.8}}=4.51 \mathrm{~s}
\end{aligned}
\)
b) The horizontal distance traveled before reaching the ground,
\(
\begin{aligned}
&x=u t \\
&=20 \times 4.5=90 \mathrm{~m}
\end{aligned}
\)c) Horizontal velocity remains constant throughout the frequency,
At “A”, \(\mathrm{V}_{\mathrm{x}}=20 \mathrm{~m} / \mathrm{s}, \mathrm{V}_{\mathrm{y}}=\mathrm{u}+\) at \(=0+9.8 \times 4.5=44.1 \mathrm{~m} / \mathrm{s}\)
Final velocity
\(
=\mathrm{v}_{\mathrm{r}}=\sqrt{(4.41)^{2}+(20)^{2}}=48.42 \mathrm{~m} / \mathrm{s}
\)
\(
\tan \beta=\frac{\mathrm{V}_{\mathrm{y}}}{\sqrt{\mathrm{x}}}=\frac{4.41}{20}=2.205
\)
\(
\Rightarrow \beta=\tan ^{-1} 2.205=66^{\circ}
\)
-
Question 2 of 50
2. Question
A ball is thrown at a speed of \(40 \mathrm{~m} / \mathrm{s}\) at an angle of \(60^{\circ}\) with the horizontal. Find (a) the maximum height reached and (b) the range of the ball. Take \(g=10 \mathrm{~m} / \mathrm{s}^{2}\).
CorrectIncorrectHint
Given \(\mathrm{u}=40 \mathrm{~m} / \mathrm{s}, \theta=60^{\circ}\) and \(g=10 \mathrm{~m} / \mathrm{s}^{2}\)
Maximum Height \(\mathrm{h}_{\mathrm{m}}=\frac{\mathrm{u}^{2} \sin ^{2} \theta}{2 \mathrm{~g}}=60 \mathrm{~m}\)
Range \(\mathrm{R}=\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}=80 \sqrt[2]{3} \mathrm{~m}\) -
Question 3 of 50
3. Question
In a soccer practice session, the football is kept at the centre of the field 40 yards from the \(10 \mathrm{ft}\) high goalposts. A goal is attempted by kicking the football at a speed of \(64 \mathrm{ft} / \mathrm{s}\) at an angle of \(45^{\circ}\) to the horizontal. Will the ball reach the goal post?
CorrectIncorrectHint
The acceleration due to gravity on earth is \(g=9.8 \mathrm{~m} / \mathrm{s}^{2} = 32.2 \mathrm{~ft} / \mathrm{s}^{2}\)
We know that 40 yards \(=120\) feet
Horizontal range \(\mathrm{x}=120 \mathrm{ft}\)
The initial speed of the ball is \(\mathrm{u}=64 \mathrm{ft} / \mathrm{s}\)
The angle at which the ball is kicked \(\theta=45^{\circ}\)
know that horizontal range \(x=u \cos \theta t\)
\(t=\frac{x}{u \cos \theta}\)
\(t=\frac{120}{64 \cos 45^{0}}\)
\(t=\frac{120}{64 \times \frac{1}{\sqrt{2}}}\)
\(
=\frac{120 \times 1.414}{64}
\)
\(
=2.65 \mathrm{sec}
\)\(
y=u \sin \theta(t)-1 / 2 g{t}^{2}=64 \frac{1}{\sqrt{2}(2.65)}-\frac{1}{2}(32.2)(2.65)^{2}
\)
\(=7.08 \mathrm{ft}\) which is less than the height of goal post.
In time \(2.65\), the ball travels horizontal distance \(120 \mathrm{ft}(40 \mathrm{yd})\) and vertical height \(7.08 \mathrm{ft}\) which is less than \(10 \mathrm{ft}\). The ball will reach the goal post. -
Question 4 of 50
4. Question
A popular game in Indian villages is goli which is played with small glass balls called golis. The goli of one player is situated at a distance of \(2.0 \mathrm{~m}\) from the goli of the second player. This second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middle fingers and making the throw. If the projected goli hits the goli of the first player, the second player wins. If the height from which the goli is projected is \(19.6 \mathrm{~cm}\) from the ground and the goli is to be projected horizontally, with what speed should it be projected so that it directly hits the stationary goli without falling on the ground earlier?
CorrectIncorrectHint
Goli moves like a projectile.
\(
\mathrm{h}=19.6 \mathrm{~cm}=0.196 \mathrm{~m}
\)
Horizontal distance \(\mathrm{x}=2 \mathrm{~m}\)
Time to reach the ground \(=\mathrm{t}=\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}=\frac{2 \times 0.196}{9.8}=0.2 \mathrm{sec}\)
Let the horizontal velocity with which the goli is to be projected be u
\(
\mathrm{u}=\mathrm{x} / \mathrm{t}=\frac{2 \mathrm{~m}}{0.2 \mathrm{~s}}=10 \mathrm{~m} / \mathrm{s}
\) -
Question 5 of 50
5. Question
The figure below shows a \(11.7 \mathrm{ft}\) wide ditch with the approach roads at an angle of \(15^{\circ}\) with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch? Assume that the length of the bike is \(5 \mathrm{ft}\), and it leaves the road when the front part runs out of the approach road.
 CorrectIncorrect
CorrectIncorrectHint
Width of the ditch \(=11.7 \mathrm{ft}\)
Length of the bike \(=5 \mathrm{ft}\)
The approach road makes an angle of \(15^{\circ}(\theta)\) with the horizontal.
Total horizontal range that should be covered by the biker to cross the ditch safely, \(R=11.7+5=16.7 \mathrm{ft}\)
Acceleration due to gravity, \(a=g=9.8 \mathrm{~m} / \mathrm{s}=32.2 \mathrm{ft} / \mathrm{s}^{2}\)
We know that the horizontal range is given by
\(R=\frac{u^{2} \sin 2 \theta}{g}\)
By putting respective values, we get:
\(
\begin{aligned}
&u^{2}=\frac{R g}{\sin 2 \theta}=\frac{16.7 \times 32.2}{\sin 30^{\circ}} \\
&\Rightarrow u \approx 32 f t / s
\end{aligned}
\)
Therefore, the minimum speed with which the motorbike should be moving is \(32 \mathrm{ft} / \mathrm{s}\).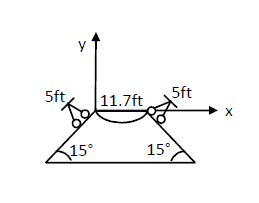
-
Question 6 of 50
6. Question
A person standing on the top of a cliff \(171 \mathrm{ft}\) high has to throw a packet to his friend standing on the ground 228 ft horizontally away. If he throws the packet directly aiming at the friend with a speed of \(15.0 \mathrm{ft} / \mathrm{s}\), how short will the packet fall?
CorrectIncorrectHint
Given:
Height (h) of the cliff \(=171 \mathrm{ft}\)
Horizontal distance from the bottom of the cliff \(=228 \mathrm{ft}\)
As per the question, the person throws the packet directly aiming to his friend at the initial speed (u) of \(15.0 \mathrm{ft} / \mathrm{s}\).From the diagram, we can write:
\(
\begin{aligned}
&\tan \theta=\frac{171}{228} \\
&\Rightarrow \theta=\tan ^{-1}\left(\frac{171}{228}\right) \\
&\therefore \theta=37^{\circ}
\end{aligned}
\)
When the person throws the packet from the top of the cliff, it moves in projectile motion.
\(a=g=32.2 \mathrm{ft} / \mathrm{s}^{2}\) (Acceleration due to gravity)
Using the second equation of motion, we get:
\(
\begin{aligned}
&y=u \sin \theta t+\frac{1}{2} g t^{2} \\
&y=171 f t \\
&\theta=37^{\circ}
\end{aligned}
\)\(
\begin{aligned}
&g=32 f t / s^{2} \\
&T=\text { Time of flight } \\
&171=15 \sin (37) t+\frac{1}{2} \times 32 \times t^{2}
\end{aligned}
\)
On solving this quadratic equation in \(\mathrm{t}\), we get:
\(
\begin{aligned}
&t=2.99 \mathrm{~s} \\
&\text { Range }=15 \cos (37) \times 2.99=35.81 \mathrm{ft}
\end{aligned}
\)
Distance by which the packet will fall short \(=228-35.81=192 \mathrm{ft}\)(approx.)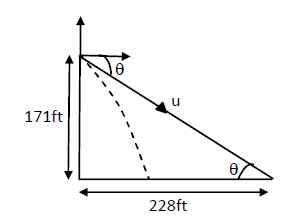
-
Question 7 of 50
7. Question
A ball is projected from a point on the floor with a speed of \(15 \mathrm{~m} / \mathrm{s}\) at an angle of \(60^{\circ}\) with the horizontal. Will it hit a vertical wall \(5 \mathrm{~m}\) away from the point of projection and perpendicular to the plane of projection without hitting the floor? Will the answer differ if the wall is \(22 \mathrm{~m}\) away?
CorrectIncorrectHint
Here,
\(
\begin{aligned}
\mathrm{u} &=15 \mathrm{~m} / \mathrm{s} \\
\theta &=60^{\circ} \\
\mathrm{g} &=9.8 \mathrm{~m} / \mathrm{s}^{2}
\end{aligned}
\)
Formula for range of the ball
\(
\mathrm{x}=\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}
\)
\(
=\frac{15^{2} \sin 2 \times 60}{9.8}
\)
\(
=\frac{225 \sin 120}{9.8}
\)
\(
\therefore \mathrm{x}=19.8 \mathrm{~m}
\)
So in case-1, the wall is \(5 \mathrm{~m}\) away from the projection point so it is in the horizontal range of the projectile. So the ball will hit the wall.In case-2, \(22 \mathrm{~m}\) away the wall is not within the horizontal range. So the ball would not hit the wall.
-
Question 8 of 50
8. Question
Find the average velocity of a projectile between the instants it crosses half the maximum height. It is projected with a speed \(u\) at an angle \(\theta\) with the horizontal.
CorrectIncorrectHint
Given:
The initial velocity of the projectile \(=u\)
The angle of projection \(=\theta\)
To find: Average velocity of the projectile
Average velocity
\(=\frac{\text { Change in displacement }}{\text { Time }}\)
Consider the projectile motion in the figure given below.
By the symmetry of the figure, it can be said that the line joining points \(A\) and \(B\) is horizontal.
So, there will be no effect on the vertical component of velocity of the projectile during displacement \(A B\).
We know that the projectile moves at a constant velocity \(u \cos \theta\) in the horizontal direction.
Hence, the average velocity of the projectile is \(u \cos \theta\).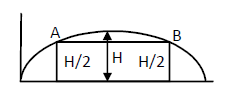
-
Question 9 of 50
9. Question
A boy standing on a long railroad car throws a ball straight upwards. The car is moving on the horizontal road with an acceleration of \(1 \mathrm{~m} / \mathrm{s}^{2}\) and the projection velocity in the vertical direction is \(9.8 \mathrm{~m} / \mathrm{s}\). How far behind the boy will the ball fall on the car?
CorrectIncorrectHint
Given:
Acceleration of the car \(=1 \mathrm{~m} / \mathrm{s}^{2}\)
Projection velocity of the ball (considered as a projectile) in the vertical direction \(=9.8 \mathrm{~m} / \mathrm{s}\)
Angle of projection, \(\theta=90^{\circ}\)
Let \(u\) be the initial velocity of the car when the ball is thrown.
Both the car and the ball have the same horizontal velocity.Initial velocity of car is = Horizontal velocity of ball.
Distance travelled by ball \( S_{b}=u t\) (in horizontal direction)
and also the distanced travelled by the car in horizontal direction \(S_{c}=u t+1 / 2\) at \({ }^{2}\) where \(t \rightarrow\) time of flight of ball in air.
\(\therefore\) Car has travelled extra distance \(\mathrm{S}_{\mathrm{c}}-\mathrm{S}_{\mathrm{b}}=1 / 2 \mathrm{at}^{2}\).
Ball can be considered as a projectile having \(\theta=90^{\circ}\).
\(\therefore t=\frac{2 \mathrm{u} \sin \theta}{\mathrm{g}}=\frac{2 \times 9.8}{9.8}=2 \mathrm{sec}\).
\(
\therefore \mathrm{S}_{\mathrm{c}}-\mathrm{S}_{\mathrm{b}}=1 / 2 \mathrm{at}^{2}=2 \mathrm{~m}
\)
\(\therefore\) The ball will drop \(2 \mathrm{~m}\) behind the boy. -
Question 10 of 50
10. Question
A staircase contains three steps each \(10 \mathrm{~cm}\) high and \(20 \mathrm{~cm}\) wide shown in figure below. What should be the minimum horizontal velocity of a ball rolling off the uppermost plane so as to hit directly the lowest plane?
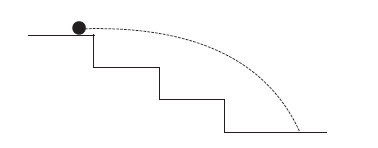 CorrectIncorrect
CorrectIncorrectHint
To directly hit the lowest plane, the ball should just touch point E.
Let point A be the origin of reference coordinate. Let \(u\) be the minimum speed of the ball.
We have:
\(
\begin{aligned}
&x=40 \mathrm{~cm} \\
&y=-20 \mathrm{~cm} \\
&\theta=0^{\circ} \\
&g=10 \mathrm{~m} / \mathrm{s}^{2}=1000 \mathrm{~cm} / \mathrm{s}^{2} \\
&\therefore y=x \tan \theta-g \frac{x^{2} \sec ^{2} \theta}{2 u^{2}} \\
&\Rightarrow-20=-\frac{800000}{2 u^{2}} \\
&\Rightarrow u=200 \mathrm{~cm} / \mathrm{s}=2 \mathrm{~m} / \mathrm{s}
\end{aligned}
\)
Thus, the minimum horizontal velocity of the ball is \(2 \mathrm{~m} / \mathrm{s}\).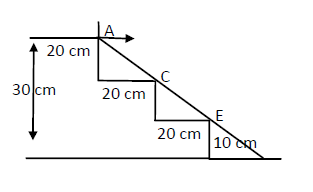
-
Question 11 of 50
11. Question
A person is standing on a truck moving with a constant velocity of \(14.7 \mathrm{~m} / \mathrm{s}\) on a horizontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved \(58.8 \mathrm{~m}\). Find the speed and the angle of projection (a) as seen from the truck, (b) as seen from the road.
CorrectIncorrectHint
Velocity of truck \(\mathrm{v}_{\mathrm{t}}=14.7 \mathrm{~m} / \mathrm{s}\)
Distance \(\mathrm{s}=58.8 \mathrm{~m}\)
(a) As seen from the truck the ball moves vertically upward and comes back. Time taken is equal to the time taken by truck to cover \(58.8 \mathrm{~m}\). Therefore angle of projection as seen from the truck \(=90^{\circ}\)Time taken by the truck, \(\text {t}=\frac{\mathrm{s}}{\mathrm{v_{t}}}=\frac{58.8}{14.7}=4 \mathrm{~s}\)
\(
\begin{aligned}
&\mathrm{t}=\frac{2 \mathrm{u} \sin \theta}{\mathrm{g}} \\
&\mathrm{u}=\frac{\operatorname{tg}}{2 \sin \theta}=\frac{4 \times 9.8}{2 \times 1}=2 \times 9.8=19.6 \mathrm{~m} / \mathrm{s}
\end{aligned}
\)(b) b) From the road it seems to be projectile motion.
Total time of flight \(=4 \mathrm{sec}\)
In this time horizontal range covered \(58.8 \mathrm{~m}=\mathrm{x}\)
\(
\begin{aligned}
&\therefore \mathrm{x}=\mathrm{u} \cos \theta \mathrm{t} \\
&\Rightarrow \mathrm{u} \cos \theta=14.7
\end{aligned}
\)
Taking the vertical component of velocity into consideration.
\(\begin{aligned} y=\frac{0^{2}-(19.6)^{2}}{2 \times(-9.8)}=19.6 \mathrm{~m}[\text { from }(\mathrm{a})] \\ \therefore \mathrm{y}=\mathrm{u} \sin \theta \mathrm{t}-1 / 2 \mathrm{gt}^{2} \\ \Rightarrow 19.6=\mathrm{u} \sin \theta(2)-1 / 2(9.8) 2^{2} \Rightarrow 2 \mathrm{u} \sin \theta=19.6 \times 2 \\ \Rightarrow \mathrm{u} \sin \theta=19.6 \\ \frac{\mathrm{u} \sin \theta}{\mathrm{u} \cos \theta}=\tan \theta \Rightarrow \frac{19.6}{14.7}=1.333 \\ \Rightarrow \theta=\tan ^{-1}(1.333)=53^{\circ} \\ \text { Again } u \cos \theta=14.7 \\ \Rightarrow u=\frac{14.7}{u \cos 53^{\circ}}=24.42 \mathrm{~m} / \mathrm{s} . \end{aligned}\)
The speed of ball is \(42.42 \mathrm{~m} / \mathrm{s}\) at an angle \(53^{\circ}\) with horizontal as seen from the road. -
Question 12 of 50
12. Question
The benches of a gallery in a cricket stadium are \(1 \mathrm{~m}\) wide and \(1 \mathrm{~m}\) high. A batsman strikes the ball at a level one meter above the ground and hits a mammoth sixer. The ball starts at \(35 \mathrm{~m} / \mathrm{s}\) at an angle of \(53^{\circ}\) with the horizontal. The benches are perpendicular to the plane of motion and the first bench is \(110 \mathrm{~m}\) from the batsman. On which bench will the ball hit?
CorrectIncorrectHint
Given:
The angle of projection of the ball, \(\theta=53^{\circ}\)
Width and height of the bench \(=1 \mathrm{~m}\)
Initial speed of the ball \(=35 \mathrm{~m} / \mathrm{s}\)
Distance of the first bench from the batsman \(=110 \mathrm{~m}\)
The batsman strikes the ball \(1 \mathrm{~m}\) above the ground.
Let the ball land on the \(\mathrm{n}^{\text {th }}\) bench.
\(
\therefore y=(n-1) \quad \ldots(\mathrm{i})
\)
and,
\(
x=110+n-1=110+y
\)Now ,
\(y=x \tan \theta-\left(\frac{g x^{2} \sec ^{2} \alpha}{2 u^{2}}\right)\) \(\Rightarrow y=(110+y)\left(\frac{4}{3}\right)-\frac{10 \times(110+y)^{2}\left(\sec ^{2} 53^{\circ}\right)}{2 \times(35)^{2}}\) \(=\frac{440}{3}+\frac{4}{3} y-\frac{250(110+y)^{2}}{18 \times(35)^{2}}\) \(=\frac{440}{3}+\frac{4}{3} y-\frac{250(110+y)^{2}}{18 \times 35^{2}}\)Solving the above equation, we get: \(y=5\) \(\Rightarrow\) n -1=5 \(\Rightarrow\) n \(=6\)
The ball will hit the sixth bench of the gallery.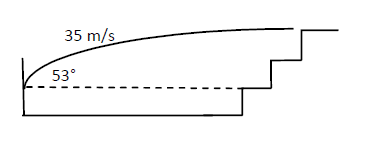
-
Question 13 of 50
13. Question
A man is sitting on the shore of a river. He is in the line of a \(1.0 \mathrm{~m}\) long boat and is \(5.5 \mathrm{~m}\) away from the centre of the boat. He wishes to throw an apple into the boat. If he can throw the apple only with a speed of 10 \(\mathrm{m} / \mathrm{s}\), find the minimum and maximum angles of projection for a successful shot. Assume that the point of projection and the edge of the boat is in the same horizontal level.
CorrectIncorrectHint
Length of the boat \(=1.0 \mathrm{~m}\)
Distance between the man and the centre of the boat \((R)=5.5 \mathrm{~m}\)
Initial speed (u) of throwing the apple by the man \(=10 \mathrm{~m} / \mathrm{s}\)
Acceleration due to gravity \((\mathrm{g})=10 \mathrm{~m} / \mathrm{s}^{2}\)
We know that the horizontal range is given by
\(\begin{aligned}
&R=\frac{u^{2} \sin 2 \theta}{g} \\
&\Rightarrow 5=\frac{(10)^{2} \sin 2 \theta}{10} \\
&\Rightarrow \sin 2 \theta=\frac{1}{2} \\
&\Rightarrow \theta=15^{\circ} \text { or } 75^{\circ}
\end{aligned}\)Similarly, for the endpoint of the boat, we have:
Horizontal range \((R)=6 \mathrm{~m}\)
\(
\begin{aligned}
&R=\frac{u^{2} \sin 2 \theta}{g} \\
&\Rightarrow 6=\frac{(10)^{2} \sin 2 \theta}{10} \\
&\Rightarrow \sin 2 \theta=\frac{3}{5} \\
&\Rightarrow \theta=18^{\circ} \text { or } 71^{\circ}
\end{aligned}
\)
For a successful shot, the angle of projection \(\theta\) with initial speed \(10 \mathrm{~m} / \mathrm{s}\) may vary from \(15^{\circ}\) to \(18^{\circ}\) or from \(71^{\circ}\) to \(75^{\circ}\). The minimum angle is \(15^{\circ}\) and the maximum angle is \(75^{\circ}\).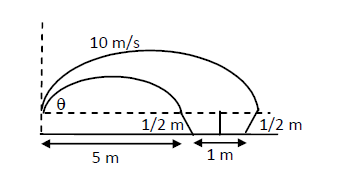
-
Question 14 of 50
14. Question
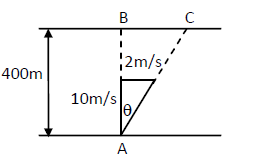
A river \(400 \mathrm{~m}\) wide is flowing at a rate of \(2.0 \mathrm{~m} / \mathrm{s} .\) A boat is sailing at a velocity of \(10 \mathrm{~m} / \mathrm{s}\) with respect to the water, in a direction perpendicular to the river. (a) Find the time taken by the boat to reach the opposite bank. (b) How far from the point directly opposite to the starting point does the boat reach the opposite bank?
CorrectIncorrectHint
a) Here the boat moves with the resultant velocity \(V_{r}\). But the vertical component \(10 \mathrm{~m} / \mathrm{s}\) takes him to the opposite shore.
\(\operatorname{tan} \theta=2 / 10=1 / 5\)
Velocity \(=10 \mathrm{~m} / \mathrm{s}\)
distance \(=400 \mathrm{~m}\)
Time \(=400 / 10=40 \mathrm{sec}\).
b) The boat will reach at point \(C\).
\(
\begin{aligned}
& \text { In } \triangle A B C, \tan \theta=\frac{B C}{A B}=\frac{B C}{400}=\frac{1}{5} \\
\Rightarrow & B C=400 / 5=80 \mathrm{~m} .
\end{aligned}
\)
-
Question 15 of 50
15. Question
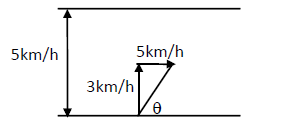
A swimmer wishes to cross a \(500 \mathrm{~m}\) wide river flowing at \(5 \mathrm{~km} / \mathrm{h}\). His speed with respect to water is \(3 \mathrm{~km} / \mathrm{h}\). (a) If he heads in a direction making an angle \(\theta\) with the flow, find the time he takes to cross the river. (b) Find the shortest possible time to cross the river.
CorrectIncorrectHint
(a) Width of the river \(=500 \mathrm{~m}\)
Rate of flow of the river \(=5 \mathrm{~km} / \mathrm{h}\)
Swimmer’s speed with respect to water \(=3 \mathrm{~km} / \mathrm{h}\)
As per the question, the swimmer heads in a direction making an angle \(\theta\) with the flow.
We know that the vertical component of velocity \(3 \sin \theta\) takes him to the opposite side of the river.
Distance to be travelled \(=0.5 \mathrm{~km}\)
Vertical component of velocity \(=3 \sin \theta \mathrm{km} / \mathrm{h}\)
Thus, we have:
\(
\text { Time }=\frac{\text { Distance }}{\text { Velocity }}=\frac{0.5}{3 \sin \theta} h=\frac{500 \times 6}{5 \sin \theta}=\frac{600}{\sin \theta} s
\)
\(\therefore\) Required time \(=\frac{10}{\sin \theta}\) minute.(b) Here vertical component of velocity i.e. \(3 \mathrm{~km} / \mathrm{hr}\) takes him to opposite side Time \(=\frac{\text { Distance }}{\text { Velocity }}=\frac{0.5}{3}=0.16 \mathrm{hr}\)
\(5 \mathrm{~km} / \mathrm{h}\)
\(
\therefore 0.16 \mathrm{hr}=60 \times 0.16=9.6=10 \text { minute. }
\)
-
Question 16 of 50
16. Question
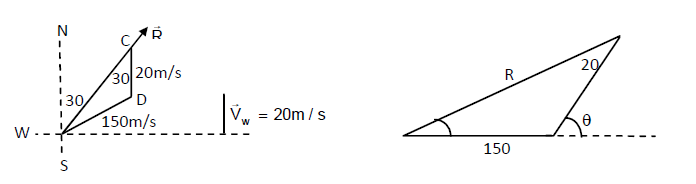
An aeroplane has to go from a point A to another point B, \( 500 \mathrm{~km}\) away due \(30^{\circ}\) east of north. A wind is blowing due north at a speed of \(20 \mathrm{~m} / \mathrm{s}\). The air-speed of the plane is \(150 \mathrm{~m} / \mathrm{s}\). (a) Find the direction in which the pilot should head the plane to reach point B. (b) Find the time taken by the plane to go from A to B.
CorrectIncorrectHint
Distance between points A and B=\(500 \mathrm{~km}\)
B from A is \(30^{\circ}\) east of north.
Speed of wind due north, \(V_{w}=20 \mathrm{~m} / \mathrm{s}\)
Velocity of aeroplane is, \(V_{a}=150 \mathrm{~m} / \mathrm{s}\)
Let \(\vec{R}\) be the resultant direction of the plane to reach point B.In \(\triangle A C D\) according to the sine formula
\(
\begin{aligned}
&\therefore \frac{20}{\sin A}=\frac{150}{\sin 30^{\circ}} \Rightarrow \sin A=\frac{20}{150} \sin 30^{\circ}=\frac{1}{15} \\
&\Rightarrow A=\sin ^{-1}(1 / 15)
\end{aligned}
\)
a) The direction is \(\sin ^{-1}(1 / 15)\) east of the line AB.
b) \(\sin ^{-1}(1 / 15)=3^{\circ} 48^{\prime}\)
\(
\begin{aligned}
&\Rightarrow 30^{\circ}+3^{\circ} 48^{\prime}=33^{\circ} 48^{\prime} \\
&R=\sqrt{150^{2}+20^{2}+2(150) 20 \cos 33^{\circ} 48^{\prime}}=167 \mathrm{~m} / \mathrm{s} . \\
&\text { Time }=\frac{\mathrm{s}}{\mathrm{v}}=\frac{500000}{167}=2994 \mathrm{sec}=50 \mathrm{~min} (approx.).
\end{aligned}
\)
-
Question 17 of 50
17. Question
Two friends A and B are standing a distance \(x\) apart in an open field and the wind is blowing from A to B. A beats a drum and B hears the sound \(t_{1}\) time after he sees the event. A and B interchange their positions and the experiment is repeated. This time B hears the drum \(t_{2}\) time after he sees the event. Calculate the velocity of sound in still air \(v\) and the velocity of wind \(u\). Neglect the time light takes in travelling between the friends.
CorrectIncorrectHint
The velocity of sound \(v\), Velocity of air \(u\), Distance between A and B be \(x\).
In the first case, the resultant velocity of sound \(=v+u\)
\(
\begin{aligned}
&\Rightarrow(v+u) t_{1}=x \\
&\Rightarrow v+u=x / t_{1} \quad \text {…(1) }
\end{aligned}
\)
In the second case, resultant velocity of sound \(=v-u\)\(\begin{aligned}
&\therefore(v-u) t_{2}=x \\
&\Rightarrow v-u=x / t_{2}\quad \text {…(2) }
\end{aligned}\)
From (1) and (2) \( 2 v=\frac{x}{t_{1}}+\frac{x}{t_{2}}=x\left(\frac{1}{t_{1}}+\frac{1}{t_{2}}\right)\)
\(
\Rightarrow v=\frac{x}{2}\left(\frac{1}{t_{1}}+\frac{1}{t_{2}}\right)
\)
From (i) \(u=\frac{x}{t_{1}}-v=\frac{x}{t_{1}}-\left(\frac{x}{2 t_{1}}+\frac{x}{2 t_{2}}\right)=\frac{x}{2}\left(\frac{1}{t_{1}}-\frac{1}{t_{2}}\right)\)
\(\therefore\) Velocity of air \(v=\frac{x}{2}\left(\frac{1}{t_{1}}+\frac{1}{t_{2}}\right)\)
And velocity of wind \(u=\frac{x}{2}\left(\frac{1}{t_{1}}-\frac{1}{t_{2}}\right)\) -
Question 18 of 50
18. Question
Six particles situated at the corners of a regular hexagon of side \(a\) move at a constant speed \(v\). Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
CorrectIncorrectHint
As per the question, each particle maintains a direction towards the particle at the next corner. So, particles will meet at centroid \(O\) of triangle ABC. Now, at any instant, the particles will form an equilateral triangle \(B A C\) with the same centroid \(O\). We know that \(B\) approaches \(A\), \(A\) approaches \(C\) and so on.
Now, we will consider the motion of particle B. Its velocity makes an angle of \(60^{\circ}\).
This component is the rate of decrease of distance BO.
Relative velocity between \(\mathrm{B}\) and \(\mathrm{A}\):\(
\mathrm{v}_{\mathrm{r}}=\mathrm{v}-\mathrm{v} \cos 60^{\circ}=\mathrm{v}-\frac{\mathrm{v}}{2}=\frac{\mathrm{v}}{2}\)
Relative velocity = Total displacement/Time taken
\(
\begin{aligned}
&\Rightarrow \frac{\mathrm{v}}{2}=\frac{\mathrm{a}}{\mathrm{t}} \\
&\Rightarrow \mathrm{t}=\frac{2 \mathrm{a}}{\mathrm{v}}
\end{aligned}
\)
Hence, the time taken by the particles to meet each other is \(\frac{2 \mathrm{a}}{\mathrm{v}}\)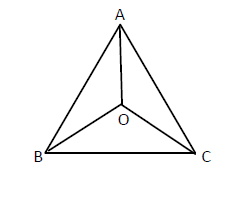
-
Question 19 of 50
19. Question
Three girls skating on a circular ice ground of radius \(200 \mathrm{~m}\) start from a point \(P\) on the edge of the ground and reach a point \(Q\) diametrically opposite to \(P\) following different paths as shown in Figure below. What is the magnitude of the displacement vector for each? For which girl is this equal to the actual length of path skate?
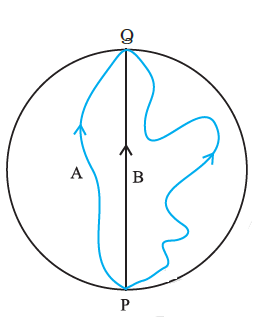 CorrectIncorrect
CorrectIncorrectHint
Displacement is given by the minimum distance between the initial and final positions of a particle. In the given case, all the girls start from point \(P\) and reach point \(Q\). The magnitudes of their displacements will be equal to the diameter of the ground.
Radius of the ground \(=200 \mathrm{~m}\)
Diameter of the ground \(=2 \times 200=400 \mathrm{~m}\)
Hence, the magnitude of the displacement for each girl is \(400 \mathrm{~m}\). This is equal to the actual length of the path skated by girl B. -
Question 20 of 50
20. Question
A cyclist starts from the centre O of a circular park of radius \(1 \mathrm{~km}\), reaches the edge P of the park, then cycles along the circumference, and returns to the centre along QO as shown in Figure below. If the round trip takes \(10 \mathrm{~min}\), what is the (a) net displacement, (b) average velocity, and (c) average speed of the cyclist?
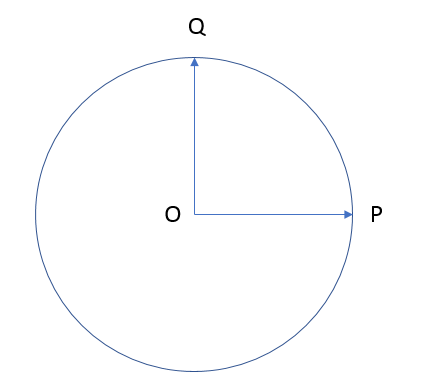 CorrectIncorrect
CorrectIncorrectHint
(a) Displacement is given by the minimum distance between the initial and final positions of a body. In the given case, the cyclist comes to the starting point after cycling for 10 minutes. Hence, his net displacement is zero.
(b) Average velocity is given by the relation:
Average velocity \(=\frac{\text { Net displacement }}{\text { Total time }}\)
Since the net displacement of the cyclist is zero, his average velocity will also be zero.(c) Average speed of the cyclist is given by the relation:
Average speed \(=\frac{\text { Total path length }}{\text { Total time }}\)
Total path length \(=O P+P Q+Q O\)
\(
\begin{aligned}
&=1+\frac{1}{4}(2 \pi \times 1)+1 \\
&=2+\frac{1}{2} \pi=3.570 \mathrm{~km}
\end{aligned}
\)
Time taken \(=10 \mathrm{~min}=\frac{10}{60}=\frac{1}{6} h\)
\(\therefore\) Average speed \(=\frac{3.570}{\frac{1}{6}}=21.42 \mathrm{~km} / \mathrm{h}\) -
Question 21 of 50
21. Question
On an open ground, a motorist follows a track that turns to his left by an angle of \(60^{\circ}\) after every \(500 \mathrm{~m}\). Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn.
CorrectIncorrectHint
The path followed by the motorist is a regular hexagon with side \(500 \mathrm{~m}\), as shown in the given figure. Let the motorist start from point A. The motorist takes the third turn at D. Magnitude of displacement \(=\mathrm{AD}=\mathrm{BC}+\mathrm{EF}=500+500=1000 \mathrm{~m}\). Total path length \(=\mathrm{AB}+\mathrm{BC}+\mathrm{CD}=500+500+500=1500 \mathrm{~m}\). The motorist takes the sixth turn at point A, which is the starting point. Magnitude of displacement =0. Total path length \(=6 \mathrm{AB}\)
\( =6 \times 500=3000 \mathrm{~m}\)
The motorist takes the eight turn at point C
The magnitude of displacement \(=\mathrm{AC}\)
From triangle law, the magnitude of displacement is \(866.03 \mathrm{~m}\) at an angle of \(30^{\circ}\) with \(\mathrm{AC}\). It means AC makes an angle of \(30^{\circ}\) with the initial direction. Total path length = \(8 \times 500=4000 \mathrm{~m}\).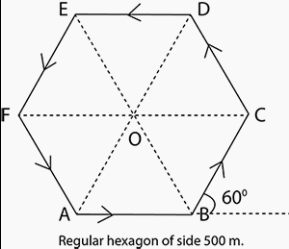
-
Question 22 of 50
22. Question
Rain is falling vertically with a speed of \(30 \mathrm{~m} \mathrm{~s}^{-1}\). A woman rides a bicycle with a speed of \(10 \mathrm{~m} \mathrm{~s}^{-1}\) in the north to south direction. What is the direction in which she should hold her umbrella?
CorrectIncorrectHint
Here,
\(v_{c}=\) Velocity of the cyclist
\(v_{r}=\) Velocity of falling rain
In order to protect herself from the rain, the woman must hold her umbrella in the direction of the relative velocity \((v)\) of the rain with respect to the woman.
\(\vec{v}=\overrightarrow{v_{r}}+\left(-\vec{v}_{c}\right)\)
Resultant, \(|v|=\sqrt{v_{r^{2}}+v_{c^{2}}}\)
\(|v|=\sqrt{30^{2}+10^{2}}\)
\(|v|=\sqrt{900+100}\)
\(|v|=\sqrt{1000}=10 \sqrt{10} m\)
\(\tan \theta=\frac{v_{c}}{v_{r}}=\frac{10}{30}\)
\(\theta=\tan ^{-1}\left(\frac{1}{3}\right)\)
\(\theta=\tan ^{-1}(0.333) \approx 18^{\circ}\)Hence, the woman must hold the umbrella toward the south, at an angle of nearly \(18^{\circ}\)
-
Question 23 of 50
23. Question
A man can swim with a speed of \(4.0 \mathrm{~km} / \mathrm{h}\) in still water. How long does he take to cross a river \(1.0 \mathrm{~km}\) wide if the river flows steadily at \(3.0 \mathrm{~km} / \mathrm{h}\) and he makes his strokes normal to the river current? How far down the river does he go when he reaches the other bank?
CorrectIncorrectHint
Speed of the man, \(v_{\mathrm{m}}=4 \mathrm{~km} / \mathrm{h}\)
Width of the river \(=1 \mathrm{~km}\)
Time taken to cross the river \(=\frac{\text { Width of river }}{\text { Speed of man }}\) \(=\frac{1}{4} h=\frac{1}{4} \times 60=15 \mathrm{~min}\)
Speed of the river, \(v_{r}=3 \mathrm{~km} / \mathrm{h}\)
Distance covered with flow of the river \(=v_{r} \times t\)
\(
\begin{aligned}
&=3 \times \frac{1}{4}=\frac{3}{4} k m \\
&=\frac{3}{4} \times 1000=750 m
\end{aligned}
\) -
Question 24 of 50
24. Question
In a harbour, wind is blowing at the speed of \(72 \mathrm{~km} / \mathrm{h}\), and the flag on the mast of a boat anchored in the harbor flutters along the \(\mathrm{N}-\mathrm{E}\) direction. If the boat starts moving at a speed of \(51 \mathrm{~km} / \mathrm{h}\) to the north, what is the direction of the flag on the mast of the boat?
CorrectIncorrectHint
Velocity of the boat, \(v_{\mathrm{b}}=51 \mathrm{~km} / \mathrm{h}\)
Velocity of the wind, \(v_{\mathrm{w}}=72 \mathrm{~km} / \mathrm{h}\)
The flag is fluttering in the north-east direction. It shows that the wind is blowing toward the north-east direction. When the ship begins sailing toward the north, the flag will move along the direction of the relative velocity \(\left(v_{w b}\right)\) of the wind with respect to the boat. The angle between \(v_{\mathrm{w}}\) and \(\left(-v_{\mathrm{b}}\right)=90^{\circ}+45^{\circ}\)
\(
\begin{aligned}
&\tan \beta=\frac{51 \sin (90+45)}{72+51 \cos (90+45)} \\
&=\frac{51 \sin 45}{72+51(-\cos 45)}=\frac{51 \times \frac{1}{\sqrt{2}}}{72-51 \times \frac{1}{\sqrt{2}}} \\
&=\frac{51}{72 \sqrt{2}-51}=\frac{51}{72 \times 1.414-51}=\frac{51}{50.800} \\
&\therefore \beta=\tan ^{-1}(1.0038)=45.11^{\circ}
\end{aligned}
\)
Angle with respect to the east direction \(=45.11^{\circ}-45^{\circ}=0.11^{\circ}\).
Hence, the flag will flutter almost due east.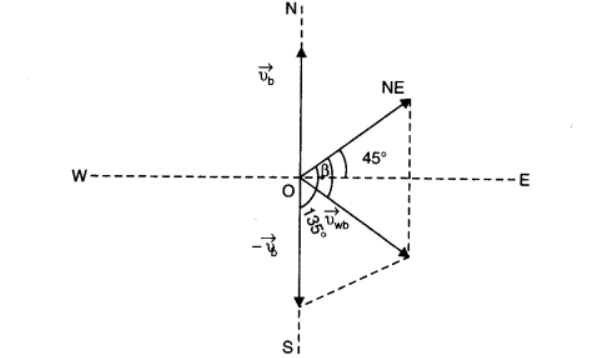
-
Question 25 of 50
25. Question
The ceiling of a long hall is \(25 \mathrm{~m}\) high. What is the maximum horizontal distance that a ball thrown with a speed of \(40 \mathrm{~m} \mathrm{~s}^{-1}\) can go without hitting the ceiling of the hall?
CorrectIncorrectHint
Height of the ceiling \(=25 \mathrm{~m}=\) Maximum height attained by the ball.
Velocity of the ball, \(\mathrm{u}=40 \mathrm{~m} / \mathrm{s}\)
Maximum height is given by \(\mathrm{h_{m}}=\frac{\mathrm{u}^{2} \sin ^{2} \theta}{2 g}\)
\(
\begin{aligned}
&\text { i.e., } \sin ^{2} \theta=\frac{2 \mathrm{gH}}{\mathrm{u}^{2}}=\frac{2 \times 9.8 \times 25}{(40)^{2}}=0.30625 \\
&\therefore \quad \sin \theta=\sqrt{0.30625}=0.5534 \\
&\Rightarrow \quad \theta=33.6
\end{aligned}
\)
\(\therefore\) Maximum horizontal distance,
\(
\begin{aligned}
R &=\frac{u^{2} \sin 2 \theta}{g}=\frac{(40)^{2} \sin 67.2}{9.8} \\
&=150.5 \mathrm{~m}
\end{aligned}
\) -
Question 26 of 50
26. Question
A cricketer can throw a ball to a maximum horizontal distance of \(100 \mathrm{~m}\). How much high above the ground can the cricketer throw the same ball?
CorrectIncorrectHint
Maximum horizontal distance, \(\mathrm{R_{m}}=100 \mathrm{~m}\)
The cricketer will only be able to throw the ball to the maximum horizontal distance when the angle of projection is \(45^{\circ}\), i.e. \(\theta=45^{\circ}\).The max horizontal range for a projection velocity \(v\) is given by the relation:
\(
\mathrm{R}_{m }=\frac{\mathrm{u}^{2}}{\mathrm{~g}}
\)
\(
100=\frac{\mathrm{u}^{2}}{\mathrm{~g}}
\)
The ball will achieve the maximum height when it is thrown vertically upward. For such motion, the final velocity \(v\) is zero at the maximum height \(\mathrm{h_{m}}\). Acceleration, \(\mathrm{a}=\mathrm{-g}\)
Using the third equation of motion:
\(
\mathrm{v}^{2}-\mathrm{u}^{2}=-2 \mathrm{gh_{m}}
\)
\(
\mathrm{h_{m}}=\mathrm{u}^{2} / 2 \mathrm{~g}=100 / 2=50 \mathrm{~m}
\) -
Question 27 of 50
27. Question
A stone tied to the end of a string \(80 \mathrm{~cm}\) long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in \(25 \mathrm{~s}\), what is the magnitude and direction of acceleration of the stone?
CorrectIncorrectHint
Here \(r=80 \mathrm{~cm}=0.8 \mathrm{~m}\);
\(
\begin{aligned}
&v=14 / 25 \mathrm{rev} / \mathrm{s} \\
&\omega=2 \pi v=2 \times \frac{22}{7} \times \frac{14}{25} \mathrm{rad} / \mathrm{s}=\frac{88}{25} \mathrm{rad} \mathrm{s}^{-1}
\end{aligned}
\)
The centripetal acceleration
\(
a=\omega^{2} r=\left(\frac{88}{25}\right)^{2} \times 0.80=9.90 \mathrm{~ms}^{-2}
\)
The direction of centripetal acceleration is along the string directed towards the centre of circular path. -
Question 28 of 50
28. Question
An aircraft executes a horizontal loop of radius \(1.00 \mathrm{~km}\) with a steady speed of 900 \(\mathrm{km} / \mathrm{h}\). Compare its centripetal acceleration with the acceleration due to gravity.
CorrectIncorrectHint
Radius of the loop, \(r=1 \mathrm{~km}=1000 \mathrm{~m}\)
Speed of the aircraft, \(v=900 \mathrm{~km} / \mathrm{h}=900 \mathrm{x} 5 / 18=250 \mathrm{~m} / \mathrm{s}\)
Centripetal acceleration, \(a_{c}=\frac{v^{2}}{r}\)
\(
=\frac{(250)^{2}}{1000}=62.5 \frac{m}{s^{2}}
\)
Acceleration due to gravity, \(\mathrm{g}=9.8 \mathrm{~m} / \mathrm{s}^{2}\)
\(
\begin{aligned}
\frac{a_{c}}{g} &=\frac{62.5}{9.8}=6.38 \\
a_{c} &=6.38 g
\end{aligned}
\) -
Question 29 of 50
29. Question
The position of a particle is given by
\(
\mathbf{r}=3.0 t \hat{\mathbf{i}}-2.0 t^{2} \hat{\mathbf{j}}+4.0 \hat{\mathbf{k}} \mathrm{m}
\)
where \(t\) is in seconds and the coefficients have the proper units for \(\mathbf{r}\) to be in metres.
(a) Find the \(\mathbf{v}\) and \(\mathbf{a}\) of the particle? (b) What is the magnitude and direction of velocity of the particle at \(t=2.0 \mathrm{~s}\)?CorrectIncorrectHint
(a) Here
\(
\vec{r}(t)=\left(3.0 t \hat{i}-2.0 t^{2} \hat{j}+4.0 \hat{k}\right) \mathrm{m}
\)
\(\therefore\)
\(
\vec{v}(t)=\frac{\overrightarrow{d r}}{d t}=(3.0 \hat{i}-4.0 t \hat{j}) \mathrm{m} / \mathrm{s}
\)
and
\(
\vec{a}(t)=\frac{\overrightarrow{d v}}{d t}=(-4.0 \hat{j}) \mathrm{m} / \mathrm{s}^{2}
\)(b) Magnitude of velocity at \(t=2.0 \mathrm{~s}\),
\(
\begin{aligned}
v_{(t=2 s)} &=\sqrt{(3.0)^{2}+(-4.0 \times 2)^{2}}=\sqrt{9+64}=\sqrt{73} \\
&=8.54 \mathrm{~m} \mathrm{~s}^{-1}
\end{aligned}
\)
This velocity will subtend an angle \(\beta\) from \(x\)-axis, where \(\tan \beta=\frac{(-4.0 \times 2)}{(3.0)}=-2.667\). \(=-2.6667 .\)
\(\therefore \quad \beta=\tan ^{-1}(-2.6667)=-69.44^{\circ}=69.44^{\circ}\) from negative \(x\)-axis. -
Question 30 of 50
30. Question
A particle starts from the origin at \(t=0 \mathrm{~s}\) with a velocity of \(10.0 \hat{\mathrm{j}} \mathrm{m} / \mathrm{s}\) and moves in the \(x-y\) plane with a constant acceleration of \((8.0 \hat{\mathbf{i}}+2.0 \hat{\mathbf{j}}) \mathrm{m} \mathrm{s}^{-2}\). (a) At what time is the \(x\)-coordinate of the particle \(16 \mathrm{~m}\)? What is the \(y\)-coordinate of the particle at that time? (b) What is the speed of the particle at the time?
CorrectIncorrectHint
The initial velocity of particle is \(\overrightarrow{\mathrm{u}}=10 \mathrm{jm} / \mathrm{s}\)
The acceleration of the particle is \(\vec{a}=8 \hat{i}+2 \hat{j}\)
(a) The position of the particle at any instant is given by:
\(
\overrightarrow{\mathrm{s}}=\overrightarrow{\mathrm{u} t}+\frac{1}{2} \overrightarrow{\mathrm{a}} \mathrm{t}^{2}
\)
\(
x \hat{i}+y \hat{j}=4 t^{2} \hat{i}+\left(10 t+t^{2}\right) \hat{j}
\)
Comparing the \(\mathrm{x}\) and \(\mathrm{y}\) component of the position:
\(x=4 t^{2}\)
\(
x=16 \Rightarrow t=2 s
\)
\(
y=10 t+t^{2}
\)
At \(\mathrm{t}=2, \mathrm{y}=24 \mathrm{~m}\)(b) The speed of the particle at any instant is given by:
\(
\begin{aligned}
&\vec{v}=\vec{u}+\vec{a} t \\
&\vec{v}=10 \hat{j}+(8 \hat{i}+2 \hat{j}) 2
\end{aligned}
\)
\( \vec{v}=14 \hat{j}+16 \hat{i}\)
\(
|\vec{v}|=\sqrt{14^{2}+16^{2}}=21.26 \mathrm{~m} / \mathrm{s}
\) -
Question 31 of 50
31. Question
An aircraft is flying at a height of \(3400 \mathrm{~m}\) above the ground. If the angle subtended at a ground observation point by the aircraft positions \(10.0 \mathrm{~s}\) apart is \(30^{\circ}\), what is the speed of the aircraft?
CorrectIncorrectHint
In the Figure below “O” is the observation point at the ground. A and B are the positions of aircraft for which \(\angle \mathrm{AOB}=30^{\circ}\). Draw a perpendicular \(O C\) on \(A B\). Here \(O C=3400 \mathrm{~m}\) and \(\angle A O C\) \(=\angle \mathrm{COB}=15^{\circ}\).
In \(\triangle \mathrm{AOC}, A C=O C \tan 15^{\circ}=3400 \times 0.2679=910.86 \mathrm{~m}\). \(A B=A C+C B=A C+A C=2 A C=2 \times 910.86 \mathrm{~m}\)
Speed of the aircraft, \(v=\frac{\text { distance } A B}{\text { time }}=\frac{2 \times 910.86}{10}= 182.17 \mathrm{~ms}^{-1}=182.2 \mathrm{~ms}^{-1}\)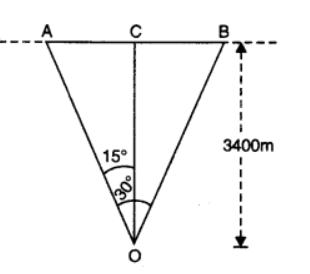
-
Question 32 of 50
32. Question
A bullet fired at an angle of \(30^{\circ}\) with the horizontal hits the ground \(3.0 \mathrm{~km}\) away. By adjusting its angle of projection, can one hope to hit a target \(5.0 \mathrm{~km}\) away? Assume the muzzle speed to be fixed, and neglect air resistance.
CorrectIncorrectHint
Here \(R=3 \mathrm{~km}=3000 \mathrm{~m}, \theta=30^{\circ}, g=9.8 \mathrm{~m} \mathrm{~s}^{-2}\).
As \(R=\frac{u^{2} \sin 2 \theta}{g}\)
\(\begin{aligned} \Rightarrow & 3000 =\frac{u^{2} \sin 2 \times 30^{\circ}}{9.8}=\frac{u^{2} \sin 60}{9.8} \\ \Rightarrow & u^{2} =\frac{3000 \times 9.8}{\sqrt{3} / 2}=3464 \times 9.8 \\ \text { Also, } & R^{\prime} =\frac{u^{2} \sin 2 \theta^{\prime}}{g} \Rightarrow 5000=\frac{3464 \times 9.8 \times \sin 2 \theta}{9.8} \end{aligned}\)
\(
\text { i.e., } \quad \sin 2 \theta^{\prime}=\frac{5000}{3464}=1.44
\)
which is impossible because sine of an angle cannot be more than 1 . Thus this target cannot be hoped to be hit. -
Question 33 of 50
33. Question
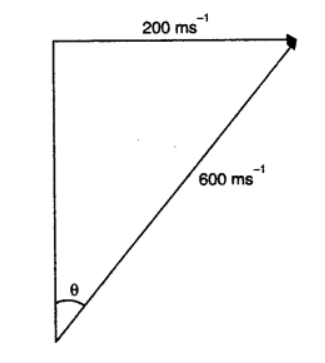
A fighter plane flying horizontally at an altitude of \(1.5 \mathrm{~km}\) with speed \(720 \mathrm{~km} / \mathrm{h}\) passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed \(600 \mathrm{~m} \mathrm{~s}^{-1}\) to hit the plane? At what minimum altitude should the pilot fly the plane to avoid being hit? (Take \(g=10 \mathrm{~m} \mathrm{~s}^{-2}\) ).
CorrectIncorrectHint
Velocity of plane, \(v_{p}=720 \times 5 / 180 \mathrm{~ms}^{-1}=200 \mathrm{~ms}^{-1}\)
Velocity of shell \(=600 \mathrm{~ms}^{-1}\);
\(
\begin{aligned}
\sin \theta &=\frac{200}{600}=\frac{1}{3} \\
\theta &=\sin ^{-1}\left(\frac{1}{3}\right)=19.47^{\circ}
\end{aligned}
\)
This angle is with the vertical. Let \(h_{min}\) be the required minimum height.
Using equation
\(
\begin{aligned}
v^{2}-u^{2} =2 \text { as, we get } \\
(0)^{2}-(600 \cos \theta)^{2} =-2 \times 10 \times h_{min} \\
h_{min} \quad =\frac{600 \times 600\left(1-\sin ^{2} \theta\right)}{20} \\
=30 \times 600\left(1-\frac{1}{9}\right)=\frac{8}{9} \times 30 \times 600 \mathrm{~m}=16 \mathrm{~km} .
\end{aligned}
\)
-
Question 34 of 50
34. Question
A cyclist is riding with a speed of \(27 \mathrm{~km} / \mathrm{h}\). As he approaches a circular turn on the road of radius \(80 \mathrm{~m}\), he applies brakes and reduces his speed at the constant rate of \(0.50 \mathrm{~m} / \mathrm{s}\) every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?
CorrectIncorrectHint
Here \(v=27 \mathrm{~km} / \mathrm{h}=27 \times \frac{5}{18} \mathrm{~m} / \mathrm{s}=7.5 \mathrm{~m} / \mathrm{s}, r=80 \mathrm{~m}\) and tangential acceleration \(a_{t}=-0.50 \mathrm{~m} / \mathrm{s}^{2}\)
\(\therefore\) Centripetal acceleration \(a_{c}=\frac{v^{2}}{r}=\frac{(7.5)^{2}}{80}=0.70 \mathrm{~ms}^{-2}\) (radially inwards).
Thus, as shown in fig. above, two accelerations are acting in mutually perpendicular directions. If \(\vec{a}\) be the resultant acceleration, then
\(
|\vec{a}|=\sqrt{a_{t}^{2}+a_{c}^{2}}=\sqrt{(0.5)^{2}+(0.7)^{2}}=0.86 \mathrm{~ms}^{-2}
\)and \(\quad \tan \beta=\frac{a_{c}}{a_{t}}=\frac{0.7}{0.5}=1.4\)
\(\Rightarrow \quad \beta=\tan ^{-1}(1.4)=54.5^{\circ}\) from the direction of negative of the velocity.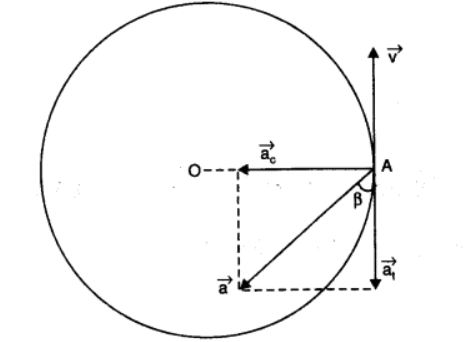
-
Question 35 of 50
35. Question
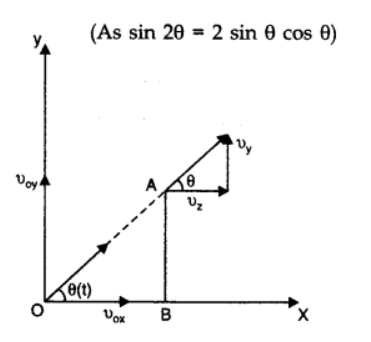
(a) A projectile the angle between the velocity and the \(x\)-axis as a function of time is given by \(\theta(t)=\tan ^{-1}\left(\frac{v_{0 y}-g t}{v_{o x}}\right)\). Is this true?
(b) The projection angle \(\theta_{0}\) for a projectile launched from the origin is given by
\(\theta_{0}=\tan ^{-1}\left(\frac{4 h_{m}}{R}\right)\). where the symbols have their usual meaning. Is this statement true?CorrectIncorrectHint
(a) Let the projectile be fired at an angle \(\theta\) with \(x\)-axis.
As \(\theta\) depends on \(t, \theta(t)\), at any instant
\(
\begin{aligned}
\tan \theta(t)=\frac{v_{y}}{v_{x}}=\frac{v_{o y}-g t}{v_{o x}} \\ \quad\left(\text { Since } v_{y}=v_{o y}-g t \text { and } v_{x}=v_{o x}\right) \\
\theta(t) =\tan ^{-1}\left(\frac{v_{o y}-g t}{v_{o x}}\right)
\end{aligned}
\)Since,
\(
h_{\max }=\frac{u^{2} \sin ^{2} \theta}{2 g}
\)\(\begin{aligned} & \text { and } R =\frac{u^{2} \sin 2 \theta}{g} \\ \Rightarrow & \frac{h_{\max }}{R} =\frac{u^{2} \sin ^{2} \theta / 2 g}{u^{2} \sin 2 \theta / g}=\frac{\tan \theta}{4} \\ \Rightarrow & \frac{\tan \theta}{4} =\frac{h_{\max }}{R} \\ & \text { or } \tan \theta =\frac{4 h_{\max }}{R} \\ & \text { or } \theta =\tan ^{-1}\left(\frac{4 h_{\max }}{R}\right) . \end{aligned}\)
-
Question 36 of 50
36. Question
Let \(\vec{a}=4 \vec{i}+3 \vec{j}\) and \(\vec{b}=3 \vec{i}+4 \vec{j}\). (a) Find the magnitudes of (a) \(\vec{a}\), (b) \(\vec{b}\), (c) \(\vec{a}+\vec{b}\) and (d) \(\vec{a}-\vec{b}\).
CorrectIncorrectHint
\(
\vec{a}=4 \vec{i}+3 \vec{j}, \vec{b}=3 \vec{i}+4 \vec{j}
\)
a) \(|\vec{a}|=\sqrt{4^2+3^2}=5\)
b) \(|\vec{b}|=\sqrt{9+16}=5\)
c) \(|\vec{a}+\overrightarrow{\mathrm{b}}|=|7 \overrightarrow{\mathrm{i}}+7 \overrightarrow{\mathrm{j}}|=7 \sqrt{2}\)
d)
\(
\begin{aligned}
& \vec{a}-\vec{b}=(-3+4) \hat{i}+(-4+3) \hat{j}=\hat{i}-\hat{j} \\
& |\vec{a}-\vec{b}|=\sqrt{1^2+(-1)^2}=\sqrt{2}
\end{aligned}
\) -
Question 37 of 50
37. Question
A spy report about a suspected car reads as follows. “The car moved \(2.00 \mathrm{~km}\) towards east, made a perpendicular left turn, ran for \(500 \mathrm{~m}\), made a perpendicular right turn, ran for \(4.00 \mathrm{~km}\) and stopped”. Find the displacement of the car.
CorrectIncorrectHint
The displacement of the car is represented by \(\overrightarrow{A D}\).
\(
\begin{aligned}
& \overrightarrow{A D}=2 \hat{i}+0.5 \hat{j}+4 \hat{i} \\
& =6 \hat{i}+0.5 \hat{j}
\end{aligned}
\)
Magnitude of \(\overrightarrow{A D}\) is given by
\(
\begin{aligned}
& A D=\sqrt{A E^2+D E^2} \\
& =\sqrt{6^2+(0.5)^2} \\
& =\sqrt{36+0.25}=6.02 \mathrm{~km}
\end{aligned}
\)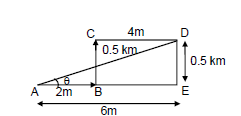
Now,
\(
\begin{aligned}
& \tan \theta=\frac{D E}{A E}=\frac{1}{12} \\
& \Rightarrow \theta=\tan ^{-1}\left(\frac{1}{12}\right)
\end{aligned}
\)
Hence, the displacement of the car is \(6.02 \mathrm{~km}\) along the direction \(\tan ^{-1}\left(\frac{1}{12}\right)\) with positive the \(x\)-axis. -
Question 38 of 50
38. Question
Suppose \(\vec{a}\) is a vector of magnitude 4.5 unit due north. What is the vector (a) \(3 \vec{a}\), (b) \(-4 \vec{a}\)?
CorrectIncorrectHint
\(\vec{a}\) is a vector of magnitude 4.5 unit due north.
a) \(3|\vec{a}|=3 \times 4.5=13.5\)
\(3 \vec{a}\) is along north having magnitude 13.5 units.
b) \(-4|\vec{a}|=-4 \times 4.5=-18\) unit
\(-4 \vec{a}\) is a vector of magnitude 18 unit due south. -
Question 39 of 50
39. Question
Let \(\vec{a}=2 \vec{i}+3 \vec{j}+4 \vec{k}\) and \(\vec{b}=3 \vec{i}+4 \vec{j}+5 \vec{k}\). Find the angle between them.
CorrectIncorrectHint
We have:
\(
\begin{aligned}
& \vec{a}=2 \vec{i}+3 \vec{j}+4 \vec{k} \\
& \vec{b}=3 \vec{i}+4 \vec{j}+5 \vec{k}
\end{aligned}
\)
Using scalar product, we can find the angle between vectors \(\vec{a}\) and \(\vec{b}\). i.e.,
\(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta\)
So, \(\theta=\cos ^{-1}\left(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\right)\)
\(=\cos ^{-1}\left(\frac{2 \times 3+3 \times 4+4 \times 5}{\sqrt{\left(2^2+3^2+4^2\right)} \sqrt{\left(3^2+4^2+5^2\right)}}\right)\)
\(=\cos ^{-1}\left(\frac{38}{\sqrt{29} \sqrt{50}}=\cos ^{-1} \frac{38}{\sqrt{1450}}\right)\)
\(\therefore\) The required angle is \(\cos ^{-1} \frac{38}{\sqrt{1450}}\). -
Question 40 of 50
40. Question
\(
\text { If } \vec{A}=2 \vec{i}+3 \vec{j}+4 \vec{k} \text { and } \vec{B}=4 \vec{i}+3 \vec{j}+2 \vec{k} \text {, find } \vec{A} \times \vec{B}
\)CorrectIncorrectHint
Given:
\(
\begin{aligned}
& \vec{A}=2 \hat{i}+3 \hat{j}+4 \hat{k} \text { and } \\
& \vec{B}=4 \hat{i}+3 \hat{j}+2 \hat{k}
\end{aligned}
\)
The vector product of \(\vec{A} \times \vec{B}\) can be obtained as follows:
\(
\begin{aligned}
& \vec{A} \times \vec{B}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
2 & 3 & 4 \\
4 & 3 & 2
\end{array}\right| \\
& =\hat{i}(6-12)-\hat{j}(4-16)+\hat{k}(6-12) \\
& =-6 \hat{i}+12 \hat{j}-6 \hat{k}
\end{aligned}
\) -
Question 41 of 50
41. Question
Find the area bounded under the curve \(y=3 x^2+6 x+7\) and the \(X\)-axis with the ordinates at \(x=5\) and \(x=10\).
CorrectIncorrectHint
\(
y=3 x^2+6 x+7
\)
\(\therefore\) Area bounded by the curve, \(x\) axis with coordinates with \(x=5\) and \(x=10\) is given by,
\(
\text { Area } \left.\left.\left.=\int_0^y d y=\int_5^{10}\left(3 x^2+6 x+7\right) d x=3 \frac{x^3}{3}\right]_5^{10}+5 \frac{x^2}{3}\right]_5^{10}+7 x\right]_5^{10}=1135 \text { sq.units. }
\)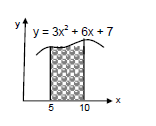
-
Question 42 of 50
42. Question
Find the area enclosed by the curve \(y=\sin x\) and the \(X\)-axis between \(x=0\) and \(x=\pi\).
CorrectIncorrectHint
\(
\text { Area }=\int_0^y d y=\int_0^\pi \sin x d x=-[\cos x]_0^\pi=2
\)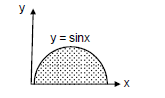
-
Question 43 of 50
43. Question
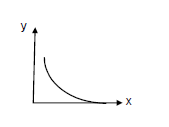
Find the area bounded by the curve \(y=e^{-x}\), the \(X\)-axis and the \(Y\)-axis.
CorrectIncorrectHint
The given function is \(y=e^{-x}\).
When \(x=0, y=e^{-0}=1\)
When \(x\) increases, the value of \(y\) decrease. Also, only when \(x=\infty, y=0\)
So, the required area can be determined by integrating the function from 0 to \(\infty\).
\(
\begin{aligned}
& \therefore \text { Area }=\int_0^{\infty} e^{-x} d x \\
& =-\left[e^{-x}\right]_0^{\infty} \\
& =-[0-1]=1 \mathrm{~sq} \cdot \mathrm{unit}
\end{aligned}
\)
-
Question 44 of 50
44. Question
The momentum \(p\) of a particle changes with time \(t\) according to the relation \(\frac{d p}{d t}=(10 \mathrm{~N})+(2 \mathrm{~N} / \mathrm{s}) t\). If the momentum is zero at \(t=0\), what will the momentum be at \(t=10 \mathrm{~s}\)?
CorrectIncorrectHint
According to the question, we have:
\(
\frac{d p}{d t}=(10 N)+(2 N / s) t
\)
Momentum is zero at time, \(\mathrm{t}=0\)
Now, \(d p=\left[(10 \mathrm{~N})+\left(2 \mathrm{Ns}^{-1}\right) t\right] d t\)
On integrating the above equation, we get:
\(
\begin{aligned}
& p=\int_0^{10} d p=\int_0^{10} 10 d t+\int_0^{10}(2 t d t) \\
& \Rightarrow p=\left[10 t+2 \frac{t^2}{2}\right]_0^{10} \\
& \Rightarrow p=10 \times 10+100-0 \\
& \therefore p=100+100=200 \mathrm{~kg} \mathrm{~m} / \mathrm{s}
\end{aligned}
\) -
Question 45 of 50
45. Question
The changes in a function \(y\) and the independent variable \(x\) are related as \(\frac{d y}{d x}=x^2\). Find \(y\) as a function of \(x\).
CorrectIncorrectHint
Changes in a function of \(y\) and the independent variable \(x\) are related as follows:
\(
\begin{aligned}
& \frac{d y}{d x}=x^2 \\
& \Rightarrow d y=x^2 d x
\end{aligned}
\)
Integrating of both sides, we get:
\(
\begin{aligned}
& \int d y=\int x^2 d x \\
& \Rightarrow y=\frac{x^3}{3}+c
\end{aligned}
\)
where \(c\) is a constant
\(\therefore y\) as a function of \(x\) is represented by
\(
y=\frac{x^3}{3}+c
\) -
Question 46 of 50
46. Question
Write the number of significant digits in (a) 1001, (b) \(100 \cdot 1\), (c) \(100 \cdot 10\), (d) \(0 \cdot 001001\).
CorrectIncorrectHint
(a) 1001
Number of significant digits =4
(b) 100.1
Number of significant digits =4
(c) 100.10
Number of significant digits =5
(d) 0.001001
Number of significant digits =4 -
Question 47 of 50
47. Question
A metre scale is graduated at every millimetre. How many significant digits will be there in a length measurement with this scale?
CorrectIncorrectHint
The metre scale is graduated at every millimetre.
i.e., \(1 \mathrm{~m}=1000 \mathrm{~mm}\)
The minimum number of significant digits may be one (e.g., for measurements like \(4 \mathrm{~mm}\) and \(6 \mathrm{~mm}\) ) and the maximum number of significant digits may be 4 (e.g., for measurements like \(1000 \mathrm{~mm}\) ). Hence, the number of significant digits may be \(1,2,3\) or 4 . -
Question 48 of 50
48. Question
The length and the radius of a cylinder measured with a slide callipers are found to be \(4.54 \mathrm{~cm}\) and \(1.75 \mathrm{~cm}\) respectively. Calculate the volume of the cylinder.
CorrectIncorrectHint
Length of the cylinder, \(l=4.54 \mathrm{~cm}\)
Radius of the cylinder, \(r=1.75 \mathrm{~cm}\)
Volume of the cylinder, \(V=\pi r^2 l=(\pi) \times(4.54) \times(1.75)^2\)The minimum number of significant digits in a particular term is three. Therefore, the result should have three significant digits, while the other digits should be rounded off.
\(
\begin{aligned}
& \therefore \text { Volume, } V=\pi r^2 l \\
& =(3.14) \times(1.75) \times(1.75) \times(4.54) \\
& =43.6577 \mathrm{~cm}^3
\end{aligned}
\)
Since the volume is to be rounded off to 3 significant digits, we have:
\(
V=43.7 \mathrm{~cm}^3
\)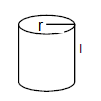
-
Question 49 of 50
49. Question
The thickness of a glass plate is measured to be \(2.17 \mathrm{~mm}, 2 \cdot 17 \mathrm{~mm}\) and \(2.18 \mathrm{~mm}\) at three different places. Find the average thickness of the plate from this data.
CorrectIncorrectHint
We know that,
Average thickness \(=\frac{2.17+2.17+2.18}{3}=2.1733 \mathrm{~mm}\)
Rounding off to 3 significant digits, average thickness \(=2.17 \mathrm{~mm}\). -
Question 50 of 50
50. Question
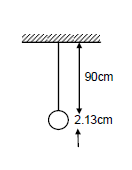
The length of the string of a simple pendulum is measured with a metre scale to be \(90.0 \mathrm{~cm}\). The radius of the bob plus the length of the hook is calculated to be \(2 \cdot 13 \mathrm{~cm}\) using measurements with a slide callipers. What is the effective length of the pendulum? (The effective length is defined as the distance between the point of suspension and the centre of the bob.)
CorrectIncorrectHint
As shown in the figure,
Actual effective length \(=(90.0+2.13) \mathrm{cm}\)
But, in the measurement \(90.0 \mathrm{~cm}\), the no. of significant digits is only 2 .
So, the addition must be done by considering only 2 significant digits of each measurement.
So, effective length \(=90.0+2.1=92.1 \mathrm{~cm}\).