Past NEET Entrance Papers
Quiz Summary
0 of 83 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 83 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 83
1. Question
\(
{ }_{82}^{290} X \xrightarrow{\alpha} Y \xrightarrow{e^{+}} Z \xrightarrow{\beta^{-}} P \xrightarrow{e^{-}} Q
\)
In the nuclear emission stated above, the mass number and atomic number of the product \(Q\) respectively, are: [NEET 2024]CorrectIncorrectHint
(c) Step 1: Effect of Alpha ( \(\alpha\) ) Decay
An alpha particle \((\alpha)\) has a mass number of 4 and an atomic number of 2 .
When element \(X\) undergoes alpha decay:
\(
{ }_{82}^{290} X \xrightarrow_{80}^{286} Y+{ }_2^4 \alpha
\)
Thus, the new nucleus \(Y\) has:
Mass number \(=290-4=286\)
Atomic number \(=82-2=80\)
Step 2: Effect of Positron \(\left(e^{+}\right)\)Emission
Positron emission ( \(\beta^{+}\)) decreases the atomic number by 1 without changing the mass number:
\(
{ }_{80}^{286} Y \xrightarrow_{79}^{286} Z+e^{+}
\)
Thus, \(Z\) has:
Mass number \(=286\) (unchanged)
Atomic number \(=80-1=79\)
Step 3: Effect of Beta-Minus ( \(\beta^{-}\)) Decay
Beta-minus ( \(\beta^{-}\)) emission increases the atomic number by 1 without affecting the mass number:
\(
{ }_{79}^{286} Z\xrightarro_{80}^{286} P+\beta^{-}
\)
Thus, \(P\) has:
Mass number \(=286\) (unchanged)
Atomic number \(=79+1=80\)
Step 4: Effect of Electron Capture ( \(e^{-}\))
Electron capture decreases the atomic number by 1, keeping the mass number unchanged:
\(
{ }_{80}^{286} P+e^{-}\xrightarrow_{81}^{286} Q
\)
Thus, \(Q\) has:
Mass number \(=286\) (unchanged)
Atomic number \(=80+1=81\)
The final product \(Q\) has mass number 286 and atomic number 81. -
Question 2 of 83
2. Question
The ratio of nuclear densities and nuclear volumes of \({ }_{26}^{56} \mathrm{Fe}\) and \({ }_2^4 \mathrm{He}\) are, respectively: [NEET 2024]
CorrectIncorrectHint
(c) \(1: 1[latex] and [latex]14: 1\).
Explanation:
Nuclear Density:
Nuclear density is roughly constant for all nuclei, meaning it’s independent of the mass number. Therefore, the ratio of densities between two nuclei is always 1:1.Nuclear Volume:
The volume of a nucleus is proportional to the cube of its radius, and the radius is proportional to the cube root of the mass number (A). Therefore, if the ratio of mass numbers \(A 1 / A 2=56 / 4=14\), then the ratio of the nuclear volumes is \(14: 1\). -
Question 3 of 83
3. Question
An excited heavy nucleus \({ }_Z^A \mathrm{X}\) emits radiations in the following sequence:
\(
{ }_Z^A \mathrm{X} \rightarrow{ }_{Z-2}^{A-4} \mathrm{D}_1 \rightarrow{ }_{Z-1}^{A-4} \mathrm{D}_2 \rightarrow_{Z-3}^{A-8} \mathrm{D}_3 \rightarrow_{Z-4}^{A-8} \mathrm{D}_4 \rightarrow_{Z-4}^{A-8} \mathrm{D}_5
\)
where \(Z, A\) are the atomic and mass number of element \(X\) , respectively. The possible emitted particles or radiations in the sequence, respectively are: [NEET 2024]CorrectIncorrectHint
(c) Alpha particle emission reduces the atomic number by 2 and the mass number by 4.
Beta minus ( \(e^{-}\)) emission increases the atomic number by 1 and does not change the mass number.
Beta plus ( \(e^{+}\)) emission decreases the atomic number by 1 and does not change the mass number.
Gamma radiation emission does not change the atomic number or the mass number.
Step 1: Identify the first emitted particle
The atomic number decreases by 2 and the mass number decreases by 4 . This corresponds to the emission of an alpha particle ( \(\alpha\) ).Step 2: The atomic number increases by 1 and the mass number remains the same. This corresponds to the emission of a beta minus particle ( \(e^{-}\)).
Step 3: The atomic number decreases by 2 and the mass number decreases by 4 . This corresponds to the emission of an alpha particle ( \(\alpha\) ).
Step 4: The atomic number decreases by 1 and the mass number remains the same. This corresponds to the emission of a beta plus particle \(\left(e^{+}\right)\).
Step 5: The atomic number and mass number remain the same.
This corresponds to the emission of gamma radiation ( \(\gamma\) ).The sequence of emitted particles or radiations is \(\alpha, e^{-}, \alpha, e^{+}, \gamma\).
-
Question 4 of 83
4. Question
Water is used as a coolant in a nuclear reactor because of its: [NEET 2024]
CorrectIncorrectHint
(b) High specific heat capacity
Explanation:
Water is used as a coolant in nuclear reactors primarily due to its high specific heat capacity. This property allows water to absorb a significant amount of heat without a large increase in temperature. making it effective in regulating the reactor’s temperature and preventing overheating. -
Question 5 of 83
5. Question
\(
\begin{aligned}
&\text { Select the correct statements among the following: }\\
&\begin{array}{|l|l|}
\hline \text { A. } & \text { slow neutrons can cause fission in } \mathrm{U}_{92}^{235} \text { than fast neutrons. } \\
\hline \text { B. } & \alpha \text {-rays are helium nuclei. } \\
\hline \text { C. } & \beta \text {-rays are fast-moving electrons or positrons. } \\
\hline \text { D. } & \gamma \text {-rays are electromagnetic radiations of wavelengths larger than } X \text {-rays. } \\
\hline
\end{array}
\end{aligned}
\)
Choose the most appropriate answer from the options given below: [NEET 2024]CorrectIncorrectHint
(a) (A) Slow neutron can cause fission in \({ }_{92}^{235} \mathrm{U}\) than fast neutrons because fast neutrons are too quick so they scatter of atoms instead of being captured by them
(B) \(\alpha\)-rays are Helium nuclei, is a true statement
(C) \(\beta\)-rays are generated when neutron is converted into proton by releasing electron or proton is converted into neutron by releasing positron.
(D) \(\gamma\)-rays have higher energies as compared to \(X\)-rays. So they have smaller wavelength as compared to X-rays. -
Question 6 of 83
6. Question
In the given nuclear reaction, the element X is:
\({ }_{11}^{22} \mathrm{Na} \rightarrow \mathrm{X}+\mathrm{e}^{+}+\nu\) [NEET 2022]CorrectIncorrectHint
(d) To solve the nuclear reaction given as \(\mathrm{Na}_{11}^{22} \rightarrow X+e^{+}+\nu\), we need to determine the element \(X\).
Identify the Initial Element:
The initial element is Sodium ( Na ) with atomic number 11 and mass number 22, represented as \({ }_{11}^{22} \mathrm{Ne}\)[/latex].
2. Understand the Reaction:
The reaction indicates that Sodium is undergoing a beta-plus decay ( \(\beta+\) decay), where a positron ( \(e^{+}\)) and a neutrino ( \(\nu\) ) are emitted.
3. Apply the Conservation Laws:
Mass Number Conservation: The mass number before the reaction must equal the mass number after the reaction. Since the positron and neutrino have negligible mass, the mass number of \(X\) must remain 22 .
Atomic Number Conservation: The atomic number decreases by 1 due to the emission of the positron. Therefore, the atomic number of \(X\) will be \(11-1=10\).
4. Determine the Element:
The element with atomic number 10 is \(\mathrm{Neon}(\mathrm{Ne})\). Therefore, we can write:
\(
X=\mathrm{Ne}_{10}^{22}
\)
5. Final Answer: The final answer for the element \(X\) is \({ }_{10}^{22} \mathrm{Ne}\).
\({ }_{10}^{22} \mathrm{Ne}\) -
Question 7 of 83
7. Question
A nucleus of mass number 189 splits into two nuclei having mass numbers 125 and 64 . The ratio of the radius of two daughter nuclei respectively is: [NEET 2022]
CorrectIncorrectHint
(d) The distance from the center to the point where the density has reduced to half its initial value is known as the nuclear radius, or \(R\). These radii can be measured experimentally by fast neutron deflection tests.
For this nuclear radii are given as \(R=R_0 A^{1 / 3}\)
where \(R=\) nuclear radii, \(A=\) atomic mass number, \(R_0=1.3 \mathrm{FM}\) which is constant for every nuclei.
Calculation:
Given:
Atomic mass number of nuclei \(1\left(\mathrm{~A}_1\right)=125\)
atomic mass number of nuclei \(2\left(\mathrm{~A}_2\right)=64\)
the ratio of the radius of two nuclei is \(=\frac{R(125)}{R(64)}=\frac{R_0 A_1^{1 / 3}}{R_0 A_2^{1 / 3}}\)
\(
\Rightarrow \frac{R(125)}{R(64)}=(125 / 64)^{1 / 3}=5 / 4
\) -
Question 8 of 83
8. Question
A nucleus with mass number 240 breaks into fragments each of mass number 120. The binding energy per nucleon of unfragmented nuclei is 7.6 MeV while that of fragments is 8.5 MeV. The total gain in the binding energy in the process is: [NEET 2021]
CorrectIncorrectHint
(b) Mass number of the original nucleus: 240
Mass number of each fragment: 120
Binding energy per nucleon of the original nucleus: 7.6 MeV
Binding energy per nucleon of each fragment: 8.5 MeV
The initial total binding energy is the product of the mass number and the binding energy per nucleon of the original nucleus.
\(
E_{\text {initial }}=240 \times 7.6 \mathrm{MeV}=1824 \mathrm{MeV}
\)
Since the nucleus breaks into two fragments, each with a mass number of 120 , the final total binding energy is the sum of the binding energies of the two fragments.
\(
E_{\text {final }}=2 \times(120 \times 8.5 \mathrm{MeV})=2 \times 1020 \mathrm{MeV}=2040 \mathrm{MeV}
\)
The gain in binding energy is the difference between the final and initial total binding energies.
\(
\Delta E=E_{\text {final }}-E_{\text {initial }}=2040 \mathrm{MeV}-1824 \mathrm{MeV}=216 \mathrm{MeV}
\)
The total gain in binding energy is 216 MeV. -
Question 9 of 83
9. Question
A radioactive nucleus \({ }_{\mathrm{Z}}^{\mathrm{A}} \mathrm{X}\) undergoes spontaneous decay in the sequence \({ }_{\mathrm{Z}}^{\mathrm{A}}{X} \rightarrow \mathrm{~B}_{\mathrm{Z}-1} \rightarrow \mathrm{C}_{\mathrm{Z}-3} \rightarrow \mathrm{D}_{\mathrm{Z}-2}\) where Z is the atomic number of element X. The possible decay particles in the sequence are: [NEET 2021]
CorrectIncorrectHint
(a)
\(
{ }_Z^A X \xrightarrow{\beta^{+}} Z_{-1} B \xrightarrow{\alpha} Z_{-3} C \xrightarrow{\beta^{-}} Z_{-2} D
\)
\(\beta^{+}\)decreases atomic number by 1
\(\alpha\) decreases atomic number by 2
\(\beta^{-}\)increases atomic number by 1. -
Question 10 of 83
10. Question
The energy equivalent of 0.5 g of a substance is: [NEET 2020]
CorrectIncorrectHint
(a)
\(
\begin{aligned}
&\text { From mass-energy equivalence, }\\
&\begin{aligned}
& E=m c^2 \\
& =0.5 \times 10^{-3} \times 9 \times 10^{16} \\
& =4.5 \times 10^{13} \mathrm{~J}
\end{aligned}
\end{aligned}
\) -
Question 11 of 83
11. Question
When a uranium isotope \({ }_{92}^{235} \mathrm{U}\) is bombarded with a neutron, it generates \({ }_{36}^{89} \mathrm{Kr}\), three neutrons and: [NEET 2020]
CorrectIncorrectHint
(d) Suppose after bombarding neutron we get \(X_Z^A\) along with \({ }_{36}^{89} \mathrm{Kr}\) and 3 neutrons. The reaction equation looks like;
\(
U_{92}^{235}+{ }_0^1 n \rightarrow K r_{36}^{89}+3 n_0^1+X_Z^A
\)
where \(\mathrm{A}=\) Atomic mass number and, Z is the Atomic number.
Now, \(\Sigma\) Atomic No in left-hand side \(=92+0=92\)
\(\mathbf{\Sigma A t o m i c}\) No in right-hand side \(=36+3 \times 0+Z=36+Z\)
\(\because\) Atomic No must be conserved.
\(\therefore \Sigma\) Atomic No on the left-hand side \(=\Sigma\) Atomic No on the right-hand side
\(
\begin{aligned}
& \Rightarrow 36+Z=92 \\
& \Rightarrow Z=56
\end{aligned}
\)
Also from the conservation of Mass-Number we have;
\(\Sigma\) Atomic Mass No on the left-hand side =\(\Sigma\) Atomic Mass No on the right-hand side
\(
\begin{aligned}
&\begin{aligned}
& \Rightarrow 235+1=89+3+A \\
& \Rightarrow A=144
\end{aligned}\\
&\text { So, }{ }_{56}^{144} X \text { is generated where } \mathrm{X}=\mathrm{Ba} \text {. }
\end{aligned}
\) -
Question 12 of 83
12. Question
What happens to the mass number and the atomic number of an element when it emits \(\gamma\)-radiation? [NEET 2020]
CorrectIncorrectHint
(b) When an element emits gamma radiation, neither its mass number nor its atomic number changes. Gamma rays are electromagnetic waves with no mass or charge, and their emission only involves the nucleus shifting from a higher en ergy state to a lower one, without altering the number of pro tons or neutrons.
-
Question 13 of 83
13. Question
\(\alpha\)-particle consists of : [NEET 2019]
CorrectIncorrectHint
(d) Since, \(\alpha\)-particle is equivalent to He -atom nucleus, hence it has two protons and two neutrons only.
-
Question 14 of 83
14. Question
If the radius of \({ }_{13}^{27} \mathrm{Al}\) nucleus is taken to be \(R_{\mathrm{Al}}\), then the radius of \({ }_{53}^{125} \mathrm{Te}\) nucleus is near: [NEET 2015]
CorrectIncorrectHint
(c) As we know, \(\mathrm{R}=\mathrm{R}_0(\mathrm{~A})^{1 / 3}\) where \(\mathrm{A}=\) mass number
\(
\begin{aligned}
& \mathrm{R}_{\mathrm{Al}}=\mathrm{R}_0(27)^{1 / 3}=3 \mathrm{R}_0 \\
& \mathrm{R}_{\mathrm{Te}}=\mathrm{R}_0(125)^{1 / 3}=5 \mathrm{R}_0=\frac{5}{3} \mathrm{R}_{\mathrm{Al}}
\end{aligned}
\) -
Question 15 of 83
15. Question
The Binding energy per nucleon of \({ }_3^7 \mathrm{Li}\) and \({ }_2^4 \mathrm{He}\) nucleon are 5.60 MeV and 7.06 MeV , respectively. In the nuclear reaction \({ }_3^7 \mathrm{Li}+{ }_1^1 \mathrm{H} \rightarrow{ }_2^4 \mathrm{He}+{ }_2^4 \mathrm{He}+Q\), the value of energy \(Q\) released is: [AIPMT 2014]
CorrectIncorrectHint
(d) The binding energy per nucleon of \({ }_3^7 \mathrm{Li}\) is 5.60 MeV.
The binding energy per nucleon of \({ }_2^4 \mathrm{He}\) is 7.06 MeV.
The number of nucleons in \({ }_3^7 \mathrm{Li}\) is 7.
The number of nucleons in \({ }_2^4 \mathrm{He}\) is 4.
The total binding energy of the reactants (lithium and hydrogen) is calculated as follows:
For \({ }_3^7 \mathrm{Li}\) :
Total Binding Energy of Li \(=\) Binding Energy per Nucleon \(\times \text { Number of Nucleons }=5.60 \mathrm{MeV} \times 7=39.2 MeV\)
For \({ }_1^1 \mathrm{H}:\)
Total Binding Energy of \(\mathrm{H}=0 \mathrm{MeV}\) (since H has no binding energy)
Thus, the total binding energy of the reactants is:
Total Binding Energy of Reactants \(=39.2 \mathrm{MeV}+0 \mathrm{MeV}=39.2 \mathrm{MeV}\)
The total binding energy of the products (two \({ }_2^4 \mathrm{He}\) nuclei) is calculated as follows:
Total Binding Energy of Products \(=2 \times \text { Binding Energy per Nucleon of } \mathrm{He} \times \text { Number of Nucleons in } \mathrm{He}=2 \times 7.06 \mathrm{MeV} \times 4\)
\(
=56.48 \mathrm{MeV}
\)
The energy \(Q\) released in the reaction can be calculated using the difference in binding energies:
\(Q=\) Total Binding Energy of Products – Total Binding Energy of ReactantsSubstituting the values:
\(
Q=56.48 \mathrm{MeV}-39.2 \mathrm{MeV}=17.28 \mathrm{MeV}
\)
Thus, the value of energy \(Q\) released is approximately 17.3 MeV. -
Question 16 of 83
16. Question
A certain mass of hydrogen is changed to Helium by the process of fusion. The mass defect in the fusion reaction is 0.02866 u . The energy liberated per nucleon is: (given \(1 \mathrm{u}=931 \mathrm{MeV}\) ) [AIPMT 2013]
CorrectIncorrectHint
(b) Given
Mass defect \(=0.2886 u\)
Total energy liberated \(=0.2886 \times 931 \mathrm{MeV}=26.86 \mathrm{MeV}\)
We have been asked the energy liberated per unit mass
atomic mass of helium \(=4 \mathrm{u}\)
So, Energy liberated per unit mass \(=26.86 \mathrm{MeV} / 4\)
\(
=6.675 \mathrm{MeV}
\) -
Question 17 of 83
17. Question
How does the binding energy per nucleon vary with the increase in the number of nucleons? [NEET Kar. 2013]
CorrectIncorrectHint
(d) From the graph of BE/A versus mass number A it is clear that, BE/A first increases and then decreases with increase in mass number.
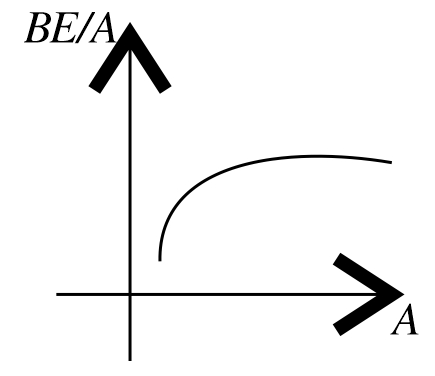
-
Question 18 of 83
18. Question
If the nuclear radius of \({ }^{27} \mathrm{Al}\) is 3.6 Fermi, the approximate nuclear radius of \({ }^{64} \mathrm{Cu}\) in Fermi is: [AIPMT 2012]
CorrectIncorrectHint
(c) The radius of the nuclears is directly proportional to cube root of atomic number i.e. \(R \propto A^{1 / 3}\)
\(R=R_0 A^{1 / 3}\), where \(R_0\) is a constant of proportionality
\(
\frac{R_2}{R_1}=\left(\frac{A_2}{A_1}\right)^{1 / 3} \Rightarrow\left(\frac{64}{27}\right)^{1 / 3}=\frac{4}{3}
\)
where \(R_1=\) the radius of \({ }^{27} \mathrm{Al}\), and \(A_1=\) Atomic mass number of \(A 1\) \(R_2=\) the radius of \({ }^{64} \mathrm{Cu}\) and \(A_2=\) Atomic mass number of Cu
\(
R_2=3.6 \times \frac{4}{3}=4.8 \mathrm{~m}
\) -
Question 19 of 83
19. Question
The power obtained in a reactor using \(\mathrm{U}^{235}\) disintegration is 1000 kW . The mass decay of \(\mathrm{U}^{235}\) per hour is approximately equal to: [AIPMT 2011]
CorrectIncorrectHint
(b) The energy released is the product of power and time:
\(E=P \times t\)
\(E=10^6 \mathrm{~W} \times 3600 \mathrm{~s}\)
\(E=3.6 \times 10^9 \mathrm{~J}\)Step 2: Using \(E=m c^2\), solve for \(m\) :
\(m=\frac{E}{c^2}\)
\(m=\frac{3.6 \times 10^9 \mathrm{~J}}{\left(3 \times 10^8 \mathrm{~m} / \mathrm{s}\right)^2}\)
\(m=\frac{3.6 \times 10^9}{9 \times 10^{16}} \mathrm{~kg}\)
\(m=4 \times 10^{-8} \mathrm{~kg}\)Step 3: Convert kilograms to micrograms:
\(m=4 \times 10^{-8} \mathrm{~kg} \times \frac{10^3 \mathrm{~g}}{1 \mathrm{~kg}} \times \frac{10^6 \mu \mathrm{~g}}{1 \mathrm{~g}}\)
\(m=40 \mu \mathrm{~g}\)
The mass decay of \(\mathrm{U}^{235}\) per hour is approximately \(40 \mu \mathrm{~g}\). -
Question 20 of 83
20. Question
Fusion reaction takes place at high temperature because [AIPMT 2011]
CorrectIncorrectHint
(c) At high temperatures, the atoms have a lot of kinetic energy, which allows them to move fast enough to overcome the electrostatic repulsion between the positively charged nuclei, enabling them to get close enough to fuse together.
-
Question 21 of 83
21. Question
A nucleus of mass \(M\) emits a photon of frequency \(\nu\) and the nucleus recoils. The recoil energy will be [AIPMT 2011]
CorrectIncorrectHint
(b) Momentum
\(
\mathrm{Mu}=\frac{\mathrm{E}}{\mathrm{c}}=\frac{\mathrm{h} \nu}{\mathrm{c}}
\)
Recoil energy
\(
\frac{1}{2} \mathrm{Mu}^2=\frac{1}{2} \frac{\mathrm{M}^2 \mathrm{u}^2}{\mathrm{M}}=\frac{1}{2 \mathrm{M}}\left(\frac{\mathrm{~h} \nu}{\mathrm{c}}\right)^2=\frac{\mathrm{h}^2 \nu^2}{2 \mathrm{Mc}^2}
\) -
Question 22 of 83
22. Question
A nucleus \({ }_n^m \mathrm{X}\) emits one \(\alpha\)-particle and two \(\beta\)-particle The resulting nucleus is: [AIPMT 2011]
CorrectIncorrectHint
(a) When an alpha particle \(\left({ }_2^4 \mathrm{He}\right)\) is emitted, the mass number and the mass number and the atomic number of the daughter nucleus decreases by four and two respectively. When a beta particle \(\left(\beta^{-}\right)\)is emitted, the atomic number of the daughter nucleus increases by one but the mass number remains the same.
\(
\therefore \quad{ }_n^m X \xrightarrow{\alpha}{ }_{n-2}^{m-4} Y \xrightarrow{2 \beta^{-}}{ }_n^{m-4} X
\) -
Question 23 of 83
23. Question
The mass of a \({ }_3^7 \mathrm{Li}\) nucleus is 0.042 u less than the sum of the masses of all its nucleons. The binding energy per nucleon of the \({ }_3^7 \mathrm{Li}\) nucleus is near: [AIPMT 2010]
CorrectIncorrectHint
(b) Here, \(\Delta m=0.042 a . m . u\)
\(
\begin{aligned}
& \mathrm{BE}=\Delta m \times 931.5 \mathrm{MeV} \\
& =0.042 \times 931.5 \mathrm{MeV}=39.123 \mathrm{MeV} \\
& \text { Number of nucleons in }{ }_3^7 L i \text { is } 7 \text {. } \\
& \mathrm{BE} / \text { nucleon }=\frac{39.123}{7}\simeq 5.6 \mathrm{MeV}
\end{aligned}
\) -
Question 24 of 83
24. Question
The binding energy per nucleon in deuterium and helium nuclei are 1.1 MeV and 7.0 MeV , respectively. When two deuterium nuclei fuse to form a helium nucleus the energy released in the fusion is: [AIPMT 2010]
CorrectIncorrectHint
(d) Binding energy of two \({ }_1 H^2\) nuclei
\(
=2(1.1 \times 2)=4.4 \mathrm{MeV}
\)
Binding energy of one \({ }_2 \mathrm{He}^4\) nucelus
\(
\begin{aligned}
& =4 \times 7.0=28 \mathrm{MeV} \\
& \therefore \text { Energy released in fusion }=28-4.4=23.6 \mathrm{MeV}
\end{aligned}
\) -
Question 25 of 83
25. Question
The number of beta particles emitted by a radioactive substance is twice the number of alpha particles emitted by it. The resulting daughter is an: [AIPMT 2009]
CorrectIncorrectHint
(c) Given that:
Initially, the radioactive element has undergone \(\alpha\)-decay and then \(\beta\)-decay
No: of \(\beta\) particles \(=2 \times\) No: of \(\alpha\) particles
Radioactive decay is as follows:
\(1 \alpha\)-decay: \({ }_Z^A \mathrm{X} \rightarrow{ }_{Z-4}^{A-4} \mathrm{Y}+{ }_2^4 \alpha\)
\(2 \beta\)-decay: \({ }_{Z-2}^{A-4} \mathrm{Y} \rightarrow{ }_{Z-1}^{A-4} \mathrm{Y} \rightarrow{ }_Z^{A-4} \mathrm{Y}\)
The daughter nucleus after \(\alpha\)-decay has its mass number reduced by 4.
There will be no change in the reduced mass number after \(\beta\)-decay.
The obtained daughter nucleus has a different mass number \(=(A-4)\) and the same atomic number \(=\mathrm{Z}\) as the parent nucleus.
Therefore, the resulting daughter is an isotope of the parent. -
Question 26 of 83
26. Question
If \(M(A, Z), M_p\), and \(M_n\) denote the masses of the nucleus \({ }_Z^A X\), proton, and neutron respectively in units of \(u\left(1 u=931.5 \mathrm{MeV} / \mathrm{c}^2\right)\) and represent its binding energy \((B E)\) in MeV. Then: [AIPMT 2008]
CorrectIncorrectHint
(a)
\(
\text { Mass defect }={ZM}_{{p}}+({A}-{Z}) {M}_{{n}}-{M}({~A}, {Z})
\)
\(
\text { B. E. }=\left[Z M_p+(A-Z) M_n-M(A, Z)\right] c^2
\)
\(
\therefore \frac{B . E .}{c^2}=Z M_p+(A-Z) M_n-M(A, Z)
\)
\(
M(A, Z)=Z M_p+(A-Z) M_n-B . E . / c^2
\) -
Question 27 of 83
27. Question
Two nuclei have their mass numbers in the ratio of \(1: 3\). The ratio of their nuclear densities would be: [AIPMT 2008]
CorrectIncorrectHint
(d) The radius of a nucleus is given by \(r=r_0 A^{\frac{1}{3}}\), where \(r_0\) is a constant and \(A\) is the mass number.
The volume of a sphere is given by \(V=\frac{4}{3} \pi r^3\).
Density is defined as mass per unit volume: \(\rho=\frac{m}{V}\).
Nuclear density is approximately constant for all nuclei.
Let \(A_1\) and \(A_2\) be the mass numbers of the two nuclei. Given \(\frac{A_1}{A_2}=\frac{1}{3}\).
The radii of the nuclei are \(r_1=r_0 A_1^{\frac{1}{3}}\) and \(r_2=r_0 A_2^{\frac{1}{3}}\).
The ratio of the radii is \(\frac{r_1}{r_2}=\frac{r_0 A_1^{\frac{1}{3}}}{r_0 A_2^{\frac{1}{3}}}=\left(\frac{A_1}{A_2}\right)^{\frac{1}{3}}=\left(\frac{1}{3}\right)^{\frac{1}{3}}\).
The volumes of the nuclei are \(v_1=\frac{4}{3} \pi r_1^3\) and \(v_2=\frac{4}{3} \pi r_2^3\).
The ratio of the volumes is \(\frac{V_1}{V_2}=\frac{\frac{4}{3} \pi r_1^3}{\frac{4}{3} \pi r_2^3}=\left(\frac{r_1}{r_2}\right)^3=\left(\left(\frac{1}{3}\right)^{\frac{1}{3}}\right)^3=\frac{1}{3}\).
The densities of the nuclei are \(\rho_1=\frac{m_1}{V_1}\) and \(\rho_2=\frac{m_2}{V_2}\).
Since the mass of a nucleus is proportional to its mass number, we can write \(m_1=k A_1\) and \(m_2=k A_2\), where \(k\) is a constant.
The ratio of the densities is \(\frac{\rho_1}{\rho_2}=\frac{\frac{m_1}{V_1}}{\frac{m_2}{V_2}}=\frac{m_1}{m_2} \cdot \frac{V_2}{V_1}=\frac{A_1}{A_2} \cdot \frac{V_2}{V_1}=\frac{1}{3} \cdot \frac{3}{1}=1\).
The ratio of the nuclear densities is \(1: 1\). -
Question 28 of 83
28. Question
If the nucleus \({ }_{13}^{27} \mathrm{Al}\) has nuclear radius of about 3.6 fm , then \({ }_{32}^{125} \mathrm{Te}\) would have its radius approximately as [AIPMT 2007]
CorrectIncorrectHint
(d) It has been known that a nucleus of mass number \(A\) has radius
\(
R=R_0 A^{1 / 3},
\)
where \(R_0=1.2 \times 10^{-15} \mathrm{~m}\)
and \(A=\) mass number
In case of \({ }_{13}^{27} \mathrm{~A}\), let nuclear radius be \(R_1\)
and for \({ }_{32}^{125} \mathrm{Te}\), nuclear radius be \(R_2\)
For \({ }_{13}^{27} \mathrm{Al}, R_1=R_0(27)^{1 / 3}=3 R_0\)
For \({ }_{32}^{125} \mathrm{Te}, R_2=R_0(125)^{1 / 3}=5 R_0\)
\(
\frac{R_2}{R_1}=\frac{5 R_0}{3 R_0}=\frac{5}{3} R_1=\frac{5}{3} \times 3.6=6 \mathrm{fm}
\) -
Question 29 of 83
29. Question
In the radioactive decay process, the negatively charged emitted \(\beta\)-particles are: [AIPMT 2007]
CorrectIncorrectHint
(b) Beta decay can involve the emission of either electrons or positrons. The electrons or positrons emitted in a \(\beta\)-decay do not exist inside the nucleus. They are only created at the time of emission, just as photons are created when an atom makes a transition from higher to a lower energy state.
In negative \(\beta\)-decay a neutron in the nucleus is transformed into a proton, an electron and an antineutrino.
Hence, in radioactive decay process. the negatively charged emitted \(\beta\)-particles are the electrons produced as a result of the decay of neutrons present inside the nucleus. -
Question 30 of 83
30. Question
A nucleus \({ }_Z X^A\) has a mass represented by \(M(A, Z)\). If \(M_P\) and \(M_n\) denote the mass of proton and neutron respectively and BE the binding energy, then: [AIPMT 2007]
CorrectIncorrectHint
(b) The difference in mass of a nucleus and its constituents, \(\Delta M\), is called the mass defect and is given by
\(
\begin{aligned}
& \Delta M=\left[Z M_p+(A-Z) M_n\right]-M \\
& \text { and binding energy }=\Delta M c^2 \\
& =\left[\left\{Z M_p+(A-Z) M_n\right\}-M\right] c^2
\end{aligned}
\) -
Question 31 of 83
31. Question
The binding energy of deuteron is 2.2 MeV and that of \({ }_2 \mathrm{He}^4\) is 28 MeV . If two deuterons are fused to form one \({ }_2 \mathrm{He}^4\), then the energy released is:
CorrectIncorrectHint
(b) Binding energy of deuteron: 2.2 MeV
Binding energy of \({ }_2 \mathrm{He}^4: 28 \mathrm{MeV}\)
The binding energy of one deuteron is 2.2 MeV.
The total binding energy of two deuterons is \(2 \times 2.2 \mathrm{MeV}=4.4 \mathrm{MeV}\).
The energy released is the difference between the binding energy of \({ }_2 \mathrm{He}^4\) and the total binding energy of the two deuterons.
Energy released \(=28 \mathrm{MeV}-4.4 \mathrm{MeV}=23.6 \mathrm{MeV}\).
The energy released is 23.6 MeV. -
Question 32 of 83
32. Question
The radius of germanium \((\mathrm{Ge})\) nuclide is measured to be twice the radius of \({ }_4^9 \mathrm{Be}\). The number of nucleons in Ge are [AIPMT 2006]
CorrectIncorrectHint
(c) We use the formula,
\(
R=R_0 A^{1 / 3}
\)
This represents relation between atomic mass and radius of the nucleus.
For berillium,
\(
R_1=R_0(9)^{1 / 3}
\)
For germanium,\(\quad R_2=R_0 A^{1 / 3}\)
\(
\begin{aligned}
& \frac{R_1}{R_2}=\frac{(9)^{1 / 3}}{(A)^{1 / 3}} \Rightarrow \frac{1}{2}=\frac{(9)^{1 / 3}}{(A)^{1 / 3}} \\
& \Rightarrow \frac{1}{8}=\frac{9}{A} \Rightarrow A=8 \times 9=72
\end{aligned}
\) -
Question 33 of 83
33. Question
Fission of nuclei is possible because the binding energy per nucleon in them [AIPMT 2005]
CorrectIncorrectHint
(d) The binding energy per nucleon for the middle nuclides (from \(A=20 \rightarrow A=56\) ) is maximum. Hence, these are more stable.
As the mass number increases, the binding energy per nucleon gradually decreases and ultimately binding energy per nucleon of heavy nuclides (such as uranium, etc) is comparatively low. Hence, these nuclides are relatively unstable. So, they can be fissioned easily.
-
Question 34 of 83
34. Question
In any fission process, the ratio \(\frac{\text { mass of fission products }}{\text { mass of parent nucleus }}\) is [AIPMT 2005]
CorrectIncorrectHint
(c) Binding energy per nucleon for fission products is higher relative to Binding energy per nucleon for parent nucleus, i.e., more masses are lost and are obtained as kinetic energy of fission products. So, the given ratio \(<1\).
-
Question 35 of 83
35. Question
In the reaction \({ }_1^2 \mathrm{H}+{ }_1^3 \mathrm{H} \longrightarrow{ }_2^4 \mathrm{He}+{ }_0^1 n\), if the binding energies of \({ }_1^2 \mathrm{H},{ }_1^3 \mathrm{H}\) and \({ }_2^4 \mathrm{H}\) He are respectively \(a, b\) and \(c\) (in MeV , then the energy (in MeV ) released in this reaction is: [AIPMT 2005]
CorrectIncorrectHint
(c) Binding energy of \({ }_1^2 \mathrm{H}\) is \(a~ \mathrm{MeV}\).
Binding energy of \({ }_1^3 \mathrm{H}\) is \(b~ \mathrm{MeV}\).
Binding energy of \({ }_2^4 \mathrm{He}\) is \(c~ \mathrm{MeV}\).
The total binding energy of the reactants is the sum of the binding energies of \({ }_1^2 \mathrm{H}\) and \({ }_1^3 \mathrm{H}\).
\(
E_{\text {reactants }}=a+b
\)
The total binding energy of the products is the binding energy of \({ }_2^4 \mathrm{He}\).
\(
E_{\text {products }}=c
\)
The energy released is the difference between the binding energies of the products and the reactants.
\(
\begin{aligned}
& Q=E_{\text {products }}-E_{\text {reactants }} \\
& Q=c-(a+b) \\
& Q=c-a-b
\end{aligned}
\)
The energy released in the reaction is \(c-a-b \mathrm{MeV}\). -
Question 36 of 83
36. Question
\(M_p\) denotes the mass of a proton and \(M_n\) that of a neutron. A given nucleus, of binding energy \(B\), contains \(Z\) protons and \(N\) neutrons. The mass \(M(N, Z)\) of the nucleus is given by: [AIPMT 2004]
( \(c\) is the velocity of light )CorrectIncorrectHint
(b) Step 1: Understand the Binding Energy
The binding energy \(B\) of a nucleus is the energy required to disassemble the nucleus into its constituent protons and neutrons. It can be expressed in terms of the mass of the nucleus and the masses of the individual nucleons (protons and neutrons).Step 2: Write the Mass of Constituent Particles
The total mass of the individual nucleons (protons and neutrons) in the nucleus can be calculated as:
Total mass of nucleons \(=Z \cdot M_p+N \cdot M_n\)
where \(M_p\) is the mass of a proton and \(M_n\) is the mass of a neutron.
Step 3: Relate Binding Energy to Mass
The binding energy \(B\) can be related to the mass defect (the difference between the mass of the individual nucleons and the mass of the nucleus) by the equation:
\(
B=(\text { mass of nucleons })-(\text { mass of nucleus }) \cdot c^2
\)
Rearranging this gives us:
\(
B=\left(Z \cdot M_p+N \cdot M_n-M(N, Z)\right) \cdot c^2
\)
Step 4: Solve for the Mass of the Nucleus
Rearranging the equation for \(M(N, Z)\) :
\(
M(N, Z)=Z \cdot M_p+N \cdot M_n-\frac{B}{c^2}
\)
Final Expression
Thus, the mass of the nucleus can be expressed as:
\(
M(N, Z)=Z \cdot M_p+N \cdot M_n-\frac{B}{c^2}
\) -
Question 37 of 83
37. Question
A nucleus represented by the symbol \({ }_Z^A \mathrm{X}\) has: [AIPMT 2004]
CorrectIncorrectHint
(a) \({ }_Z^A \mathrm{X}\) has number of protons \(=Z\) and
number of neutrons \(N=A-Z\) where \(A\) is the total number of protons and neutron,
i.e., \(A=Z+N\). -
Question 38 of 83
38. Question
If in nuclear fusion process the masses of the fusing nuclei be \(m_1\) and \(m_2\) and the mass of the resultant nucleus be \(m_3\), then [AIPMT 2004]
CorrectIncorrectHint
(d) \(m_1\) and \(m_2\) are the masses of the fusing nuclei.
\(m_3\) is the mass of the resultant nucleus.
In nuclear fusion, mass is converted into energy according to Einstein’s equation \(E=m c^2\).
The mass of the resultant nucleus is less than the sum of the masses of the fusing nuclei.
In nuclear fusion, a small amount of mass is converted into energy.
This means that the mass of the resultant nucleus is less than the sum of the masses of the fusing nuclei.
\(
m_3<m_1+m_2
\) -
Question 39 of 83
39. Question
A nuclear reaction is given by;
\(
{ }_Z^A \mathrm{X} \rightarrow{ }_{Z+1}^A \mathrm{Y}+{ }_{-1}^0 \mathrm{e}+\nu
\)
represents: [AIPMT 2003]CorrectIncorrectHint
(a)
\(
\text { Nuclear reaction equation: }{ }_Z^A \mathrm{X} \rightarrow{ }_{Z+1}^A \mathrm{Y}+{ }_{-1}^0 \mathrm{e}+\nu
\)
\(\beta\)-decay involves the emission of an electron (or positron) and a neutrino (or antineutrino).
\(\gamma\)-decay involves the emission of a gamma ray photon.
Fusion involves the combining of two or more atomic nuclei to form a heavier nucleus.
Fission involves the splitting of an atomic nucleus into two or more lighter nuclei.
The equation shows a nucleus X transforming into a nucleus Y , an electron \({ }_{-1}^0 \mathrm{e}\), and a neutrino \(\nu\).
The atomic number \(Z\) increases by 1 , while the mass number \(A\) remains the same.
\(\beta\)-decay involves the emission of an electron or a positron. \(\gamma\)-decay involves the emission of a gamma ray photon. Fusion involves combining nuclei.
Fission involves splitting a nucleus.
The emission of an electron and a neutrino, along with the increase in atomic number by 1 while the mass number remains the same, is characteristic of \(\beta\)-decay. -
Question 40 of 83
40. Question
The mass number of a nucleus is: [AIPMT 2003]
CorrectIncorrectHint
(c) Mass number of an element is the total number of protons and neutrons present inside the atomic nucleus of the element. It is represented by A, A is different for different elements. Mass number of a nucleus is sometimes equal to its atomic number,for example in case of hydrogen, number of neutrons= 0. So, mass number = atomic number.
-
Question 41 of 83
41. Question
The mass of a proton is 1.0073 u and that of a neutron is 1.0087 u ( \(\mathrm{u}=\) atomic mass unit). The binding energy of \({ }_2^4 \mathrm{He}\) is: (Given: helium nucleus mass \(\approx 4.0015 \mathrm{u})\) [AIPMT 2003]
CorrectIncorrectHint
(c) Mass of proton: \(m_p=1.0073 \mathrm{u}\)
Mass of neutron: \(m_n=1.0087 \mathrm{u}\)
Mass of Helium-4 nucleus: \(m_{H e}=4.0015 \mathrm{u}\)
Helium- 4 has 2 protons and 2 neutrons.
\(
1 \mathrm{u}=931.5 \frac{\mathrm{MeV}}{c^2}
\)
Binding energy formula: \(E_b=\Delta m c^2\), where \(\Delta m\) is the mass defect.
Mass defect formula: \(\Delta m=\left(Z m_p+N m_n\right)-m_{\text {nucleus }}\), where \(Z\) is the number of protons, \(N\) is the number of neutrons, and \(m_{\text {nucleus }}\) is the mass of the nucleus.
Total mass of protons: \(2 \times m_p=2 \times 1.0073 \mathrm{u}=2.0146 \mathrm{u}\)
Total mass of neutrons: \(2 \times m_n=2 \times 1.0087 \mathrm{u}=2.0174 \mathrm{u}\)
Total mass of nucleons: \(2.0146 \mathrm{u}+2.0174 \mathrm{u}=4.032 \mathrm{u}\)
\(
\text { Mass defect: } \Delta m=\left(2 m_p+2 m_n\right)-m_{H e}=4.032 \mathrm{u}-4.0015 \mathrm{u}=0.0305 \mathrm{u}
\)
\(
\text { Binding energy: } E_b=\Delta m \times 931.5 \frac{\mathrm{MeV}}{c^2} \times c^2=0.0305 \mathrm{u} \times 931.5 \frac{\mathrm{MeV}}{\mathrm{u}}=28.40075 \mathrm{MeV}
\)
\(
\text { The binding energy of the Helium-4 nucleus is approximately } 28.4 \mathrm{MeV} \text {. }
\) -
Question 42 of 83
42. Question
Which of the following rays are not electromagnetic waves? [AIPMT 2003]
CorrectIncorrectHint
(c) Cosmic rays, \(\gamma\)-rays, and \(X\)-rays are part of electromagnetic spectrum, while \(\beta\)-rays are emitted by radioactive elements. Hence \(\beta\)-rays is not electromagnetic waves.
-
Question 43 of 83
43. Question
The volume occupied by an atom is greater than the volume of the nucleus by a factor of about: [AIPMT 2003]
CorrectIncorrectHint
(d) Radius of atom \(r_a \approx 10^{-10} \mathrm{~m}\).
Radius of nucleus \(r_n \approx 10^{-15} \mathrm{~m}\).
Volume of a sphere is \(V=\frac{4}{3} \pi r^3\).
The volume of the atom is:
\(V_a=\frac{4}{3} \pi r_a^3\)
\(V_a=\frac{4}{3} \pi\left(10^{-10} \mathrm{~m}\right)^3\)
\(\quad V_a=\frac{4}{3} \pi \cdot 10^{-30} \mathrm{~m}^3\)
The volume of the nucleus is:
\(V_n=\frac{4}{3} \pi r_n^3\)
\(V_n=\frac{4}{3} \pi\left(10^{-15} \mathrm{~m}\right)^3\)
\(V_n=\frac{4}{3} \pi \cdot 10^{-45} \mathrm{~m}^3\)
The ratio of the volume of the atom to the volume of the nucleus is:
\(\frac{V_a}{V_n}=\frac{\frac{4}{3} \pi \cdot 10^{-30} \mathrm{~m}^3}{\frac{4}{3} \pi \cdot 10^{-45} \mathrm{~m}^3}\)
\(\frac{V_a}{V_n}=\frac{10^{-30}}{10^{-45}}\)
\(\frac{V_a}{V_n}=10^{-30-(-45)}\)
\(\frac{V_a}{V_n}=10^{15}\)The volume occupied by an atom is greater than the volume of the nucleus by a factor of about \(10^{15}\).
-
Question 44 of 83
44. Question
Solar energy is mainly caused due to [AIPMT 2003]
CorrectIncorrectHint
(d) As a result of fusion, enormous amount of heat is liberated which is the main cause of source of solar energy.
-
Question 45 of 83
45. Question
If a deuteron is bombarded on a \({ }_8 \mathrm{O}^{16}\) nucleus then an \(\alpha\)-particle is emitted. The product nucleus is: [AIPMT 2002]
CorrectIncorrectHint
(d) Deuteron: \({ }_{\mathrm{1}} \mathrm{H}^2\)
Oxygen-16 nucleus: \({ }_8 \mathrm{O}^{16}\)
Alpha particle: \({ }_2 \mathrm{He}^4\)
The reaction is: \({ }_1 \mathrm{H}^2+{ }_8 \mathrm{O}^{16} \rightarrow{ }_2 \mathrm{He}^4+{ }_z \mathrm{X}^A\)
Where \({ }_Z \mathrm{X}^{\boldsymbol{A}}\) is the unknown product nucleus.The total mass number on the left side is \(2+16=18\).
The total mass number on the right side is \(4+A\).
Therefore, \(18=4+A\), so \(A=18-4=14\).The total atomic number on the left side is \(1+8=9\).
The total atomic number on the right side is \(2+Z\).
Therefore, \(9=2+Z\), so \(Z=9-2=7\).With \(A=14\) and \(Z=7\), the product nucleus is \({ }_7 \mathrm{~N}^{14}\).
The product nucleus is nitrogen-14. -
Question 46 of 83
46. Question
Which of the following are suitable for the fusion process? [AIPMT 2002]
CorrectIncorrectHint
(a) For nuclear fusion process the nuclei with low mass are suitable.
-
Question 47 of 83
47. Question
If a \({ }_a^b \mathrm{X}\) species emits firstly a positron, then two \(\alpha\) and two \(\beta\) and at last one \(\alpha\) is also emitted and finally converted into stable \({ }_d^c \mathrm{Y}\) species, so the correct relation will be: [AIPMT 2001]
CorrectIncorrectHint
(a) Initial nucleus \({ }_a^b X\)
Decays:
Positron emission
Two \(\alpha\) particles emission
Two \(\beta\) particles emission
One \(\alpha[l/atex] particle emissionFinal nucleus [latex]{ }_d^c \mathrm{Y}\)
\(
\text { Positron emission: }{ }_1^1 \mathrm{e} \rightarrow{ }_{-1}^0 \mathrm{e}+{ }_{\mathrm{p}}^1 \mathrm{1} \text { (atomic number decreases by } 1 \text { ) }
\)
\(\alpha\) particle emission: \({ }_2^4 \mathrm{He}\) (atomic number decreases by 2 , mass number decreases by 4)
\(\beta\) particle emission: \({ }_0^{\mathrm{1}} \mathrm{n} \rightarrow{ }_1^1 \mathrm{p}+{ }_{-1}^0 \mathrm{e}\) (atomic number increases by 1 )
Positron emission:
Change in atomic number: \(a-1\)
Change in mass number: \(b-0\)
\(\alpha\) particle emission (2 times):
Change in atomic number: \(a-4\)
Change in mass number: \(b-8\)
\(\beta\) particle emission (2 times):
Change in atomic number: \(a+2\)
Change in mass number: \(b-0\)
\(\alpha\) particle emission (1 time):
Change in atomic number: \(a-2\)
Change in mass number: \(b-4\)
Total change in atomic number: \(a-1-4+2-2=a-5\)
Total change in mass number: \(b-8-4=b-12\)
The final nucleus is \({ }_{a-5}^{b-12} \mathrm{Y}\)
\(
\begin{aligned}
& c=b-12 \\
& d=a-5
\end{aligned}
\)
Compare the result with the options
The correct relation is \(c=b-12, d=a-5\). -
Question 48 of 83
48. Question
The energy released in nuclear fission is due to: [AIPMT 2001]
CorrectIncorrectHint
(b) In nuclear fission, some mass is converted into energy, and the total binding energy \((\mathrm{BE})\) of the fragments is greater than the BE of the parental element. This difference in \(B E\) represents the energy released in the fission process.
-
Question 49 of 83
49. Question
\(M_n\) and \(M_p\) represent the mass of the neutron and proton respectively. An element having mass \(M\) has \(N\) neutrons and \(Z\)-protons, then the correct relation will be: [AIPMT 2001]
CorrectIncorrectHint
(a) Given : Mass of neutron \(=M_n\)
Mass of proton \(=M_p\); Atomic mass of the element \(=M\); Number ofneutrons in the element \(=N\) and number of protons in the element \(=Z\).
We know that the atomic mass ( \(M\) ) of any stable nucleus is always less than the sum of the masses of the constituent particles.
Therefore, \(M<\left[N M_n+Z M_p\right]\).
\(X\) is a neutrino, when \(\beta\)-particle is emitted. -
Question 50 of 83
50. Question
If \(\mathrm{X}(n, \alpha)\) converts into \({ }_3^7 L i\), then X will be: [AIPMT 2001]
CorrectIncorrectHint
(a) Nuclear reaction: \(\mathrm{X}(n, \alpha) \rightarrow{ }_3^7 \mathrm{Li}\)
\(n\) represents a neutron: \({ }_0^1 n\)
\(\alpha\) represents an alpha particle (Helium nucleus): \({ }_2^4 \mathrm{He}\)
Lithium isotope: \({ }_3^7 \mathrm{Li}\)
Write the complete nuclear reaction equation.
\(
\mathrm{X}+{ }_0^1 n \rightarrow{ }_3^7 \mathrm{Li}+{ }_2^4 \mathrm{He}
\)
\(
\begin{aligned}
&\text { Let the mass number of } \mathrm{X} \text { be } A \text {. }\\
&\begin{aligned}
& A+1=7+4 \\
& A=7+4-1 \\
& A=10
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
&\text { Let the atomic number of } \mathrm{X} \text { be } \boldsymbol{Z} \text {. }\\
&\begin{aligned}
& Z+0=3+2 \\
& Z=3+2 \\
& Z=5
\end{aligned}
\end{aligned}
\)
The element with atomic number 5 is Boron (B). Therefore, X is \({ }_5^{10} B\).
The unknown element X is Boron- 10. -
Question 51 of 83
51. Question
Which rays contain (+ve) charged particle: [AIPMT 2001]
CorrectIncorrectHint
(b) \(\alpha \text {-rays are positively charged particles }\)
-
Question 52 of 83
52. Question
Nuclear-fission is best explained by: [AIPMT 2000]
CorrectIncorrectHint
(a) Nuclear fission is best explained by the Liquid Droplet Model, while the Yukawa $\pi$-meson theory explains the nuclear force. The Independent Particle Model describes the nucleus as a collection of nucleons. The Proton-Proton cycle describes the fusion of hydrogen in the sun.
According to liquid drop model of nucleus, an excited nucleus breaks into lighter nuclei just like an excited drop breaks into tiny drops.
-
Question 53 of 83
53. Question
For the given reaction, the particle X is:
\({ }_6^{11} \mathrm{C} \rightarrow{ }_5^{11} \mathrm{~B}+\beta^{+}+\mathrm{X}\) [AIPMT 2000]CorrectIncorrectHint
(c) The charge on the left side is +6.
The charge on the right side is +5 from Boron and +1 from positron, totaling +6 . Therefore, the charge of \(X\) is 0.
The lepton number on the left side is 0.
The lepton number of the positron ( \(\beta^{+}\)) is -1.
To balance the lepton number, X must have a lepton number of +1.
A particle with charge 0 and lepton number +1 is a neutrino \(\left(v_e\right)\).The unknown particle X is a neutrino.
-
Question 54 of 83
54. Question
If a radioactive element emitted one \(\alpha\) and one \(\beta\)-particle, then the mass number of the daughter element is: [AIPMT 1999]
CorrectIncorrectHint
(a) Emission of \(1 \alpha\) particle led to decrease in atomic number by 2 while mass number by 4. On the other hand, emission of \(2 \beta\) particles increases atomic number by 2. Hence, overall emission of, \(1 \alpha\) and \(2 \beta\) particles led to decrease in mass number by 4.
-
Question 55 of 83
55. Question
Alpha-particles are [AIPMT 1999]
CorrectIncorrectHint
(d) We know that alpha particles are the nucleus of ionized helium atoms which contain two protons and two neutrons. These are emitted by the nuclei of certain radioactive substances. Streams of alpha particles, called $\alpha$-rays, produce intense ionisation in gases through which they pass and are easily absorbed by matter.
-
Question 56 of 83
56. Question
The explosion of the atomic bomb takes place due to [AIPMT 1999]
CorrectIncorrectHint
(a) The explosion of an atomic bomb takes place due to nuclear fission.
Explanation:
Nuclear fission:
This is the process where a heavy atom’s nucleus splits into smaller fragments, releasing a large amount of energy. This is the primary mechanism behind the explosion of an atomic bomb. -
Question 57 of 83
57. Question
In nuclear reactions, we have the conservation of [AIPMT 2000]
CorrectIncorrectHint
(d) Nuclear reactions follow all law of Conservation principles.
-
Question 58 of 83
58. Question
Atomic weight of Boron is 10.81 and it has two isotopes \({ }_5 B^{10}\) and \({ }_5 B^{11}\). Then the ratio \({ }_5 B^{10}:{ }_5 B^{11}\) in nature would be [AIPMT 1998]
CorrectIncorrectHint
(a) Suppose that,
The number of \({ }^{10} B\) type atoms \(=x\)
and the number of \({ }^{11} B\) type atoms \(=y\)
Weight of \({ }^{10} B\) type atoms \(=10 x\)
Weight of \({ }^{11} B\) type atoms \(=11 y\)
Total number of atoms \(=x+y\)
\(
\begin{aligned}
& \therefore \text { Atomic weight }=\frac{10 x+11 y}{x+y}=10.81 \\
& \Rightarrow 10 x+11 y=10.81 x+10.81 y \\
& \Rightarrow 0.81 x=0.19 y \Rightarrow \frac{x}{y}=\frac{19}{81}
\end{aligned}
\)Note: If relative abundance of isotopes in an element has ratio \(n_1: n_2\) whose atomic massers are \(m_1\) and \(m_2\) then atomic masses of elements is \(M=\frac{n_1 m_1+n_2 m_2}{n_1+n_2}\).
-
Question 59 of 83
59. Question
For the nuclear reaction:
\(
{ }_{92}^{235} \mathrm{U}+{ }_0^1 \mathrm{n} \rightarrow{ }_{56}^{144} \mathrm{Ba}+\ldots+3{ }_0^1 \mathrm{n}
\)
The blank space can be filled by: [AIPMT 1998]CorrectIncorrectHint
(b)
\(
\text { Nuclear reaction: }{ }_{92}^{235} \mathrm{U}+{ }_0^1 \mathrm{n} \rightarrow{ }_{56}^{144} \mathrm{Ba}+\mathrm{X}+3{ }_0^1 \mathrm{n}
\)
The total mass number on the left side is \(235+1=236\).
The total mass number on the right side is \(144+3 \times 1=147\).
The mass number of the unknown element X is \(236-147=89\).
The total atomic number on the left side is \(92+0=92\).
The total atomic number on the right side is \(56+3 \times 0=56\).
The atomic number of the unknown element X is \(92-56=36\).The element with atomic number 36 is Krypton (Kr). Therefore, the missing element X is \({ }_{36}^{89} \mathrm{Kr}\).
The missing element is Krypton-89. -
Question 60 of 83
60. Question
\({ }_n X^m\) emitted one \(\alpha\) and \(2 \beta\) particles, then it will become : [AIPMT 1998]
CorrectIncorrectHint
(c) An alpha particle is a helium nucleus, which consists of 2 protons and 2 neutrons. Therefore, when an alpha particle is emitted from the nucleus \({ }_n^m X\) :
The mass number decreases by 4 (because 2 protons and 2 neutrons are lost).
The atomic number decreases by 2 (because 2 protons are lost).
So, after emitting one alpha particle, the new nucleus will be:
\(
{ }_n^m X \rightarrow_{n-2}^{m-4} Y
\)
A beta particle is essentially an electron, which is emitted when a neutron in the nucleus is converted into a proton. Each beta particle emission results in:
The mass number remaining the same (since a neutron is converted to a proton).
The atomic number increases by 1 (since a proton is added).
Since two beta particles are emitted, the changes will be:
The mass number remains \(m-4\).
The atomic number increases by 2 ( 1 for each beta particle).
So, after emitting two beta particles from the nucleus \({ }_{n-2}^{m-4} Y\) :
\(
{ }_{n-2}^{m-4} Y \rightarrow{ }_{(n-2)+2}^{m-4} Z
\)
This simplifies to:
\(
{ }_n^{m-4} Z
\)
After both emissions, the resulting nucleus is:
\(
{ }_n^{m-4} Z
\)
Final Result:
The resulting nucleus after the emission of one alpha particle and two beta particles from the original nucleus \({ }_n^m X[latex] is:
[latex]
{ }_n^{m-4} Z
\) -
Question 61 of 83
61. Question
When \(\mathrm{X} \rightarrow{ }_7^{14} \mathrm{~N}+2 \beta^{-}\)then the number of neutrons in X will be: [AIPMT 1998]
CorrectIncorrectHint
(d) From the given information, we know that after two beta emissions, the nucleus becomes \({ }_7^{14} N\) :
Atomic number \((Z)=7\)
Mass number \((A)=14\)
Since each beta emission increases the atomic number by 1 , we can deduce the atomic number of the parent nucleus \(X\) :
After 1 beta emission: Atomic number \(=7-1=6\)
After 2 beta emissions: Atomic number \(=6-1=5\)Thus, the atomic number of the parent nucleus \(X\) is 5 .
The mass number remains unchanged during beta decay. Therefore, the mass number of the parent nucleus \(X\) is the same as that of the final nucleus:
Mass number of \(X=14\)
The number of neutrons can be calculated using the formula:
Number of Neutrons = Mass Number – Atomic NumberSubstituting the values we have:
Number of Neutrons \(=14-5=9\)
The number of neutrons in the parent nucleus \(X\) is 9. -
Question 62 of 83
62. Question
The stable nucleus that has a radius half that of \(\mathrm{Fe}^{56}\) is [AIPMT 1997]
CorrectIncorrectHint
(a) The nuclear radius \(R=R_0 A^{1 / 3}\)
or \(R \propto A^{1 / 3}\)
\(
\begin{aligned}
& \text { or, } R^3 \propto A \Rightarrow A \propto R^3 \\
& \therefore \frac{A_2}{A_1}=\left(\frac{R_2}{R_1}\right)^3=\left(\frac{R_1 / 2}{R_1}\right)^3=\frac{1}{8} \\
& A_2=\frac{A_1}{8}=\frac{56}{8}=7
\end{aligned}
\)
Thus, stable nucleus will be \(L i^7\) -
Question 63 of 83
63. Question
In a fission reaction
\(
{ }_{92}^{236} U \rightarrow{ }^{117} X+{ }^{117} Y+n+n
\)
the binding energy per nucleon of \(X\) and \(Y\) is 8.5 MeV whereas of \({ }^{236} U\) is 7.6 MeV. The total energy liberated will be about [AIPMT 1997]CorrectIncorrectHint
(b) The binding energy per nucleon of \({ }^{236} U\) is given as 7.6 MeV .
The binding energy per nucleon of \(X\) and \(Y\) is given as 8.5 MeV .
The total number of nucleons in \(X\) and \(Y\) is:
\(
117+117=234 \text { nucleons }
\)
\(
\begin{aligned}
& \text { The total binding energy for } X \text { and } Y \text { is: } \\
& \text { Total Binding Energy }{ }_{X+Y} \\
& =\text { Binding Energy per Nucleon } \times \text { Total Nucleons } \\
& =8.5 \mathrm{MeV} \times 234=1989 \mathrm{MeV}
\end{aligned}
\)
The total binding energy for \({ }^{236} U\) is:
Total Binding Energy \({ }_U=7.6 \mathrm{MeV} \times 236=1793.6 MeV\)
The energy liberated \((\Delta E)\) is the difference between the total binding energy of the products and the original nucleus:
\(
\Delta E=\text { Total Binding Energy }{ }_{X+Y}
\)
Total Binding Energy \({ }_U\)
\(
\Delta E=1989 \mathrm{MeV}-1793.6 \mathrm{MeV}=195.4 \mathrm{MeV}
\)
Thus, in per fission of Uranium nearly 200 MeV (we rounded 195.4 to 200) energy is liberated -
Question 64 of 83
64. Question
Complete the equation for the following fission process : \({ }_{92} U^{235}+{ }_0 \mathrm{n}^1 \rightarrow{ }_{38} S^{90}+\ldots\) [AIPMT 1998]
CorrectIncorrectHint
(a) Balance the mass number
The total mass number on the left side is \(235+1=236\).
The mass number of Strontium is 90.
Let the mass number of the unknown element be \(A\) and the number of neutrons be \(x\).The equation for mass number balance is \(236=90+A+x \cdot 1\).
The total atomic number on the left side is \(92+0=92\).
The atomic number of Strontium is 38.
Let the atomic number of the unknown element be \(\boldsymbol{Z}\).
The equation for atomic number balance is \(92=38+Z\).
From the atomic number balance equation: \(Z=92-38=54\). The element with atomic number 54 is Xenon ( \(X e\) ).
From the mass number balance equation: \(236=90+A+x\).
We know that fission of Uranium-235 typically releases 3 neutrons, so let \(x=3\).
Then, \(236=90+A+3\).
Solving for \(A: A=236-90-3=143\).
The complete equation is \({ }_{92} U^{235}+{ }_0 n^1 \rightarrow{ }_{38} S r^{90}+{ }_{54} X e^{143}+3_0 n^1\) -
Question 65 of 83
65. Question
Which of the following is used as a moderator in nuclear reactors? [AIPMT 1997]
CorrectIncorrectHint
(c) A moderator in a nuclear reactor slows down neutrons, making them more likely to cause fission. Heavy water (D2O) is commonly used as a moderator because its deuterium atoms effectively slow down neutrons.
-
Question 66 of 83
66. Question
A nucleus ruptures into twonuclear parts, which have their velocity ratio equal to \(2: 1\). What will be the ratio of their nuclear size (nuclear radius)? [AIPMT 1996]
CorrectIncorrectHint
(b) Applying law of conservation of momentum,
\(
\begin{aligned}
& m_1 v_1=m_2 v_2 \\
& \frac{v_1}{v_2}=\frac{m_2}{m_1}
\end{aligned}
\)
\(
\text { As } \mathrm{m}=\frac{4}{3} \pi r^3 \rho \Rightarrow m \propto r^3
\)
Hence, \(\frac{m_2}{m_1}=\frac{r_2^3}{r_1^3}\)
\(
\therefore \frac{v_1}{v_2}=\frac{r_2^3}{r_1^3} \Rightarrow \frac{r_2}{r_1}=\left(\frac{1}{2}\right)^{\frac{1}{3}}
\) -
Question 67 of 83
67. Question
The mass number of a nucleus is equal to the number of [AIPMT 1995]
CorrectIncorrectHint
(b) Mass number (A) is the total number of protons \((Z)\) and neutrons \((N)\) in an atomic nucleus.
\(
A=Z+N
\)
Protons and neutrons are collectively called nucleons.
Therefore, the mass number is the number of nucleons.The mass number of a nucleus is equal to the number of nucleons it contains.
-
Question 68 of 83
68. Question
The mass number of He is 4 and that for sulphur is 32. The radius of sulphur nuclei is larger than that of helium by [AIPMT 1994]
CorrectIncorrectHint
\(
\text { (c) } \frac{R_S}{R_{H e}}=\left(\frac{A_S}{A_{H e}}\right)^{1 / 3}=\left(\frac{32}{4}\right)^{1 / 3}=2
\) -
Question 69 of 83
69. Question
If the binding energy per nucleon in \({ }_3 \mathrm{Li}^7\) and \({ }_2 \mathrm{He}^4\) nuclei are respectively 5.60 MeV and 7.06 MeV, then the energy of proton in the reaction \({ }_3 \mathrm{Li}^7+p \rightarrow 2{ }_2 \mathrm{He}^4\) is [AIPMT 1994]
CorrectIncorrectHint
(d) Calculate the total binding energy of \({ }_3 \mathrm{Li}^7\):
The number of nucleons in \({ }_3 \mathrm{Li}^7\) is 7.
The total binding energy of \({ }_3 \mathrm{Li}^7\) is \(7 \times 5.60 \mathrm{MeV}=39.2 \mathrm{MeV}\).
The number of nucleons in \({ }_2 \mathrm{He}^4\) is 4.
The total binding energy of \(2_2 \mathrm{He}^4\) is \(2 \times 4 \times 7.06 \mathrm{MeV}=56.48 \mathrm{MeV}\).
The energy released is the difference between the total binding energy of the products and the reactants.
Energy released \(=56.48 \mathrm{MeV}-39.2 \mathrm{MeV}=17.28 \mathrm{MeV}\).
Rounding to one decimal place, the energy released is 17.3 MeV. -
Question 70 of 83
70. Question
Heavy water is used as a moderator in a nuclear reactor. The function of the moderator is [AIPMT 1994]
CorrectIncorrectHint
(d) The function of a moderator in a nuclear reactor is to slow down neutrons to thermal energies.
Explanation: A moderator like heavy water is used to reduce the speed of fastmoving neutrons produced during fission, allowing them to be more effectively captured by uranium-235 nuclei and sustain the chain reaction.
-
Question 71 of 83
71. Question
Energy released in the fission of a single \({ }_{92}^{235} \mathrm{U}\) nucleus is 200 MeV . The fission rate of a \({ }_{92}^{235} \mathrm{U}\) filled reactor operating at a power level of 5 W is [AIPMT 1993]
CorrectIncorrectHint
\(
\begin{aligned}
&\text { (b) Fission rate }\\
&\begin{aligned}
& =\frac{\text { total power }}{\frac{\text { energy }}{\text { fission }}}=\frac{5}{200 \times 1.6 \times 10^{-13}} \\
& =1.56 \times 10^{11} \mathrm{~s}^{-1}
\end{aligned}
\end{aligned}
\) -
Question 72 of 83
72. Question
The nucleus which has radius one-third of the radius of \(\mathrm{Cs}^{189}\) is [AIPMT 1993]
CorrectIncorrectHint
(b) \(\text { The radius of } \mathrm{Cs}^{189} \text { is } R_{C s}=R_0(189)^{\frac{1}{3}} \text {. }\)
The radius of the unknown nucleus is \(R_x=\frac{1}{3} R_{C s}\). \(R_x=\frac{1}{3} R_0(189)^{\frac{1}{3}}\).
\(
\begin{aligned}
&\text { Let the mass number of the unknown nucleus be } A_x \text {. }\\
&\begin{aligned}
& R_x=R_0\left(A_x\right)^{\frac{1}{3}} \\
& R_0\left(A_x\right)^{\frac{1}{3}}=\frac{1}{3} R_0(189)^{\frac{1}{3}} \\
& \left(A_x\right)^{\frac{1}{3}}=\frac{1}{3}(189)^{\frac{1}{3}}
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
A_x & =\frac{1}{27} \cdot 189 . \\
A_x & =7
\end{aligned}
\)
The nucleus with mass number 7 is \({ }_3^7 \mathrm{Li}\). -
Question 73 of 83
73. Question
The mass density of a nucleus varies with mass number A as [AIPMT 1992]
CorrectIncorrectHint
(c) The nuclear radius \(r\) varies with mass number A according to the relation
\(
\begin{aligned}
& r \propto A^{1 / 3} \text { or } A \propto r^3 \\
& \text { density }=\frac{\text { mass }}{\text { volume }}
\end{aligned}
\)
Further, mass \(\propto \mathrm{A}\) and volume \(\propto r^3\)
\(
\therefore \frac{\text { mass }}{\text { volume }}=\text { constant }
\) -
Question 74 of 83
74. Question
Solar energy is due to [AIPMT 1992]
CorrectIncorrectHint
(a) Solar energy is due to fusion reaction.
Explanation: In the Sun’s core, hydrogen atoms fuse together to form helium, releasing a vast amount of energy, which is what we perceive as solar energy. -
Question 75 of 83
75. Question
The energy equivalent of one atomic mass unit is [AIPMT 1992]
CorrectIncorrectHint
(c) \(1 \text { a.m.u= } 931 \mathrm{MeV}\)
-
Question 76 of 83
76. Question
An electron with (rest mass \(\mathrm{m}_0\) ) moves with a speed of 0.8 c. Its mass when it moves with this speed is [AIPMT 1991]
CorrectIncorrectHint
(c) \(\text { Relativistic mass formula: } m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\)
\(
\frac{m_0}{\sqrt{\frac{c^2-(0.8 c)^2}{c^2}}}=\frac{5 m_0}{3}
\) -
Question 77 of 83
77. Question
If the nuclear force between two protons, two neutrons and between proton and neutron is denoted by \(F_{p p}, F_{n n}\) and \(F_{p n}\) respectively, then [AIPMT 1991]
CorrectIncorrectHint
(c) The nuclear force is charge-independent.
Therefore, the nuclear force between any two nucleons is the same.
\(
F_{p p}=F_{n n}=F_{p n}
\)
The nuclear forces between two protons, two neutrons, and a proton and neutron are approximately equal. -
Question 78 of 83
78. Question
The constituents of atomic nuclei are believed to be [AIPMT 1991]
CorrectIncorrectHint
(a) Nucleus contains only neutrons and protons.
-
Question 79 of 83
79. Question
In the nucleus of \({ }_{11} \mathrm{Na}^{23}\), the number of protons, neutrons and electrons are [AIPMT 1991]
CorrectIncorrectHint
(a) \(Z=11\) i.e., number of protons \(=11, A=23\)
\(\therefore\) Number of neutrons \(=A-Z=12\)
Number of electron \(=0\) (No electron in nucleus)
Therefore \(11,12,0\). -
Question 80 of 83
80. Question
The nuclei \({ }_6 \mathrm{C}^{13}\) and \({ }_7 \mathrm{~N}^{14}\) can be described as [AIPMT 1990]
CorrectIncorrectHint
(a) The number of neutrons is the mass number minus the atomic number.
\(
N=13-6=7
\)
The number of neutrons is the mass number minus the atomic number.
\(
N=14-7=7
\)
Compare the number of neutrons:
Both nuclei have 7 neutrons.
They have different numbers of protons ( 6 and 7). Therefore, they are isotones.The nuclei \({ }_6 \mathrm{C}^{13}\) and \({ }_7 \mathrm{~N}^{14}\) are isotones
-
Question 81 of 83
81. Question
The ratio of the radii of the nuclei \({ }_{13} A l^{27}\) and \({ }_{52} T e^{125}\) is approximately [AIPMT 1990]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (a) } \quad R \propto(A)^{1 / 3} \\
& \therefore R_{A l} \propto(27)^{1 / 3} \text { and } R_{T e} \propto(125)^{1 / 3} \\
& \therefore \frac{R_{A l}}{R_{T e}}=\frac{3}{5}=\frac{6}{10}
\end{aligned}
\) -
Question 82 of 83
82. Question
Which of the following statements is true for nuclear forces? [AIPMT 1990]
CorrectIncorrectHint
(c) Nuclear forces are short range attractive forces which balance the repulsive forces between the protons inside the nucleus.
Explanation: Nuclear forces are indeed short-range, attractive forces that act between nucleons (protons and neutrons) within the nucleus. These forces are strong enough to overcome the electrostatic repulsion between positively charged protons, holding the nucleus together.
-
Question 83 of 83
83. Question
The average binding energy of a nucleon inside an atomic nucleus is about [AIPMT 1989]
CorrectIncorrectHint
(a) Average B.E./nucleon in nuclei is of the order of 8 MeV .