12.2 Alpha-particle Scattering and Rutherford’s Nuclear Model of Atom

At the suggestion of Ernst Rutherford, in 1911, H. Geiger and E. Marsden performed some experiments. In one of their experiments, as shown in Fig. 12.1, they directed a beam of \(5.5 \mathrm{MeV} \alpha\)-particles emitted from a \({ }_{83}^{214} \mathrm{Bi}\) radioactive source at a thin metal foil made of gold.

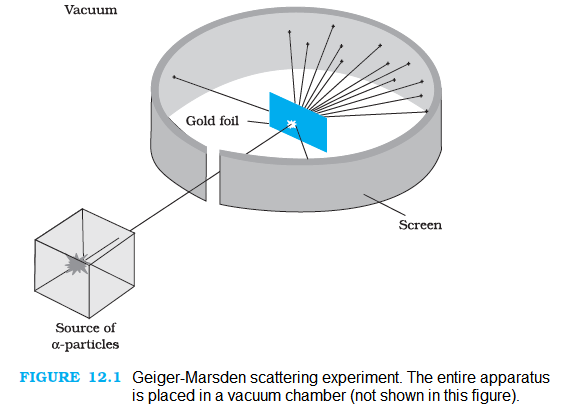
Figure 12.2 shows a schematic diagram of this experiment. Alpha-particles emitted by a \({ }_{83}^{214} \mathrm{Bi}\) radioactive source were collimated into a narrow beam by their passage through lead bricks. The beam was allowed to fall on a thin foil of gold of thickness \(2.1 \times 10^{-7} \mathrm{~m}\). The scattered alpha-particles were observed through a rotatable detector consisting of zinc sulphide screen and a microscope. The scattered alpha-particles on striking the screen produced brief light flashes or scintillations. These flashes may be viewed through a microscope and the distribution of the number of scattered particles may be studied as a function of angle of scattering.

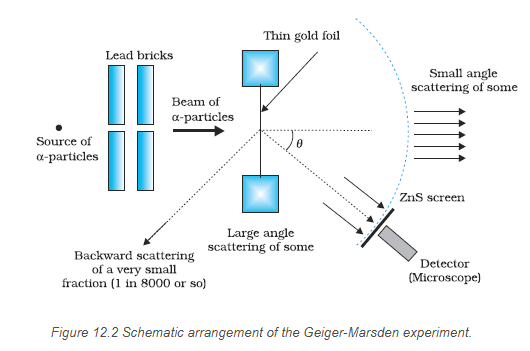
A typical graph of the total number of \(\alpha\)-particles scattered at different angles, in a given interval of time, is shown in Fig. 12.3. The dots in this figure represent the data points and the solid curve is the theoretical prediction based on the assumption that the target atom has a small, dense, positively charged nucleus. Many of the \(\alpha\)-particles pass through the foil. It means that they do not suffer any collisions. Only about \(0.14 \%\) of the incident \(\alpha\)-particles scatter by more than \(1^{\circ}\); and about 1 in 8000 deflect by more than \(90^{\circ}\). Rutherford argued that, to deflect the \(\alpha\)-particle backwards, it must experience a large repulsive force. This force could be provided if the greater part of the mass of the atom and its positive charge were concentrated tightly at its centre. Then the incoming \(\alpha\)-particle could get very close to the positive charge without penetrating it, and such a close encounter would result in a large deflection. This agreement supported the hypothesis of the nuclear atom. This is why Rutherford is credited with the discovery of the nucleus.

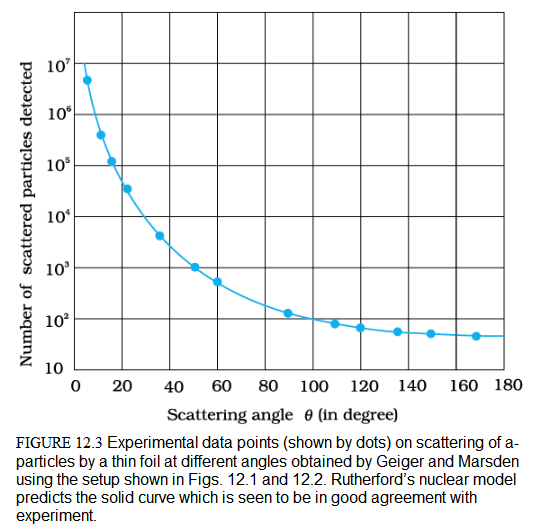
In Rutherford’s nuclear model of the atom, the entire positive charge and most of the mass of the atom are concentrated in the nucleus with the electrons some distance away. The electrons would be moving in orbits about the nucleus just as the planets do around the sun. Rutherford’s experiments suggested the size of the nucleus to be about \(10^{-15} \mathrm{~m}\) to \(10^{-14} \mathrm{~m}\). From kinetic theory, the size of an atom was known to be \(10^{-10} \mathrm{~m}\), about 10,000 to 100,000 times larger than the size of the nucleus (see Chapter 10, Section 10.6 in Class XI Physics textbook). Thus, the electrons would seem to be at a distance from the nucleus of about 10,000 to 100,000 times the size of the nucleus itself. Thus, most of an atom is empty space. With the atom being largely empty space, it is easy to see why most \(\alpha\)-particles go right through a thin metal foil. However, when \(\alpha\)-particle happens to come near a nucleus, the intense electric field there scatters it through a large angle. The atomic electrons, being so light, do not appreciably affect the \(\alpha\)-particles.

The scattering data shown in Fig. 12.3 can be analysed by employing Rutherford’s nuclear model of the atom. As the gold foil is very thin, it can be assumed that \(\alpha\)-particles will suffer not more than one scattering during their passage through it. Therefore, computation of the trajectory of an alpha particle scattered by a single nucleus is enough. Alpha particles are nuclei of helium atoms and, therefore, carry two units, \(2 e\), of positive charge and have the mass of the helium atom. The charge of the gold nucleus is \(Z e\), where \(Z\) is the atomic number of the atom; for gold \(Z=79\). Since the nucleus of gold is about 50 times heavier than an \(\alpha\)-particle, it is reasonable to assume that it remains stationary throughout the scattering process. Under these assumptions, the trajectory of an alpha-particle can be computed employing Newton’s second law of motion and Coulomb’s law for electrostatic force of repulsion between the alpha-particle and the positively charged nucleus.

The magnitude of this force is
\(
F=\frac{1}{4 \pi \varepsilon_0} \frac{(2 e)(Z e)}{r^2} \dots(12.1)
\)
where \(r\) is the distance between the \(\alpha\)-particle and the nucleus. The force is directed along the line joining the \(\alpha\)-particle and the nucleus. The magnitude and direction of the force on an \(\alpha\)-particle continuously changes as it approaches the nucleus and recedes away from it.

12.2.1 Alpha-particle trajectory

The trajectory traced by an \(\alpha\)-particle depends on the impact parameter, \(b\) of collision. The impact parameter is the perpendicular distance of the initial velocity vector of the \(\alpha\)-particle from the centre of the nucleus (Fig.12.4). A given beam of \(\alpha\)-particles has a distribution of impact parameters \(b\), so that the beam is scattered in various directions with different probabilities (Fig. 12.4). (In a beam, all particles have nearly same kinetic energy.) It is seen that an \(\alpha\)-particle close to the nucleus (small impact parameter) suffers large scattering. In case of head-on collision, the impact parameter is minimum and the \(\alpha\)-particle rebounds back \((\theta \cong \pi)\). For a large impact parameter, the \(\alpha\)-particle goes nearly undeviated and has a small deflection \((\theta \cong 0)\).

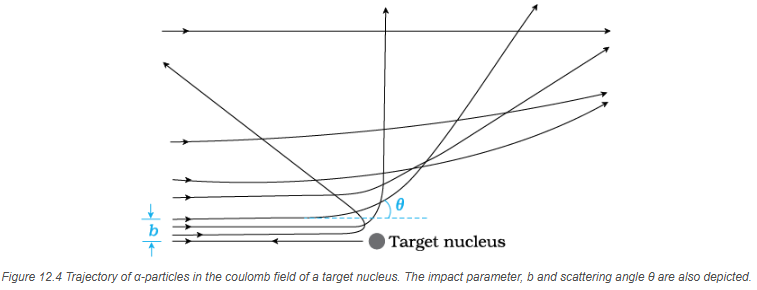
The fact that only a small fraction of the number of incident particles rebound back indicates that the number of \(\alpha\)-particles undergoing head on collision is small. This, in turn, implies that the mass and positive charge of the atom is concentrated in a small volume. Rutherford scattering, therefore, is a powerful way to determine an upper limit to the size of the nucleus.

Example 12.1: In the Rutherford’s nuclear model of the atom, the nucleus (radius about \(10^{-15} \mathrm{~m}\) ) is analogous to the sun about which the electron move in orbit (radius \(\approx 10^{-10} \mathrm{~m}\) ) like the earth orbits around the sun. If the dimensions of the solar system had the same proportions as those of the atom, would the earth be closer to or farther away from the sun than actually it is? The radius of earth’s orbit is about \(1.5 \times 10^{11} \mathrm{~m}\). The radius of sun is taken as \(7 \times 10^8 \mathrm{~m}\).

Solution: The ratio of the radius of electron’s orbit to the radius of nucleus is \(\left(10^{-10} \mathrm{~m}\right) /\left(10^{-15} \mathrm{~m}\right)=10^5\), that is, the radius of the electron’s orbit is \(10^5\) times larger than the radius of nucleus. If the radius of the earth’s orbit around the sun were \(10^5\) times larger than the radius of the sun, the radius of the earth’s orbit would be \(10^5 \times 7 \times 10^8 \mathrm{~m}=\) \(7 \times 10^{13} \mathrm{~m}\). This is more than 100 times greater than the actual orbital radius of earth. Thus, the earth would be much farther away from the sun.
It implies that an atom contains a much greater fraction of empty space than our solar system does.

Example 12.2: In a Geiger-Marsden experiment, what is the distance of closest approach to the nucleus of a \(7.7 \mathrm{MeV} \alpha\)-particle before it comes momentarily to rest and reverses its direction?

Solution: The key idea here is that throughout the scattering process, the total mechanical energy of the system consisting of an \(\alpha\)-particle and a gold nucleus is conserved. The system’s initial mechanical energy is \(E_i\), before the particle and nucleus interact, and it is equal to its mechanical energy \(E_f\) when the \(\alpha\)-particle momentarily stops. The initial energy \(E_i\) is just the kinetic energy \(K\) of the incoming \(\alpha\) – particle. The final energy \(E_f\) is just the electric potential energy \(U\) of the system. The potential energy \(U\) can be calculated from Eq. (12.1).
Let \(d\) be the centre-to-centre distance between the \(\alpha\)-particle and the gold nucleus when the \(\alpha\)-particle is at its stopping point. Then we can write the conservation of energy \(E_i=E_f\) as
\(
\begin{aligned}
&K=\frac{1}{4 \pi \varepsilon_0} \frac{(2 e)(Z e)}{d}=\frac{2 Z e^2}{4 \pi \varepsilon_0 d}\\
&\text { Thus the distance of closest approach } d \text { is given by }\\
&d=\frac{2 Z e^2}{4 \pi \varepsilon_0 K}
\end{aligned}
\)
The maximum kinetic energy found in \(\alpha\)-particles of natural origin is 7.7 MeV or \(1.2 \times 10^{-12} \mathrm{~J}\). Since \(1 / 4 \pi \varepsilon_0=9.0 \times 10^9 \mathrm{~N} \mathrm{~m}^2 / \mathrm{C}^2\). Therefore with \(e=1.6 \times 10^{-19} \mathrm{C}\), we have,
\(
\begin{aligned}
d & =\frac{(2)\left(9.0 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2\right)\left(1.6 \times 10^{-19} \mathrm{C}\right)^2 \mathrm{Z}}{1.2 \times 10^{-12} \mathrm{~J}} \\
& =3.84 \times 10^{-16} \mathrm{Z} \mathrm{~m}
\end{aligned}
\)
The atomic number of foil material gold is \(Z=79\), so that \(d(\mathrm{Au})=3.0 \times 10^{-14} \mathrm{~m}=30 \mathrm{fm} .\left(1 \mathrm{fm}\right.\) (i.e. fermi) \(\left.=10^{-15} \mathrm{~m}.\right)\)
The radius of gold nucleus is, therefore, less than \(3.0 \times 10^{-14} \mathrm{~m}\). This is not in very good agreement with the observed result as the actual radius of gold nucleus is 6 fm. The cause of discrepancy is that the distance of closest approach is considerably larger than the sum of the radii of the gold nucleus and the \(\alpha\)-particle. Thus, the \(\alpha\)-particle reverses its motion without ever actually touching the gold nucleus.

12.2.2 Electron orbits

The Rutherford nuclear model of the atom which involves classical concepts, pictures the atom as an electrically neutral sphere consisting of a very small, massive, and positively charged nucleus at the centre surrounded by the revolving electrons in their respective dynamically stable orbits. The electrostatic force of attraction, \(F_e\) between the revolving electrons and the nucleus provides the requisite centripetal force \(\left(F_c\right)\) to keep them in their orbits. Thus, for a dynamically stable orbit in a hydrogen atom
\(
\begin{gathered}
\stackrel{F}{e}=F_c \\
\frac{1}{4 \pi \varepsilon_0} \frac{e^2}{r^2}=\frac{m v^2}{r} \dots(12.2)
\end{gathered}
\)
Thus the relation between the orbit radius and the electron velocity is
\(
r=\frac{e^2}{4 \pi \varepsilon_0 m v^2} \dots(12.3)
\)
The kinetic energy \((K)\) and electrostatic potential energy \((U)\) of the electron in hydrogen atom are
\(
K=\frac{1}{2} m v^2=\frac{e^2}{8 \pi \varepsilon_0 r} \text { and } U=-\frac{e^2}{4 \pi \varepsilon_0 r}
\)
(The negative sign in \(U\) signifies that the electrostatic force is in the \(-r\) direction.) Thus the total energy \(E\) of the electron in a hydrogen atom is
\(
\begin{aligned}
E=K+U & =\frac{e^2}{8 \pi \varepsilon_0 r}-\frac{e^2}{4 \pi \varepsilon_0 r} \\
& =-\frac{e^2}{8 \pi \varepsilon_0 r} \dots(12.4)
\end{aligned}
\)
The total energy of the electron is negative. This implies the fact that the electron is bound to the nucleus. If \(E\) were positive, an electron will not follow a closed orbit around the nucleus.

Example 12.3: It is found experimentally that 13.6 eV energy is required to separate a hydrogen atom into a proton and an electron. Compute the orbital radius and the velocity of the electron in a hydrogen atom.

Solution: Total energy of the electron in hydrogen atom is \(-13.6 \mathrm{eV}=\) \(-13.6 \times 1.6 \times 10^{-19} \mathrm{~J}=-2.2 \times 10^{-18} \mathrm{~J}\). Thus from Eq. (12.4), we have
\(
E=-\frac{e^2}{8 \pi \varepsilon_0 r}=-2.2 \times 10^{-18} \mathrm{~J}
\)
This gives the orbital radius
\(
\begin{aligned}
r & =-\frac{e^2}{8 \pi \varepsilon_0 E}=-\frac{\left(9 \times 10^9 \mathrm{~N} \mathrm{~m}^2 / \mathrm{C}^2\right)\left(1.6 \times 10^{-19} \mathrm{C}\right)^2}{(2)\left(-2.2 \times 10^{-18} \mathrm{~J}\right)} \\
& =5.3 \times 10^{-11} \mathrm{~m} .
\end{aligned}
\)
The velocity of the revolving electron can be computed from Eq. (12.3) with \(m=9.1 \times 10^{-31} \mathrm{~kg}\),
\(
v=\frac{e}{\sqrt{4 \pi \varepsilon_0 m r}}=2.2 \times 10^6 \mathrm{~m} / \mathrm{s}
\)