4.5 Magnetic Field on the Axis of a Circular Current Loop

In this section, we shall evaluate the magnetic field due to a circular coil along its axis. The evaluation entails summing up the effect of infinitesimal current elements $(I \mathrm{~d} l)$ mentioned in the previous section. We assume that the current $I$ is steady and that the evaluation is carried out in free space (i.e., vacuum).

Fig. 4.9 depicts a circular loop carrying a steady current $I$. The loop is placed in the $y-z$ plane with its centre at the origin $O$ and has a radius $R$. The $x$-axis is the axis of the loop. We wish to calculate the magnetic field at the point P on this axis. Let $x$ be the distance of $P$ from the centre $O$ of the loop.

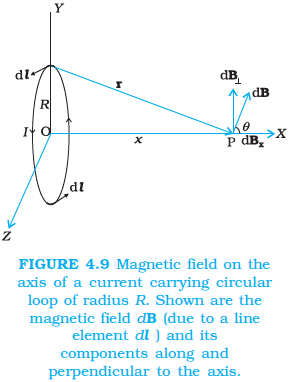
Consider a conducting element $\mathrm{d} \boldsymbol{l}$ of the loop. This is shown in Fig. 4.9. The magnitude $d B$ of the magnetic field due to $\mathrm{d} l$ is given by the Biot-Savart law [Eq. 4.11 (a)],
$d B=\frac{\mu_0}{4 \pi} \frac{I|d \boldsymbol{l} \times \mathbf{r}|}{r^3} \dots(4.12)$
Now $r^2=x^2+R^2$. Further, any element of the loop will be perpendicular to the displacement vector from the element to the axial point. For example, the element $\mathrm{d} \boldsymbol{l}$ in Fig. 4.9 is in the $y$-z plane, whereas, the displacement vector $\mathbf{r}$ from $\mathrm{d} \boldsymbol{l}$ to the axial point P is in the $x-y$ plane. Hence $|d \boldsymbol{l} \times \mathbf{r}|=r d l$. Thus,
$\mathrm{d} B=\frac{\mu_0}{4 \pi} \frac{I \mathrm{~d} l}{\left(x^2+R^2\right)} \dots(4.13)$
The direction of dB is shown in Fig. 4.9. It is perpendicular to the plane formed by $\mathrm{d} \boldsymbol{l}$ and $\mathbf{r}$. It has an $x$-component $\mathrm{d} \mathbf{B}_x$ and a component perpendicular to $x$-axis, $\mathrm{d} \mathbf{B}_{\perp}$. When the components perpendicular to the $x$-axis are summed over, they cancel out and we obtain a null result. For example, the $\mathrm{d} \mathbf{B}_{\perp}$ component due to $\mathrm{d} l$ is cancelled by the contribution due to the diametrically opposite $\mathrm{d} \boldsymbol{l}$ element, shown in Fig. 4.9. Thus, only the $x$-component survives. The net contribution along $x$-direction can be obtained by integrating $\mathrm{d} B_x=\mathrm{d} B \cos \theta$ over the loop. For Fig. 4.9,
$\cos \theta=\frac{R}{\left(x^2+R^2\right)^{1 / 2}} \dots(4.14)$
From Eqs. (4.13) and (4.14),
$\mathrm{d} B_x=\frac{\mu_0 I \mathrm{~d} l}{4 \pi} \frac{R}{\left(x^2+R^2\right)^{3 / 2}}$
The summation of elements $\mathrm{d} l$ over the loop yields $2 \pi R$, the circumference of the loop. Thus, the magnetic field at P due to entire circular loop is
$\mathbf{B}=B_x \hat{\mathbf{i}}=\frac{\mu_0 I R^2}{2\left(x^2+R^2\right)^{3 / 2}} \hat{\mathbf{i}} \dots(4.15)$
As a special case of the above result, we may obtain the field at the centre of the loop. Here $x=0$, and we obtain,
$\mathbf{B}_0=\frac{\mu_0 I}{2 R} \hat{\mathbf{i}} \dots(4.16)$
The magnetic field lines due to a circular wire form closed loops and are shown in Fig. 4.10. The direction of the magnetic field is given by (another) right-hand thumb rule stated below:

Curl the palm of your right hand around the circular wire with the fingers pointing in the direction of the current. The right-hand thumb gives the direction of the magnetic field.

Example 4.6: A straight wire carrying a current of 12 A is bent into a semi-circular arc of radius 2.0 cm as shown in Fig. 4.11(a). Consider the magnetic field $\mathbf{B}$ at the centre of the arc. (a) What is the magnetic field due to the straight segments? (b) In what way the contribution to B from the semicircle differs from that of a circular loop, and in what way does it resemble? (c) Would your answer be different if the wire were bent into a semi-circular arc of the same radius but in the opposite way as shown in Fig. 4.11 (b)?

Solution: (a) $\mathrm{d} \mathbf{l}$ and $\mathbf{r}$ for each element of the straight segments are parallel. Therefore, $\mathrm{d} \boldsymbol{l} \times \mathbf{r}=0$. Straight segments do not contribute to $|\mathbf{B}|$.
(b) For all segments of the semicircular arc, $\mathrm{d} \boldsymbol{l} \times \mathbf{r}$ are all parallel to each other (into the plane of the paper). All such contributions add up in magnitude. Hence, the direction of $\mathbf{B}$ for a semicircular arc is given by the right-hand rule, and the magnitude is half that of a circular loop. Thus $\mathbf{B}$ is $1.9 \times 10^{-4} \mathrm{~T}$ normal to the plane of the paper going into it.
(c) Same magnitude of $\mathbf{B}$ but opposite in direction to that in (b).

Example 4.7: Consider a tightly wound 100 turn coil of radius 10 cm, carrying a current of 1 A. What is the magnitude of the magnetic field at the centre of the coil?

Solution: Since the coil is tightly wound, we may take each circular element to have the same radius $R=10 \mathrm{~cm}=0.1 \mathrm{~m}$. The number of turns $N=100$. The magnitude of the magnetic field is,
$B=\frac{\mu_0 N I}{2 R}=\frac{4 \pi \times 10^{-7} \times 10^2 \times 1}{2 \times 10^{-1}}=2 \pi \times 10^{-4}=6.28 \times 10^{-4} \mathrm{~T}$