Vectors and Scalars
In Physics, we often use the terms force, speed, velocity, and work, and these quantities are classified as a scalar or vector quantities. A scalar quantity is a physical quantity with only magnitudes, such as mass and electric charge. On the other hand, a vector quantity is a physical quantity that has both magnitudes and directions like force and weight.
What is a Scalar Quantity?
A scalar quantity is defined as the physical quantity with only magnitude and no direction. Such physical quantities can be described just by their numerical value without directions. The addition of these physical quantities follows the simple rules of algebra, and here, only their magnitudes are added.
For example, the mass of a system is described by saying that it is 5 kg. If two bodies one having a mass of 5 kg and the other having a mass of 2 kg are added together to make a composite system, the total mass of the system becomes 5 kg + 2 kg = 7 kg. Such quantities are called scalars.
Some examples of scalars include Mass, Speed, Distance, Time, Volume, Temperature, and density.
What is a Vector Quantity?
The physical quantities which have magnitude and direction and which can be added according to the triangle rule, are called vector quantities. Other examples of vector quantities are force, linear momentum, angular velocity, electric field, magnetic field, etc.
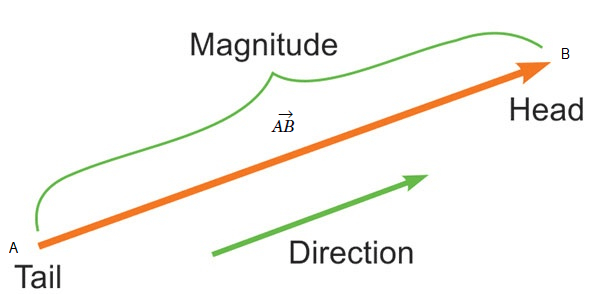
Vector Notation: The vectors are denoted by putting an arrow over the symbols representing them. Thus, we write \(\overrightarrow{A B}\), \(\overrightarrow{B C}\) etc. Sometimes a vector is represented by a single letter such as \(\vec{v}, \vec{F}\), etc. Quite often in printed books, the vectors are represented by boldface letters like AB, BC, v, f, etc.
The front end (carrying the arrow) is called the head and the rear end is called the tail. This is shown below how a vector quantity is represented.
If a physical quantity has magnitude as well as direction but does not add up according to the triangle rule, it will not be called a vector quantity. The electric current in a wire has both magnitude and direction but there is no meaning of the triangle rule there. Thus, electric current is not a vector quantity.
Equal Vectors
Two vectors (representing two values of the same physical quantity) are called equal if their magnitudes and directions are the same. The figure below shows \(\vec{A}\) and \(\vec{B}\) are equal as their magnitude and direction are the same.

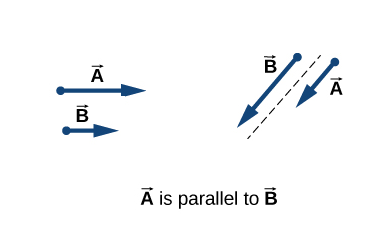
Parallel Vectors
Two vectors that have identical directions are said to be parallel vectors—meaning, they are parallel to each other. The figure below shows \(\vec{A}\) and \(\vec{B}\) are in parallel.
Antiparallel Vectors
Two vectors are said to be anti-parallel vectors if they are in opposite directions. The figure below shows \(\vec{A}\) and \(\vec{B}\) are antiparallel vectors (which is exactly opposite).

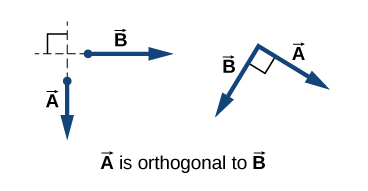
Orthogonal Vectors
Two vectors with directions perpendicular to each other are said to be orthogonal vectors. The figure below shows \(\vec{A}\) and \(\vec{B}\) are orthogonal vectors (directions differ by 90°—meaning, they are orthogonal).
Unit Vector
A vector is a quantity that has both magnitude, as well as direction. A vector that has a magnitude of 1 is a unit vector. It is also known as the Direction Vector.
Unit Vector is given by \(\hat{a}=\frac{\vec{a}}{|\vec{a}|}\)
Where \(|\vec{a}|\) indicates the magnitude of the vector \(\vec{a}\).
Components of Vectors
For the analytical method of vector addition and subtraction, we use some simple geometry and trigonometry, instead of using a ruler and protractor as we did for graphical methods. However, the graphical method will still come in handy to visualize the problem by drawing vectors using the head-to-tail method. The analytical method is more accurate than the graphical method, which is limited by the precision of the drawing. For a refresher on the definitions of the sine, cosine, and tangent of an angle, see figure-1.
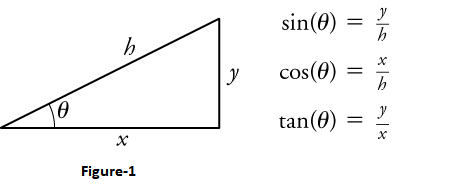
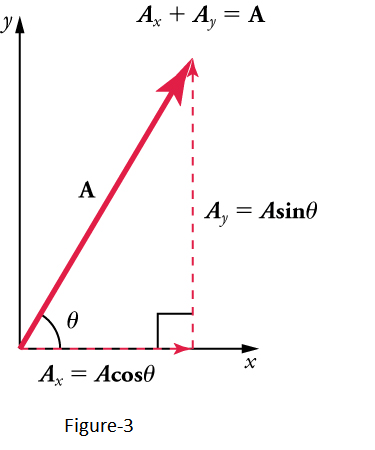
\(
\mathbf{A}_{\mathbf{x}}+\mathbf{A}_{\mathbf{y}}=\mathbf{A}
\)
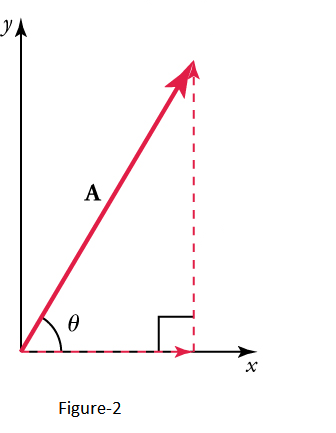
If the vector \(\mathbf{A}\) is known, then its magnitude \(A\) (its length) and its angle \(\theta\) (its direction) are known. To find \(A_x\) and \(A_y\), its \(x\) – and \(y\)-components, we use the following relationships for a right triangle:
\(
A_x=A \cos \theta
\)
and
\(
A_y=A \sin \theta
\)
where \(A_x\) is the magnitude of \(\mathbf{A}\) in the \(x\)-direction, \(A_y\) is the magnitude of \(\mathbf{A}\) in the \(y\)-direction, and \(\theta\) is the angle of the resultant with respect to the \(x\)-axis, as shown in Figure-3.
Example 2: \(\text { Find the unit vector } \vec{p} \text { for the given vector, } 12 \hat{i}-3 \hat{j}-4 \hat{k} \text {. }\)
Solution:
Let’s find the magnitude of the given vector first,
\(
|p|=\sqrt{x^2+y^2+z^2}=\sqrt{144+9+16}=\sqrt{169}=13
\)
Let’s use this magnitude to find the unit vector now:
\(
\begin{aligned}
&\hat{p}=\frac{\vec{p}}{|p|}=\frac{x \hat{i}+y \hat{j}+z \hat{k}}{\sqrt{x^2+y^2+z^2}} \\
&\hat{p}=\frac{12 \hat{i}-3 \hat{j}-4 \hat{j}}{13} \\
&\hat{p}=\frac{12}{13} \hat{i}-\frac{3}{13} \hat{j}-\frac{4}{13} \hat{k}
\end{aligned}
\)
The unit vector in Bracket form is:
\(
\hat{p}=\left(\frac{(12)}{13},-\frac{(3)}{13}, \frac{(-4)}{13}\right)
\)
Example 3: For the given vector \(p=3 \hat{i}-12 \hat{j}+\hat{4 i}\). Calculate the unit vector in the direction of the vector. Also, represent it in unit vector component format as well as the bracket format.
Solution:
Given vector: \(p=3 \hat{i}-12 \hat{j}+\hat{4} i\)
We will start with the determining the magnitude first:
\(
\begin{aligned}
&|p|=\sqrt{x^2+y^2+z^2} \\
&|p|=\sqrt{(3)^2+(-12)^2+(4)^2}=\sqrt{9+144+16}=\sqrt{169}=13
\end{aligned}
\)
If written in bracket format then the formula is:
\(
\begin{aligned}
&\hat{p}=\frac{\vec{p}}{|\vec{p}|}=\frac{x, y, z}{\sqrt{x^2+y^2+z^2}}=\left(\frac{x}{\sqrt{x^2+y^2+z^2}}, \frac{y}{\sqrt{x^2+y^2+z^2}}, \frac{z}{\sqrt{x^2+y^2+z^2}}\right) \\
&\hat{p}=\frac{\vec{p}}{|\vec{p}|}=\frac{x, y, z}{\sqrt{x^2+y^2+z^2}}=\frac{(3,-12,4)}{13}=\left(\frac{3}{13}, \frac{-12}{13}, \frac{4}{13}\right)
\end{aligned}
\)
If written in unit vector component format then the formula is:
\(
\begin{aligned}
&\hat{p}=\frac{\vec{p}}{|\vec{p}|}=\frac{x \hat{i}+y \hat{j}+z \hat{k}}{\sqrt{x^2+y^2+z^2}}=\left(\frac{x}{\sqrt{x^2+y^2+z^2}} \hat{i}+\frac{y}{\sqrt{x^2+y^2+z^2}} \hat{j}+\frac{z}{\sqrt{x^2+y^2+z^2}} \hat{k}\right) \\
&\hat{p}=\frac{\vec{p}}{|\vec{p}|}=\frac{x \hat{i}+y \hat{j}+z \hat{k}}{\sqrt{x^2+y^2+z^2}}=\frac{3 \hat{i}-12 \hat{j}+\hat{4} i}{13}=\left(\frac{3}{13} \hat{i}+\frac{-12}{13} \hat{j}+\frac{4}{13} \hat{k}\right)
\end{aligned}
\)