We will discuss the equation of a line under different conditions. A line can be in different forms like horizontal, vertical, point-slope, two-point, etc.

Horizontal and vertical lines

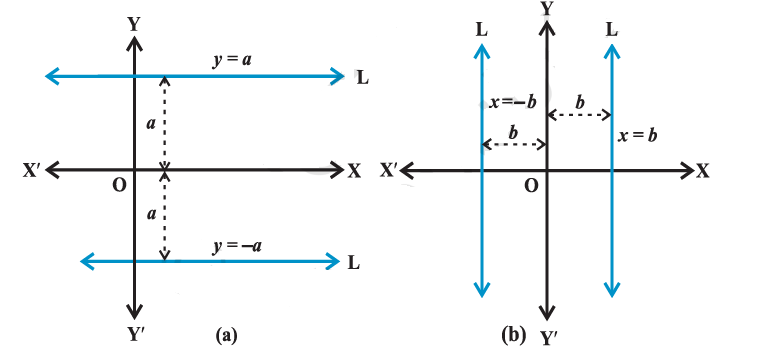
If a horizontal line \(\mathrm{L}\) is at distance \(a\) from the \(x\)-axis then ordinate of every point lying on the line is either \(a\) or \(-a\) [Fig (a)]. Therefore, equation of the line \(\mathrm{L}\) is either
\(y=a\) or \(y=-a\).
The choice of sign will depend upon the position of the line according as the line is above or below the \(y\)-axis.

Similarly, the equation of a vertical line at a distance \(b\) from the \(y\)-axis is either (Fig (b))

\(x=b\) or \(x=-b\)

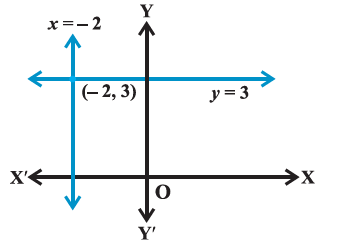
Example 1: Find the equation of the lines parallel to axes and passing through (-2,3).

Solution:

The position of the lines is shown in the figure above. The \(y\)-coordinate of every point on the line parallel to \(x\)-axis is 3, therefore, the equation of the line parallel to \(x\)-axis and passing through \((-2,3)\) is
\(y=3\).
Similarly, the equation of the line parallel to \(y\)-axis and passing through \((-2,3)\) is
\(x=-2\).

Point-slope form

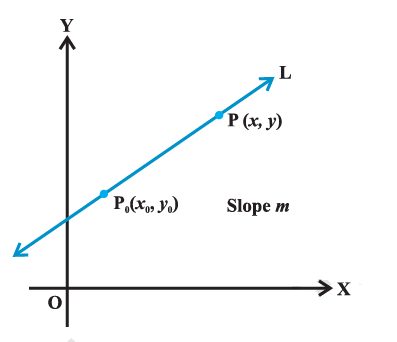
Suppose that \(\mathrm{P}_0\left(x_0, y_0\right)\) is a fixed point on a non-vertical line \(\mathrm{L}\), whose slope is \(m\).
Let \(\mathrm{P}(x, y)\) be an arbitrary point on L (Figure above). Then, by the definition, the slope of \(\mathrm{L}\) is given by
\(
m=\frac{y-y_0}{x-x_0} \text {, i.e., } y-y_0=m\left(x-x_0\right) \dots(1)
\)
Since the point \(\mathrm{P}_0\left(x_0, y_0\right)\) along with all points \((x, y)\) on L satisfies (1) and no other point in the plane satisfies (1). Equation (1) is indeed the equation for the given line L.
Thus, the point \((x, y)\) lies on the line with slope \(m\) through the fixed point \(\left(x_0, y_0\right)\), if and only if, its coordinates satisfy the equation
\(
y-y_0=m\left(x-x_0\right)
\)

Example 2: \(\text { Find the equation of the line through }(-2,3) \text { with slope }-4 \text {. }\)

Solution:

Here \(m=-4\) and given point \(\left(x_0, y_0\right)\) is \((-2,3)\).
By slope-intercept form formula
\(
y-y_0=m\left(x-x_0\right)
\)
Using this formula the equation of the given line is
\(
y-3=-4(x+2) \text { or }
\)
\(4 x+y+5=0\), which is the required equation.

Two-point form

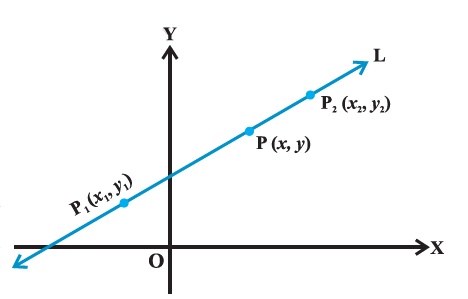
Let the line \(\mathrm{L}\) passes through two given points \(P_1\left(x_1, y_1\right)\) and \(P_2\left(x_2, y_2\right)\). Let \(\mathrm{P}(x, y)\) be a general point on L (Figure above).

The three points \(\mathrm{P}_1, \mathrm{P}_2\) and \(\mathrm{P}\) are collinear, therefore, we have slope of \(P_1 P=\) slope of \(P_1 P_2\)
\(
\text { i.e., } \quad \frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1}, \quad \text { or } y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right) \text {. }
\)
Thus, the equation of the line passing through the points \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) is given by
\(
y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right) \dots(2)
\)

Example 3: Write the equation of the line through the points (1, –1) and (3, 5).

Solution:

Here \(x_1=1, y_1=-1, x_2=3\) and \(y_2=5\). Using the two-point form (2) above for the equation of the line, we have
\(
y-(-1)=\frac{5-(-1)}{3-1}(x-1)
\)
or
\(-3 x+y+4=0\), which is the required equation.

Slope-intercept form

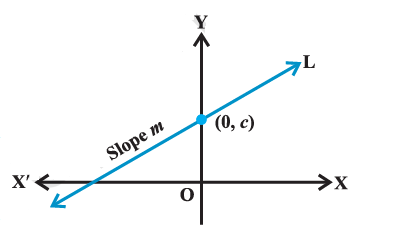
Sometimes a line is known to us with its slope and an intercept on one of the axes. We will now find equations of such lines.

Case I: Suppose a line L with slope \(m\) cuts the \(y\)-axis at a distance \(c\) from the origin (Figure above). The distance \(c\) is called the \(y\) intercept of the line L. Obviously, coordinates of the point where the line meet the \(y\)-axis are \((0, c)\). Thus, L has slope \(m\) and passes through a fixed point \((0, c)\). Therefore, by point-slope form, the equation of \(\mathrm{L}\) is
\(
y-c=m(x-0) \text { or } y=m x+c
\)
Thus, the point \((x, y)\) on the line with slope \(m\) and \(y\)-intercept \(c\) lies on the line if and
only if
\(
y=m x+c \dots(3)
\)
Note that the value of \(c\) will be positive or negative according as the intercept is made on the positive or negative side of the \(y\)-axis, respectively.

Case II: Suppose line L with slope \(m\) makes \(x\)-intercept \(d\). Then equation of \(\mathrm{L}\) is
\(
y-0=m(x-d)
\)
\(
y=m(x-d) \dots(4)
\)

Example 4: Write the equation of the lines for which \(\tan \theta=\frac{1}{2}\), where \(\theta\) is the inclination of the line and

(i) \(y\)-intercept is \(-\frac{3}{2}\)
(ii) \(x\)-intercept is 4.

Solution:

(i) Here, the slope of the line is \(m=\tan \theta=\frac{1}{2}\) and \(y\) – intercept \(c=-\frac{3}{2}\). Therefore, by slope-intercept form (3) above, the equation of the line is
\(
y=\frac{1}{2} x-\frac{3}{2} \text { or } 2 y-x+3=0,
\)
which is the required equation.

(ii) Here, we have \(m=\tan \theta=\frac{1}{2}\) and \(d=4\).
Therefore, by slope-intercept form (4) above, the equation of the line is
\(
y=\frac{1}{2}(x-4) \text { or } 2 y-x+4=0,
\)
which is the required equation.

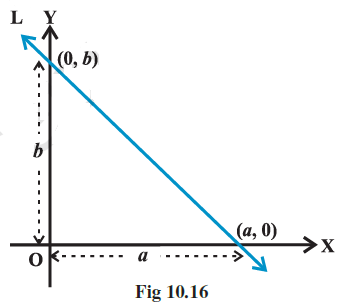
Intercept – form

Suppose a line L makes \(x\)-intercept \(a\) and \(y\)-intercept \(b\) on the axes. Obviously L meets \(x\)-ax is at the point \((a, 0)\) and \(y\)-axis at the point \((0, b)\) (Figure below). By two-point form of the equation of the line, we have

\(y-b=\frac{0-b}{a-0}(x-0) \quad\) or \(\quad a y=-b x+a b\),
i.e., \(\quad \frac{x}{a}+\frac{y}{b}=1\).
Thus, the equation of the line-making intercepts \(a\) and \(b\) on \(x\)-and \(y\)-axis, respectively, is
\(
\frac{x}{a}+\frac{y}{b}=1 \dots(5)
\)

Example 5: Find the equation of the line, which makes intercepts \(-3\) and 2 on the \(x\) – and \(y\)-axes respectively.

Solution:

Here \(a=-3\) and \(b=2\). By intercept form (5) above, the equation of the line is
\(
\frac{x}{-3}+\frac{y}{2}=1 \quad \text { or } \quad 2 x-3 y+6=0 .
\)

Normal form

Suppose a non-vertical line is known to us with the following data:
(i) Length of the perpendicular (normal) from the origin to the line.
(ii) Angle which normal makes with the positive direction of x-axis.

Let \(\mathrm{L}\) be the line, whose perpendicular distance from origin \(\mathrm{O}\) be \(\mathrm{OA}=p\) and the angle between the positive \(x\)-axis and \(\mathrm{OA}\) be \(\angle \mathrm{XOA}=\omega\). The possible positions of line \(\mathrm{L}\) in the Cartesian plane are shown in the Figure below. Now, our purpose is to find slope of \(\mathrm{L}\) and a point on it. Draw perpendicular AM on the \(x\)-axis in each case.

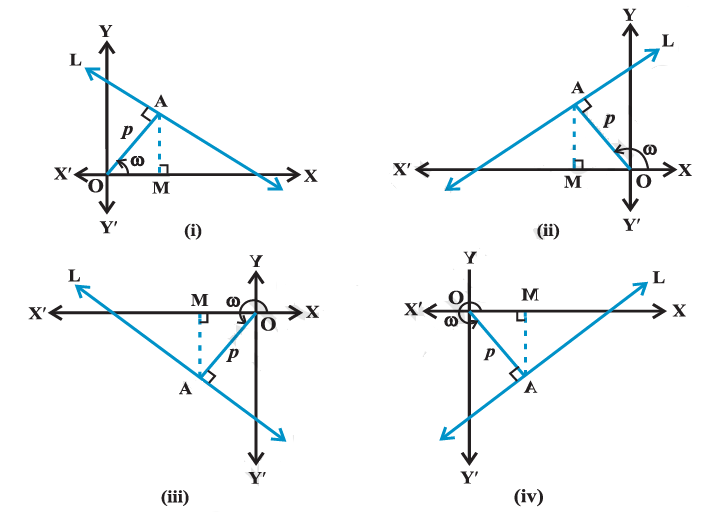
In each case, we have \(\mathrm{OM}=p \cos \omega\) and \(\mathrm{MA}=p \sin \omega\), so that the coordinates of the point \(\mathrm{A}\) are \((p \cos \omega, p \sin \omega)\).
Further, line \(\mathrm{L}\) is perpendicular to \(\mathrm{OA}\). Therefore
The slope of the line \(L=-\frac{1}{\text { slope of OA }}=-\frac{1}{\tan \omega}=-\frac{\cos \omega}{\sin \omega}\).
Thus, the line \(\mathrm{L}\) has slope \(-\frac{\cos \omega}{\sin \omega}\) and point \(\mathrm{A}(p \cos \omega, p \sin \omega)\) on it. Therefore, by point-slope form, the equation of the line \(\mathrm{L}\) is
\(
y-p \sin \omega=-\frac{\cos \omega}{\sin \omega}(x-p \cos \omega) \quad \text { or } \quad x \cos \omega+y \sin \omega=p\left(\sin ^2 \omega+\cos ^2 \omega\right)
\)
or \(\quad x \cos \omega+y \sin \omega=p\).
Hence, the equation of the line having normal distance \(p\) from the origin and angle \(\omega\) which the normal makes with the positive direction of \(x\)-axis is given by
\(
x \cos \omega+y \sin \omega=p \dots(6)
\)

Example 6: Find the equation of the line whose perpendicular distance from the origin is 4 units and the angle which the normal makes with the positive direction of \(x\)-axis is \(15^{\circ}\).

Solution:

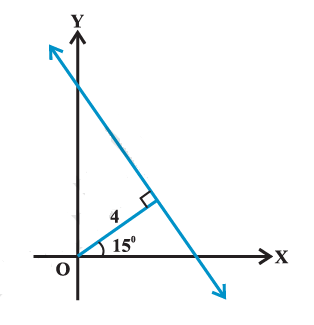
Here, we are given \(p=4\) and \(\omega=15^0(\) Figure above).
Now \(\quad \cos 15^{\circ}=\frac{\sqrt{3}+1}{2 \sqrt{2}}\)
and \(\quad \sin 15^{\circ}=\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
By the normal form (6) above, the equation of the line is
\(x \cos 15^0+y \sin 15^{\circ}=4\) or \(\frac{\sqrt{3}+1}{2 \sqrt{2}} x+\frac{\sqrt{3}-1}{2 \sqrt{2}} y=4\) or \((\sqrt{3}+1) x+(\sqrt{3}-1) y=8 \sqrt{2}\).
This is the required equation.