What is a Unit Circle?

A unit circle is a circle with a radius measuring 1 unit. The unit circle is generally represented in the cartesian coordinate plane. The unit circle is algebraically represented using the second-degree equation with two variables \(x\) and \(y\). The unit circle has applications in trigonometry and is helpful to find the values of the trigonometric ratios sine, cosine, and tangent.

Equation of a Unit Circle

The general equation of a circle is \((x-a)^2+(y-b)^2=r^2\), which represents a circle having the center \((a, b)\) and the radius \(r\). This equation of a circle is simplified to represent the equation of a unit circle. A unit circle is formed with its center at the point \((0,0)\), which is the origin of the coordinate axes. and a radius of 1 unit. Hence the equation of the unit circle is \((x-0)^2+(y-0)^2=1^2\). This is simplified to obtain the equation of a unit circle.

Equation of a Unit Circle: \(x^2+y^2=1\)

Here for the unit circle, the center lies at \((0,0)\) and the radius is 1 unit. The above equation satisfies all the points lying on the circle across the four quadrants.

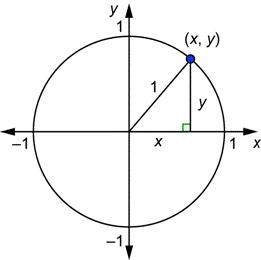
Finding Trigonometric Functions Using a Unit Circle

We can calculate the trigonometric functions of sine, cosine, and tangent using a unit circle. Let us apply the Pythagoras theorem in a unit circle to understand the trigonometric functions. Consider a right triangle placed in a unit circle in the cartesian coordinate plane. The radius of the circle represents the hypotenuse of the right triangle. The radius vector makes an angle \(\theta\) with the positive \(x\)-axis and the coordinates of the endpoint of the radius vector is \((x, y)\). Here the values of \(x\) and \(y\) are the lengths of the base and the altitude of the right triangle. Now we have a right-angle triangle with the sides 1, \(x, y\).

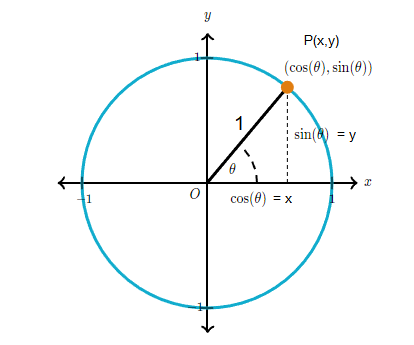
Applying this in trigonometry, we can find the values of the trigonometric ratio, as follows:

\(
\begin{array}{ll}
\sin \theta=\frac{\text { opposite }}{\text { hypotenuse }}=\frac{y}{1}=y & \csc \theta=\frac{\text { hypotenuse }}{\text { opposite }}=\frac{1}{y} \\
\cos \theta=\frac{\text { adjacent }}{\text { hypotenuse }}=\frac{x}{1}=x & \sec \theta=\frac{\text { hypotenuse }}{\text { adjacent }}=\frac{1}{x} \\
\tan \theta=\frac{\text { opposite }}{\text { adjacent }}=\frac{y}{x} & \cot \theta=\frac{\text { adjacent }}{\text { opposite }}=\frac{x}{y}
\end{array} 
\)

 

Note: Since we know \(\sin \theta=y, \cos \theta=x\), and using this we can obtain the values of the other trigonometric ratios using the right-angled triangle within the unit circle.

Example 1: Does the point \(P(1 / 2,1 / 2)\) lie on the unit circle?

Solution: We know that equation of a unit circle is:
\(x^2+y^2=1\)
Substituting \(x=1 / 2\) and \(y=1 / 2\), we get:
\(
\begin{aligned}
&=x^2+y^2 \\
&=(1 / 2)^2+(1 / 2)^2 \\
&=1 / 4+1 / 4 \\
&=1 / 2 \\
&\neq 1
\end{aligned}
\)
Since, \(x^2+y^2 \neq 1\), the point \(P(1 / 2,1 / 2)\) does not lie on the unit circle.

Unit Circle Chart in Radians

The unit circle represents a complete angle of \(2 \pi\) radians. And the unit circle is divided into four quadrants at angles of \(\pi / 2, \pi .3 \pi / 2\), and \(2 \pi\) respectively. Further within the first quadrant at the angles of \(0, \pi / 6\), \(\pi / 4, \pi / 3, \pi / 2\) are the standard values, which are applicable to the trigonometric ratios. The points on the unit circle for these angles represent the standard angle values of the cosine and sine ratios. On close observation of the below figure the values are repeated across the four quadrants, but with a change in sign. This change in sign is because of the reference \(x\)-axis and \(y\)-axis, which are positive on one side and negative on the other side of the origin. Now with the help of this, we can easily find the trigonometric ratio values of standard angles, across the four quadrants of the unit circle.

 

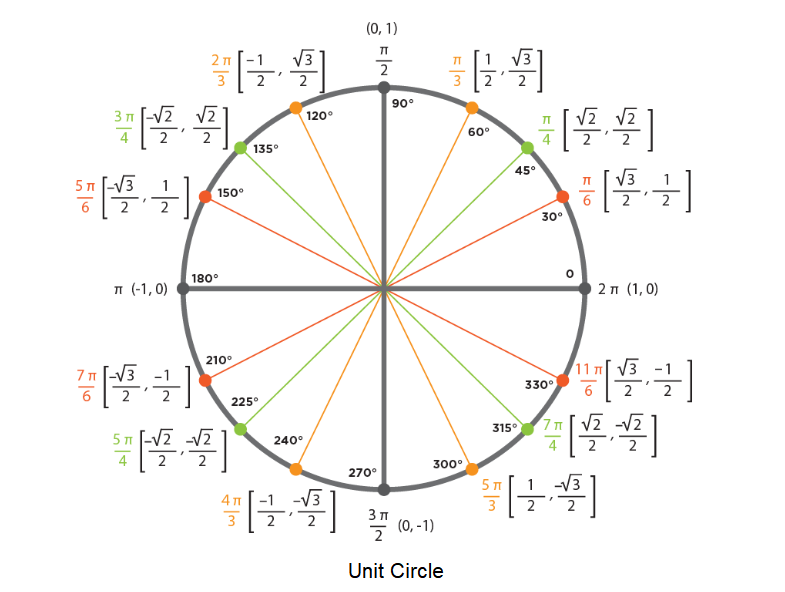
Example 2: Find the value of \(\sin 900^{\circ}\) using the unit circle chart.

Solution:

Since, the unit circle has \(0^{\circ}-360^{\circ}\), let us represent \(900^{\circ}\) in terms of \(360^{\circ}\).
\(900^{\circ}\) is 2 full rotations of \(360^{\circ}\) and an additional rotation of \(180^{\circ}\).
Hence, \(900^{\circ}\) will have the same trigonometric ratio as \(180^{\circ}\).
Therefore,
\(\sin 900^{\circ}=\sin 180^{\circ}\)
From the unit circle chart, we know that:
\(\sin 180^{\circ}=0\)