Trignometric Identities

\(
\begin{aligned}
& \sin ^2 \theta+\cos ^2 \theta=1 \\
& 1+\tan ^2 \theta=\sec ^2 \theta \\
& 1+\cot ^2 \theta=\cos ^2 \theta \\
& \sin ^4 \theta+\cos ^4=1-2 \sin ^2 \theta \cos ^2 \theta \\
& \sin ^6 \theta+\cos ^6=1-3 \sin ^2 \theta \cos ^2 \theta
\end{aligned}
\)

Remember:
\(
\sec \theta-\tan \theta=\frac{1}{\sec \theta+\tan \theta}
\)
and \(\operatorname{cosec} \theta-\cot \theta=\frac{1}{\operatorname{cosec} \theta+\cot \theta}\)

Trigonometry Formulas Involving Sum and Difference Identities

\(
\begin{aligned}
&\sin (x+y)=\sin (x) \cos (y)+\cos (x) \sin (y) \\
&\cos (x+y)=\cos (x) \cos (y)-\sin (x) \sin (y) \\
&\tan (x+y)=(\tan x+\tan y) /(1-\tan x \cdot \tan y) \\
&\sin (x-y)=\sin (x) \cos (y)-\cos (x) \sin (y) \\
&\cos (x-y)=\cos (x) \cos (y)+\sin (x) \sin (y) \\
&\tan (x-y)=(\tan x-\tan y) /(1+\tan x \cdot \tan y) \\
\end{aligned}
\)

Trigonometry Formulas Involving Half-Angle Identities

\(
\begin{aligned}
& \sin \left(\frac{x}{2}\right)= \pm \sqrt{\frac{1-\cos (x)}{2}} \\
& \cos \left(\frac{x}{2}\right)= \pm \sqrt{\frac{1+\cos (x)}{2}}
\end{aligned}
\)
\(
\begin{aligned}
\tan \left(\frac{x}{2}\right) & = \pm \sqrt{\frac{1-\cos (x)}{1+\cos (x)}} \\
& =\frac{1-\cos (x)}{\sin (x)} \\
& =\frac{\sin (x)}{1+\cos (x)}
\end{aligned}
\)

\(
\begin{aligned}
& \sin ^2(x)=\frac{1}{2}[1-\cos (2 x)] \\
& \cos ^2(x)=\frac{1}{2}[1+\cos (2 x)] \\
& \tan ^2(x)=\frac{1-\cos (2 x)}{1+\cos (2 x)}
\end{aligned}
\)

Trigonometry Formulas Involving Double Angle Identities

\(
\begin{aligned}
&\sin (2 x)=2 \sin (x) \cdot \cos (x)=\left[2 \tan x /\left(1+\tan ^2 x\right)\right]\\
&\cos (2 x)=\cos ^2(x)-\sin ^2(x)=\left[\left(1-\tan ^2 x\right) /\left(1+\tan ^2 x\right)\right]\\
&\cos (2 x)=2 \cos ^2(x)-1=1-2 \sin ^2(x)\\
&\tan (2 x)=[2 \tan (x)] /\left[1-\tan ^2(x)\right]\\
&\sec (2 x)=\sec ^2 x /\left(2-\sec ^2 x\right)\\
&\operatorname{cosec}(2 x)=(\sec x \cdot \operatorname{cosec} x) / 2
\end{aligned}
\)

Trigonometry Formulas Involving Triple Angle Identities

\(
\begin{aligned}
&\sin 3 x=3 \sin x-4 \sin ^3 x \\
&\cos 3 x=4 \cos ^3 x-3 \cos x \\
&\tan 3 x=\left[3 \tan x-\tan ^3 x\right] /\left[1-3 \tan ^2 x\right]
\end{aligned}
\)

Trigonometry Formulas Involving Product Identities

\(
\begin{aligned}
&\sin x \cdot \cos y=[\sin (x+y)+\sin (x-y)] / 2 \\
&\cos x \cdot \cos y=[\cos (x+y)+\cos (x-y)] / 2 \\
&\sin x \cdot \sin y=[\cos (x-y)-\cos (x+y)] / 2
\end{aligned}
\)

Trigonometry Formulas Involving Sum to Product Identities

\(
\begin{aligned}
&\sin x+\sin y=2[\sin ((x+y) / 2) \cos ((x-y) / 2)] \\
&\sin x-\sin y=2[\cos ((x+y) / 2) \sin ((x-y) / 2)] \\
&\cos x+\cos y=2[\cos ((x+y) / 2) \cos ((x-y) / 2)] \\
&\cos x-\cos y=-2[\sin ((x+y) / 2) \sin ((x-y) / 2)]
\end{aligned}
\)

Inverse Trigonometry Formulas

\(
\begin{aligned}
& \sin (-x)=-\sin (x) \\
& \cos (-x)=\cos (x) \\
& \tan (-x)=-\tan (x) \\
&\sin ^{-1}(-x)=-\sin ^{-1} x \\
&\cos ^{-1}(-x)=\pi-\cos ^{-1} x \\
&\tan ^{-1}(-x)=-\tan ^{-1} x \\
&\operatorname{cosec}^{-1}(-x)=-\operatorname{cosec}^{-1} x \\
&\sec ^{-1}(-x)=\pi-\sec ^{-1} x \\
&\cot ^{-1}(-x)=\pi-\cot ^{-1} x
\end{aligned}
\)

Maximum and Minimum Value of Standard Trigonometric Expressions

• Maximum value of \(a \cos \theta \pm b \sin \theta=\sqrt{a^2+b^2}\)
• Minimum value of \(a \cos \theta \pm b \sin \theta=-\sqrt{a^2+b^2}\)
• Maximum value of \(a \cos \theta \pm b \sin \theta+c=c+\sqrt{a^2+b^2}\)
• Minimum value of \(a \cos \theta \pm b \sin \theta+c=c-\sqrt{a^2+b^2}\)

Trigonometric Ratios of Compound Angles

The algebraic sum of two or more angles is generally called compound angles, and angles are known as constituent angles.

Some Important Results

• \(\sin (A \pm B)=\sin A \cos B \pm \cos A \sin B\)
• \(\cos (A \pm B)=\cos A \cos B \mp \sin A \sin B\)
• \(\tan (A \pm B)=\frac{\tan A+\tan B}{1 \tan A \tan B}\)
• \(\cot (A \pm B)=\frac{\cot A \cot B+1}{\cot B \pm \cot A}\)
• \(\sin (A+B) \sin (A-B)=\sin ^2 A-\sin ^2 B=\cos ^2 B-\cos ^2 A\)
• \(\cos (A+B) \cos (A-B)=\cos ^2 A-\sin ^2 B=\cos ^2 B-\sin ^2 A\)
• \(\sin (A+B+C)=\sin A \cos B \cos C+\sin B \cos A \cos C+\sin C \cos A \cos B-\sin A \sin B \sin C\)
• \(\cos (A+B+C)=\cos A \cos B \cos C-\cos A \sin B \sin C-\cos B \sin A \sin C-\cos C \sin A \sin B\)
• \(\tan (A+B+C)=\frac{\tan A+\tan B+\tan C-\tan A \tan B \tan C}{1-\tan A \tan B-\tan B \tan C-\tan C \tan A}\)

T-Ratio of Multiple Angles

• \(\sin 2 A=2 \sin A \cos A=\frac{2 \tan A}{1+\tan ^2 A}\)
• \(\cos 2 A=2 \cos ^2 A-1=1-2 \sin ^2 A=\frac{1-\tan ^2 A}{1+\tan ^2 A}=\cos ^2 A-\sin ^2 A\)
• \(\tan 2 A=\frac{2 \tan A}{1-\tan ^2 A}\)
• \(\sin 3 A=3 \sin A-4 \sin ^3 A\)
• \(\cos 3 A=4 \cos ^3 A-3 \cos A\)
• \(\tan 3 A=\frac{3 \tan A-\tan ^3 A}{1-3 \tan ^2 A}\)

Remember
\(
\begin{aligned}
& 1+\cos 2 A=2 \cos ^2 A \\
& 1-\cos 2 A=2 \sin ^2 A \\
& \frac{1-\cos 2 A}{1+\cos 2 A}=\tan ^2 A
\end{aligned}
\)

Values of T-Ratios at Some Useful Angles

• \(\sin 75^{\circ}=\frac{\sqrt{3}+1}{2 \sqrt{2}}=\cos 15^{\circ}\)
• \(\cos 75^{\circ}=\frac{\sqrt{3}-1}{2 \sqrt{2}}=\sin 15^{\circ}\)
• \(\tan 75^{\circ}=2+\sqrt{3}=\cot 15^{\circ}\)
• \(\cot 75^{\circ}=2-\sqrt{3}=\tan 15^{\circ}\)
• \(\sin 9^{\circ}=\frac{\sqrt{3+\sqrt{5}}-\sqrt{5-\sqrt{5}}}{4}=\cos 81^{\circ}\)
• \(\cos 9^{\circ}=\frac{\sqrt{3+\sqrt{5}}-\sqrt{5-\sqrt{5}}}{4}=\sin 81^{\circ}\)

Important Results

\(
\begin{aligned}
& \sin \theta \sin (60-\theta) \sin (60+\theta)=\frac{1}{4} \sin 3 \theta \\
& \cos \theta \cos (60-\theta) \cos (60+\theta)=\frac{1}{4} \cos 3 \theta \\
& \tan \theta \tan (60-\theta) \tan (60+\theta)=\tan 3 \theta
\end{aligned}
\)

Summation of Series in Trigonometry

• \(\sin \alpha+\sin (\alpha+\beta)+\sin (\alpha+2 \beta)+\ldots \ldots \ldots+\sin (\alpha+(n-1) \beta)=\frac{\sin \left[\alpha+\frac{(n-1)}{2} \beta\right] \sin \frac{n \beta}{2}}{\sin \frac{\beta}{2}}\). When the angles of sine are in AP, the sum of the sine series is given by this formula.
• However, if \(\alpha=\beta\) in the above case, Then
  
  \(\sin \alpha+\sin 2 \alpha+\sin 3 \alpha+\ldots \ldots \ldots+\sin \alpha=\frac{\sin \left(\frac{n+1}{2}\right) \alpha \sin \frac{n \alpha}{2}}{\sin \frac{\alpha}{2}}\)
• When cosine angles are in AP, \(\cos \alpha+\cos 2 \alpha+\cos \alpha+\ldots \ldots \ldots . \cos n \alpha=\frac{\cos \left(\frac{n+1}{2}\right) \alpha \sin \frac{n \alpha}{2}}{\sin \frac{\alpha}{2}}\)

Remember

If \(A , B\) and C are angles of \(\Delta\),

• \(\sin (B+C)=\sin A\)
• \(\cos (B+C)=-\cos A\)
• \(\sin \left(\frac{B+C}{2}\right)=\cos \frac{A}{2}\)
• \(\cos \left(\frac{B+C}{2}\right)=\sin \frac{A}{2}\)
• \(\sin 2 A+\sin 2 B+\sin 2 C=4 \sin A \sin B \sin C\)
• \(\cos 2 A+\cos 2 B+\cos 2 C=1-4 \cos A \cos B \cos C\)
• \(\tan A+\tan B+\tan C=\tan A \tan B \tan C\)

Trigonometric Equations

A solution of a trigonometric equation is the value of the unknown angle that satisfies the equation.

Following are general solutions of trigonometric equations in the standard form:
\(
\begin{array}{|c|c|}
\hline \text { Equation } & \text { General Solution } \\
\hline \sin \theta=0 & \theta=n \pi n \in z \\
\hline \cos \theta=0 & \theta=(2 n+1) \frac{\pi}{2} n \in z \\
\hline \tan \theta=0 & \theta=n \pi, n \in z \\
\hline \sin \theta=\sin \alpha & \theta=n \pi+(-1)^n \alpha, n \in z \\
\hline \cos \theta=\cos \alpha & \theta=2 n \pi \pm \alpha, n \in z \\
\hline \tan \theta=\tan \alpha & \theta=n \pi+\alpha, n \in z \\
\hline
\end{array}
\)

\(
\left.\begin{array}{rl}
\sin ^2 \theta & =\sin ^2 \alpha \\
\cos ^2 \theta & =\cos ^2 \alpha \\
\tan ^2 \theta & =\tan ^2 \alpha
\end{array}\right\} \quad \theta=n \pi \pm \alpha, n \in z
\)

Sine Rule

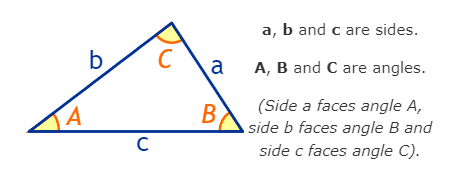
The Law of Sines (or Sine Rule) is very useful for solving triangles:

\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)

And it says that: When we divide side a by the sine of angle A, it is equal to side b divided by the sine of angle B, and also equal to side c divided by the sine of angle C.

Example 1: Calculate side “c” in the triangle given below.

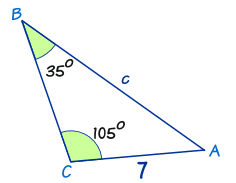
Solution:

Law of Sines: \(a / \sin A=b / \sin B=c / \sin C\)
Put in the values we know: \(a / \sin A=7 / \sin \left(35^{\circ}\right)=c / \sin \left(105^{\circ}\right)\)
Ignore \(a / \sin A\) (not useful to us): \(7 / \sin \left(35^{\circ}\right)=c / \sin \left(105^{\circ}\right)\)
Now we use our algebra skills to rearrange and solve:
Swap sides: \(c / \sin \left(105^{\circ}\right)=7 / \sin \left(35^{\circ}\right)\)
Multiply both sides by \(\sin \left(105^{\circ}\right): \quad c=\left(7 / \sin \left(35^{\circ}\right)\right) \times \sin \left(105^{\circ}\right)\)
Calculate: \(\mathrm{c}=(7 / 0.574 \ldots) \times 0.966 \ldots\)
\(\mathrm{c}=\mathbf{1 1 . 8}\)

Example 2: Calculate the missing lengths of the following triangle.

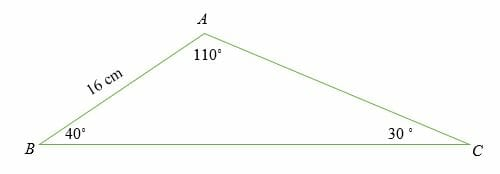
Solution:

\(a / \sin (A)=b / \sin (B)=c / \sin (C)\)
By substitution, we have,
a \(/\) sin \(110^{\circ}=16 /\) sin \(30^{\circ}\)
\(a=\left(16\right.\) sin \(\left.110^{\circ}\right) /\) sin \(30^{\circ}\)
\(a=30.1\)

Solving for b.
\(\mathrm{b} / \sin 40^{\circ}=16 / \sin 30^{\circ}\)
\(b=\left(16\right.\) sin \(\left.40^{\circ}\right) / \sin 30^{\circ}\)
\(
=20.6
\)
Therefore, length \(B C=30.1 \mathrm{~cm}\) and length \(A C=20.6 \mathrm{~cm}\).

Cosine Rule

The Law of Cosines (also called the Cosine Rule) says: \(c^2=a^2+b^2-2 a b \cos (C)\). It can be in either of these forms shown below.

\(
\begin{aligned}
&\cos (C)=\frac{a^2+b^2-c^2}{2 a b} \\
&\cos (A)=\frac{b^2+c^2-a^2}{2 b c} \\
&\cos (B)=\frac{c^2+a^2-b^2}{2 c a}
\end{aligned}
\)

Example 3: Find the angle B as shown in the figure below.

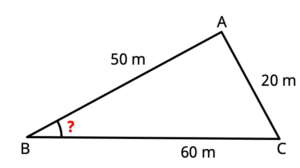
Solution:

By Law of Cosines,
\(
b^2=a^2+b^2-2 a b \cos B
\)
Putting values
\(
\begin{array}{ll}
20^2=60^2+50^2-2 \times 60 \times 50 \times \cos B \\
400=3600+2500-6000 \cos B \\
6000 \cos B=6100-400 \\
6000 \cos B=5700 \\
B=18.19^{\circ}
\end{array}
\)