Subtraction of a Vectors

Let \(\vec{a}\) and \(\vec{b}\) be two vectors. We define \(\vec{a}-\vec{b}\) as the sum of the vector \(\vec{a}\) and the vector \((-\vec{b})\). To subtract \(\vec{b}\) from \(\vec{a}\), invert the direction of \(\vec{b}\) and add to \(\vec{a}\). The figure below shows the process.

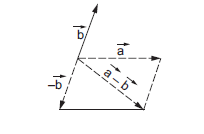
Vector Subtraction by Parallelogram Law

Using the parallelogram law of vector addition, we can determine the vector as follows. We interpret \(\vec{a}-\vec{b}\) as \(\vec{a}+(-\vec{b})\), that is, the vector sum of \(\vec{a}\) and \(-\vec{b}\). Now, we reverse vector \(\vec{b}\), and then add \(\vec{a}\) and – \(\vec{b}\) using the parallelogram law:

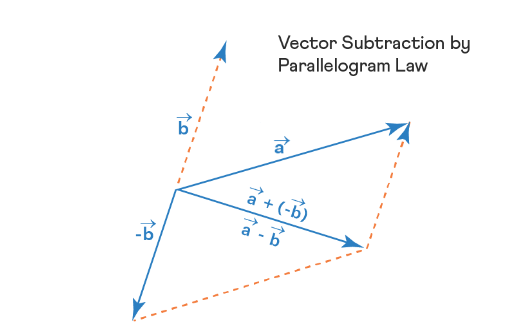
Vector Subtraction by Triangle Law

Now, we will interpret the subtraction of vectors using the triangle law of vector addition. Denote the vector drawn from the end-point of \(\vec{b}\) to the end-point of \(\vec{a}\) by \(\vec{c}\).

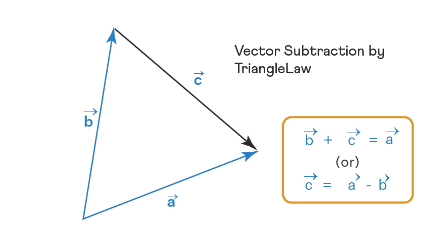
Subtraction of Two Vectors

Vector \(A – B\) can be written as \(A +(- B )\) or \(A – B\) is the vector addition of \(A\) and \(– B\). Suppose angle between two vectors \(A\) and \(B\) is \(\theta\). Then, angle between \(A\) and \(– B\) will be \(180^{\circ}-\theta\) as shown in Fig. (b)

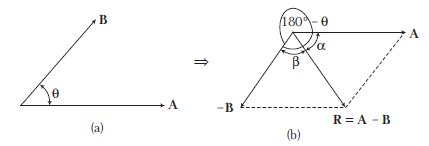
Magnitude of resultant vector \(R = A – B\) will be thus given by
\(
\begin{aligned}
& | R |=| A – B |=\sqrt{A^2+B^2+2 A B \cos \left(180^{\circ}-\theta\right)} \\
& \text { or } \quad| R |=\sqrt{A^2+B^2-2 A B \cos \theta} \dots(i) \\
&
\end{aligned}
\)
For direction of resultant vector \(R\), we will either calculate angle \(\alpha\) or \(\beta\), where
\(
\begin{aligned}
\tan \alpha & =\frac{B \sin \left(180^{\circ}-\theta\right)}{A+B \cos \left(180^{\circ}-\theta\right)}=\frac{B \sin \theta}{A-B \cos \theta} \dots(ii) \\
\text { or } \quad \tan \beta & =\frac{A \sin \left(180^{\circ}-\theta\right)}{B+A \cos \left(180^{\circ}-\theta\right)}=\frac{A \sin \theta}{B-A \cos \theta} \dots(iii)
\end{aligned}
\)

Remarks

• If two vectors have equal magnitudes, i.e. \(| A |=| B |=a\) and \(\theta\) is the angle between them, then
  \(
  | A – B |=\sqrt{a^2+a^2-2 a^2 \cos \theta}=2 a \sin \left(\frac{\theta}{2}\right)
  \)
• If \(\theta=60^{\circ}\), then \(2 a \sin \left(\frac{\theta}{2}\right)=a\)
  i.e. \(| A – B |=| A |=| B |=a\) at \(\theta=60^{\circ}\)
• If two vectors are such that their sum and difference have equal magnitude, then angle between the given vectors \(\theta=90^{\circ}\).
  i.e. \(| A + B |=| A – B |\)
  then \(\cos \theta=0\) or \(\theta=90^{\circ}\)
• If \(A + B = A – B\)
  then \(B = 0\) (a null vector)
• The vector subtraction does not follow commutative law, i.e. \(A – B \neq B – A\).
• The vector subtraction does not follow associative law, i.e. \(A-(B-C) \neq(A-B)-C\)

Example 1: Two vectors of equal magnitude 5 unit have an angle \(60^{\circ}\) between them. Find the magnitude of \((a)\) the sum of the vectors and (b) the difference of the vectors.

Solution:

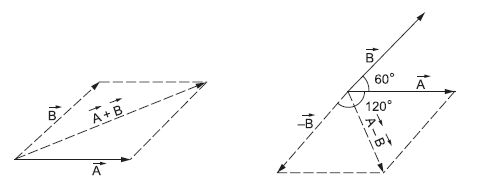
The figure above shows the construction of the sum \(\vec{A}+\vec{B}\) and the difference \(\vec{A}-\vec{B}\)

(a) \(\vec{A}+\vec{B}\) is the sum of \(\vec{A}\) and \(\vec{B}\). Both have a magnitude of 5 unit and the angle between them is \(60^{\circ}\). Thus, the magnitude of the sum is
\(
\begin{aligned}
|\vec{A}+\vec{B}| &=\sqrt{5^2+5^2+2 \times 5 \times 5 \text { cos } 60^{\circ}} \\
&=5 \sqrt{3} \text { unit. }
\end{aligned}
\)

(b) \(\vec{A}-\vec{B}\) is the sum of \(\vec{A}\) and \((-\vec{B})\). As shown in the figure, the angle between \(\vec{A}\) and \((-\vec{B})\) is \(120^{\circ}\). The magnitudes of both \(\vec{A}\) and \((-\vec{B})\) is 5 unit. So,
\(
\begin{aligned}
|\vec{A}-\vec{B}| &=\sqrt{5^2+5^2+2 \times 5 \times 5 \cos 120^{\circ}} \\
&=5 \text { unit }
\end{aligned}
\)

Example 2: Obtain the magnitude of \(2 A -3 B\), if \(A =\hat{ i }+\hat{ j }-2 \hat{ k }\) and \(B =2 \hat{ i }-\hat{ j }+\hat{ k }\).

Solution: The magnitude of \(2 A -3 B\) is
\(
\begin{aligned}
2 A -3 B & =2(\hat{ i }+\hat{ j }-2 \hat{ k })-3(2 \hat{ i }-\hat{ j }+\hat{ k }) \\
& =-4 \hat{ i }+5 \hat{ j }-7 \hat{ k }
\end{aligned}
\)
\(
\begin{aligned}
\therefore \text { Magnitude of } 2 A -3 B & =\sqrt{(-4)^2+(5)^2+(-7)^2} \\
& =\sqrt{16+25+49} \\
& =\sqrt{90}
\end{aligned}
\)