Slope of a Line
The slope of a line determines how steep the line is. The slope is represented by \({m}\). which tells us how much the \(y\)-value changes as the \(x\)-value changes.
\(
\text { slope }=m=\frac{\text { rise }}{\text { run }}=\frac{\text { change in } y}{\text { change in } x}=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}
\)
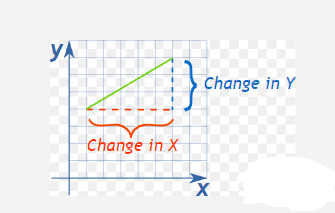
We can also define the slope as shown in figure below.
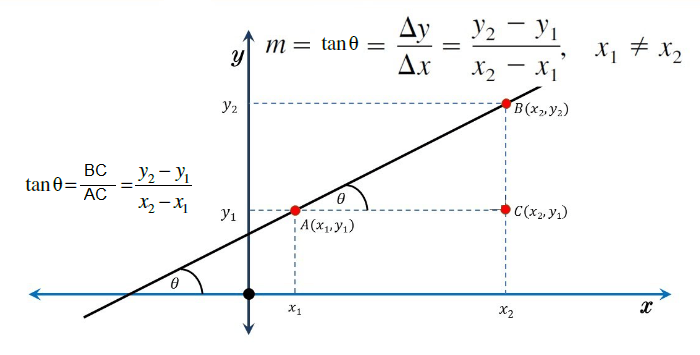
Equation of a Straight Line
The equation of a straight line is usually written as \(y=m x+c\).
Where, \({y}=\) how far up
\({x}=\) how far along
\({m}=\) Slope or Gradient (how steep the line is)
\({c}=\) value of \({y}\) when \({x}={0}\)
In the figure below you can see, the \({c}=1\), and the slope \(m=(3-1)/(1-0)=2\)
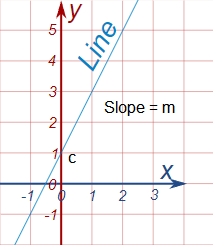
Therefore the equation of the above straight line is \(y=2 x+1\)
Positive and negative slope
If the slope of a line is positive, the line increases (goes up) as it moves from left to right. If the slope of a line is negative, the line decreases (goes down) as it moves from left to right. Below are four lines where the only difference is that one slope is positive, the other is negative, a line with zero slope, and a line with an undefined slope.
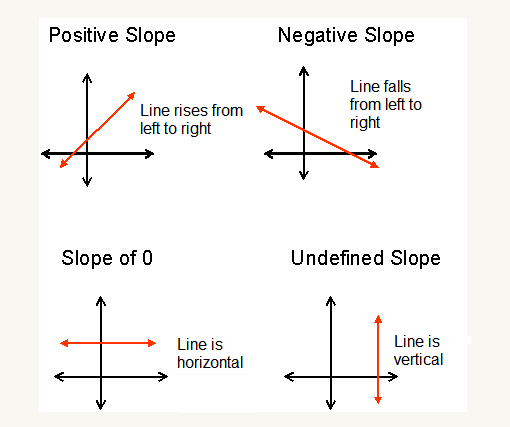
When the slope is 0, the line is a horizontal line that passes through the \(y\)-intercept. The slope of a vertical line is undefined since there is 0 horizontal change, so
\(
\text { slope }=m=\frac{\text { change in } y}{0}=\text { undefined }
\)
Finding the slope from a graph
Given the graph of any line, it is possible to find the slope of the line by choosing two points on the line( Assume Point P and Point Q). The simplest way to do this is to pick 2 points on the line at integer coordinates and then count the change in x and the change in y.
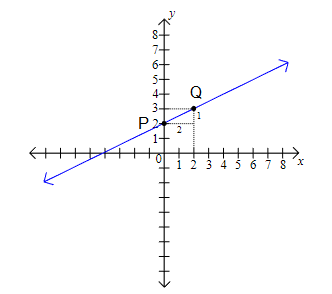
In the graph above, we can see that for every 2 units change in \(x\), there is a 1 unit change in \(y\), so the slope of the line is \(m=\frac{(3-2)}{(2-0)}=\frac{1}{2}\). It also intersects the \(y\)-axis at the point P \((0,2)\), so the \(y\)-intercept is 2 . Since we know both the slope and the y-intercept, we can find the equation of the graph:
\(
y=\frac{1}{2} x+2
\)
Example 1: Find the slope of the line passing through the points (3, – 2) and (–1, 4).
Solution:
\(m=\frac{y_2-y_1}{x_2-x_1}
\)
The slope of the line through \((3,-2)\) and \((-1,4)\) is
\(
m=\frac{4-(-2)}{-1-3}=\frac{6}{-4}=-\frac{3}{2} .
\)
Example 2: Find the slope of the line passing through the points (3, – 2) and (7, – 2).
Solution:
\(m=\frac{y_2-y_1}{x_2-x_1}=\frac{-2-(-2)}{7-3}=\frac{0}{4}=0
\)
Example 3: Find the slope of the graph shown below.
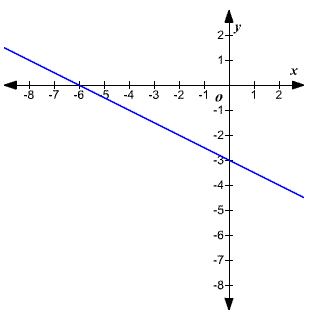
Solution:
Here the line crosses the \(y\)-axis at \(-3\), so the \(y\)-intercept is \(-3\).
To find the slope, use the two points \((-6,0)\) and \((0,-3)\) and substitute these in the slope formula:
\(
\begin{aligned}
m & =\frac{y_2-y_1}{x_2-x_1} \\
& =\frac{-3-0}{0-(-6)} \\
& =-\frac{1}{2}
\end{aligned}
\)
So, the equation of the graph: \(y=-\frac{1}{2} x-3\)
Example 4: Find the equation of the line given in the graph as shown below.
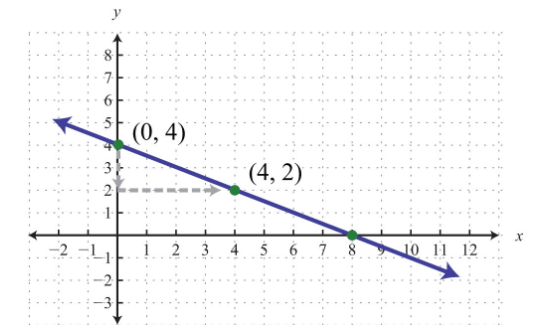
Solution:
From the graph, we can see that the \(y\)-intercept is \((0,4)\), and thus
\(
c=4
\)
Furthermore, from the points \((0,4)\) to \((4,2)\), we can see that the rise is \(-2\) units and the run is 4 units.
\(
m=\frac{\Delta y}{\Delta x}=\frac{\text { rise }}{\text { run }}=\frac{-2}{4}=-\frac{1}{2}
\)
Now substitute \(m\) and \(c\) into slope-intercept form:
\(
\begin{aligned}
& y=m x+c \\
& y=-\frac{1}{2} x+4
\end{aligned}
\)
Example 5: \(\text { Find the equation of the line with slope } m=-\frac{2}{3} \text { passing through }(-6,3) \text {. }\)
Solution:
\(\begin{aligned}
& y=m x+c \\
& y=-\frac{2}{3} x+c
\end{aligned}
\)
For the ordered pair \((-6,3)\) to be a solution, it must solve the equation. Therefore, we can use it to find \(c\). Substitute the appropriate \(x\) – and \(y\)-values as follows:
\(
\begin{aligned}
& y=-\frac{2}{3} x+c \\
& (3)=-\frac{2}{3}(-6)+c
\end{aligned}
\)
After substituting the appropriate values, solve for the only remaining variable, \(c\).
\(
\begin{aligned}
3 & =-\frac{2}{3}(-6)+c \\
3 & =-2(-2)+c \\
3 & =4+b \\
-1 & =c
\end{aligned}
\)
Once we have \(c\), we can then complete the equation:
\(
\begin{aligned}
& y=m x+c \\
& y=-\frac{2}{3} x-1
\end{aligned}
\)
How to verify your equation is right?
As a check, verify that \((-6,3)\) solves this linear equation as follows:
\(
\begin{aligned}
& y=-\frac{2}{3} x-1 \\
& 3=-\frac{2}{3}(-6)-1 \\
& 3=-2 \cdot(-2)-1 \\
& 3=4-1 \\
& 3=3
\end{aligned}
\)
Example 6: Find the equation of the line passing through (−4, −2) and (1, 3).
Solution:
When finding a linear equation using slope-intercept form \(y=m x+c\), the goal is to find \(m\) and then \(c\).
Step 1: Find the slope \(m\). In this case, given two points, use the slope formula.
\(
\begin{aligned}
m & =\frac{y_2-y_1}{x_2-x_1} \\
& =\frac{3-(-2)}{1-(-4)} \\
& =\frac{3+2}{1+4} \\
& =\frac{5}{5} \\
& =1
\end{aligned}
\)
Substitute \(m=1\) into slope-intercept form.
\(
\begin{aligned}
& y=m x+c \\
& y=1 x+c
\end{aligned}
\)
Step 2: Find \(c\). To do this, substitute the coordinates of any given ordered pair solution. Use \((1,3)\) :
\(
\begin{aligned}
& y=1 x+c \\
& 3=1(1)+c \\
& 3=1+c \\
& 2=c
\end{aligned}
\)
Step 3: Finish building the equation by substituting in the value for \(c\). In this case, we use \(c=2\).
\(
\begin{aligned}
& y=1 x+c \\
& y=1 x+2
\end{aligned}
\)
\(
y=x+2
\)
Example 7: \(\text { Find the equation of the line passing through }(-5,3) \text { with slope } m=-\frac{2}{5} \text {. }\) Also draw the graph from the equation.
Solution:
Substitute \((-5,3)\) and \(m=-\frac{2}{5}\) into point-slope form.
\(
\begin{aligned}
y-y_1 & =m\left(x-x_1\right) \\
y-(3) & =-\frac{2}{5}(x-(-5)) \quad \text { Solve for } y \\
y-3 & =-\frac{2}{5}(x+5) \\
y-3 & =-\frac{2}{5} x-2 \\
y-3+3 & =-\frac{2}{5} x-2+3 \\
y & =-\frac{2}{5} x+1
\end{aligned}
\)
To draw the graph we have to find two points of the graph. We can substitute \(x\)=0 in the above equation, we get \(y\) = 1. Similarly, we put \(y\)=0 and find \(x\) = 5/2 = 2.5. Then join these two points using a straight line as shown below.
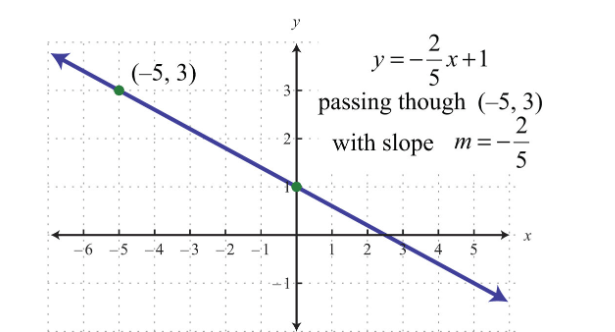
Example 8: Find the slope of the line-making inclination of \(60^{\circ}\) with the positive direction of \(x\)-axis.
Solution:
Here inclination of the line \(\theta=60^{\circ}\). Therefore, the slope of the line is
\(
m=\tan 60^{\circ}=\sqrt{3} \text {. }
\)
Example 9: \(\text { Graph } 3 x-2 y=-6\)
Solution:
The equation \(3 x-2 y=-6\) is written in the general form. To graph this equation with a table of values, first, solve the equation for \(y\) to write it in the form \(y=m x+c\), as shown:
\(
\begin{aligned}
3 x-2 y & =-6 \\
3 x-2 y-3 x & =-3 x-6 \\
-2 y & =-3 x-6 \\
\frac{-2 y}{-2} & =\frac{-3 x}{-2}-\frac{6}{-2} \\
y & =\frac{3}{2} x+3
\end{aligned}
\)
Next, choose three values for x and calculate the corresponding y-coordinates. (Hint: to cancel fractions, choose multiples of the denominator.) Plot the points in the table and draw a line through them.
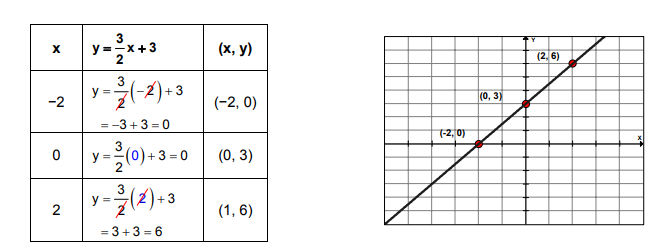
Example 10: \(\text { Graph }-2 x+4 y=8\)
Solution:
\(
\text { To graph the equation, find the } \mathrm{x} \text { – and } y \text {-intercepts. }
\)
To find the \({x}\)-intercept, let \({y}=\mathbf{0}\) and solve the equation for \(x\).
\(
\begin{array}{cl}
y=0, & -2 x+4 y=8 \\
& -2 x+4(0)=8 \\
& -2 x=8 \\
& x=-4
\end{array}
\)
The \(x\)-intercept is \((-4,0)\).
To find the \({y}\)-intercept, let \({x}={0}\) and solve the equation for \({y}\).
\(
\begin{array}{cc}
x=0, & -2 x+4 y=8 \\
-2(0)+4 y=8 \\
4 y=8 \\
y=2
\end{array}
\)
The \(y\)-intercept is \((0,2)\).
Next plot each intercept, label the points and draw a line through them.
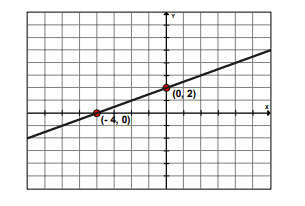
Conditions for parallelism and perpendicularity of lines in terms of their slopes
Parallel Lines:
In a coordinate plane, suppose that non-vertical lines \(l_1\) and \(l_2\) have slopes \(m_1\) and \(m_2\), respectively. Let their inclinations be \(\alpha\) and \(\beta\), respectively.
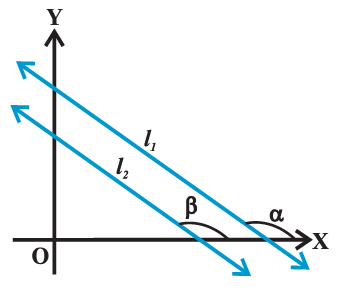
If the line \(l_1\) is parallel to \(l_2\) (as shown in the above figure) then their inclinations are equal, i.e.,
\(
\alpha=\beta \text {, and hence, } \tan \alpha=\tan \beta
\)
Therefore \(m_1=m_2\), i.e., their slopes are equal. Conversely, if the slope of two lines \(l_1\) and \(l_2\) is same, i.e.,
\(
m_1=m_2
\)
Then
\(\tan \alpha=\tan \beta\).
By the property of tangent function (between \(0^{\circ}\) and \(180^{\circ}\) ), \(\alpha=\beta\). Therefore, the lines are parallel.
Note: Hence, two non-vertical lines \(l_1\) and \(l_2\) are parallel if and only if their slopes are equal.
Perpendicular Lines:
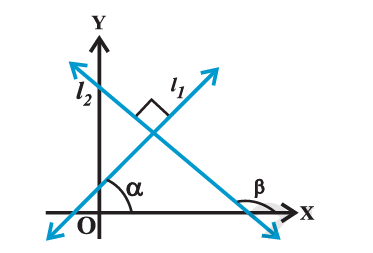
If the lines \(l_1\) and \(l_2\) are perpendicular (Fig above), then \(\beta=\alpha+90^{\circ}\). Therefore, \(\tan \beta=\tan \left(\alpha+90^{\circ}\right)\)
\(
=-\cot \alpha=-\frac{1}{\tan \alpha}
\)
i.e., \(\quad m_2=-\frac{1}{m_1} \quad\) or \(\quad m_1 m_2=-1\)
Conversely, if \(m_1 m_2=-1\), i.e., \(\tan \alpha \tan \beta=-1\).
Then \(\tan \alpha=-\cot \beta=\tan \left(\beta+90^{\circ}\right)\) or \(\tan \left(\beta-90^{\circ}\right)\)
Therefore, \(\alpha\) and \(\beta\) differ by \(90^{\circ}\).
Thus, lines \(l_1\) and \(l_2\) are perpendicular to each other.
Hence, two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other,
i.e., \(\quad m_2=-\frac{1}{m_1}\) or, \(m_1 m_2=-1\).
Example 11: Line through the points \((-2,6)\) and \((4,8)\) is perpendicular to the line through the points \((8,12)\) and \((x, 24)\). Find the value of \(x\).
Solution:
Slope of the line through the points \((-2,6)\) and \((4,8)\) is
\(
m_1=\frac{8-6}{4-(-2)}=\frac{2}{6}=\frac{1}{3}
\)
Slope of the line through the points \((8,12)\) and \((x, 24)\) is
\(
m_2=\frac{24-12}{x-8}=\frac{12}{x-8}
\)
Since two lines are perpendicular, \(m_1 m_2=-1\), which gives
\(
\frac{1}{3} \times \frac{12}{x-8}=-1 \text { or } x=4
\)
Angle between two lines
When we think about more than one line in a plane, then we find that these lines are either intersecting or parallel. Here we will discuss the angle between two lines in terms of their slopes.
Let \(\mathrm{L}_1\) and \(\mathrm{L}_2\) be two non-vertical lines with slopes \(m_1\) and \(m_2\), respectively. If \(\alpha_1\) and \(\alpha_2\) are the inclinations of lines \(L_1\) and \(L_2\), respectively. Then
\(
m_1=\tan \alpha_1 \text { and } m_2=\tan \alpha_2 .
\)
We know that when two lines intersect each other, they make two pairs of vertically opposite angles such that sum of any two adjacent angles is \(180^{\circ}\). Let \(\theta\) and \(\phi\) be the adjacent angles between the lines \(\mathrm{L}_1\) and \(\mathrm{L}_2\) (shown in figure below). Then \(\theta=\alpha_2-\alpha_1\) and \(\alpha_1, \alpha_2 \neq 90^{\circ}\).
Therefore \(\tan \theta=\tan \left(\alpha_2-\alpha_1\right)=\frac{\tan \alpha_2-\tan \alpha_1}{1+\tan \alpha_1 \tan \alpha_2}=\frac{m_2-m_1}{1+m_1 m_2} \quad\left(\right.\) as \(\left.1+m_1 m_2 \neq 0\right)\) and \(\phi=180^{\circ}-\theta\) so that
\(
\tan \phi=\tan \left(180^{\circ}-\theta\right)=-\tan \theta=-\frac{m_2-m_1}{1+m_1 m_2} \text {, as } 1+m_1 m_2 \neq 0
\)
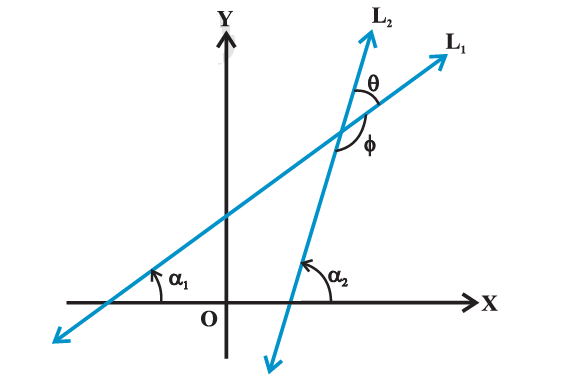
Now, there arise two cases:
Case I: If \(\frac{m_2-m_1}{1+m_1 m_2}\) is positive, then \(\tan \theta\) will be positive and \(\tan \phi\) will be negative, which means \(\theta\) will be acute and \(\phi\) will be obtuse.
Case II: If \(\frac{m_2-m_1}{1+m_1 m_2}\) is negative, then \(\tan \theta\) will be negative and \(\tan \phi\) will be positive, which means that \(\theta\) will be obtuse and \(\phi\) will be acute.
Thus, the acute angle (say \(\theta\) ) between lines \(\mathrm{L}_1\) and \(\mathrm{L}_2\) with slopes \(m_1\) and \(m_2\), respectively, is given by
\(
\tan \theta=\left|\frac{m_2-m_1}{1+m_1 m_2}\right| \text {, as } 1+m_1 m_2 \neq 0 \dots(1)
\)
The obtuse angle (say \(\phi\) ) can be found by using \(\phi=180^{\circ}-\theta\).
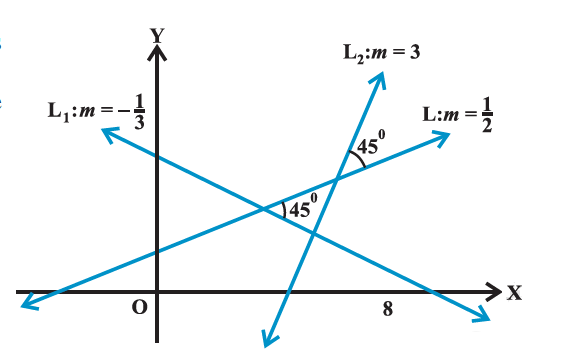
Example 12: If the angle between two lines is \(\frac{\pi}{4}\) and slope of one of the lines is \(\frac{1}{2}\), find the slope of the other line.
Solution:
We know that the acute angle \(\theta\) between two lines with slopes \(m_1\) and \(m_2\) is given by
\(\tan \theta=\left|\frac{m_2-m_1}{1+m_1 m_2}\right| \dots(1)\)
Let \(m_1=\frac{1}{2}, m_2=m\) and \(\theta=\frac{\pi}{4}\).
Now, putting these values in (1), we get
\(
\tan \frac{\pi}{4}=\left|\frac{m-\frac{1}{2}}{1+\frac{1}{2} m}\right| \text { or } 1=\left|\frac{m-\frac{1}{2}}{1+\frac{1}{2} m}\right| \text {, }
\)
which gives \(\frac{m-\frac{1}{2}}{1+\frac{1}{2} m}=1\) or \(\frac{m-\frac{1}{2}}{1+\frac{1}{2} m}=-1\).
Therefore \(m=3\) or \(m=-\frac{1}{3}\).
Hence, slope of the other line is 3 or \(-\frac{1}{3}\). Fig below explains the reason of two answers.
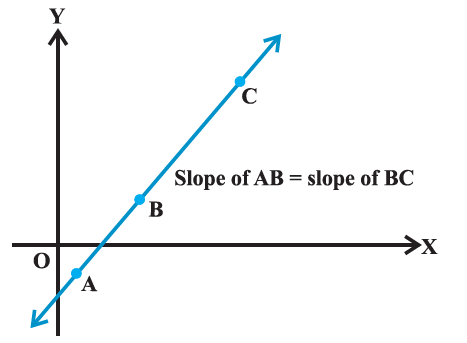
Collinearity of three points
We know that slopes of two parallel lines are equal. If two lines having the same slope pass through a common point, then two lines will coincide. Hence, if A, B and C are three points in the XY-plane, then they will lie on a line, i.e., three points are collinear (Fig below) if and only if slope of AB = slope of BC.
Example 13: Three points \(\mathrm{P}(h, k), \mathrm{Q}\left(x_1, y_1\right)\) and \(\mathrm{R}\left(x_2, y_2\right)\) lie on a line. Show that
\(
\left(h-x_1\right)\left(y_2-y_1\right)=\left(k-y_1\right)\left(x_2-x_1\right) .
\)
Solution:
Since points P, Q and R are collinear, we have
Slope of \(\mathrm{PQ}=\) Slope of \(\mathrm{QR}\), i.e., \(\frac{y_1-k}{x_1-h}=\frac{y_2-y_1}{x_2-x_1}\)
or \(\quad \frac{k-y_1}{h-x_1}=\frac{y_2-y_1}{x_2-x_1}\),
or \(\quad\left(h-x_1\right)\left(y_2-y_1\right)=\left(k-y_1\right)\left(x_2-x_1\right)\).
Example 14: In Fig below, time and distance graph of a linear motion is given. Two positions of time and distance are recorded as, when \(\mathrm{T}=0, \mathrm{D}=2\) and when \(\mathrm{T}=3, \mathrm{D}=8\). Using the concept of slope, find law of motion, i.e., how distance depends upon time.
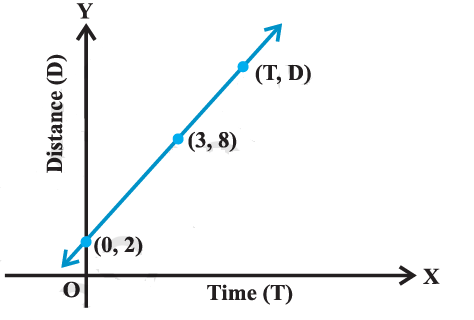
Let (T, D) be any point on the line, where \(\mathrm{D}\) denotes the distance at time T. Therefore, points \((0,2),(3,8)\) and ( T, D) are collinear so that
\(
\frac{8-2}{3-0}=\frac{\mathrm{D}-8}{\mathrm{~T}-3} \quad \text { or } \quad 6(\mathrm{~T}-3)=3(\mathrm{D}-8)
\)
or \(\quad \mathrm{D}=2(\mathrm{~T}+1)\),
which is the required relation.
Example 15: Prove that slope of a line remains same wen angle \(\theta\) is obtuse or when angle \(\theta\) is acute.
Solution: We know that a line is completely determined when we are given two points on it. Hence, we proceed to find the slope of a line in terms of the coordinates of two points on the line.
Let \(P \left(x_1, y_1\right)\) and \(Q \left(x_2, y_2\right)\) be two points on non-vertical line \(l\) whose inclination is \(\theta\). Obviously, \(x_1 \neq x_2\), otherwise the line will become perpendicular to \(x\)-axis and its slope will not be defined. The inclination of the line \(l\) may be acute or obtuse. Let us take these two cases.
Draw perpendicular QR to \(x\)-axis and PM perpendicular to \(R Q\) as shown in Figs. 10.3 (i) and (ii).
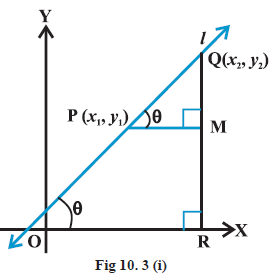
Case I: When angle \(\theta\) is acute:
In Fig 10.3 (i), \(\angle MPQ =\theta \dots(1)\).
Therefore, slope of line \(l=m=\tan \theta\).
But in \(\triangle MPQ\), we have \(\tan \theta=\frac{ MQ }{ MP }=\frac{y_2-y_1}{x_2-x_1} \dots(2)\).
From equations (1) and (2), we have
\(
m=\frac{y_2-y_1}{x_2-x_1} .
\)
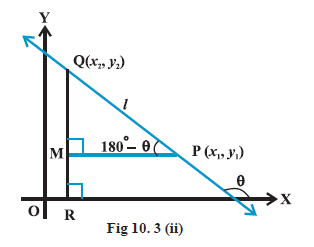
Case II: When angle \(\theta\) is obtuse:
In Fig 10.3 (ii), we have
\(
\angle MPQ =180^{\circ}-\theta \text {. }
\)
Therefore, \(\theta=180^{\circ}-\angle MPQ\).
Now, slope of the line \(l\)
\(
\begin{aligned}
m & =\tan \theta \\
& =\tan \left(180^{\circ}-\angle MPQ \right)=-\tan \angle MPQ \\
& =-\frac{ MQ }{ MP }=-\frac{y_2-y_1}{x_1-x_2}=\frac{y_2-y_1}{x_2-x_1} .
\end{aligned}
\)
Consequently, we see that in both the cases the slope \(m\) of the line through the points \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) is given by \(m=\frac{y_2-y_1}{x_2-x_1}\).