Sample Paper
These 20 Sample questions are taken from the JEE (Main) 2021 Math Entrance Paper (Section-A)
Q1. The sum of solutions of the equation \(\frac{\cos x}{1+\sin x}=|\tan 2 x|, x \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)-\left\{\frac{\pi}{4},-\frac{\pi}{4}\right\}\) is :
(1) \(-\frac{11 \pi}{30}\)
(2) \(\frac{\pi}{10}\)
(3) \(-\frac{7 \pi}{30}\)
(4) \(-\frac{\pi}{15}\)
Answer: 1
Solution:
\(\begin{aligned}&\frac{\cos x}{1+\sin x}=|\tan 2 x| \\
&\Rightarrow \frac{\cos ^{2} x / 2-\sin ^{2} x / 2}{(\cos x / 2+\sin x / 2)}=|\tan 2 x| \\
&\Rightarrow \tan ^{2}\left(\frac{\pi}{4}-\frac{x}{2}\right)=\tan ^{2} 2 x \\
&\Rightarrow 2 x=n \pi \pm\left(\frac{\pi}{4}-\frac{x}{2}\right) \\
&\Rightarrow x=\frac{-3 \pi}{10}, \frac{-\pi}{6}, \frac{\pi}{10} \\
&\text { The Sum of solutions of the equation}= \frac{-3 \pi}{10}+\frac{-\pi}{6}+\frac{\pi}{10} = \frac{-11 \pi}{30}
\end{aligned}\)
Q2. The mean and standard deviation of 20 observations were calculated as 10 and \(2.5\) respectively. It was found that by mistake one data value was taken as 25 instead of 35 . If \(\alpha\) and \(\sqrt{\beta}\) are the mean and standard deviation respectively for correct data, then \((\alpha, \beta)\) is:
(1) \((11,26)\)
(2) \((10.5,25)\)
(3) \((11,25)\)
(4) \((10.5,26)\)
Answer: 4
Q3. On the ellipse \(\frac{x^{2}}{8}+\frac{y^{2}}{4}=1\) let \(P\) be a point in the second quadrant such that the tangent at \(P\) to the ellipse is perpendicular to the line \(x+2 y=0\). Let \(S\) and \(S^{\prime}\) be the foci of the ellipse and \(e\) be its eccentricity. If \(\mathrm{A}\) is the area of the triangle SPS’ then, the value of \(\left(5-\mathrm{e}^{2}\right) \mathrm{A}\) is:
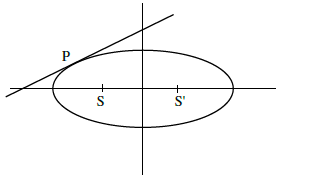
(1) 6
(2) 12
(3) 14
(4) 24
Answer: 1
Solution:
Equation of tangent : \(y=2 x+6\) at \(\mathrm{P}\)
\(
\begin{aligned}
&\therefore \mathrm{P}(-8 / 3,2 / 3) \\
&\mathrm{e}=\frac{1}{\sqrt{2}} \\
&\mathrm{~S} \& \mathrm{~S}^{\prime}=(-2,0) \&(2,0)
\end{aligned}
\)
Area of \(\triangle \mathrm{SPS}^{\prime}=\frac{1}{2} \times 4 \times \frac{2}{3}\)
\(A=\frac{4}{3}\)
\(\therefore\left(5-\mathrm{e}^{2}\right) \mathrm{A}=\left(5-\frac{1}{2}\right) \frac{4}{3}=6\)
Q4. Let \(y=y(x)\) be a solution curve of the differential equation \((y+1) \tan ^{2} x d x+\tan x d y+y d x=0\) \(x \in\left(0, \frac{\pi}{2}\right)\). If \(\lim _{x \rightarrow 0+} x y(x)=1\), then the value of \(\mathrm{y}\left(\frac{\pi}{4}\right)\) is:
(1) \(-\frac{\pi}{4}\)
(2) \(\frac{\pi}{4}-1\)
(3) \(\frac{\pi}{4}+1\)
(4) \(\frac{\pi}{4}\)
Answer: 4
Solution:
\((y+1) \tan ^{2} x d x+\tan x d y+y d x=0\)
\(\frac{d y}{d x}+\frac{\sec ^{2} x}{\tan x} \cdot y=-\tan x\)
\(I F=e^{\int \frac{\sec ^{2} x}{\tan x} d x}=e^{\ln \tan x}=\tan x\)
\(\therefore y \tan x=-\int \tan ^{2} x d x\)
\(y \tan x=-\tan x+x+C\)
\(\mathrm{y}=-1+\frac{\mathrm{x}}{\tan \mathrm{x}}+\frac{\mathrm{C}}{\tan \mathrm{x}}\)
\(\lim _{x \rightarrow 0} x y=-x+\frac{x^{2}}{\tan x}+\frac{C x}{\tan x}=1\) or \(\mathrm{C}=1\)
\(y(x)=\cot x+x \cot x-1\)
\(y\left(\frac{\pi}{4}\right)=\frac{\pi}{4}\)
Q5. Let \(\mathrm{A}\) and \(\mathrm{B}\) be independent events such that \(\mathrm{P}(\mathrm{A})=\mathrm{p}, \mathrm{P}(\mathrm{B})=2 \mathrm{p}\). The largest value of \(\mathrm{p}\), for which \(P\) (exactly one of \(A, B\) occurs \()=\frac{5}{9}\), is:
(1) \(\frac{1}{3}\)
(2) \(\frac{2}{9}\)
(3) \(\frac{4}{9}\)
(4) \(\frac{5}{12}\)
Answer: 4
Solution:
\(\mathrm{P}(\) Exactly one of \(\mathrm{A}\) or \(\mathrm{B})\)
\(
\begin{aligned}
&=\mathrm{P}(\mathrm{A} \cap \overline{\mathrm{B}})+\mathrm{P}(\overline{\mathrm{A}} \cap \mathrm{B})=\frac{5}{9} \\
&=\mathrm{P}(\mathrm{A}) \mathrm{P}(\overline{\mathrm{B}})+\mathrm{P}(\overline{\mathrm{A}}) \mathrm{P}(\mathrm{B})=\frac{5}{9} \\
&\Rightarrow \mathrm{P}(\mathrm{A})(1-\mathrm{P}(\mathrm{B}))+(1-\mathrm{P}(\mathrm{A})) \mathrm{P}(\mathrm{B})=\frac{5}{9} \\
&\Rightarrow \mathrm{p}(1-2 \mathrm{p})+(1-\mathrm{p}) 2 \mathrm{p}=\frac{5}{9} \\
&\Rightarrow 36 \mathrm{p}^{2}-27 \mathrm{p}+5=0 \\
&\Rightarrow \mathrm{p}=\frac{1}{3} \text { or } \frac{5}{12} \\
&\mathrm{p}_{\max }=\frac{5}{12}
\end{aligned}
\)
Q6. Let \(\theta \in\left(0, \frac{\pi}{2}\right)\). If the system of linear equations
\(\left(1+\cos ^{2} \theta\right) x+\sin ^{2} \theta y+4 \sin 3 \theta z=0\)
\(\cos ^{2} \theta x+\left(1+\sin ^{2} \theta\right) y+4 \sin 3 \theta z=0\)
\(\cos ^{2} \theta \mathrm{x}+\sin ^{2} \theta \mathrm{y}+(1+4 \sin 3 \theta) \mathrm{z}=0\); has a non-trivial solution, then the value of \(\theta\) is:
(1) \(\frac{4 \pi}{9}\)
(2) \(\frac{7 \pi}{18}\)
(3) \(\frac{\pi}{18}\)
(4) \(\frac{5 \pi}{18}\)
Answer: 2
Q7. Let \(f(x)=\cos \left(2 \tan ^{-1} \sin \left(\cot ^{-1} \sqrt{\frac{1-x}{x}}\right)\right)\), \(0<x<1\). Then :
(1) \((1-x)^{2} f^{\prime}(x)-2(f(x))^{2}=0\)
(2) \((1+x)^{2} f^{\prime}(x)+2(f(x))^{2}=0\)
(3) \((1-x)^{2} f^{\prime}(x)+2(f(x))^{2}=0\)
(4) \((1+x)^{2} f^{\prime}(x)-2(f(x))^{2}=0\)
Answer: 3
Solution:
\(
f(x)=\cos \left(2 \tan ^{-1} \sin \left(\cot ^{-1} \sqrt{\frac{1-x}{x}}\right)\right)
\)
\(\cot ^{-1} \sqrt{\frac{1-x}{x}}=\sin ^{-1} \sqrt{x}\)
or \(\mathrm{f}(\mathrm{x})=\cos \left(2 \tan ^{-1} \sqrt{\mathrm{x}}\right)\)
\(=\cos \tan ^{-1}\left(\frac{2 \sqrt{x}}{1-x}\right)\)
\(f(x)=\frac{1-x}{1+x}\)
Now \(\mathrm{f}^{\prime}(\mathrm{x})=\frac{-2}{(1+\mathrm{x})^{2}}\)
or \(f^{\prime}(x)(1-x)^{2}=-2\left(\frac{1-x}{1+x}\right)^{2}\)
or \((1-x)^{2} f^{\prime}(x)+2(f(x))^{2}=0\). Therefore Option 3 is the right answer.
Q8. The sum of the series \(\frac{1}{x+1}+\frac{2}{x^{2}+1}+\frac{2^{2}}{x^{4}+1}+\ldots .+\frac{2^{100}}{x^{2^{100}}+1}\); when \(x=2\) is:
(1) \(1+\frac{2^{101}}{4^{101}-1}\)
(2) \(1+\frac{2^{100}}{4^{101}-1}\)
(3) \(1-\frac{2^{100}}{4^{100}-1}\)
(4) \(1-\frac{2^{101}}{4^{101}-1}\)
Answer: 4
Q9. If \({ }^{20} C_{r}\) is the co-efficient of \(x^{r}\) in the expansion of \((1+\mathrm{x})^{20}\), then the value of \(\sum_{\mathrm{r}=0}^{20} \mathrm{r}^{2 20} \mathrm{C}_{\mathrm{r}}\) is equal to:
(1) \(420 \times 2^{19}\)
(2) \(380 \times 2^{19}\)
(3) \(380 \times 2^{18}\)
(4) \(420 \times 2^{18}\)
Answer: 4
Solution:
\(
\begin{aligned}
&\sum_{\mathrm{r}=0}^{20} \mathrm{r}^{2} \cdot{ }^{20} \mathrm{C}_{\mathrm{r}} \\
&\sum(4(\mathrm{r}-1)+\mathrm{r}) \cdot{ }^{20} \mathrm{C}_{\mathrm{r}} \\
&\sum \mathrm{r}(\mathrm{r}-1) \cdot \frac{20 \times 19}{\mathrm{r}(\mathrm{r}-1)} \cdot{ }^{18} \mathrm{C}_{\mathrm{r}}+\mathrm{r} \cdot \frac{20}{\mathrm{r}} \cdot \sum^{19} \mathrm{C}_{\mathrm{r}-1} \\
&\Rightarrow 20 \times 19.2^{18}+20.2^{19} \\
&\Rightarrow 420 \times 2^{18}
\end{aligned}
\)
Q10. Out of all the patients in a hospital 89% are found to be suffering from heart ailment and 98% are suffering from lungs infection. If K% of them are suffering from both ailments, then K can not belong to the set:
(1) {80, 83, 86, 89}
(2) {84, 86, 88, 90}
(3) {79, 81, 83, 85}
(4) {84, 87, 90, 93}
Answer: 3
Solution:
\(\begin{aligned}
&n(A \cup B) \geq n(A)+n(B)-n(A \cap B) \\
&100 \geq 89+98-n(A \cup B) \\
&n(A \cup B) \geq 87 \\
&87 \leq n(A \cup B) \leq 89
\end{aligned}\);
Therefore, Option 3 is the right answer.
Q11. The equation \(\arg \left(\frac{\mathrm{z}-1}{\mathrm{z}+1}\right)=\frac{\pi}{4}\) represents a circle with:
(1) centre at \((0,-1)\) and radius \(\sqrt{2}\)
(2) centre at \((0,1)\) and radius \(\sqrt{2}\)
(3) centre at \((0,0)\) and radius \(\sqrt{2}\)
(4) centre at \((0,1)\) and radius 2
Answer: 2
Q12. Let \(\overrightarrow{\mathrm{a}}=\hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}}\) and \(\overrightarrow{\mathrm{b}}=\hat{\mathrm{j}}-\hat{\mathrm{k}}\). If \(\overrightarrow{\mathrm{c}}\) is a vector such that \(\vec{a} \times \vec{c}=\vec{b}\) and \(\vec{a} \cdot \vec{c}=3\), then \(\vec{a} \cdot(\vec{b} \times \vec{c})\) is equal to :
(1) \(-2\)
(2) \(-6\)
(3) 6
(4) 2
Answer: 1
Q13. If a line along a chord of the circle \(4 \mathrm{x}^{2}+4 \mathrm{y}^{2}+120 \mathrm{x}+675=0\), passes through the point \((-30,0)\) and is tangent to the parabola \(y^{2}=30 x\), then the length of this chord is:
(1) 5
(2) 7
(3) \(5 \sqrt{3}\)
(4) \(3 \sqrt{5}\)
Answer: 4
Q14. The value of \(\int_{-1 / \sqrt{2}}^{1 / \sqrt{2}}\left(\left(\frac{x+1}{x-1}\right)^{2}+\left(\frac{x-1}{x+1}\right)^{2}-2\right)^{1 / 2} d x\) is:
(1) \(\log _{e} 4\)
(2) \(\log _{\mathrm{e}} 16\)
(3) \(2 \log _{\mathrm{e}} 16\)
(4) \(4 \log _{\mathrm{e}}(3+2 \sqrt{2})\)
Answer: 2
Solution:
\(
\begin{aligned}
&I=\int_{-1 / \sqrt{2}}^{1 / \sqrt{2}}\left(\left(\frac{x+1}{x-1}-\frac{x-1}{x+1}\right)^{2}\right)^{1 / 2} d x \\
&I=\int_{-1 / \sqrt{2}}^{1 / \sqrt{2}}\left|\frac{4 x}{x^{2}-1}\right| d x \Rightarrow I=2.4 \int_{0}^{1 / \sqrt{2}}\left|\frac{x}{x^{2}-1}\right| d x \\
&\Rightarrow I=-4 \int_{0}^{1 / \sqrt{2}} \frac{2 x}{x^{2}-1} d x \Rightarrow I=-4 \ln \left|x^{2}-1\right|_{0}^{1 / \sqrt{2}} \\
&\Rightarrow I=4 \ln 2 \Rightarrow I=\ln 16
\end{aligned}
\)
Q15. A plane \(P\) contains the line \(x+2 y+3 z+1=0=x-y-z-6\) and is perpendicular to the plane \(-2 \mathrm{x}+\mathrm{y}+\mathrm{z}+8=0\). Then which of the following points lies on P?
(1) \((-1,1,2)\)
(2) \((0,1,1)\)
(3) \((1,0,1)\)
(4) \((2,-1,1)\)
Answer: 2
Q16. If \(\mathrm{A}=\left(\begin{array}{ll}\frac{1}{\sqrt{5}} & \frac{2}{\sqrt{5}} \\ \frac{-2}{\sqrt{5}} & \frac{1}{\sqrt{5}}\end{array}\right), \mathrm{B}=\left(\begin{array}{ll}1 & 0 \\ i & 1\end{array}\right), i=\sqrt{-1}\), and \(\mathrm{Q}=\mathrm{A}^{\mathrm{T}} \mathrm{BA}\), then the inverse of the matrix \(\mathrm{A} \mathrm{Q}^{2021} \mathrm{~A}^{\mathrm{T}}\) is equal to:
(1) \(\left(\begin{array}{cc}\frac{1}{\sqrt{5}} & -2021 \\ 2021 & \frac{1}{\sqrt{5}}\end{array}\right)\)
(2) \(\left(\begin{array}{cc}1 & 0 \\ -2021 i & 1\end{array}\right)\)
(3) \(\left(\begin{array}{cc}1 & 0 \\ 2021 i & 1\end{array}\right)\)
(4) \(\left(\begin{array}{cc}1 & -2021 i \\ 0 & 1\end{array}\right)\)
Answer: 2
Q17. If the sum of an infinite GP a, ar, \(a r^{2}, a r^{3}, \ldots\) is 15 and the sum of the squares of its each term is 150 , then the sum of \(a r^{2}, a r^{4}, a r^{6}, \ldots\) is:
(1) \(\frac{5}{2}\)
(2) \(\frac{1}{2}\)
(3) \(\frac{25}{2}\)
(4) \(\frac{9}{2}\)
Answer: 2
Q18. The value of \(\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{r=0}^{2 n-1} \frac{n^{2}}{n^{2}+4 r^{2}}\) is:
(1) \(\frac{1}{2} \tan ^{-1}(2)\)
(2) \(\frac{1}{2} \tan ^{-1}(4)\)
(3) \(\tan ^{-1}(4)\)
(4) \(\frac{1}{4} \tan ^{-1}(4)\)
Answer: 2
Solution:
\begin{aligned}
&\mathrm{L}=\lim _{\mathrm{n} \rightarrow \infty} \frac{1}{\mathrm{n}} \cdot \sum_{\mathrm{r}=0}^{2 \mathrm{n}-1} \frac{1}{1+4\left(\frac{\mathrm{r}}{\mathrm{n}}\right)^{2}} \\
&\Rightarrow \mathrm{L}=\int_{0}^{2} \frac{1}{1+4 \mathrm{x}^{2}} \mathrm{dx} \\
&\Rightarrow \mathrm{L}=\left.\frac{1}{2} \tan ^{-1}(2 \mathrm{x})\right|_{0} ^{2} \Rightarrow \mathrm{L}=\frac{1}{2} \tan ^{-1} 4
\end{aligned}
\)
Q19. Let \(\mathrm{ABC}\) be a triangle with \(\mathrm{A}(-3,1)\) and \(\angle \mathrm{ACB}=\theta, 0<\theta<\frac{\pi}{2}\). If the equation of the median through \(\mathrm{B}\) is \(2 \mathrm{x}+\mathrm{y}-3=0\) and the equation of angle bisector of \(C\) is \(7 x-4 y-1=0\), then \(\tan \theta\) is equal to:
(1) \(\frac{1}{2}\)
(2) \(\frac{3}{4}\)
(3) \(\frac{4}{3}\)
(4) 2
Answer: 3
Q20. If the truth value of the Boolean expression \(((\mathrm{p} \vee \mathrm{q}) \wedge(\mathrm{q} \rightarrow \mathrm{r}) \wedge(\sim \mathrm{r})) \rightarrow(\mathrm{p} \wedge \mathrm{q})\) is false, then the truth values of the statements \(p, q, r\) respectively can be:
(1) \(\mathrm{T} \mathrm{F} \mathrm{}\)
(2) \(\mathrm{FFT}\)
(3) T FF
(4) F T F
Answer: 3