How to decompose a vector into x and y components

It is often useful to decompose a vector into \(x\) and \(y\) components, i.e. find two forces such that one is in the \(x\) direction, the other is in the \(y\) direction, and the vector sum of the two forces is equal to the original force.

Let us assume we have a force \(\mathbf{F}\) that makes an angle of \(30^{\circ}\) with the positive \(x\) axis, as shown below:

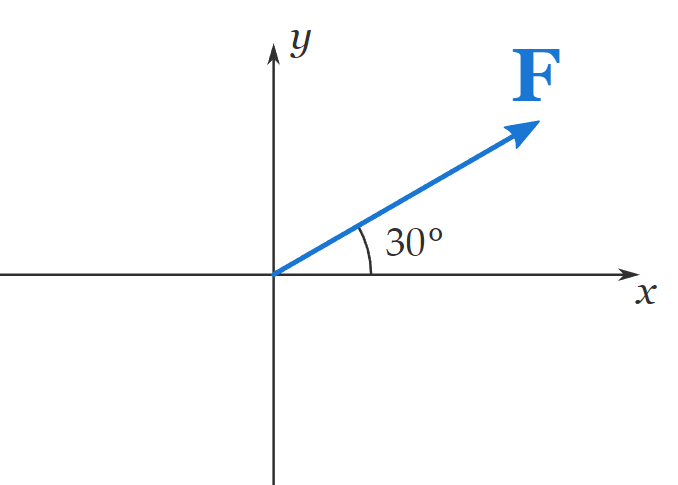
We want to decompose \(\mathbf{F}\) into \(x\) and \(y\) components.
The first thing we need to do is to represent the two components on the \(x y\)-plane. We do this by dropping two perpendiculars from the head of \(\mathbf{F}\): one to the \(x\) axis, the other to the \(y\) axis. And we join the origin of the \(x y\)-plane with the \(x\)-intercept to represent the \(x\) component of \(\mathbf{F}\). Again, we join the origin with the \(y\)-intercept to represent the \(y\) component of \(\mathbf{F}\):

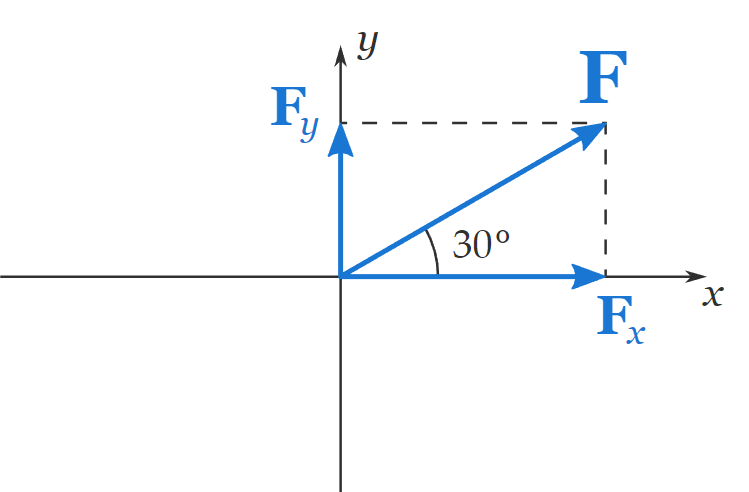
\(\mathbf{F}_x\) and \(\mathbf{F}_y\) are two vectors, i.e. they both have a magnitude and a direction. However, since \(\mathbf{F}_x\) and \(\mathbf{F}_y\) are in the directions of the \(x\) and \(y\) axes, they are commonly expressed by the magnitude alone, preceded by a positive or negative sign: positive when they point in the positive directions, and negative when they point in the negative directions of the \(x\) and \(y\) axes.

In our example \(F_x\) and \(F_y\) are positive because both point in the positive directions of the \(x\) and \(y\) axes.
The positive values of \(F_x\) and \(F_y\) can be found using trigonometry:
\(
\begin{aligned}
&F_x=F \cos 30^{\circ} \\
&F_y=F \sin 30^{\circ}
\end{aligned}
\)
To keep it simple, just remember that if a component is adjacent to the angle, then it is \(\cos\), otherwise, it is \(\sin\).

Often \(F_x\) will be the component adjacent to the angle, so it will be \(\cos\), and \(F_y\) will be sin.

Example 1: Find the x and y components of the vector shown below.

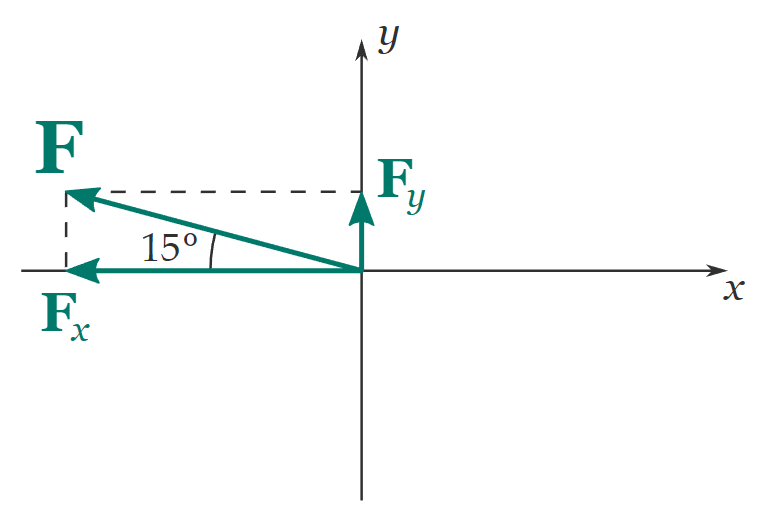
Solution: 

In this case \(F_x\) is negative because it points in the negative direction of the \(x\) axis.
Therefore:
\(
\begin{aligned}
&F_x=-F \cos 15^{\circ} \\
&F_y=F \sin 15^{\circ}
\end{aligned}
\)
Notice the minus sign before \(F \cos 15^{\circ}\) which we have added to make \(F_x\) negative.
You have to be very careful if your angle is not between \(0^{\circ}\) and \(90^{\circ}\), because the sin or(and) cos of that angle may be already negative, so the product is also negative and you don’t need to add a minus sign.

To be on the safe side, we recommend always work with angles between \(0^{\circ}\) and \(90^{\circ}\), so that the sin and \(\cos\) are always positive, and therefore the product is also always positive.

Example 2: Find the x and y components of the vector shown below.

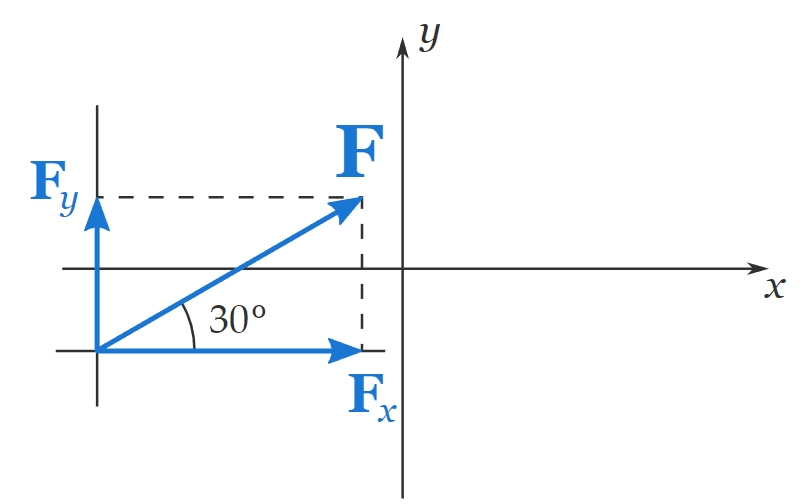
Solution: 

\(
\begin{aligned}
&F_x=F \cos 30^{\circ} \\
&F_y=F \sin 30^{\circ}
\end{aligned}
\)

Example 3: A force of \(29 \mathrm{~N}\) is in the direction of the negative \(x\) axis. Find the \(x\) and \(y\) components of the force.

Solution:

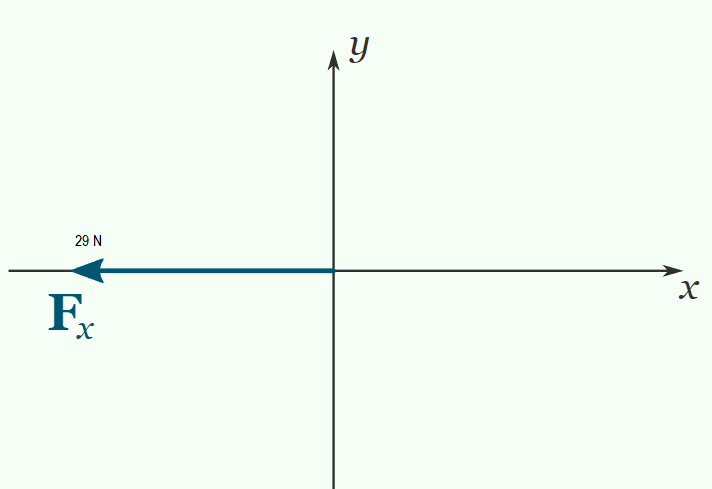
\(F_x\) is negative, and has the same magnitude as the force \((29 \mathrm{~N}) . F_y\) is zero.
\(
\begin{aligned}
&F_x=-29 \mathrm{~N} \\
&F_y=0 \mathrm{~N}
\end{aligned}
\)

Example 4: A force of \(114 \mathrm{~N}\) makes an angle of \(67^{\circ}\) with the positive \(x\) axis. Decompose the force into \(x\) and \(y\) components.

Solution:

\(
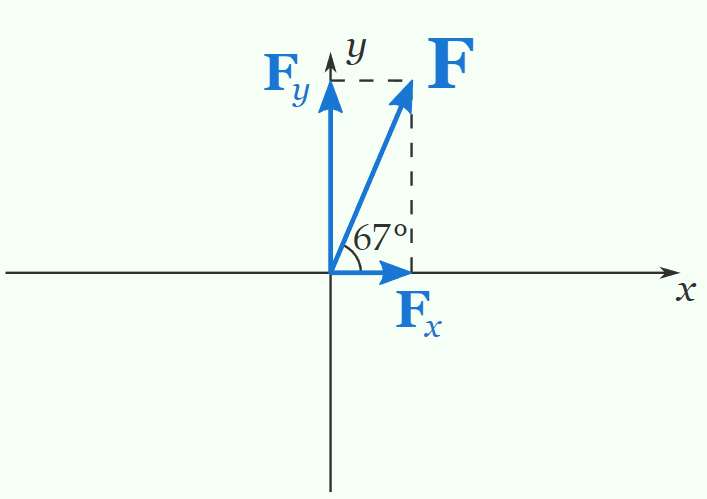
\begin{aligned}
&F_x=F \cos 67^{\circ}=44.5 \mathrm{~N} \\
&F_y=F \sin 67^{\circ}=105 \mathrm{~N}
\end{aligned}
\)

Example 5: A force makes an angle of \(221^{\circ}\) with the positive \(x\) axis. Assuming the force has magnitude \(3.1 \times 10^3 \mathrm{~N}\), find the \(x\) and \(y\) components.

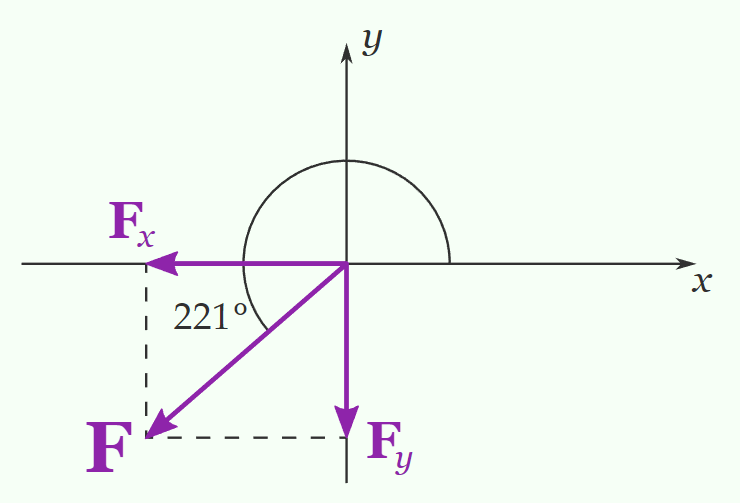
Solution:

Instead of dealing with the \(221^{\circ}\) angle, we want to deal with the \(41^{\circ}\) angle \(\left(221^{\circ}-180^{\circ}\right)\) that the force makes with the negative \(x\) axis:

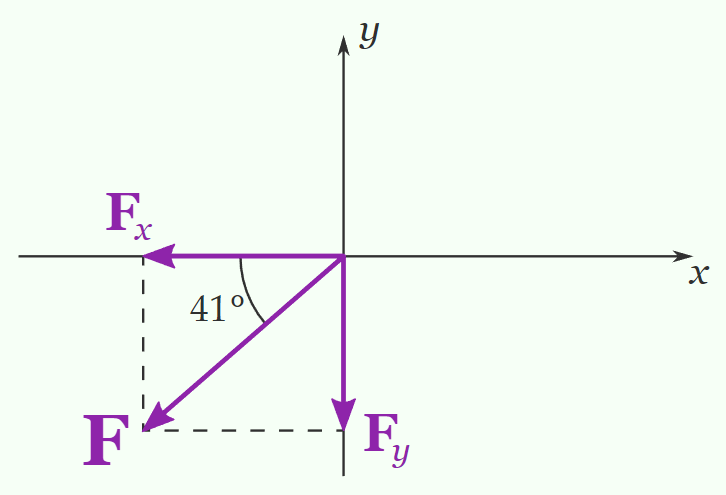
As you can see, both \(F_x\) and \(F_y\) are negative:
\(
\begin{aligned}
&F_x=-F \cos 41^{\circ}=-2.3 \times 10^3 \mathrm{~N} \\
&F_y=-F \sin 41^{\circ}=-2.0 \times 10^3 \mathrm{~N}
\end{aligned}
\)

Example 6: A \(90.0 \mathrm{~N}\) force makes an angle of \(33^{\circ}\) with the positive \(y\) direction. Calculate the \(x\) and \(y\) components of the force.

Solution:

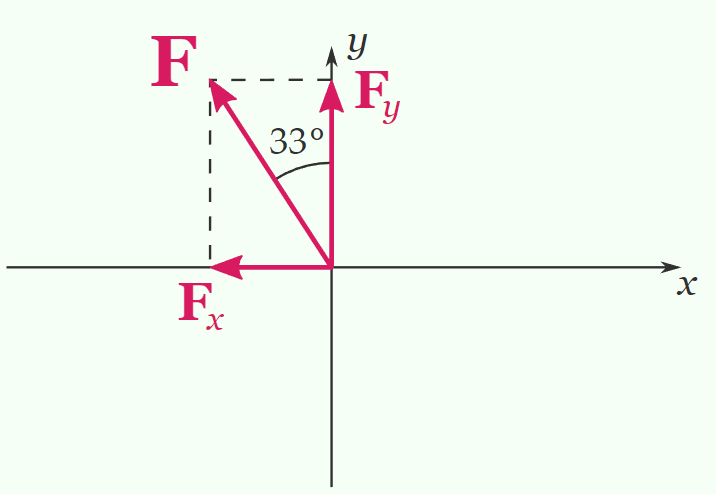
In this case \(F_y\) is adjacent to the angle, therefore its magnitude is the force times the \(\cos\) of the angle, while the magnitude of \(F_x\) is the force times the sin.
Also notice that \(F_x\) is negative:
\(
\begin{aligned}
&F_x=-F \sin 33^{\circ}=-49.0 \mathrm{~N} \\
&F_y=F \cos 33^{\circ}=75.5 \mathrm{~N}
\end{aligned}
\)
Alternatively you could have considered the \(57^{\circ}\) angle \(\left(90^{\circ}-33^{\circ}\right)\) which \(\mathbf{F}\) makes with \(\mathbf{F}_x\). That way \(\mathbf{F}_x\) would have been adjacent to the angle.

Example 7: A force that has magnitude \(3.21 \times 10^4 \mathrm{~N}\) makes an angle of \(-50^{\circ}\) with the positive \(x\) axis. Determine the components.

Solution:

\(
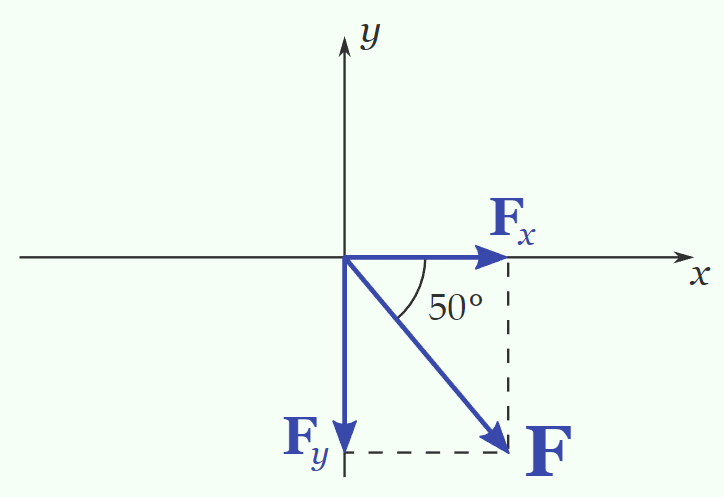
\begin{aligned}
&F_x=F \cos 50^{\circ}=2.06 \times 10^4 \mathrm{~N} \\
&F_y=-F \sin 50^{\circ}=-2.46 \times 10^4 \mathrm{~N}
\end{aligned}
\)

How to Find Resultant Vector given the x-y Component?

Follow the following rules as shown in the figure below.

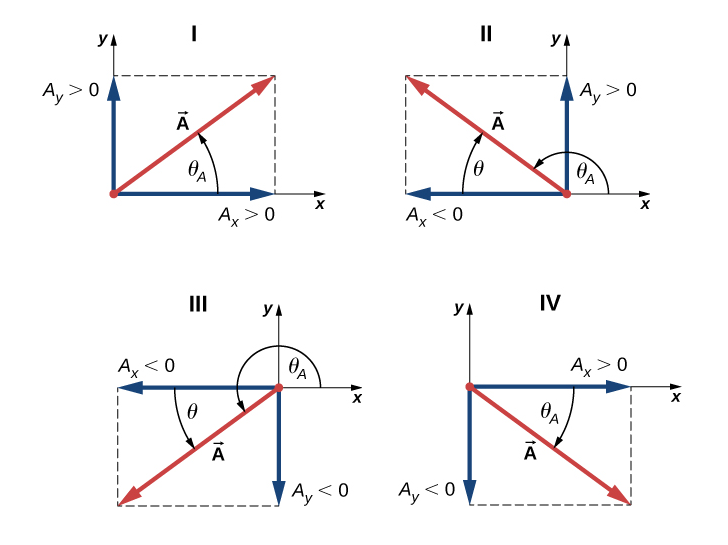
Magnitude of the resultant vector in 2 dimension

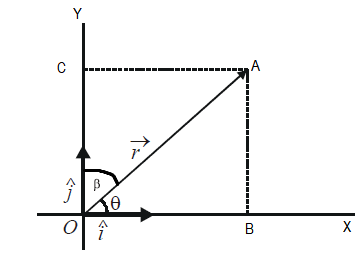
Let \(\theta\) be the angle that \(\vec{r}\) makes with \(\hat{i}\)
\(
\begin{aligned}
O B &=|\vec{r}| \cos \theta \\
O C &=|\vec{r}| \sin \theta
\end{aligned}
\)

The figure above shows a vector \(\vec{r}=\overrightarrow{O A}\) in the \(X-Y\) plane drawn from the origin \(O\). The vector makes an angle \(\theta\) with the \(X\)-axis and \(\beta\) with the \(Y\)-axis. Draw perpendiculars \(A B\) and \(A C\) from \(A\) to the \(X\) and \(Y\) axes respectively. The length \(O B\) is called the projection of \(\overrightarrow{O A}\) on \(X\)-axis. Similarly \(O C\) is the projection of \(\overrightarrow{O A}\) on \(Y\)-axis. According to the rules of vector addition
\(
\vec{r}=\overrightarrow{O A}=\overrightarrow{O B}+\overrightarrow{O C} \text {. }
\)
Thus, we have resolved the vector \(\vec{r}\) into two parts, one along \(O X\) and the other along \(O Y\). The magnitude of the part along \(O X\) is \(O B=|\vec{r}| \cos \theta\) and the magnitude of the part along \(O Y\) is \(O C=|\vec{r}| \cos \beta\). If \(\hat{i}\) and \(\hat{j}\) denote vectors of unit magnitude along \(O X\) and \(O Y\) respectively, we get

\(
\overrightarrow{O B}=|\vec{r}| \cos \theta \hat{i} \text { and } \overrightarrow{O C}=|\vec{r}| \cos \beta \hat{j} 
\) (\(\cos \beta=\cos \left(90^{\circ}-\theta\right)=\sin \theta\))

So that  \(\vec{r}\) = \(=(|\vec{r}| \cos \theta) \hat{i}+(|\vec{r}| \sin \theta) \hat{j} =x \hat{i}+y \hat{j}\)

where \(x\) and \(y\) are referred to as the \(x\) and \(y\) components of \(\vec{r}\).

For 3-D space, we select three unit vectors \(\hat{i}, \hat{j}\), and  \(\hat{k}\) each perpendicular to the other two.

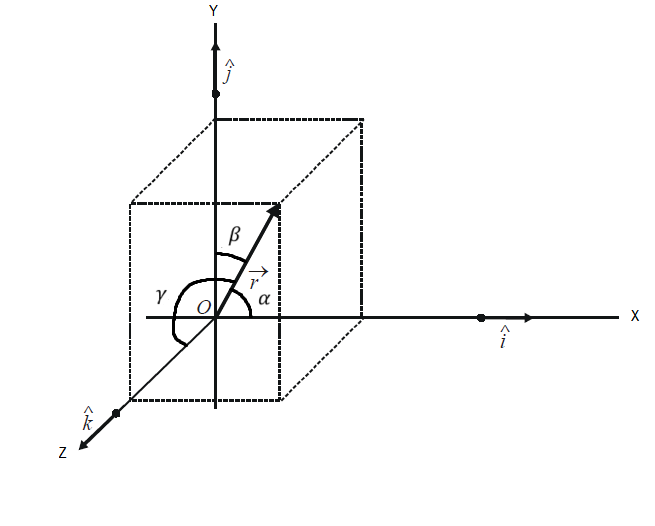
In this case, any vector \(\vec{r}\) will have three corresponding components, generally denoted by \(x, y\), and \(z\). We thus have
\(
\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}
\)

If \(\alpha, \beta, \gamma\) be the angles made by the vector \(\vec{r}\) with the three axes respectively, we get
\(
\vec{r}=|\vec{r}| \cos \alpha \hat{i}+|\vec{r}| \cos \beta \hat{j}+|\vec{r}| \cos \gamma \hat{k}
\)
where \( \hat{i},  \hat{i}\) and \( \hat{k}\) are the unit vectors along \(X, Y\) and \(Z\) axes respectively. The magnitude \((|\vec{r}| \cos \alpha)\) is called the component of \(\vec{r}\) along \(X\)-axis, \((|\vec{r}| \cos \beta)\) is called the component along \(Y\)-axis and \((|\vec{r}|\) cosy \()\) is called the component along \(Z\)-axis.

Magnitude of the resultant vector in 3 dimension

If a vector is resolved in three directions that are mutually perpendicular to each other, then the resolved components are called “Rectangular Components of Vector in three dimensions”. Therefore, if we resolve a vector in three directions, namely \(X, Y\) & \(Z\) axes, which are mutually perpendicular to each other, then component vectors so obtained are called rectangular components in three dimensions.
Consider that a vector \((\vec{A})\) is represented by \((O P)\) as shown in the figure.

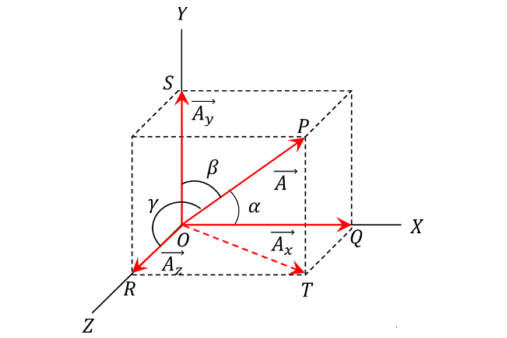
Taking \(O\) as origin, we construct a rectangular parallelopiped with its three edges along the three rectangular axes i.e. \(X, Y \& Z\) axes. Then, \((\vec{A})\) will represent the diagonal of the parallelopiped whose intercepts along \(X, Y \& Z\) axes are \(\left(\overrightarrow{A_x}\right),\left(\overrightarrow{A_y}\right) \&\left(\overrightarrow{A_z}\right)\) respectively.
Therefore, vectors \(\left(\vec{A}_x\right),\left(\vec{A}_y\right) \&\left(\vec{A_z}\right)\) are the three rectangular components of vector \((\vec{A})\).
Applying the triangle law of vectors, we will get 
\(
O P=O T+T P
\)
Applying the parallelogram law of vectors, we will get 
\(
O T=O R+O Q
\)
Therefore, \(O P=O R+O Q+T P\)
But, \(\quad T P=O S\)
Hence, \(\quad O P=O R+O Q+O S\)
So, \(\quad \vec{A}=\vec{A}_x+\vec{A}_y+\vec{A}_z\)
\(
=A_x \hat{i}+A_y \hat{j}+A_z \hat{k}
\)
Let, \((\alpha),(\beta)\) and \((\gamma)\) are the angles between the vector \((\vec{A})\) and \(X, Y \& Z\) axes respectively. Then we have
\(A_x=A \cos \alpha\)
\(A_y=A \cos \beta\)
\(A_z=A \cos \gamma\)

From the geometry of the figure, we can derive the magnitude of the vector in 3 dimension
\(
\begin{aligned}
&O P^2=O T^2+T P^2 \\
&=O Q^2+Q T^2+T P^2
\end{aligned}
\)
So, \(A^2=A_x^2+A_y{ }^2+A_z{ }^2\)
Or, \(\quad A=\sqrt{A_x{ }^2+A_y{ }^2+A_z{ }^2}\)

Similarly, a position vector \((\vec{r})\) in three dimensions can be expressed as 
\(
\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}
\)
Where, \((x),(y) \&(z)\) are the components of \((\vec{r})\) along \(X, Y \& Z\) axes respectively.

Example 8: A force of \(10.5 \mathrm{~N}\) acts on a particle along a direction making an angle of \(37^{\circ}\) with the vertical. Find the component of the force in the vertical direction.

Solution:

The component of the force in the vertical direction will be
\(
\begin{aligned}
F_{\perp} &=F \cos \theta=(10.5 \mathrm{~N})\left(\cos 37^{\circ}\right) \\
&=(10.5 \mathrm{~N}) \frac{4}{5}=8.40 \mathrm{~N} .
\end{aligned}
\)