Relative motion typically refers to, either the, relative position of one object as measured from the other object, or, relative velocity of one object with respect to another. The term relative is frequently used for comparison of displacement, velocity and acceleration of the two objects. The time rate of change of relative position of one object with respect to another is called relative velocity.

Relative velocity of \(A\) with respect to \(B\) is the rate at which relative position of \(A\) with respect to \(B\) is changing with time.
Relative Velocity = Velocity of the Body \(A\) – Velocity of the Body \(B\)
\(v_{A B}=v_A-v_B\)

Relative Velocity: One Dimensional motion

When a body only moves in a single direction with respect to the chosen axis, we call it motion in one dimension. Only the parameter of one particular direction changes while the rest remains the same. A ball thrown vertically upwards is a motion in one dimension; the parameter along the horizontal does not change while along the vertical, the velocity and the position of the ball change. A bike moving on a straight line with some acceleration is also an example of motion in one dimension.

If it is a one dimensional motion, we can treat the vectors as scalars just by assigning the positive sign to one direction and negative to the other. Let two objects \(A\) and \(B\) are moving along the + ve direction on \(X\)-axis. At time \(t\), their displacement from the origin be \(x_A\) and \(x_B\).

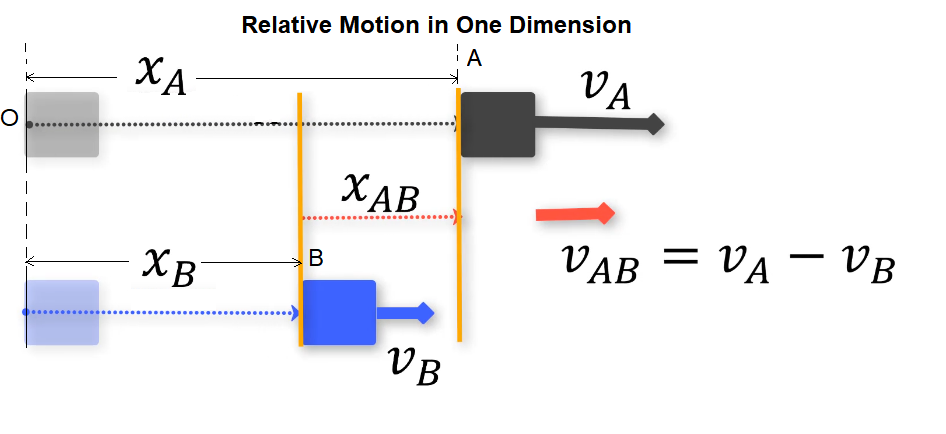
Note that \(A\) has only moved by a distance \(x_{A B}\) with respect to \(B\). So, \(B\) would observe \(A\) to be moving at a speed of \(v_{A B}\)

Their velocities are \({v}_A=\frac{d {x}_A}{d t}\) and \({v}_B=\frac{d {x}_B}{d t}\)
\(x_{A B} \quad\) : Position of \(A\) with respect to \(B\)
\(v_{A B} \quad\) : Velocity of \(A\) with respect to \(B\)
The displacement of \(A\) relative to \(B\),
\(
{x}_{A B}={x}_A-{x}_B
\)
Rate of change of relative displacement with respect to time is
\(
\frac{d\left({x}_{A B}\right)}{d t}=\frac{d}{d t}\left({x}_A-{x}_B\right) \Rightarrow \frac{d {x}_{A B}}{d t}=\frac{d {x}_A}{d t}-\frac{d {x}_B}{d t}
\)
\(\therefore \quad {v}_{A B}={v}_A-{v}_B\)
Similarly, relative acceleration of \(A\) with respect to \(B\) is
\(
{a}_{A B}={a}_A-{a}_B
\)
Further, we can see that \({v}_{A B}=-{v}_{B A}\) or \({a}_{B A}=-{a}_{A B}\)

Example 1: Aeroplane A flies with a velocity of \(450 \mathrm{~m} / \mathrm{s}\) to the north. Another aeroplane B travels at a velocity of \(500 \mathrm{~m} / \mathrm{s}\) to the south beside aeroplane \(A\). What will be the relative velocity of aeroplane \(A\) with respect to aeroplane \(B\) ?

Answer: Using the relative velocity formula, the relative velocity of aeroplane A with respect to the velocity of aeroplane B will be calculated as
\(
v_{A B}=v_A-v_B
\)
Substituting the values in the formula,
\(
v_{A B}=450 \mathrm{~m} / \mathrm{s}-(-500 \mathrm{~m} / \mathrm{s})=950 \mathrm{~m} / \mathrm{s}
\)
Therefore, the relative velocity of aeroplane A with respect to aeroplane B is \(950 \mathrm{~m} / \mathrm{s}\).

Example 2: A bus motorcycle travelling on the highway at a velocity of \(120 \mathrm{~km} / \mathrm{h}\) passes a car that is travelling at a velocity of \(90 \mathrm{~km} / \mathrm{h}\). What will be the relative velocity of the bus from the point of view of a passenger in the car?

Answer: Let us consider
Velocity of Bus: \(v_A\)
Velocity of Car: \(v_B\)

The velocity of the bus relative to the point of view of a passenger (who is a passenger in the car) will be calculated as
\(v_{A B}=v_A-v_B\)
\(v_{A B}=120 \mathrm{~km} / \mathrm{h}-90 \mathrm{~km} / \mathrm{h}\)
\(v_{A B}=30 \mathrm{~km} / \mathrm{h}\)

Thus, the velocity of the bus from the viewpoint of the passenger of the car is \(30 \mathrm{~km} / \mathrm{h}\).

Example 3: Suppose two cars A and B are moving with uniform velocities with respect to ground along parallel tracks and in the same direction. Let the velocities of \(\mathrm{A}\) and \(\mathrm{B}\) be \(35 \mathrm{~km} \mathrm{~h}^{-1}\) due east and \(40 \mathrm{~km} \mathrm{~h}^{-1}\) due east respectively. What is the relative velocity of car \(\mathrm{B}\) with respect to \(\mathrm{A}\) ?

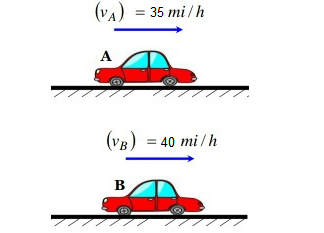
Answer: The relative velocity of \(\mathrm{B}\) with respect to \(\mathrm{A}, {v}_{B A}={v}_B-{v}_A=5 \mathrm{~km} \mathrm{~h}^{-1}\) due east Similarly, the relative velocity of A with respect to B i.e., \({v}_{A B}={v}_A-{v}_B=-5 \mathrm{~km} \mathrm{~h}^{-1}=5 \mathrm{~km} \mathrm{~h}^{-1}\) due west.

Example 4: How long will a boy sitting near the window of a train travelling at \(36 \mathrm{~km} \mathrm{~h}^{-1}\) see a train passing by in the opposite direction with a speed of \(18 \mathrm{~km} \mathrm{~h}^{-1}\). The length of the slow-moving train is \(90 \mathrm{~m}\).

Answer: The relative velocity of the slow-moving train with respect to the boy is \(v_{tb}=(18-(-36)) \mathrm{km} \mathrm{h}^{-1}=54 \mathrm{~km} \mathrm{~h}^{-1}=\) \(54 \times 5 / 18 \mathrm{~ms}^{-1}=15 \mathrm{~m} \mathrm{~s}^{-1}\)
Since the boy will watch the full length of the other train, to find the time taken to watch the full train:
We have, \(v_{tb}=\frac{\text { length of train }}{t}; 15=\frac{90}{t}\) or \(t=\frac{90}{15}=6 \mathrm{~s}\)

Example 5: A swimmer’s speed in the direction of flow of a river is \(12 \mathrm{~km} \mathrm{~h}^{-1}\). Against the direction of flow of the river the swimmer’s speed is \(6 \mathrm{~km} \mathrm{~h}^{-1}\). Calculate the swimmer’s speed in still water and the velocity of the river flow.

Answer: Let \(v_s\) and \(v_r\), represent the velocities of the swimmer and river respectively with respect to ground.
\(
v_{\mathrm{s}}+v_{\mathrm{r}}=12 \dots(1)
\)
\(
v_{\mathrm{s}}-v_{\mathrm{r}}=6 \dots(2)
\)
Adding the both equations (1) and (2)
\(
\begin{array}{l}
2 v_s=12+6=18 \mathrm{~km} \mathrm{~h}^{-1} \text { or } \\
v_s=9 \mathrm{~km} \mathrm{~h}^{-1}
\end{array}
\)
From Equation (1),
\(
\begin{array}{l}
9+v_{\mathrm{r}}=12 \text { or } \\
v_{\mathrm{r}}=3 \mathrm{~km} \mathrm{~h}^{-1}
\end{array}
\)

When the river flow and swimmer move in the same direction, the net velocity of swimmer is \(12 \mathrm{~km} \mathrm{ph}^{-1}\).

Example 6: Train A and train B are running on parallel tracks in the opposite directions with speeds of \(36 \mathrm{~km} / \mathrm{hour}\) and \(72 \mathrm{~km} /\) hour, respectively. A person is walking in train A in the direction opposite to its motion with a speed of \(1.8 \mathrm{~km} /\) hour. Speed (in \(\mathrm{ms}^{-1}\) ) of this person as observed from train B will be close to : (take the distance between the tracks as negligible)

Answer: 

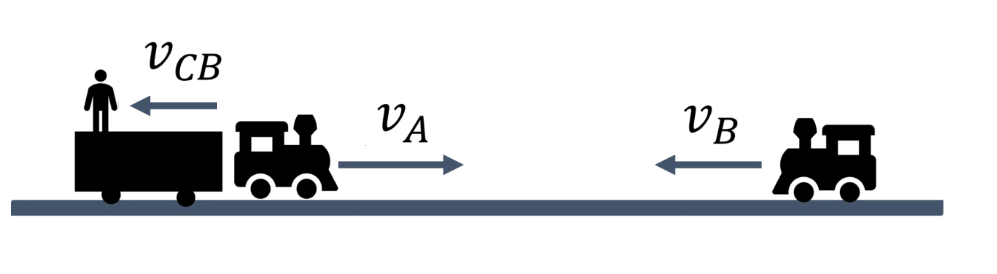
Step 1: Given Data
Train \(A\) and train \(B\) are in opposite directions.
Velocity of train \(A, v_A=36 \mathrm{~km} / \mathrm{hr}\)
Velocity of train \(B, v_B=-72 \mathrm{~km} / \mathrm{hr}\)
A person is walking on train \(A\) in the direction opposite to its motion.
The velocity of the person \(v_{C A}=-1.8 \mathrm{~km} / \mathrm{hr}\)
Let the velocity of the person observed from train B be \(v_{C B}\).
Step 2: Calculate the required velocity
The velocity of the person \(v_C=\) velocity of the person with respect to \(A, v_{C A}+\) velocity of \(A, v_A\)
Similarly, the velocity of the person with respect to \(B, v_{C B}=\) The velocity of the person \(v_C\) – velocity of \(B, v_B\)
\(
\begin{aligned}
\Rightarrow v_{C B} & =v_{C A}+v_A-v_B \\
& =-1.8+36-(-72) \\
& =106.2 \mathrm{~km} / \mathrm{hr}
\end{aligned}
\)
Step 3: Convert Velocity into \(m s^{-1}\)
Now,
\(
\begin{array}{l}
1 \mathrm{~km} / \mathrm{hr}=\frac{5}{18} \mathrm{~m} / \mathrm{s} \\
\therefore 106.2 \mathrm{~km} / \mathrm{hr}=\frac{5}{18} \times 106.2 \\
=29.5 \mathrm{~m} / \mathrm{s}
\end{array}
\)

Example 7: A police car was moving along a horizontal highway at \(47 \mathrm{~km} / \mathrm{h}\). It used a radar to measure the speed of a truck moving in the same direction. Given that the reading on the radar was \(50 \mathrm{~km} / \mathrm{~h}\), determine the actual speed of the truck.

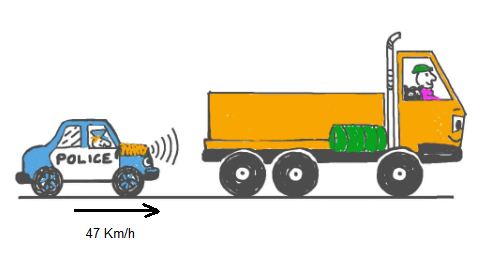
Answer: Relative velocity = \({v}_{t p}={v}_t-{v}_p\)
\(
v_p=47 \mathrm{~km} / \mathrm{h}
\)
\(
v_{t p}=50 \mathrm{~km} / \mathrm{h}
\)
\(
\begin{aligned}
50 & ={v}_t-47 \\
97 & ={v}_t
\end{aligned}
\)
Actual speed \(=97 \mathrm{~km} / \mathrm{h}\)

Example 8: Two cars \(A\) and \(B\) are moving in the same direction on a straight road, where the velocity of car \(B\) relative to car \(A\) is \(34 \mathrm{~km} / \mathrm{h}\). If car \(A\) slowed down to a quarter of its velocity, the velocity of car \(B\) relative to car \(A\) would be \(76 \mathrm{~km} / \mathrm{h}\). Determine the actinal speeds of the two cars \(v_A\) and \(v_B\).

Answer:

\(
\begin{array}{l}
v_{B A}=v_B-v_A \\
v_B-v_A=34 \dots(1) \\
v_B-\frac{1}{4} v_A=76 \dots(2)
\end{array}
\)
Solving equations (1) and (2) We get,
\(
v_A=56 \mathrm{~km} / \mathrm{h}
\)
\(
v_B=90 \mathrm{~km} / \mathrm{h}
\)

Reference Frames

To discuss relative motion in one or more dimensions, we first introduce the concept of reference frames. When we say an object has a certain velocity, we must state it has a velocity with respect to a given reference frame. In most examples we have examined so far, this reference frame has been Earth. If you say a person is sitting in a train moving at \(10 \mathrm{~m} / \mathrm{s}\) east, then you imply the person on the train is moving relative to the surface of Earth at this velocity, and Earth is the reference frame. In summary, all discussion of relative motion must define the reference frames involved. We now develop a method to refer to reference frames in relative motion.

Relative Velocity: Two Dimensional motion

When a particle’s kinematic parameters vary in both the horizontal and vertical direction, such a type of motion is known as motion in two dimensions. For example, A particle is projected at some angle with the horizontal it moves in both the direction, vertical and the horizontal, such type motion is known as motion in two dimensions.

\(
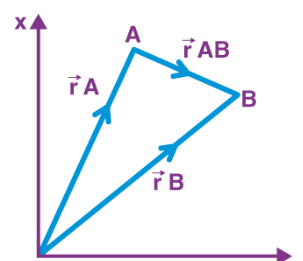
\vec{r}_{A B}=\vec{r}_A-\vec{r}_B
\)
Here, \(\vec{r}_A, \vec{r}_B\) are position vector of \(\mathrm{A}\) and \(\mathrm{B}\) w.r.t origin.
\(
\vec{V}_{A B}=\vec{V}_A-\vec{V}_B
\)
Here, \(\vec{V}_A\) and \(\vec{V}_B\) are the velocity w.r.t to ground.
\(
\begin{array}{l}
\vec{a}_{A B}=\frac{d}{d t} \overrightarrow{V_{A B}}=\frac{d}{d t} \vec{V}_A-\frac{d}{d t} \vec{V}_B \\
=\vec{a}_A-\vec{a}_B
\end{array}
\)
Here, \(\vec{a}_A, \vec{a}_B\), are the acceleration w.r.t to ground.

Example 9: A truck is traveling south at a speed of \(70 \mathrm{~km} / \mathrm{h}\) toward an intersection. A car is traveling east toward the intersection at a speed of \(80 \mathrm{~km} / \mathrm{h}\) (Figure). What is the velocity of the car relative to the truck?

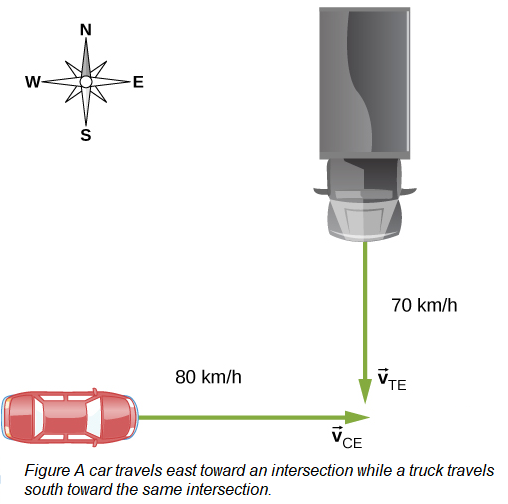
Answer: First, we must establish the reference frame common to both vehicles, which is Earth. Then, we write the velocities of each with respect to the reference frame of Earth, which enables us to form a vector equation that links the car, the truck, and Earth to solve for the velocity of the car with respect to the truck.

The velocity of the car with respect to Earth is \(\overrightarrow{\mathbf{v}}_{\mathrm{CE}}=80 \mathrm{~km} / \mathrm{h} \hat{\mathbf{i}}\). The velocity of the truck with respect to Earth is \(\overrightarrow{\mathbf{v}}_{\mathrm{TE}}=-70 \mathrm{~km} / \mathrm{h} \hat{\mathbf{j}}\). Using the velocity addition rule, the relative motion equation we are seeking is
\(
\overrightarrow{\mathbf{v}}_{\mathrm{CT}}=\overrightarrow{\mathbf{v}}_{\mathrm{CE}}+\overrightarrow{\mathbf{v}}_{\mathrm{ET}} 
\)
Here, \(\overrightarrow{\mathbf{v}}_{\mathbf{C T}}\) is the velocity of the car with respect to the truck, and Earth is the connecting reference frame. Since we have the velocity of the truck with respect to Earth, the negative of this vector is the velocity of Earth with respect to the truck: \(\overrightarrow{\mathbf{v}}_{\mathrm{ET}}=-\overrightarrow{\mathbf{v}}_{\mathrm{TE}}\). The vector diagram of this equation is shown in Figure below.

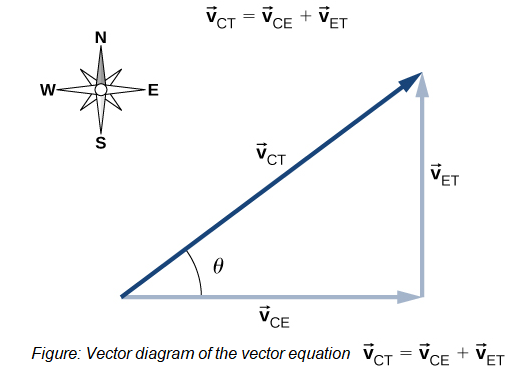
We can now solve for the velocity of the car with respect to the truck:
\(
\left|\overrightarrow{\mathbf{v}}_{\mathrm{CT}}\right|=\sqrt{(80.0 \mathrm{~km} / \mathrm{h})^2+(70.0 \mathrm{~km} / \mathrm{h})^2}=106 . \mathrm{km} / \mathrm{h}
\)
and
\(
\theta=\tan ^{-1}\left(\frac{70.0}{80.0}\right)=41.2^{\circ} \text { north of east. }
\)
Significance: Drawing a vector diagram showing the velocity vectors can help in understanding the relative velocity of the two objects.

Example 10: A boat heads north in still water at \(4.5 \mathrm{~m} / \mathrm{s}\) directly across a river that is running east at \(3.0 \mathrm{~m} / \mathrm{s}\). What is the velocity of the boat with respect to Earth?

Answer:

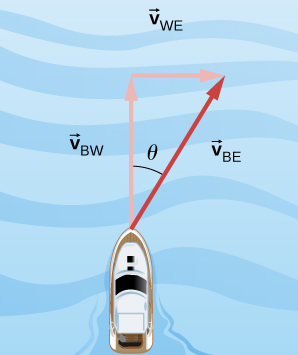
Labeling subscripts for the vector equation, we have \(\mathrm{B}=\) boat, \(\mathrm{W}=\) river, and \(\mathrm{E}=\) Earth. The vector equation becomes \(\vec{v}_{\mathrm{BE}}=\vec{v}_{\mathrm{BW}}+\vec{v}_{\mathrm{WE}}\). We have right triangle geometry shown in Figure. Solving for \(\vec{v}_{\mathrm{BE}}\), we have
\(
\begin{array}{l}
v_{\mathrm{BE}}=\sqrt{v_{\mathrm{BW}}^2+v_{\mathrm{WE}}^2}=\sqrt{4.5^2+3.0^2} \\
v_{\mathrm{BE}}=5.4 \mathrm{~m} / \mathrm{s}, \theta=\tan ^{-1}\left(\frac{3.0}{4.5}\right)=33.7^{\circ}
\end{array}
\)

Example 11: A pilot must fly his plane due north to reach his destination. The plane can fly at \(300 \mathrm{~km} / \mathrm{h}\) in still air. A wind is blowing out of the northeast at \(90 \mathrm{~km} / \mathrm{h}\). (a) What is the speed of the plane relative to the ground? (b) In what direction must the pilot head her plane to fly due north?

Answer: The pilot must point her plane somewhat east of north to compensate for the wind velocity. We need to construct a vector equation that contains the velocity of the plane with respect to the ground, the velocity of the plane with respect to the air, and the velocity of the air with respect to the ground. Since these last two quantities are known, we can solve for the velocity of the plane with respect to the ground. We can graph the vectors and use this diagram to evaluate the magnitude of the plane’s velocity with respect to the ground. The diagram will also tell us the angle the plane’s velocity makes with north with respect to the air, which is the direction the pilot must head her plane. The vector equation is

\(\overrightarrow{\mathbf{v}}_{\mathrm{PG}}=\overrightarrow{\mathbf{v}}_{\mathrm{PA}}+\overrightarrow{\mathbf{v}}_{\mathrm{AG}}\), where \(\mathrm{P}=\) plane, \(\mathrm{A}=\) air, and \(\mathrm{G}=\) ground. From the geometry in Figure, we can solve easily for the magnitude of the velocity of the plane with respect to the ground and the angle of the plane’s heading, \(\theta\).

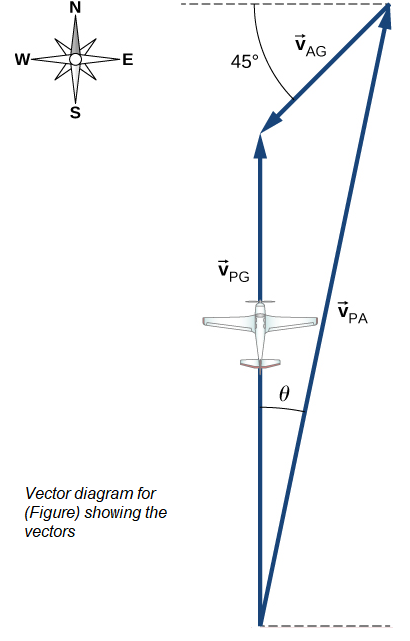
(a) Known quantities:
\(
\begin{array}{l}
\left|\overrightarrow{\mathbf{v}}_{\text {PA }}\right|=300 \mathrm{~km} / \mathrm{h} \\
\left|\overrightarrow{\mathbf{v}}_{\text {AG }}\right|=90 \mathrm{~km} / \mathrm{h}
\end{array}
\)
Substituting into the equation of motion, we obtain \(\left|\overrightarrow{\mathbf{v}}_{\text {PG }}\right|=230 \mathrm{~km} / \mathrm{h}\).
(b) The angle \(\theta=\tan ^{-1} \frac{63.64}{300}=12^{\circ}\) east of north.

Different cases of relative velocity

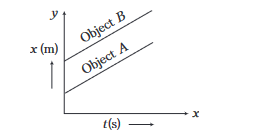
Case I: When the two objects move with equal velocities, i.e. \(v_A=v_B\) or \(v_B-v_A=0\). It means, the two objects stay at constant distance apart during the whole journey. In this case, the position-time graph of two objects are parallel straight lines.

Case II: If both objects \(A\) and \(B\) move along parallel straight lines in the opposite direction, then relative velocity of \(B\) with respect to \(A\) is given as
\(
{v}_{B A}={v}_B-\left(-{v}_A\right)={v}_B+{v}_A
\)
and the relative velocity of \(A\) with respect to \(B\) is given by
\(
{v}_{A B}={v}_A-\left(-{v}_B\right)={v}_A+{v}_B
\)

Case III:

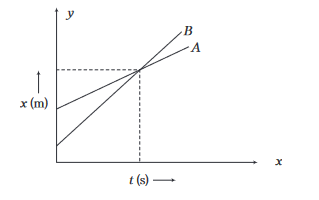
If \(v_A<v_B, v_A-v_B\) is negative.
Then, \(x-x_0<0\)
\(
\Rightarrow \quad x<x_0
\)
where, \(x_0=\) initial displacement of object \(A\) with respect to \(B\)
and \(\quad x=\) displacement of object \(A\) with respect to \(B\) at time \(t\).
i.e. \(\left(x-x_0\right)\) is negative. It means the separation between the two objects will go on decreasing and two objects will meet and object \(B\) will overtake object \(A\) at this time. In this case, relative velocity of \(A\) with respect to \(B\), i.e.
\(
\begin{aligned}
v_{A B} & =v_A-v_B =-v_{B A}
\end{aligned}
\)

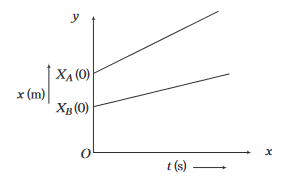
Case IV: If \(v_A>v_B, v_A-v_B\) is positive.
Then, \(x-x_0>0\), i.e. \(\left(x-x_0\right)\) is positive.
It means the separation between the two objects will go on increasing with time, i.e. the separation \(\left(x-x_0\right)\) between them will increase by an amount \(\left(v_A-v_B\right)\) after each unit of time.
Therefore, their position-time graphs will open out gradually as shown below.

Example 12: A man \(A\) moves due east with velocity \(6 \mathrm{~ms}^{-1}\) and another man \(B\) moves in \(N-30^{\circ} \mathrm{E}\) with \(6 \mathrm{~ms}^{-1}\). Find the velocity of \(B\) with respect to \(A\).

Answer: Given,
\(
\begin{aligned}
\mathbf{v}_A & =6 \hat{\mathbf{i}} \\
\mathbf{v}_B & =v_B \cos 60^{\circ} \hat{\mathbf{i}}+v_B \sin 60^{\circ} \hat{\mathbf{j}} \\
& =6\left(\frac{1}{2}\right) \hat{\mathbf{i}}+6\left(\frac{\sqrt{3}}{2}\right) \hat{\mathbf{j}}=3 \hat{\mathbf{i}}+3 \sqrt{3} \hat{\mathbf{j}}
\end{aligned}
\)
To find the velocity,
\(
\begin{aligned}
\mathbf{v}_{B A} & =\mathbf{v}_B-\mathbf{v}_A=(3 \hat{\mathbf{i}}+3 \sqrt{3} \hat{\mathbf{j}})-6 \hat{\mathbf{i}} \\
& =-3 \hat{\mathbf{i}}+3 \sqrt{3} \hat{\mathbf{j}} \\
\left|\mathbf{v}_{B A}\right| & =\sqrt{(-3)^2+(3 \sqrt{3})^2} \\
& =\sqrt{9+27}=\sqrt{36}=6 \mathrm{~ms}^{-1}
\end{aligned}
\)
Here, \(\hat{\mathbf{i}}\) is – ve and \(\hat{\mathbf{j}}\) is + ve. So, second quadrant is possible.
Direction,
\(
\tan \alpha=\frac{\text { coefficient of } \hat{\mathbf{j}}}{\text { coefficient of } \hat{\mathbf{i}}}=\frac{3 \sqrt{3}}{-3}=-\sqrt{3}
\)
\(
\Rightarrow \quad \alpha=-60^{\circ}
\)

Example 13: Car \(A\) has an acceleration of \(2 \mathrm{~m} / \mathrm{s}^2\) due east and car \(B, 4 \mathrm{~m} / \mathrm{s}^2\) due north. What is the acceleration of car \(B\) with respect to car \(A\) ?

Answer: It is a two dimensional motion, therefore
\(
\begin{aligned}
\mathbf{a}_{B A}=\text { acceleration of } & \text { car } B \text { with respect to car } A \\
& =\mathbf{a}_B-\mathbf{a}_A
\end{aligned}
\)

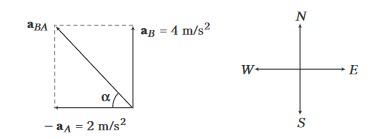
Here, \(\mathbf{a}_B=\) acceleration of car \(B=4 \mathrm{~m} / \mathrm{s}^2\) (due north) and
\(\mathbf{a}_A=\) acceleration of \(\operatorname{car} A=2 \mathrm{~m} / \mathrm{s}^2\) (due east)
\(
\begin{aligned}
\left|\mathbf{a}_{B A}\right| & =\sqrt{(4)^2+(2)^2} \\
& =2 \sqrt{5} \mathrm{~m} / \mathrm{s}^2
\end{aligned}
\)
and
\(
\alpha=\tan ^{-1}\left(\frac{4}{2}\right)=\tan ^{-1}
\)
Thus, \(\mathbf{a}_{B A}\) is \(2 \sqrt{5} \mathrm{~m} / \mathrm{s}^2\) at an angle of \(\alpha=\tan ^{-1}\) (2) from west towards north.

Example 14: A police van moving on a highway with a speed of \(30 \mathrm{kmh}^{-1}\) fires a bullet at a thief car which is speeding away in the same direction with a speed of \(190 \mathrm{kmh}^{-1}\). If the muzzle speed of the bullet is \(150 \mathrm{~ms}^{-1}\), find speed of the bullet with respect to the thief’s car.

Answer: Let \(v_b\) is velocity of bullet, \(v_p\) is velocity of police van and \(v_t\) is velocity of thief’s car. Then, speed of the bullet (Since the bullet is fired from a police moving van) with respect to the thief’s car,
\(
\begin{array}{l}
v_{b p}=v_b-v_p \\
v_b=v_{b p}+v_p=150 \times \frac{18}{5} \mathrm{kmh}^{-1}+30 \mathrm{kmh}^{-1}=570 \mathrm{kmh}^{-1} \\
v_{b t}=v_b-v_t=570 \mathrm{kmh}^{-1}-190 \mathrm{kmh}^{-1}=380 \mathrm{kmh}^{-1}
\end{array}
\)

Example 15: Delhi is at a distance of \(200 \mathrm{~km}\) from Ambala. Car A set out from Ambala at a speed of \(30 \mathrm{kmh}^{-1}\) and car B set out at the same time from Delhi at a speed of \(20 \mathrm{kmh}^{-1}\). When will they meet each other? What is the distance of the meeting point from Ambala?

Answer: 

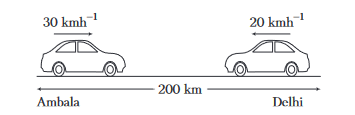
Relative velocity,
\(\begin{aligned} \mathbf{v}_{A B} & =\mathbf{v}_A-\mathbf{v}_B \\ & =30-(-20)=50 \mathrm{kmh}^{-1}\end{aligned}\)
They will meet after time
\(
t=\frac{s}{v_{A B}}=\frac{200}{50}=4 \mathrm{~h}
\)
Distance from Ambala, where they will meet,
\(
x=30 \times 4=120 \mathrm{~km}
\)

Relative velocity of rain

Consider a man walking east with velocity \(\mathbf{v}_m\) represented by \(O A\). Let the rain be falling vertically downwards with velocity \(\mathbf{v}_r\), represented by \(O B\). To find the relative velocity of rain w.r.t. man (i.e. \(\mathbf{v}_{r m}\) ) being the man at rest by imposing a velocity \(-\mathbf{v}_m\) on man and apply this velocity on rain also. So, the man should hold his umbrella in the direction of \(\mathbf{v}_m\) or \(\mathbf{v}_r-\mathbf{v}_m\), to save him from rain.
Now, the relative velocity of rain w.r.t. man will be the resultant velocity of \(\mathbf{v}_r(=O B)\) and \(-\mathbf{v}_m(=O A)\), which will be represented by diagonal \(O C\) of rectangle \(O A C B\).
\(
\mathbf{v}_{r m}=\sqrt{v_r^2+v_m^2+2 v_r v_m \cos 90^{\circ}}=\sqrt{v_r^2+v_m^2}
\)

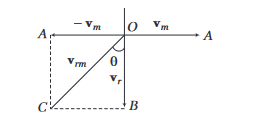
If \(\theta\) is the angle which \(\mathbf{v}_{r m}\) makes with the vertical direction, then
\(
\tan \theta=\frac{B C}{O B}=\frac{\mathbf{v}_m}{\mathbf{v}_r} \text { or } \theta=\tan ^{-1}\left(\frac{\mathbf{v}_m}{\mathbf{v}_r}\right)
\)
Here, angle \(\theta\) is from vertical towards west and is written as \(\theta\), west of vertical.

Note: In the above problem, if the man wants to protect himself from the rain, he should hold his umbrella in the direction of relative velocity of rain w.r.t. man, i.e. the umbrella should be held making an angle \(\theta\) from west of vertical.

Example 16: To a man walking at the rate of \(3 \mathrm{~km} / \mathrm{h}\), the rain appears to fall vertically. When he increases his speed to \(6 \mathrm{~km} / \mathrm{h}\), it appears to meet him at an angle of \(45^{\circ}\) with vertical. Find the speed of rain.

Answer: Let \(\hat{\mathbf{i}}\) and \(\hat{\mathbf{j}}\) be the unit vectors in horizontal and vertical directions, respectively.
Let velocity of rain,
\(
\mathbf{v}_r=a \hat{\mathbf{i}}+b \hat{\mathbf{j}} \dots(i)
\)
Then, speed of rain will be
\(
\left|\mathbf{v}_r\right|=\sqrt{a^2+b^2} \dots(ii)
\)
In the first case, \(\mathbf{v}_m=\) velocity of man \(=3 \hat{\mathbf{i}}\)
\(
\therefore \quad \mathbf{v}_{r m}=\mathbf{v}_r-\mathbf{v}=(a-3) \hat{\mathbf{i}}+b \hat{\mathbf{j}}
\)
Since rain is in vertical direction (\(x\) components will be 0). Hence,
\(
a-3=0 \text { or } a=3
\)
In the second case \(\mathbf{v}_{m}=6 \hat{\mathbf{i}}\)
\(
\therefore \quad \mathbf{v}_{r m}=(a-6) \hat{\mathbf{i}}+b \hat{\mathbf{j}}=-3 \hat{\mathbf{i}}+b \hat{\mathbf{j}}
\)
This seems to be at \(45^{\circ}\) with vertical. Hence, \(|b|=3\)
Therefore, from Eq. (ii), speed of rain is
\(
\left|\mathbf{v}_r\right|=\sqrt{(3)^2+(3)^2}=3 \sqrt{2} \mathrm{~km} / \mathrm{h}
\)

Example 17: A man is walking with \(3 \mathrm{~m} / \mathrm{s}\), due east. Rain is falling vertically downwards with speed \(4 \mathrm{~m} / \mathrm{s}\). Find the direction in which man should hold his umbrella, so that rain does not wet him.

Answer: As we discussed above, he should hold his umbrella in the direction of \(\mathbf{v}_{r m}\) or \(\mathbf{v}_r-\mathbf{v}_m\)

\(
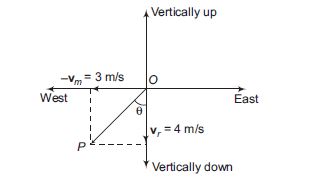
\begin{aligned}
\mathrm{OP} & =\mathbf{v}_r+\left(-\mathbf{v}_m\right)=\mathbf{v}_r-\mathbf{v}_m=\mathbf{v}_{r m} \\
\tan \theta & =\frac{3}{4} \\
\theta & =\tan ^{-1}\left(\frac{3}{4}\right)=37^{\circ}
\end{aligned}
\)

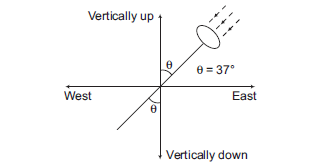
Therefore, man should hold his umbrella at an angle of \(37^{\circ}\) east of vertical (or \(37^{\circ}\) from vertical towards east).

Crossing the River (River-Boat Problems)

In river-boat problems, we come across the following three terms :

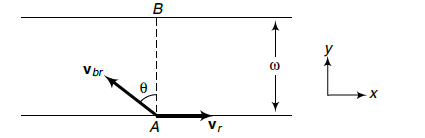
\(\mathbf{v}_r=\) absolute velocity of river
\(\mathbf{v}_{b r}=\) velocity of boatman with respect to river or velocity of boatman in still water and \(\mathbf{v}_b=\) absolute velocity of boatman.
Here, it is important to note that \(\mathbf{v}_{b r}\) is the velocity of boatman with which he steers and \(\mathbf{v}_b\) is the actual velocity of boatman relative to ground.
Further,
\(
\mathbf{v}_b=\mathbf{v}_{b r}+\mathbf{v}_r
\)
\(
\left(\text { as } \mathbf{v}_{b r}=\mathbf{v}_b-\mathbf{v}_r\right)
\)
Now, let us derive some standard results and their special cases.
A boatman starts from point \(A\) on one bank of a river with velocity \(\mathbf{v}_{b r}\) in the direction shown in figure above. River is flowing along positive \(x\)-direction with velocity \(\mathbf{v}_r\). Width of the river is \(\omega\), then
Therefore,
\(
\begin{aligned}
\mathbf{v}_b & =\mathbf{v}_r+\mathbf{v}_{b r} \\
v_{b x} & =v_{r x}+v_{b r x}=v_r-v_{b r} \sin \theta \\
v_{b y} & =v_{r y}+v_{b r y} \\
& =0+v_{b r} \cos \theta=v_{b r} \cos \theta
\end{aligned}
\)
Now, time taken by the boatman to cross the river is
\(
t=\frac{\omega}{v_{b y}}=\frac{\omega}{v_{b r} \cos \theta} \quad \text { or } \quad t=\frac{\omega}{v_{b r} \cos \theta} \dots(i)
\)
Further, displacement along \(x\)-axis when he reaches the other bank (also called drift) is
\(
\begin{array}{c}
x=v_{b x} t=\left(v_r-v_{b r} \sin \theta\right) \frac{\omega}{v_{b r} \cos \theta} \\
x=\left(v_r-v_{b r} \sin \theta\right) \frac{\omega}{v_{b r} \cos \theta} \dots(ii)
\end{array}
\)

Let’s discuss the three special cases:

Case-I: Condition when the boatman crosses the river in shortest interval of time

From Eq. (i) we can see that time \((t)\) will be minimum when \(\theta=0^{\circ}\), i.e. the boatman should steer his boat perpendicular to the river current. To cross the river in possible shortest time the boatman should go along \(A B\) as shown below.

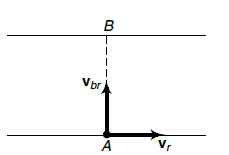
Also,
\(
t_{\text {min }}=\frac{\omega}{v_{b r}}
\)
as
\(
\cos \theta=1
\)

Case-II: Condition when the boatman wants to reach point B, i.e. at a point just opposite from where he started

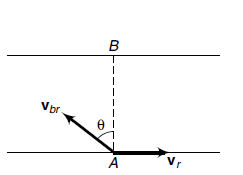
In this case, the drift (\(x\)) should be zero.
\(\therefore \quad x=0\)
\(
\begin{array}{l}
\left(v_r-v_{b r} \sin \theta\right) \frac{\omega}{v_{b r} \cos \theta}=0 \\
v_r=v_{b r} \sin \theta \\
\sin \theta=\frac{v_r}{v_{b r}} \quad \text { or } \quad \theta=\sin ^{-1}\left(\frac{v_r}{v_{b r}}\right)
\end{array}
\)
Hence, to reach point \(B\) the boatman should row at an angle \(\theta=\sin ^{-1}\left(\frac{v_r}{v_{b r}}\right)\) upstream from \(A B\).
Further, since \(\sin \theta\) can’t be greater than 1.
So, if \(v_r \geq v_{b r}\), the boatman can never reach at point \(B\). Because if \(v_r=v_{b r}, \sin \theta=1\) or \(\theta=90^{\circ}\) and it is just impossible to reach at \(B\) if \(\theta=90^{\circ}\). Moreover, it can be seen that \(v_b=0\) if \(v_r=v_{b r}\) and \(\theta=90^{\circ}\). Similarly, if \(v_r>v_{b r}, \sin \theta>1\), i.e. no such angle exists. Practically, it can be realized in this manner that it is not possible to reach at \(B\) if river velocity \(\left(v_r\right)\) is too high.

Note: In a general case, resolve \(\mathbf{v}_{b r}\) along the river and perpendicular to river as shown below.

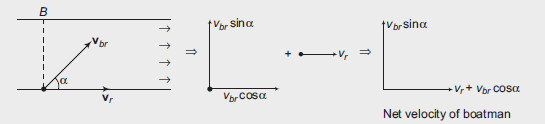
Now, the boatman will cross the river with component of \(\mathbf{v}_{b r}\) perpendicular to river ( \(=v_{b r} \sin \alpha\) in above case)
\(
\therefore \quad t=\frac{\omega}{v_{b r} \sin \alpha}
\)
To cross the river in minimum time, why to take help of component of \(\mathbf{v}_{b r}\) (which is always less that \(v_{b r}\) ), the complete vector \(\mathbf{v}_{b r}\) should be kept perpendicular to the river current. Due to the other component \(v_r+v_{b r} \cos \alpha\), boatman will drift along the river by a distance \(x=\left(v_r+v_{b r} \cos \alpha\right)\) (time)
To reach a point \(B\), which is just opposite to the starting point \(A\), net velocity of boatman \(\mathbf{v}_b\) or the vector sum of \(\mathbf{v}_r\) and \(\mathbf{v}_{b r}\) should be along \(A B\). The velocity diagram is as under

From the diagram we can see that,
\(
\left|\mathbf{v}_b\right| \text { or } v_b=\sqrt{v_{b r}^2-v_r^2} \dots(i)
\)
Time, \(t=\frac{\omega}{v_b}=\frac{\omega}{\sqrt{v_{b r}^2-v_r^2}}\)
drift \(x=0\) and \(\sin \theta=\frac{v_r}{v_{b r}}\) or \(\theta=\sin ^{-1}\left(\frac{v_r}{v_{b r}}\right)\)
From Eq. (i), we can see that this case is possible if,
\(
v_{b r}>v_r
\)
otherwise, \(v_b\) is either zero or imaginary.
If the boatman rows his boat along the river (downstream), then net velocity of boatman will be \(v_{b r}+v_r\).
If he rows along the river upstream then net velocity of boatman will be \(v_{b r} \sim v_r\).

Derivation of equation(i):

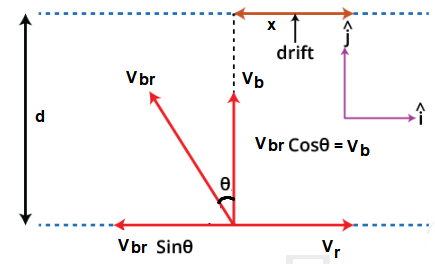
For the boat to go across the river along the shortest path, the drift \(x\) should be minimum or more precisely zero. The drift \(\mathrm{x}\) will be zero when the velocity in the \(\hat{\mathbf{i}}\) direction will be zero. This means that
\(
v_r-v_{br} \sin \theta=0
\)
\(
v_{br} \sin \theta=v_r
\)
\(
\sin \theta=\frac{v_r}{v_{br}}
\)
\(
\theta=\sin ^{-1}\left(\frac{v_r}{v_{br}}\right)
\)
So in order for the boat to go along the shortest path it has to go at an angle of \(\theta=\sin ^{-1}\left(\frac{v_r}{v_{br}}\right)\) with the vertical.
The time for the shortest path will be given as
\(
t=\frac{\omega}{v_b}=\frac{d}{v_b}=\frac{d}{v_{br} \cos \theta}
\)
Now we have \(\sin \theta=\frac{v_r}{v_{br}}\) and we know that
\(
\sin ^2 \theta+\cos ^2 \theta=1
\)
\(
\cos ^2 \theta=1-\sin ^2 \theta
\)
\(
\cos \theta=\sqrt{1-\sin ^2 \theta}
\)
Putting the value of \(\sin \theta\) will give
\(
\begin{array}{l}
\cos \theta=\sqrt{1-\left(\frac{v_r}{v_{br}}\right)^2} \\
\cos \theta=\sqrt{1-\frac{v_r^2}{v_{br}^2}} \\
\cos \theta=\sqrt{\frac{v_{br}^2-v_r^2}{v_{br}^2}}
\end{array}
\)
Inserting this in the expression for time gives
\(
\begin{array}{l}
t=\frac{d}{v_{\text {br }} \cos \theta}=\frac{d}{v_{br}\left(\frac{\sqrt{v_{br}^2-v_r^2}}{v_{br}}\right)} \\
t=\frac{d}{\sqrt{v_{br}^2-v_r^2}}=\frac{d}{v_b}
\end{array}
\)
\(
\left|\mathbf{v}_b\right| \text { or } v_b=\sqrt{v_{b r}^2-v_r^2}
\)
This is the time taken along the shortest path.

Example 18: Width of a river is \(30 \mathrm{~m}\), river velocity is \(2 \mathrm{~m} / \mathrm{s}\) and rowing velocity is \(5 \mathrm{~m} / \mathrm{s}\) at \(37^{\circ}\) from the direction of river current (a) find the time taken to cross the river, (b) drift of the boatman while reaching the other shore.

Answer: 

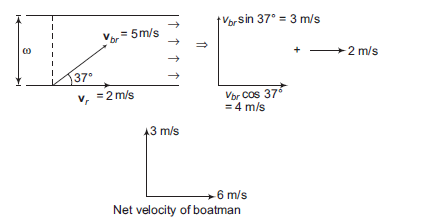
(a) Time taken to cross the river,
\(
t=\frac{\omega}{3}=\frac{30}{3}=10 \mathrm{~s}
\)
(b) Drift along the river
\(
x=(6)(t)=6 \times 10=60 \mathrm{~m}
\)

Example 19: Width of a river is \(30 \mathrm{~m}\), river velocity is \(4 \mathrm{~m} / \mathrm{s}\) and rowing velocity of boatman is \(5 \mathrm{~m} / \mathrm{s}\)
(a) Make the velocity diagram for crossing the river in shortest time. Then, find this shortest time, net velocity of boatman and drift along the river.
(b) Can the boatman reach a point just opposite on the other shore? If yes then make the velocity diagram, the direction in which he should row his boat and the time taken to cross the river in this case.
(c) How long will it take him to row \(10 \mathrm{~m}\) up the stream and then back to his starting point?

Answer: (a) Shortest time

\(
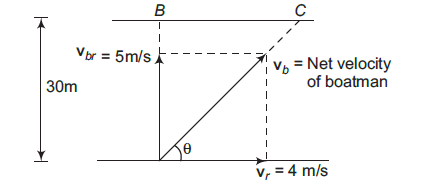
t=\frac{30}{5}=6 \mathrm{~s}=t_{\min }
\)
\(
\left|\mathbf{v}_b\right| = v_b=\sqrt{(5)^2+(4)^2}=\sqrt{41} \mathrm{~m} / \mathrm{s}
\)
\(
\tan \theta=\frac{5}{4} \Rightarrow \theta=\tan ^{-1}\left(\frac{5}{4}\right)
\)
\(
\begin{aligned}
\text { Drift } & =B C=(4)(t)=4 \times 6=24 \mathrm{~m}
\end{aligned}
\)

(b) Since, \(v_{b r}>v_r\), this case is possible. Velocity diagram is as under.

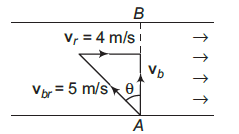
Net velocity \(\left|\mathbf{v}_b\right|\) or \(v_b=\sqrt{(5)^2-(4)^2}=3 \mathrm{~m} / \mathrm{s}\) along \(A B\)
\(
\begin{aligned}
\sin \theta & =\frac{4}{5} \Rightarrow \theta=\sin ^{-1} \frac{4}{5}=53^{\circ} \\
t & =\frac{A B}{v_b}=\frac{30}{3}=10 \mathrm{sec} 
\end{aligned}
\)

Note: If the boatman wants to return to the same point \(A\), then diagram is as under

\(
t_{B A}=\frac{B A}{3}=\frac{30}{3}=10 \mathrm{~s}
\)

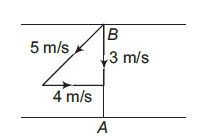
(c)

\(
\begin{aligned}
t=t_{A B}+t_{B A} & =\frac{A B}{v_{b r}-v_r}+\frac{B A}{v_{b r}+v_r} \\
t & =\frac{10}{5-4}+\frac{10}{5+4} \\
& =\frac{100}{9} \mathrm{~s}
\end{aligned}
\)

Example 20: A man crosses a river in a boat. If he cross the river in minimum time, he takes 10 min with a drift \(120 \mathrm{~m}\). If he crosses the river taking shortest path, he takes \(12.5 \mathrm{~min}\), find
(i) width of the river,
(ii) velocity of the boat with respect to water
(iii) and speed of the current.

Answer: Let \(v_r=\) velocity of river, \(v_{b r}=\) velocity of boat in still water and \(w=\) width of river.
Given, \(t_{\min }=10 \mathrm{~min}\) or \(\frac{w}{v_{b r}}=10 \dots(i)\)
Drift in this case will be
\(
\begin{aligned}
x & =v_r t \\
\therefore \quad 120 & =10 v_r \dots(ii)
\end{aligned}
\)
Shortest path is taken when \(v_b\) is along \(A B\). In this case,
\(
v_b=\sqrt{v_{b r}^2-v_r^2}
\)
Now, \(12.5=\frac{w}{v_b}=\frac{w}{\sqrt{v_{b r}^2-v_r^2}} \dots(iii)\)
Solving these three equations, we get \(v_{b r}=20 \mathrm{~m} / \mathrm{min}, v_r=12 \mathrm{~m} / \mathrm{min}\) and \(w=200 \mathrm{~m}\)

Example 21: A man wants to reach point B on the opposite bank of a river flowing at a speed \(u\) as shown in figure. What minimum speed relative to water should the man have, so that he can reach point B ? In which direction should he swim?

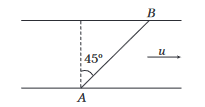
Answer: Let \(v\) be the speed of boatman in still water.

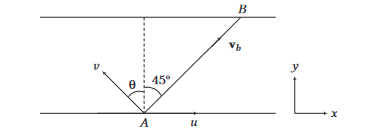
Resultant of \(v\) and \(u\) should be along \(A B\). Components of \(\mathbf{v}_b\) (absolute velocity of boatman) along \(x\) and \(y\)-directions are
\(
v_x=u-v \sin \theta \text { and } v_y=v \cos \theta
\)
Further, \(\tan 45^{\circ}=\frac{v_y}{v_x}\)
\(
\begin{aligned}
\text { or } & 1 =\frac{v \cos \theta}{u-v \sin \theta} \\
\therefore & v =\frac{u}{\sin \theta+\cos \theta}=\frac{u}{\sqrt{2} \sin \left(\theta+45^{\circ}\right)}
\end{aligned}
\)
\(v\) is minimum, at
\(
\begin{aligned}
\theta+45^{\circ} & =90^{\circ} \\
\theta & =45^{\circ}
\end{aligned}
\)
and
\(
v_{\min }=\frac{u}{\sqrt{2}}
\)

Example 22: A man can row a boat with \(4 \mathrm{~km} / \mathrm{h}\) in still water. If he is crossing a river, where the current is \(2 \mathrm{~km} / \mathrm{h}\).
(i) In what direction will his boat be headed, if he wants to reach a point on the other bank, directly opposite to starting point?
(ii) If width of the river is \(4 \mathrm{~km}\), how long will the man take to cross the river, with the condition in part (i)?
(iii) In what direction should he head the boat, if he wants to cross the river in shortest time and what is this minimum time?
(iv) How long will it take him to row \(2 \mathrm{~km}\) up the stream and then back to his starting point?

Answer: (i) Given, \(v_{b r}=4 \mathrm{~km} / \mathrm{h}\) and \(v_r=2 \mathrm{~km} / \mathrm{h}\)
\(
\begin{aligned}
\therefore \quad \theta & =\sin ^{-1}\left(\frac{v_r}{v_{b r}}\right) \\
& =\sin ^{-1}\left(\frac{2}{4}\right) \\
& =\sin ^{-1}\left(\frac{1}{2}\right)=30^{\circ}
\end{aligned}
\)
Hence, to reach the point directly opposite to starting point he should head the boat at an angle of \(30^{\circ}\) with \(A B\) or \(90^{\circ}+30^{\circ}=120^{\circ}\) with the river flow.
(ii) Time taken by the boatman to cross the river,
\(
\begin{aligned}
w & =\text { width of river }=4 \mathrm{~km} \\
v_{b r} & =4 \mathrm{~km} / \mathrm{h} \\
\text { and } \quad \theta & =30^{\circ}
\end{aligned}
\)
\(
\therefore \quad t=\frac{4}{4 \cos 30^{\circ}}=\frac{2}{\sqrt{3}} \mathrm{~h}
\)
(iii) For shortest time \(\theta=0^{\circ}\) and \(\quad t_{\text {min }}=\frac{w}{v_{b r} \cos 0^{\circ}}=\frac{4}{4}=1 \mathrm{~h}\)
Hence, he should head his boat perpendicular to the river current for crossing the river in shortest time and this shortest time is \(1 \mathrm{~h}\).
\(
\text { (iv) } t=t_{C D}+t_{D C}
\)

\(
\begin{aligned}
t & =\frac{C D}{v_{b r}-v_r}+\frac{D C}{v_{b r}+v_r} \\
& =\frac{2}{4-2}+\frac{2}{4+2}=1+\frac{1}{3}=\frac{4}{3} \mathrm{~h}
\end{aligned}
\)

Example 23: A boat moves relative to water with a velocity \(v\) is \(n\) times less than the river flow \(u\). At what angle to the stream direction must the boat move to minimise drifting?

Answer: In this problem, one thing should be carefully noted that the velocity of boat is less than the river flow velocity. Hence, boat cannot reach the point directly opposite to its starting point, i.e. drift can never be zero. Suppose boat starts at an angle $\theta$ from the normal direction up stream as shown.

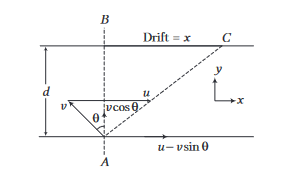
Component of velocity of boat along the river,
\(
v_x=u-v \sin \theta
\)
and velocity perpendicular to the river,
\(
v_y=v \cos \theta
\)
Time taken to cross the river is
\(
t=\frac{d}{v_y}=\frac{d}{v \cos \theta}
\)
Drift \(x=\left(v_x\right) t=(u-v \sin \theta) \frac{d}{v \cos \theta}\)
\(
=\frac{u d}{v} \sec \theta-d \tan \theta
\)
The drift \(x\) is minimum when \(\frac{d x}{d \theta}=0\)
or \(\left(\frac{u d}{v}\right)(\sec \theta \cdot \tan \theta)-d \sec ^2 \theta=0\)
\(
\frac{u}{v} \sin \theta=1 \Rightarrow \sin \theta=\frac{v}{u}
\)
So, for minimum drift, the boat must move at an angle
\(
\theta=\sin ^{-1}\left(\frac{v}{u}\right)=\sin ^{-1}\left(\frac{1}{n}\right)
\)
from normal direction.

Example 24: A boat with a speed of \(10 \mathrm{~m} / \mathrm{s}\) relative to the water leaves the south bank in the direction of \(37^{\circ}\) west of north. The river is \(300\mathrm{~m}\)-wide and flows due east at a speed of \(2 \mathrm{~m} / \mathrm{s}\). What are the
(a) magnitude and
(b) direction of the boat’s velocity relative to the ground?
(c) How long does the boat take to reach the other side of the river?

Answer: This type of relative motion problem in two dimensions requires some information about resolving vectors into unit vectors along the \(x\) and \(y\) axes.
Sketching a vector diagram and applying the tip-to-tail vector sum rule to find the unknown velocity is not always the right method.
In this question, we see that the two velocities are not perpendicular to each other, so the triangle that is made is not a right triangle and correspondingly, we cannot use the Pythagorean theorem or angle formula to find its magnitude and direction.
When the given velocities were perpendicular to each there, then we could use the following well-known vector addition equation
\(
\vec{v}_{B G}=\vec{v}_{B W}+\vec{v}_{W G}
\)
Here, we clearly see that the two given velocities are not perpendicular, so the vector diagram is not a useful way and it is better to apply the method of vector addition by vector components.

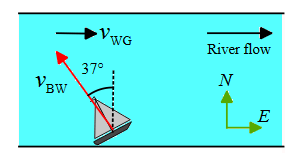
We are given the following information: the Boat’s speed relative to the Water, i.e., \(v_{B W}=10 \mathrm{~m} / \mathrm{s}\), the speed of Water with respect to the Ground, i.e., \(v_{W G}=2 \mathrm{~m} / \mathrm{s}\). As you can see in the figure below, \(\vec{v}_{B W}\) is resolved along the \(x\) and \(y\) axes as
\(
\vec{v}_{B W}=10 \sin 37^{\circ}(-\hat{i})+10 \cos 37^{\circ} \hat{j}
\)

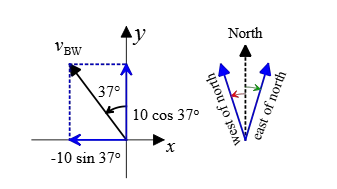
The water flows also due east or the positive \(x\)-direction, i.e., \(\vec{v}_{W G}=2(\hat{i}) \mathrm{m} / \mathrm{s}\).
The combined velocities give us the components of the Boat’s velocity relative to the Ground
\(
\begin{array}{c}
\vec{v}_{B G}=\vec{v}_{B W}+\vec{v}_{W G} \\
=\left(10 \sin 37^{\circ}(-\hat{i})+10 \cos 37^{\circ} \hat{j}\right)+2 \hat{i} \\
=\left(-10 \sin 37^{\circ}+2\right) \hat{i}+10 \cos 37^{\circ} \hat{j} \\
=-4 \hat{i}+8 \hat{j}
\end{array}
\)
Now, given this we can simply find the direction that this vector makes with the standard direction as measured counterclockwise from the positive \(x\)-direction by the following formula
\(
\begin{aligned}
\alpha & =\arctan \left(\frac{v_y}{v_x}\right) \\
& =\arctan \left(\frac{8}{-4}\right) \\
& =-63^{\circ}
\end{aligned}
\)
But the story is not over yet! Whenever a vector is in the second or third quadrant, the angle obtained by the above formula must be subtracted from the \(180^{\circ}\) to give the true angle measured counterclockwise from the \(+x\)-direction.

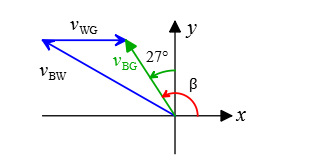
In this case, \(\vec{v}_{B G}\) lies in the second quadrant. Therefore, the correct angle is
\(
\beta=180^{\circ}-63^{\circ}=117^{\circ}
\)
If this angle is subtracted from \(90^{\circ}\), then we can find its direction relative to the north direction. In this case, the boat’s velocity relative to the ground heads \(27^{\circ}\) west of north, as illustrated in the figure.

Minimum distance between two bodies in motion

When two bodies are in motion, the questions like, the minimum distance between them or the time when one body overtakes the other can be solved easily by the principle of relative motion. In these type of problems one body is assumed to be at rest and the relative motion of the other body is considered. By assuming so two body problem is converted into one body problem and the solution becomes easy. Following example will illustrate the statement.

Example 25: Car A and car B start moving simultaneously in the same direction along the line joining them. Car A moves with a constant acceleration \(a=4 \mathrm{~ms}^{-2}\), while car \(B\) moves with a constant velocity \(v=1 \mathrm{~ms}^{-1}\). At time \(t=0\), car \(A\) is \(10 \mathrm{~m}\) behind car \(B\). Find the time when car \(A\) overtakes car \(B\).

Answer: Given, \(u_A=0, u_B=1 \mathrm{~ms}^{-1}, a_A=4 \mathrm{~ms}^{-2}\) and \(a_B=0\) Assuming car \(B\) to be at rest, we get
\(
\begin{array}{c}
u_{A B}=u_A-u_B=0-1=-1 \mathrm{~ms}^{-1} \\
a_{A B}=a_A-a_B=4-0=4 \mathrm{~ms}^{-2}
\end{array}
\)
Now, the problem can be assumed in simplified form as follows

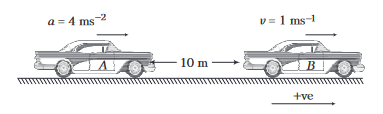
Substituting the proper values in equation
\(
\begin{aligned}
s & =u t+\frac{1}{2} a t^2 \text {, we get } \\
10 & =-t+\frac{1}{2}(4)\left(t^2\right) \\
\text { or } \quad 2 t^2-t-10 & =0
\end{aligned}
\)

or \(\quad t=\frac{1 \pm \sqrt{1+80}}{4}=\frac{1 \pm \sqrt{81}}{4}=\frac{1 \pm 9}{4}\)
or \(\quad t=2.5 \mathrm{~s}\) and \(-2 \mathrm{~s}\)
Ignoring the negative value, the desired time is \(2.5 \mathrm{~s}\).

Note: The above problem can also be solved without using the concept of relative motion as follows
At the time, when \(A\) overtakes \(B, s_A=s_B+10\)
\(\therefore \quad \frac{1}{2} \times 4 \times t^2=1 \times t+10\)
or \(2 t^2-t-10=0\)
which on solving gives \(t=2.5 \mathrm{~s}\) and \(-2 \mathrm{~s}\), the same as we found above.
As per my opinion, this approach (by taking absolute values) is more suitable in case of two body problem in one dimensional motion. Let us see one more example in support of it.

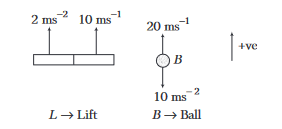
Example 26: An open lift is moving upwards with velocity \(10 \mathrm{~ms}^{-1}\). It has an upward acceleration of \(2 \mathrm{~ms}^{-2}\). \(A\) ball is projected upwards with velocity \(20 \mathrm{~ms}^{-1}\) relative to ground. Find
(i) time when ball again meets the lift,
(ii) displacement of lift and ball at that instant
(iii) and distance travelled by the ball upto that instant.
(Take, \(g=10 \mathrm{~ms}^{-2}\) )

Answer: (i) At the time, when ball again meets the lift, \(s_L=s_B\)
\(
\therefore \quad 10 t+\frac{1}{2} \times 2 \times t^2=20 t-\frac{1}{2} \times 10 t^2
\)

Solving this equation, we get
\(
t=0 \text { and } t=\frac{5}{3} \mathrm{~s}
\)
\(\therefore\) Ball will again meet the lift after \(\frac{5}{3} \mathrm{~s}\).
(ii) At this instant, \(s_L=s_B=10 \times \frac{5}{3}+\frac{1}{2} \times 2 \times\left(\frac{5}{3}\right)^2\)
\(
=\frac{175}{9} \mathrm{~m}=19.4 \mathrm{~m}
\)
(iii) For the ball \(u \uparrow \downarrow a\). Therefore, we will first find \(t_0\), the time when its velocity becomes zero.
\(
t_0=\left|\frac{u}{a}\right|=\frac{20}{10}=2 \mathrm{~s}
\)
As \(t\left(=\frac{5}{3} s\right)<t_0\), distance and displacement are equal or
\(
d=19.4 \mathrm{~m}
\)

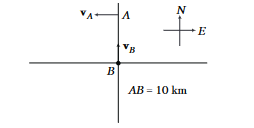
Example 27: Two ships \(A\) and \(B\) are \(10 \mathrm{~km}\) apart on a line running south to north. Ship \(A\) farther north is streaming west at \(20 \mathrm{kmh}^{-1}\) and ship B is streaming north at \(20 \mathrm{kmh}^{-1}\). What is their distance of closest approach and how long do they take to reach it?

Answer: Ships \(A\) and \(B\) are moving with same speed \(20 \mathrm{kmh}^{-1}\) in the directions as shown in figure. It is a two dimensional, two body problem with zero acceleration. Let us find \(\mathbf{v}_{B A}\).

\(
\begin{array}{rlrl}
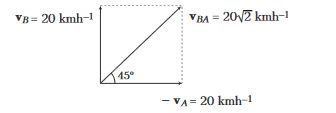
\mathbf{v}_{B A} & =\mathbf{v}_B-\mathbf{v}_A \\
\text { Here, } \quad & \left|\mathbf{v}_{B A}\right| =\sqrt{(20)^2+(20)^2}=20 \sqrt{2} \mathrm{kmh}^{-1}
\end{array}
\)
i.e. \(v_{B A}\) is \(20 \sqrt{2} \mathrm{kmh}^{-1}\) at an angle of \(45^{\circ}\) from east towards north. Thus, the given problem can be simplified as

\(A\) is at rest and \(B\) is moving with \(\mathbf{v}_{B A}\) in the direction as shown in figure. Therefore, the minimum distance between the two is
\(
s_{\min }=A C=A B \sin 45^{\circ}=10\left(\frac{1}{\sqrt{2}}\right) \mathrm{km}=5 \sqrt{2} \mathrm{~km}
\)

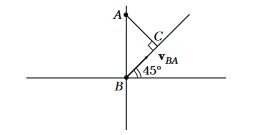
and the desired time is
\(
\begin{aligned}
t & =\frac{B C}{\left|\mathbf{v}_{B A}\right|}=\frac{5 \sqrt{2}}{20 \sqrt{2}} \quad(\because B C=A C=5 \sqrt{2} \mathrm{~km}) \\
& =\frac{1}{4} \mathrm{~h}=15 \mathrm{~min}
\end{aligned}
\)

Aircraft Wind Problems

This is similar to river boat problems. The only difference is that \(\mathbf{v}_{b r}\) is replaced by \(\mathbf{v}_{a w}\) (velocity of aircraft with respect to wind or velocity of aircraft in still air), \(\mathbf{v}_r\) is replaced by \(\mathbf{v}_w\) (velocity of wind) and \(\mathbf{v}_b\) is replaced by \(\mathbf{v}_a\) (absolute velocity of aircraft). Further, \(\mathbf{v}_a=\mathbf{v}_{a w}+\mathbf{v}_w\).

In this case, problem is slightly different. The given variables are

• Complete wind velocity \(\mathbf{v}_w\)
• Steering speed or \(\left|\mathbf{v}_{a w}\right|\)
• Starting point (say \(A\) ) and destination point (say \(B\) )

We have to find direction of \(\mathbf{v}_{a w}\) (or steering velocity) and the time taken in moving from \(A\) to \(B\). The concepts is : net velocity of aircraft \(\mathbf{v}_a\) or vector sum of \(\mathbf{v}_w\) and \(\mathbf{v}_{a w}\) should be along \(A B\).

To solve such problems, we can apply the following steps :

• Take starting point \(A\) as the origin.
• Wind velocity vector is completely given. So, draw \(\mathbf{v}_w\) from point \(A\).
• Draw another vector \(\mathbf{v}_a\) starting from \(A\) in a direction from \(A\) to \(B\).
• In above two steps we have already made two sides of a triangle in vector form. Complete the third side. This represents \(\mathbf{v}_{a w}\). While completing the triangle for finding direction of \(\mathbf{v}_{a w}\), polygon law of vector addition is to be followed, so that,
  \(
  \mathbf{v}_w+\mathbf{v}_{a w}=\mathbf{v}_a
  \)
• Applying, sine law in this triangle, we can find direction of \(\mathbf{v}_{a w}\) and the net velocity of aircraft \(\mathbf{v}_a\). Now,
  time taken, \(\quad t=\frac{A B}{\left|\mathbf{v}_a\right|}\) or \(\frac{A B}{v_a}\)
  The following example will illustrate the above theory:

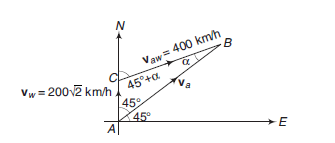
Example 28: An aircraft flies at \(400 \mathrm{~km} / \mathrm{h}\) in still air. A wind of \(200 \sqrt{2} \mathrm{~km} / \mathrm{h}\) is blowing from the south towards north. The pilot wishes to travel from A to a point B north east of \(A\). Find the direction he must steer and time of his journey if \(A B=1000 \mathrm{~km}\).

Answer: Given that \(\quad v_w=200 \sqrt{2} \mathrm{~km} / \mathrm{h}\) \(v_{a w}=400 \mathrm{~km} / \mathrm{h}\) and \(\mathbf{v}_a\) should be along \(A B\) or in north-east direction. Thus, the direction of \(\mathbf{v}_{a w}\) should be such as the resultant of \(\mathbf{v}_w\) and \(\mathbf{v}_{a w}\) is along \(A B\) or in north-east direction.
Let \(\mathbf{v}_{a w}\) makes an angle \(\alpha\) with \(A B\) as shown in Figure below. Applying sine law in triangle \(A B C\), we get
\(
\begin{aligned}
\frac{C B}{\sin 45^{\circ}} & =\frac{A C}{\sin \alpha} \\
\sin \alpha & =\left(\frac{A C}{C B}\right) \sin 45^{\circ}
\end{aligned}
\)

\(
\begin{aligned}
& =\left(\frac{200 \sqrt{2}}{400}\right) \frac{1}{\sqrt{2}}=\frac{1}{2} \\
\alpha & =30^{\circ}
\end{aligned}
\)
\(
\therefore \quad \alpha=30^{\circ}
\)
Therefore, the pilot should steer in a direction at an angle of \(\left(45^{\circ}+\alpha\right)\) or \(75^{\circ}\) from north towards east.
Further, \(\frac{\left|\mathbf{v}_a\right|}{\sin \left(180^{\circ}-45^{\circ}-30^{\circ}\right)}=\frac{400}{\sin 45^{\circ}}\)
\(
\begin{aligned}
\left|\mathbf{v}_a\right| & =\frac{\sin 105^{\circ}}{\sin 45^{\circ}} \times(400) \mathrm{km} / \mathrm{h} \\
& =\left(\frac{\cos 15^{\circ}}{\sin 45^{\circ}}\right)(400) \mathrm{km} / \mathrm{h} \\
& =\left(\frac{0.9659}{0.707}\right)(400) \mathrm{km} / \mathrm{h} \\
& =546.47 \mathrm{~km} / \mathrm{h}
\end{aligned}
\)
\(\therefore\) The time of journey from \(A\) to \(B\) is
\(
\begin{array}{l}
t=\frac{A B}{\left|\mathbf{v}_a\right|}=\frac{1000}{546.47} \mathrm{~h} \\
t=1.83 \mathrm{~h}
\end{array}
\)

Example 29: An aeroplane has to go from a point \(O\) to another point \(A\), at distance d due \(37^{\circ}\) east of north. \(A\) wind is blowing due north at a speed of \(10 \mathrm{~ms}^{-1}\). Find the air speed of the plane is \(v\),
(i) the direction in which the pilot should head the plane to reach the point A
(ii) and the time taken by the plane to go from \(O\) to \(A\).

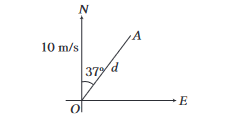
Answer: (i) If a particle moves in a straight line, the velocity of particle perpendicular to straight line should be zero. If an aeroplane moves along \(O A\), the pilot should head the plane towards right of line \(O A\).

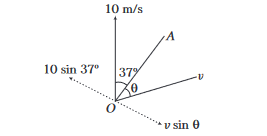
Perpendicular to line \(O A\),
\(
\begin{aligned}
v \sin \theta & =10 \sin 37^{\circ}=6 \\
\sin \theta & =\frac{6}{v} \Rightarrow \theta=\sin ^{-1}\left(\frac{6}{v}\right)
\end{aligned}
\)
The pilot should head the plane at an angle
\(
\sin ^{-1}\left(\frac{6}{v}\right) \text { east of line } O A
\)

(ii) Along line \(O A\)

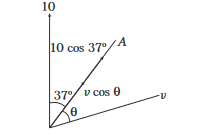
Time taken by the plane to move from \(O\) to \(A\),
\(
t=\frac{d}{10 \cos 37^{\circ}+v \cos \theta}=\frac{d}{8+v \cos \theta}
\)

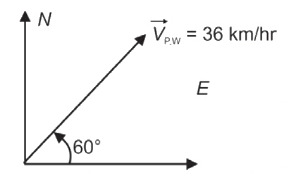
Example 30: The velocity of an aeroplane \(P\) relative to the steady wind is \(36 \mathrm{~km} / \mathrm{hr}\) in the direction 60 degree north of east . the velocity of another aeroplane \(Q\) relative to the same wind is \(18 \mathrm{~km} / \mathrm{hr}\) 60 degree south of west . the speed of aeroplane \(P\) wrt. aeroplane \(Q\) will be:

Answer: \(\overrightarrow{\mathrm{V}}_{PW}=\) velocity of \(\mathrm{P}\) w.r.t. wind
\(\overrightarrow{\mathrm{v}}_{{QW}}=\) velocity of \(\mathrm{Q}\) w.r.t. wind

\(
\begin{array}{l}
\vec{V}_{PW}=36 \cos 60 \hat{i}+36 \sin 60 \hat{j} \\
=36 \times \frac{1}{2} \hat{i}+36 \times \frac{\sqrt{3}}{2} \hat{j} \\
\vec{V}_{PW}=(18 \hat{i}+18 \sqrt{3} \hat{j}) k m / h r
\end{array}
\)

\(
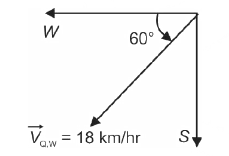
\begin{array}{l}
\quad \vec{V}_{QW}=-18 \cos 60 \hat{i}-18 \sin 60 \hat{j} \\
=-18 \times \frac{1}{2} \hat{i}-18 \times \frac{\sqrt{3}}{2} \hat{j} \\
\therefore \quad \vec{V}_{QW}=-9 \hat{i}-9 \sqrt{3} \hat{j}
\end{array}
\)
\(
\begin{array}{l}
\vec{V}_{PQ}=\vec{V}_{PW}-\vec{V}_{QW}=(18 \hat{i}+18 \sqrt{3} \hat{j})-(-9 \hat{i}-9 \sqrt{3} \hat{j}) \\
=27 \hat{i}+18 \sqrt{3} \hat{j}+9 \sqrt{3} \hat{j}=27 \hat{i}+27 \sqrt{3} \hat{j}
\end{array}
\)
Velocity of \(P\) w.r.t. \(Q=\vec{V}_{PQ}=27 \hat{i}+27 \sqrt{3} \hat{j}\)
\(\begin{aligned} \therefore \quad\left|\vec{V}_{P, Q}\right| & =\sqrt{27^2+(27 \sqrt{3})^2}=27 \sqrt{1+3} \\ & =27 \times 2=54 \mathrm{~km} / \mathrm{hr} \\ & =54 \times \frac{5}{18} \mathrm{~m} / \mathrm{s}=15 \mathrm{~m} / \mathrm{s}\end{aligned}\)