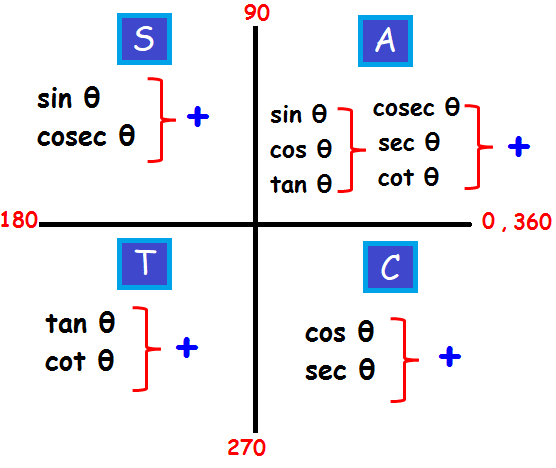
Quadrant Rules

Let us learn an easy way to remember where the trigonometric functions are positive and where they are negative.

The sine function: since \(\sin \theta=y\), sine is positive when \(y>0\). This occurs in Quadrants I and II.
The cosine function: since \(\cos \theta=x\), cosine is positive when \(x>0\). This occurs in Quadrants I and IV.
The tangent function: since \(\tan \theta=\frac{y}{x}\), tangent is positive when \(x\) and \(y\) are both positive or both negative. This occurs in Quadrants I and III.

We can summarize this information by quadrant:

In short, we call this ASTC Rule: ASTC rule is nothing but “all sin tan cos” rule in trigonometry. 

Quadrant I: sine, cosine, and tangent are positive.

Quadrant II: sine is positive (cosine and tangent are negative).

Quadrant III: tangent is positive (sine and cosine are negative).

Quadrant IV: cosine is positive (sine and tangent are negative).

Example 1: \(\text { What signs are } \tan 200^{\circ} \text { and } \cos 200^{\circ}?\)

Solution:

Since \(200^{\circ}=180^{\circ}+20^{\circ}, 200^{\circ}\) is in Quadrant III.
Tangent is positive, so \(\tan 200^{\circ}\) is positive.
Sine and cosine are negative in Quadrant III, so \(\cos 200^{\circ}\) is negative.

Therefore, \(\tan 200^{\circ}\) is positive and \(\cos 200^{\circ}\) is negative.

Example 2: In which quadrant must an angle lie if its sine is positive and its tangent is negative?

Solution: sine is positive in Quadrants I and II. Tangent is positive in Quadrant I, but negative in Quadrant II.

Example 3: What signs are \(\cos \left(-25^{\circ}\right)\) and \(\sec \left(-25^{\circ}\right)?\)

Solution: They are both positive. Angle \(-25^{\circ}\) is in Quadrant IV. In Quadrant IV cosine is positive. Since secant is the reciprocal of cosine, it is also positive.