Pythagorean Theorem

The Pythagorean Theorem says that, in a right triangle, the square of a (\(\mathbf{a}^2\) ) plus the square of \(\mathbf{b}\left(\mathbf{b}^2\right)\) is equal to the square of \(\mathbf{c}\left(\mathbf{c}^2\right)\):

\(a^2+b^2=c^2\)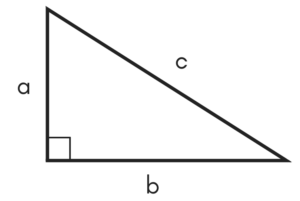

Here \(c\) is denoting the length of the hypotenuse and \(a\) and \(b\) are denoting the lengths of the perpendicular and the base. Therefore,
\(
\text { Hypotenuse }^2=\text { Perpendicular }{ }^2+\text { Base }^2
\)

Proof of Pythagorean Theorem

We can show that \(\mathbf{a}^2+\mathbf{b}^2=\mathbf{c}^2\) using Algebra
Let’s look at the diagram below, it has that “abc” triangle in it (four of them actually):

 

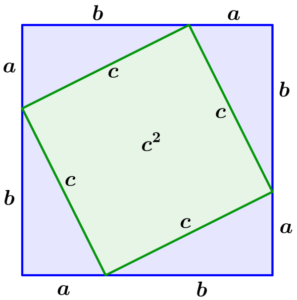
Area of Whole Square [outer square with sides (a+b) and (a+b)]:

It is a big square, with each side having a length of \(\mathbf{a}+\mathbf{b}\), so the total area is:
\(A=(a+b)(a+b)\)

Total area (Area of 4 Smaller triangles + green square with side c):

Each of the four triangles has an area of \((a b / 2)\)
So, all four of them together is: \(4 \times (a b / 2)=2 a b\)

The green square has an area of \(c^2\)

Therefore the total area \(A=c^2+2 a b\)

Both Areas Must Be Equal

The area of the large square(outer square) is equal to the area of the tilted square and the 4 triangles. This can be written as:
\(
(a+b)(a+b)=c^2+2 a b
\)
Now, let us rearrange this to see if we can get the Pythagoras theorem:
Start with: \((a+b)(a+b)=c^2+2 a b\)
Expand \((a+b)(a+b): a^2+2 a b+b^2=c^2+2 a b\)
Subtract “2ab” from both sides: \(a^2+b^2=c^2\)

Example 1: A right triangle has legs of lengths 4 cm and 3 cm. What is the length of its hypotenuse?

Solution:

\(
\begin{gathered}
c^2=a^2+b^2 \\
c^2=4^2+3^2 \\
c^2=16+9 \\
c^2=25 \\
c=5
\end{gathered}
\)

The hypotenuse measures 5 cm.

Example 2: Ashok wants to clean the window of his building, which is located 4 m high from the ground. He has a ladder that is 4.5 m. How far from the building should he place the ladder?

Solution:

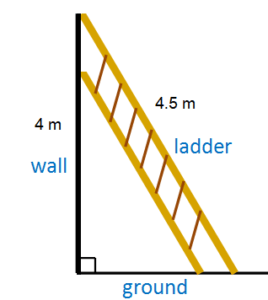
The length of the ladder is fixed and when placing it inclined in the building, we form a right triangle, where the ladder is the hypotenuse, the building is the height and the base is the distance from the building to the ladder. Therefore, we have the following values:
\(a=4\)
\(c=4.5\)
We have to use the Pythagorean theorem to find the value of \(b\) :
\(
\begin{gathered}
c^2=a^2+b^2 \\
4.5^2=4^2+b^2 \\
20.25=16+b^2 \\
b^2=20.25-16 \\
b^2=4.25 \\
b=2.06
\end{gathered}
\)
The distance from the building to where the ladder should be placed is \(2.06 \mathrm{~m}\).

Example 3: A person has to walk \(100 \mathrm{~m}\) to go from the position \(X\) in the north of east direction to the position \(Y\) and then to the west of \(Y\) to reach finally at position \(Z\). The position \(Z\) is situated at the north of \(X\) and at a distance of \(60 \mathrm{~m}\) from \(X\). Find the distance between \(X\) and \(Y\).

Solution:

Let us draw the diagram of the person’s movement from x to z

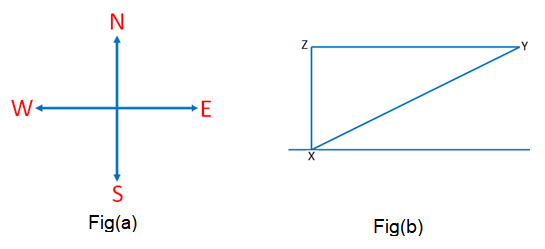
Let \(X Y=x {~m}\)
Therefore, \(Y Z=(100-x) m\)
In \(\triangle \mathrm{XYZ}, \angle \mathrm{Z}=90^{\circ}\)
Therefore, by Pythagoras’ theorem
\(
\begin{aligned}
&(X Y)^2=(Y Z)^2+(X Z)^2 \\
&\Rightarrow x^2=(100-x)^2+60^2 \\
&\Rightarrow x^2=10000-200 x+x^2+3600 \\
&\Rightarrow 200 x=10000+3600 \\
&\Rightarrow 200 x=13600 \\
&\Rightarrow x=13600 / 200 \\
&\Rightarrow x=68
\end{aligned}
\)
Therefore, distance between \(X\) and \(Y=68\) meters.

Example 4:  The height of two buildings is 34 m and 29 m respectively. If the distance between the two buildings is 12 m, find the distance between their tops.

Solution:

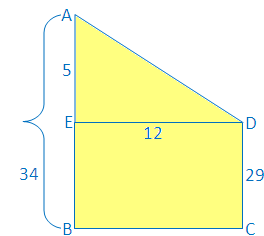
The vertical buildings \(A B\) and \(C D\) are \(34 \mathrm{~m}\) and \(29 \mathrm{~m}\) respectively.
Draw \(\mathrm{DE}\) \(\perp \mathrm{AB}\)
Then \(\mathrm{AE}=\mathrm{AB}-\mathrm{EB}\) but \(\mathrm{EB}=\mathrm{DC}\)
Therefore \(\mathrm{AE}=34 \mathrm{~m}-29 \mathrm{~m}=5 \mathrm{~m}\)
Now, AED is a right-angled triangle and right-angled at \(E\).
Therefore,
\(
A D^2=A E^2+E D^2
\)
\(
\begin{aligned}
&\Rightarrow A D^2=5^2+12^2 \\
&\Rightarrow A D^2=25+144
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow A D^2=169 \\
&\Rightarrow A D=\sqrt{ } 169 \\
&\Rightarrow A D=13
\end{aligned}
\)
Therefore the distance between their tops \(=13 \mathrm{~m}\).

Example 5: Does a triangle having 3 sides 8 m, 15 m, and 16 m have a Right Angle?

Solution:

Does \(8^2+15^2=16^2?\)
\(8^2+15^2=64+225=289\), Does it have a right angle?
but \(16^2=256\)
Since it does not satisfy the Pythagorean theorem, it does not have a right angle.