Pythagorean Identities

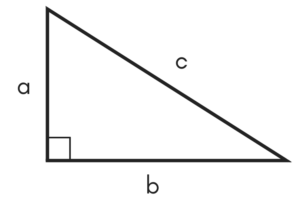
We can now derive the three important Pythagorean identities of trigonometric ratios. The Pythagoras theorem states that in a right-angled triangle the square of the hypotenuse is equal to the sum of the square of the other two sides. 

\(
\begin{aligned}
&\frac{a^2}{c^2}+\frac{b^2}{c^2}=\frac{c^2}{c^2} \\
&\left(\frac{a}{c}\right)^2+\left(\frac{b}{c}\right)^2=1 \\
&(\sin \theta)^2+(\cos \theta)^2=1 \\
&\sin ^2 \theta+\cos ^2 \theta=1 \dots(1)
\end{aligned}
\)
\(
\begin{aligned}
&\frac{\sin ^2 \theta}{\cos ^2 \theta}+\frac{\cos ^2 \theta}{\cos ^2 \theta}=\frac{1}{\cos ^2 \theta} \\
&\tan ^2 \theta+1=\sec ^2 \theta \dots(2)
\end{aligned}
\)
\(
\begin{aligned}
&\frac{\sin ^2 \theta}{\sin ^2 \theta}+\frac{\cos ^2 \theta}{\sin ^2 \theta}=\frac{1}{\sin ^2 \theta} \\
&1+\cot ^2 \theta=\csc ^2 \theta \dots(3)
\end{aligned}
\)

Thus the three important Pythagorean Identities are
\(
\begin{aligned}
&\sin ^2 \theta+\cos ^2 \theta=1 \\
&\tan ^2 \theta+1=\sec ^2 \theta \\
&1+\cot ^2 \theta=\csc ^2 \theta
\end{aligned}
\)