Motion in a plane (Two-dimensional Motion)

Two Dimensional Motion is the motion of the particle in a fixed plane. Unlike rectilinear motion where particle moves in a straight line, here particles moves along in the x-y plane. Both x and y coordinates of the particles changes with time. Examples of Motion in Two dimensions are Projectile motion (Motion of the football ) ,Circular Motion ( earth motion around the sun), Motion of a billiard ball on the billiard table, Motion of the boat etc.

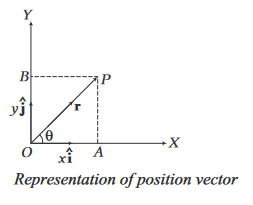
A vector that extends from a reference point to the point at which particle is located is called position vector.
Let \(\mathbf{r}\) be the position vector of a particle \(P\) located in a plane with reference to the origin \(O\) in \(X Y\)-plane as shown in the figure.

\(
\mathbf{OP}=\mathbf{OA}+\mathbf{OB}
\)
Position vector, \(\mathbf{r}=x \hat{\mathbf{i}}+y \hat{\mathbf{j}}\)
Direction of this position vector \(\mathbf{r}\) is given by the angle \(\theta\) with \(X\)-axis, where
\(
\tan \theta=\left(\frac{y}{x}\right)
\)
\(
\theta=\tan ^{-1}\left(\frac{y}{x}\right)
\)
In three dimensions, the position vector is represented as
\(
\mathbf{r}=x \hat{\mathbf{i}}+y \hat{\mathbf{j}}+z \hat{\mathbf{k}}
\)

Example 1: A particle moves in a plane such that its coordinates changes with time as \(x=a t\) and \(y=b t\), where a and \(b\) are constants. Find the position vector of the particle and its direction at any time t.

Answer: Coordinates of the particle are \(x=a t\) and \(y=b t\)
\(\therefore \quad\) Position vector of the particle at any time \(t\) is
\(
\mathbf{r}=x \hat{\mathbf{i}}+y \hat{\mathbf{j}}=(a t) \hat{\mathbf{i}}+(b t) \hat{\mathbf{j}}
\)
Direction of \(\mathbf{r}, \theta=\tan ^{-1}\left(\frac{y}{x}\right)=\tan ^{-1}\left(\frac{b t}{a t}\right)=\tan ^{-1}\left(\frac{b}{a}\right)\)

Displacement vector

Consider a particle moving in \(X Y\)-plane with a uniform velocity \(\mathbf{v}\) and point \(O\) as an origin for measuring time and position of the particle. Let the particle be at positions \(A\) and \(B\) at timings \(t_1\) and \(t_2\), respectively. The position vectors are \(\mathbf{O A}=\mathbf{r}_1\) and \(\mathbf{O B}=\mathbf{r}_2\).

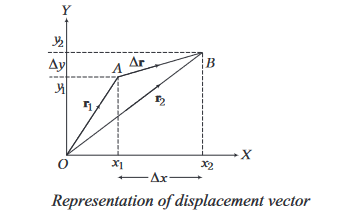
Then, the displacement of the particle in time interval \(\left(t_2-t_1\right)\) is \(\mathbf{A B}\). From triangle law of vector addition, we get
\(
\begin{aligned}
\mathbf{O A}+\mathbf{A B} & =\mathbf{O B} \\
\mathbf{A B} & =\mathbf{O B}-\mathbf{O A} \\
\mathbf{A B} & =\mathbf{r}_2-\mathbf{r}_1 \dots(i)
\end{aligned}
\)
If the coordinates of the particle at points \(A\) and \(B\) are \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\), then
\(
\begin{array}{l}
\mathbf{r}_1=x_1 \hat{\mathbf{i}}+y_1 \hat{\mathbf{j}} \\
\mathbf{r}_2=x_2 \hat{\mathbf{i}}+y_2 \hat{\mathbf{j}}
\end{array}
\)
and Substituting the values of \(\mathbf{r}_1\) and \(\mathbf{r}_2\) in Eq. (i), we get
\(
\mathbf{A B}=\left(x_2 \hat{\mathbf{i}}+y_2 \hat{\mathbf{j}}\right)-\left(x_1 \hat{\mathbf{i}}+y_1 \hat{\mathbf{j}}\right)
\)
Displacement, \(\mathbf{A B}=\left(x_2-x_1\right) \hat{\mathbf{i}}+\left(y_2-y_1\right) \hat{\mathbf{j}}\)
or Displacement, \(\Delta \mathbf{r}=\Delta x \hat{i}+\Delta y \hat{\mathbf{j}}\)
Magnitude of displacement, \(|\Delta \mathbf{r}|=\sqrt{(\Delta x)^2+(\Delta y)^2}\)
\(
=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}
\)

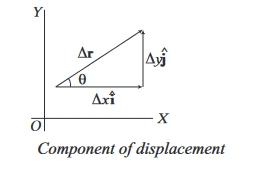
Direction of the displacement vector \(\Delta \mathbf{r}\) is given by
\(
\tan \theta=\frac{\Delta y}{\Delta x} \Rightarrow \theta=\tan ^{-1}\left(\frac{\Delta y}{\Delta x}\right)
\)
where, \(\theta=\) angle made by \(\Delta \mathbf{r}\) with \(X\)-axis.
Similarly, in three dimensions, the displacement vector can be represented as
\(
\Delta \mathbf{r}=\left(x_2-x_1\right) \hat{\mathbf{i}}+\left(y_2-y_1\right) \hat{\mathbf{j}}+\left(z_2-z_1\right) \hat{\mathbf{k}}
\)
Note: Magnitude of displacement \((\Delta r)\) between two points is always less than or equal to distance (s) between corresponding points. i.e.
\(
\Delta r \leq s
\)

Example 2: An object moves from position \((3,4)\) to \((6,5)\) in the \(X Y\)-plane. Find the magnitude and direction of displacement vector of the particle.

Answer: Position vectors of the particle are
\(
\mathbf{r}_1=x_1 \hat{\mathbf{i}}+y_1 \hat{\mathbf{j}}=3 \hat{\mathbf{i}}+4 \hat{\mathbf{j}} \text { and } \mathbf{r}_2=x_2 \hat{\mathbf{i}}+y_2 \hat{\mathbf{j}}=6 \hat{\mathbf{i}}+5 \hat{\mathbf{j}}
\)
\(\therefore\) Displacement vector, \(\Delta \mathbf{r}=\left(x_2-x_1\right) \hat{\mathbf{i}}+\left(y_2-y_1\right) \hat{\mathbf{j}}\)
\(
=(6-3) \hat{\mathbf{i}}+(5-4) \hat{\mathbf{j}}=3 \hat{\mathbf{i}}+\hat{\mathbf{j}}
\)
\(\therefore\) Magnitude of displacement vector,
\(
|\Delta \mathbf{r}|=\sqrt{(3)^2+(1)^2}=\sqrt{10}
\)
Direction of \(\Delta \mathbf{r}\) with \(X\)-axis,
\(
\theta=\tan ^{-1}\left(\frac{\Delta y}{\Delta x}\right)=\tan ^{-1}\left(\frac{1}{3}\right) \approx 18.43^{\circ}
\)

Velocity vector

Velocity of an object in motion is defined as the ratio of displacement and the corresponding time interval taken by the object, i.e.
\(
\text { Velocity }=\frac{\text { Displacement }}{\text { Time interval }}
\)
Velocity is a vector quantity as it has both the magnitude (speed) and direction.
It is of two types
(i) Average velocity
(ii) Instantaneous velocity

Average velocity

It is defined as the ratio of the displacement and the corresponding time interval.
Thus, average velocity \(=\frac{\text { displacement }}{\text { time taken }}\)
Average velocity, \(\mathbf{v}_{\text {av }}=\frac{\Delta \mathbf{r}}{\Delta t}=\frac{\mathbf{r}_2-\mathbf{r}_1}{t_2-t_1}\)

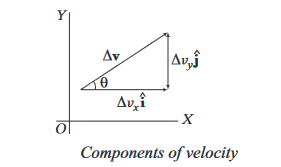
Velocity can be expressed in the component form as
\(
\mathbf{v}_{\mathrm{av}}=\frac{\Delta x}{\Delta t} \hat{\mathbf{i}}+\frac{\Delta y}{\Delta t} \hat{\mathbf{j}}=\Delta v_x \hat{\mathbf{i}}+\Delta v_y \hat{\mathbf{j}}
\)
where, \(\Delta v_x\) and \(\Delta v_y\) are the components of average velocity along \(x\)-direction and \(y\)-direction, respectively. The magnitude of \(\mathbf{v}_{\mathrm{av}}\) is given by
\(
v_{\mathrm{av}}=\sqrt{\Delta v_x^2+\Delta v_y^2}
\)
and the direction of \(\mathbf{v}_{\text {av }}\) is given by angle \(\theta\)
\(
\tan \theta=\frac{\Delta v_y}{\Delta v_x} \text { (From } X \text {-axis) }
\)

Example 3: A particle moves in XY-plane from position \((1 \mathrm{~m}, 2 \mathrm{~m})\) to \((3 \mathrm{~m}, 4 \mathrm{~m})\) in \(2 \mathrm{~s}\). Find the magnitude and direction of average velocity.

Answer: Given, position vectors of the particle are
\(
\begin{aligned}
\mathbf{r}_1 & =x_1 \hat{\mathbf{i}}+y_1 \hat{\mathbf{j}}=\hat{\mathbf{i}}+2 \hat{\mathbf{j}} \\
\mathbf{r}_2 & =x_2 \hat{\mathbf{i}}+y_2 \hat{\mathbf{j}}=3 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}
\end{aligned}
\)
Displacement, \(\Delta \mathbf{r}=\mathbf{r}_2-\mathbf{r}_1=2 \hat{\mathbf{i}}+2 \hat{\mathbf{j}}\)
\(\therefore\) Average velocity, \(\mathbf{v}_{\mathrm{av}}=\frac{\Delta \mathbf{r}}{\Delta t}\)
\(
\Rightarrow \quad \mathbf{v}_{\text {av }}=\frac{2 \hat{\mathbf{i}}+2 \hat{\mathbf{j}}}{2}
\)
\(
\Rightarrow \quad \mathbf{v}_{\mathrm{av}}=\Delta v_x \hat{\mathbf{i}}+\Delta v_y \hat{\mathbf{j}}=(\hat{\mathbf{i}}+\hat{\mathbf{j}}) \mathrm{ms}^{-1}
\)
\(\Rightarrow \quad\left|\mathbf{v}_{\mathrm{av}}\right|=\sqrt{(1)^2+(1)^2}=\sqrt{2} \mathrm{~ms}^{-1}\)
Direction of average velocity with \(X\)-axis,
\(
\theta=\tan ^{-1}\left(\frac{\Delta v_y}{\Delta v_x}\right)=\tan ^{-1}\left(\frac{1}{1}\right)=45^{\circ}
\)

Instantaneous velocity

The velocity of the object at an instant of time \((t)\) is known as instantaneous velocity. The average velocity will become instantaneous, if \(\Delta t\) approaches to zero.
\(\therefore\) Instantaneous velocity,
\(
\mathbf{v}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \mathbf{r}}{\Delta t}=\frac{d \mathbf{r}}{d t}
\)
Now, we can write
\(
\begin{array}{l}
d \mathbf{r}=d x \hat{\mathbf{i}}+d y \hat{\mathbf{j}} \\
\therefore \quad \mathbf{v}=\frac{d x \hat{\mathbf{i}}+d y \hat{\mathbf{j}}}{d t}=\frac{d x}{d t} \hat{\mathbf{i}}+\frac{d y}{d t} \hat{\mathbf{j}} \\
\end{array}
\)
\(
\Rightarrow \quad \mathbf{v}=v_x \hat{\mathbf{i}}+v_y \hat{\mathbf{j}}
\)
Similarly, in three dimensions, we can write
\(
\mathbf{v}=v_x \hat{\mathbf{i}}+v_y \hat{\mathbf{j}}+v_z \hat{\mathbf{k}}
\)
where, \(v_x=\frac{d x}{d t}\) is magnitude of instantaneous velocity in \(v_y=\frac{d y}{d t}\) is magnitude of instantaneous velocity in and \(\quad v_z=\frac{d z}{d t}\) is magnitude of instantaneous velocity in \(z\)-direction.
Magnitude of instantaneous velocity, \(|\mathbf{v}|=\sqrt{v_x^2+v_y^2}\)
Direction of instantaneous velocity \(\mathbf{v}\) with \(X\)-axis,

\(
\tan \theta=\frac{v_y}{v_x} \Rightarrow \theta=\tan ^{-1}\left(\frac{v_y}{v_x}\right)
\)

Example 4: Position vector of a particle is given as
\(
\mathbf{r}=2 t \hat{\mathbf{i}}+3 t^2 \hat{\mathbf{j}}
\)
where, \(t\) is in seconds and the coefficients have the proper units, for \(r\) to be in metres.
(i) Find instantaneous velocity \(\mathbf{v}(t)\) of the particle.
(ii) Find magnitude and direction of \(\mathbf{v}(t)\) at \(t=2 \mathrm{~s}\).

Answer: Given, \(\mathbf{r}=2 t \hat{\mathbf{i}}+3 t^2 \hat{\mathbf{j}}\)
(i) Instantaneous velocity, \(\mathbf{v}(t)=\frac{d \mathbf{r}}{d t}=\frac{d}{d t}\left(2 \hat{\mathbf{i}}+3 t^2 \hat{\mathbf{j}}\right)\)
\(
\Rightarrow \quad \mathbf{v}=v_x \hat{\mathbf{i}}+v_y \hat{\mathbf{j}}=2 \hat{\mathbf{i}}+6 t \hat{\mathbf{j}}
\)
(ii) Magnitude of \(\mathbf{v}(t)\),
\(
|\mathbf{v}(t)|=\sqrt{v_x^2+v_y^2}=\sqrt{(2)^2+(6 t)^2}=\sqrt{4+36 t^2}
\)
At \(t=2 \mathrm{~s}, \quad|\mathrm{v}(t)|=\sqrt{4+36 \times 4}=\sqrt{148} \mathrm{~ms}^{-1}\)
Direction of \(\mathbf{v}(t), \theta=\tan ^{-1}\left(\frac{v_y}{v_x}\right)=\tan ^{-1}\left(\frac{6 t}{2}\right)=\tan ^{-1}(3 t)\)
At \(t=2 \mathrm{~s}, \quad \theta=\tan ^{-1}(3 \times 2) \approx \tan ^{-1}(6) \mathrm{rad}\)

Acceleration vector

It is defined as the rate of change of velocity. It can be expressed as
\(
\text { Acceleration }=\frac{\text { Change in velocity }}{\text { Time taken }}
\)
It is of two types as follows
(i) Average acceleration
(ii) Instantaneous acceleration

Average acceleration

It is defined as the change in velocity \((\Delta \mathbf{v})\) divided by the corresponding time interval \((\Delta t)\). It can be expressed as

Average acceleration, \(\mathbf{a}_{\mathrm{av}}=\frac{\Delta \mathbf{v}}{\Delta t}=\frac{\Delta v_x \hat{\mathbf{i}}+\Delta v_y \hat{\mathbf{j}}}{\Delta t}\)
\(
=\frac{\Delta v_x}{\Delta t} \hat{\mathbf{i}}+\frac{\Delta v_y}{\Delta t} \hat{\mathbf{j}}
\)
\(
\text { Average acceleration }=\mathbf{a}_{(a v) x} \hat{\mathbf{i}}+\mathbf{a}_{(\text {av) } y} \hat{\mathbf{j}}
\)
which is expressed in component form
where, \(\mathbf{a}_{(\mathrm{av}) x}=\frac{\Delta v_x}{\Delta t}=\) average acceleration in \(x\)-direction and \(\mathbf{a}_{(\mathrm{av}) y}=\frac{\Delta v_y}{\Delta t}=\) average acceleration in \(y\)-direction.
In three dimensions, we can write
\(
\mathbf{a}_{\mathrm{av}}=a_{(\mathrm{av}) x} \hat{\mathbf{i}}+a_{(\mathrm{av}) y} \hat{\mathbf{j}}+a_{(\mathrm{av}) z} \hat{\mathbf{k}}
\)
Angle \(\theta\) made by average acceleration with \(X\)-axis is
\(
\tan \theta=\frac{a_{(\mathrm{av}) y}}{a_{(\mathrm{av}) x}} \Rightarrow \theta=\tan ^{-1}\left(\frac{a_{(\mathrm{av}) y}}{a_{(\mathrm{av}) x}}\right)
\)

Example 5: Velocity of a particle changes from \((3 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}) \mathrm{m} / \mathrm{s}\) to \((6 \hat{\mathbf{i}}+5 \hat{\mathbf{j}}) \mathrm{m} / \mathrm{s}\) in \(2 \mathrm{~s}\). Find magnitude and direction of average acceleration.

Answer: Given, velocity vectors of the particle,
\(
\begin{array}{l}
\qquad \mathbf{v}_1=3 \hat{\mathbf{i}}+4 \hat{\mathbf{j}} \\
\text { and } \mathbf{v}_2=6 \hat{\mathbf{i}}+5 \hat{\mathbf{j}} \\
\text { Change in velocity, } \\
\Delta \mathbf{v}_x=\left(v_2\right)_x-\left(v_1\right)_x \hat{\mathbf{i}}=(6-3) \hat{\mathbf{i}}=3 \hat{\mathbf{i}} \\
\Delta \mathbf{v}_y\left.=\left(v_2\right)_y-\left(v_1\right)_y\right) \hat{\mathbf{j}}=(5-4) \hat{\mathbf{j}}=\hat{\mathbf{j}} \\
\therefore \Delta \mathbf{v}=\Delta \mathbf{v}_x+\Delta \mathbf{v}_y=3 \hat{\mathbf{i}}+\hat{\mathbf{j}}
\end{array}
\)
Change in velocity,
\(
\begin{aligned}
\Delta \mathbf{v}_x & =\left(v_2\right)_x-\left(v_1\right)_x \hat{\mathbf{i}}=(6-3) \hat{\mathbf{i}}=3 \hat{\mathbf{i}} \\
\Delta \mathbf{v}_y & \left.=\left(v_2\right)_y-\left(v_1\right)_y\right) \hat{\mathbf{j}}=(5-4) \hat{\mathbf{j}}=\hat{\mathbf{j}} \\
\therefore \Delta \mathbf{v} & =\Delta \mathbf{v}_x+\Delta \mathbf{v}_y=3 \hat{\mathbf{i}}+\hat{\mathbf{j}}
\end{aligned}
\)
Average acceleration,
\(
\begin{aligned}
\mathbf{a}_{\mathrm{av}} & =\frac{\Delta \mathbf{v}}{\Delta t}=\frac{3 \hat{\mathbf{i}}+\hat{\mathbf{j}}}{2} \\
& =1.5 \hat{\mathbf{i}}+0.5 \hat{\mathbf{j}}
\end{aligned} \quad(\because t=2 \mathrm{~s})
\)
Direction of average acceleration,
\(
\begin{aligned}
\tan \theta & =\frac{a_{(\mathrm{av}) y}}{a_{(\mathrm{av}) x}}=\frac{0.5}{1.5}=\frac{1}{3} \\
\Rightarrow \quad \theta & =\tan ^{-1}\left(\frac{1}{3}\right) \\
& \approx 18.43^{\circ} \text { with } X \text {-axis }
\end{aligned}
\)

Instantaneous acceleration

It is defined as the limiting value of the average acceleration as the time interval approaches to zero.
It can be expressed as
\(
\mathbf{a}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \mathbf{v}}{\Delta t}=\frac{d \mathbf{v}}{d t}
\)
Instantaneous acceleration,
where,
\(
\mathbf{a}=a_x \hat{\mathbf{i}}+a_y \hat{\mathbf{j}}
\)
\(a_x=\) magnitude of instantaneous acceleration in \(x\)-direction
\(
=\frac{d v_x}{d t}
\)
\(a_y=\) magnitude of instantaneous acceleration in \(y\)-direction
\(
=\frac{d v_y}{d t}
\)
The magnitude of instantaneous acceleration is given by
\(
a=\sqrt{a_x^2+a_y^2}
\)
If acceleration a makes an angle \(\theta\) with \(X\)-axis, then
\(
\tan \theta=\frac{a_y}{a_x} \Rightarrow \theta=\tan ^{-1}\left(\frac{a_y}{a_x}\right)
\)

In three dimensions, we can write
\(
\mathbf{a}=a_x \hat{\mathbf{i}}+a_y \hat{\mathbf{j}}+a_z \hat{\mathbf{k}}
\)

Example 6: The position of a particle is given by
\(
\mathbf{r}=3 t \hat{\mathbf{i}}+2 t^2 \hat{\mathbf{j}}+8 \hat{\mathbf{k}}
\)
where, \(t\) is in seconds and the coefficients have the proper units for \(r\) to be in metres.
(i) Find \(v(t)\) and \(a(t)\) of the particle.
(ii) Find the magnitude and direction of \(v(t)\) and \(a(t)\) at \(t=1 \mathrm{~s}\).

Answer: Position of particle, \(\mathbf{r}=3 t \hat{\mathbf{i}}+2 t^2 \hat{\mathbf{j}}+8 \hat{\mathbf{k}}\)
(i)
\(
\begin{aligned}
\text { As, } \mathbf{v}(t) & =\frac{d \mathbf{r}}{d t} \text { and } \mathbf{a}(t)=\frac{d \mathbf{v}}{d t} \\
\therefore \quad \mathbf{v}(t) & =\frac{d}{d t}\left(3 t \hat{\mathbf{i}}+2 t^2 \hat{\mathbf{j}}+8 \hat{\mathbf{k}}\right)=3 \hat{\mathbf{i}}+4 t \hat{\mathbf{j}} \\
\mathbf{a}(t) & =\frac{d v}{d t}=4 \hat{\mathbf{j}}
\end{aligned}
\)
(ii) \(v(t)=\sqrt{v_x^2+v_y^2}\) and \(\theta=\tan ^{-1}\left(\frac{v_y}{v_x}\right)\)
Velocity, \(\mathbf{v}(t)=3 \hat{\mathbf{i}}+4 t \hat{\mathbf{j}}\)
At \(t=1 \mathrm{~s}\),
\(
v=\sqrt{(3)^2+(4)^2}=5 \mathrm{~ms}^{-1}
\)
\(\Rightarrow\) Direction of \(v(t)=\theta=\tan ^{-1}\left(\frac{4}{3}\right)=53^{\circ}\) with \(X\)-axis
Direction of \(a(t)\), at \(t=1 \mathrm{~s}\),
\(\theta^{\prime}=\tan ^{-1}\left(\frac{a_y}{a_x}\right)=\tan ^{-1}\left(\frac{4}{0}\right)=\tan ^{-1}(\infty)=90^{\circ}\) with \(X\)-axis.

Motion in plane with uniform acceleration

An object is said to be moving with uniform acceleration, if its velocity vector undergoes the same change in the same interval of time (however small).
Let an object is moving in \(X Y\)-plane and its acceleration a is constant. At time \(t=0\), the velocity of an object be \(\mathbf{v}_0\) (say) and \(\mathbf{v}\) be the velocity at time \(t\).
According to definition of average acceleration, we get
\(
\mathbf{a}=\frac{\mathbf{v}-\mathbf{v}_0}{t-0}=\frac{\mathbf{v}-\mathbf{v}_0}{t} \Rightarrow \mathbf{v}=\mathbf{v}_0+\mathbf{a} t
\)
In terms of rectangular components, we can express it as
\(
v_x=v_{0 x}+a_x t \text { and } v_y=v_{0 y}+a_y t
\)
It can be concluded that, each rectangular component of velocity of an object moving with uniform acceleration in a plane depends upon time as if it were the velocity vector of one dimensional uniformly accelerated motion.

Path of particle under constant acceleration

Now, we can also find the position vector \((\mathbf{r})\). Let \(\mathbf{r}_0\) and \(\mathbf{r}\) be the position vectors of the particle at time \(t=0\) and \(t=t\) and their velocities at these instants be \(\mathbf{v}_0\) and \(\mathbf{v}\), respectively. Then, the average velocity is given by
\(
\mathbf{v}_{\mathrm{av}}=\frac{\mathbf{v}_0+\mathbf{v}}{2}
\)
Displacement is the product of average velocity and time interval. It is expressed as
\(
\mathbf{r}-\mathbf{r}_0=\left(\frac{\mathbf{v}+\mathbf{v}_0}{2}\right) t=\left[\frac{\left(\mathbf{v}_0+\mathbf{a} t\right)+\mathbf{v}_0}{2}\right] t
\)
\(
\mathbf{r}-\mathbf{r}_0=\mathbf{v}_0 t+\frac{1}{2} \mathbf{a} t^2
\)
\(
\mathbf{r}=\mathbf{r}_0+\mathbf{v}_0 t+\frac{1}{2} \mathbf{a} t^2
\)
In terms of rectangular components, we get
\(
x \hat{\mathbf{i}}+y \hat{\mathbf{j}}=x_0 \hat{\mathbf{i}}+y_0 \hat{\mathbf{j}}+\left(v_{0 x} \hat{\mathbf{i}}+v_{0 y} \hat{\mathbf{j}}\right) t+\frac{1}{2}\left(a_x \hat{\mathbf{i}}+a_y \hat{\mathbf{j}}\right) t^2
\)
Now, equating the coefficients of \(\hat{\mathbf{i}}\) and \(\hat{\mathbf{j}}\),
\(
x=x_0+v_{0 x} t+\frac{1}{2} a_x t^2 \ldots . . . \text { along } X \text {-axis }
\)
\(
\text { and } \quad y=y_0+v_{0 y} t+\frac{1}{2} a_y t^2 \ldots . . . \text { along } Y \text {-axis }
\)
Note: Motion in a plane (two dimensional motion) can be treated as two separate simultaneous one dimensional motions with constant acceleration along two perpendicular directions.

Example 7: (i) What does \(\left|\frac{d \mathbf{v}}{d t}\right|\) and \(\frac{d|\mathbf{v}|}{d t}\) represent?
(ii) Can these be equal?
(iii) Can \(\frac{d|\mathbf{v}|}{d t}=0\) while \(\left|\frac{d \mathbf{v}}{d t}\right| \neq 0\) ?
(iv) \(\operatorname{Can} \frac{d|\mathbf{v}|}{d t} \neq 0\) while \(\left|\frac{d \mathbf{v}}{d t}\right|=0\) ?

Answer: (i) \(\left|\frac{d \mathbf{v}}{d t}\right|\) is the magnitude of total acceleration. While \(\frac{d|\mathbf{v}|}{d t}\) represents the time rate of change of speed (called the tangential acceleration, a component of total acceleration) as \(|\mathbf{v}|=v\).
(ii) These two are equal in case of one dimensional motion (without change in direction).
(iii) In case of uniform circular motion, speed remains constant while velocity changes.
Hence, \(\frac{d|\mathbf{v}|}{d t}=0\) while \(\left|\frac{d \mathbf{v}}{d t}\right| \neq 0\).
(iv) \(\frac{d|\mathbf{v}|}{d t} \neq 0\) implies that speed of particle is not constant. Velocity cannot remain constant, if speed is changing. Hence, \(\left|\frac{d \mathbf{v}}{d t}\right|\) cannot be zero in this case. So, it is not possible to have \(\left|\frac{d \mathbf{v}}{d t}\right|=0\) while \(\frac{d|\mathbf{v}|}{d t} \neq 0\).

Example 8: \(A\) particle starts from origin at \(t=0\) with \(a\) velocity of \(15 \hat{\mathbf{i}} \mathrm{ms}^{-1}\) and moves in \(X Y\)-plane under the action of a force which produces a constant acceleration of \((15 \hat{\mathbf{i}}+20 \hat{\mathbf{j}}) \mathrm{ms}^{-2}\). Find the \(y\)-coordinate of the particle at the instant when its \(x\)-coordinate is \(180 \mathrm{~m}\).

Answer: The position of the particle is given by
\(
\mathbf{r}(t)=\mathbf{v}_0 t+\frac{1}{2} \mathbf{a} t^2=15 \hat{\mathbf{i}} t+\frac{1}{2}(15 \hat{\mathbf{i}}+20 \hat{\mathbf{j}}) t^2
\)
\(
\begin{aligned}
& =\left(15 t+7.5 t^2\right) \hat{\mathbf{i}}+10 t^2 \hat{\mathbf{j}} \\
\therefore \quad x(t) & =15 t+7.5 t^2 \text { and } y(t)=10 t^2
\end{aligned}
\)
If \(x(t)=180 \mathrm{~m}, t=\) ?
\(
180=15 t+7.5 t^2 \Rightarrow t=4 \mathrm{~s}
\)
\(\therefore y\)-coordinate, \(y(t)=10 \times 16=160 \mathrm{~m}\)

Example 9: An object has a velocity \(\mathbf{v}=(2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}) \mathrm{ms}^{-1}\) at time \(t=0 \mathrm{~s}\). It undergoes a constant acceleration \(a=(\hat{\mathbf{i}}-3 \hat{\mathbf{j}}) m s^{-2}\) for \(4 s\). Then,
(i) find the coordinates of the object, if it is at origin at \(t=0\).
(ii) find the magnitude of its velocity at the end of \(4 \mathrm{~s}\).

Answer: (i) Here, initial position of the object,
\(
\begin{array}{l}
\qquad \mathbf{r}_0=x_0 \hat{\mathbf{i}}+y_0 \hat{\mathbf{j}}=0 \hat{\mathbf{i}}+0 \hat{\mathbf{j}} \\
\text { Initial velocity, } \mathbf{v}_0=v_{0_x} \hat{\mathbf{i}}+v_{0_y} \hat{\mathbf{j}}=2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}} \\
\text { Acceleration, } \quad \mathbf{a}=a_x \hat{\mathbf{i}}+a_y \hat{\mathbf{j}}=\hat{\mathbf{i}}-3 \hat{\mathbf{j}} \\
\text { and } t=4 \mathrm{~s}
\end{array}
\)
Let the final coordinates of the object be \((x, y)\). Then, according to the equation for the path of particle under constant acceleration,
\(
\begin{aligned}
x & =x_0+v_{0 x} t+\frac{1}{2} a_x t^2=0+2 \times 4+\frac{1}{2}(1) \times 4^2 \\
\Rightarrow \quad x & =16 \mathrm{~m} \text { and } y=y_0+v_{0 y} t+\frac{1}{2} a_y t^2 \\
& =0+4 \times 4+\frac{1}{2}(-3) \times 4^2 \Rightarrow y=-8 \mathrm{~m}
\end{aligned}
\)
Therefore, the object lies at \((16 \hat{\mathbf{i}}-8 \hat{\mathbf{j}})\) at \(t=4 \mathrm{~s}\).
(ii) Using equation
\(
\begin{array}{l}
\mathbf{v}=\mathbf{v}_0+\mathbf{a} t \\
\Rightarrow \quad \mathbf{v}=(2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}})+(\hat{\mathbf{i}}-3 \hat{\mathbf{j}}) \times 4 \\
=(2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}})+(4 \hat{\mathbf{i}}-12 \hat{\mathbf{j}})=(2+4) \hat{\mathbf{i}}+(4-12) \hat{\mathbf{j}} \\
\Rightarrow \quad \mathbf{v}=6 \hat{\mathbf{i}}-8 \hat{\mathbf{j}} \\
\end{array}
\)
\(\therefore\) Magnitude of velocity, \(|\mathbf{v}|=\sqrt{6^2+8^2}=10 \mathrm{~ms}^{-1}\)
Its direction with \(X\)-axis, \(\theta=\tan ^{-1}\left(\frac{-8}{6}\right) \approx-53^{\circ}\)

Projectile 

When an object or body released into the space with some initial velocity, moves freely under the effect of gravity is known as projectile.

Motion of a particle under constant acceleration is either a straight line (one-dimensional) or parabolic (two-dimensional). Motion is one dimensional under following three conditions :

• Initial velocity of the particle is zero.
• Initial velocity of the particle is in the direction of constant acceleration (or parallel to it).
• Initial velocity of the particle is in the opposite direction of constant acceleration (or antiparallel to it).

For small heights acceleration due to gravity \((g)\) is almost constant. The three cases discussed about are as shown in the Figure below.

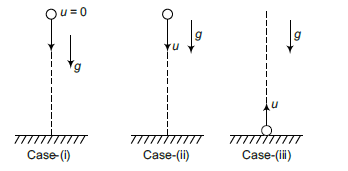
In all other cases when initial velocity is at some angle \(\left(\neq 0^{\circ}\right.\) or \(\left.180^{\circ}\right)\) with constant acceleration, motion is parabolic as shown below.

This motion under acceleration due to gravity is called projectile motion.

Projectile Motion

If a constant force (and hence, constant acceleration) acts on a particle at an angle \(\theta\left(\neq 0^{\circ}\right.\) or \(\left.180^{\circ}\right)\) with the direction of its initial velocity ( \(\neq\) zero), the path followed by the particle is parabolic and the motion of the particle is called projectile motion. It is a two dimensional motion, i.e. motion of the particle is constrained in a plane. In other words, if a particle moves in horizontal as well as vertical motion simultaneously, the motion of the particle is known as projectile motion.

Projectile motion is considered as two simultaneous motion in mutually perpendicular directions which are completely independent from each other i.e., horizontal motion and vertical motion

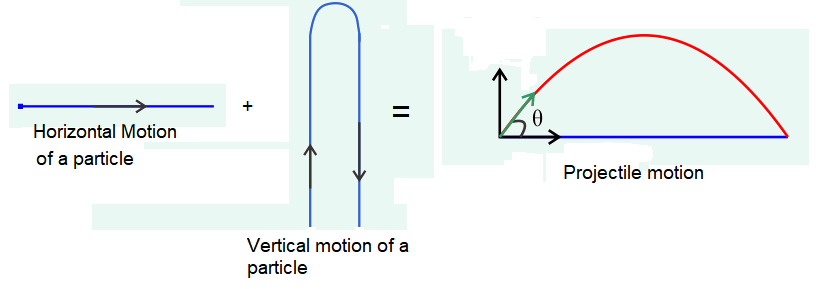
Note:

• If the angle between acceleration and velocity is \(\theta\) and where \(0^{\circ}<\theta<180^{\circ}\), then particle is executing projectile motion.
• In projectile motion, change in velocity of particle in magnitude and direction both act simultaneously.

When a particle is thrown obliquely near the earth’s surface, it moves in a parabolic path, provided that the particle remains close to the surface of earth and the air resistance is negligible. This is an example of projectile motion.

Parabolic Motion of Projectiles

Let us consider a ball projected at an angle \(\theta\) with respect to the horizontal \(x\)-axis with the initial velocity \(u\) as shown below:

Let \(O X\) be a horizontal line on the ground, \(O Y\) be a vertical line perpendicular to the ground and \(O\) be the origin for \(X Y\)-axes on a plane. Suppose an object is projected from point \(O\) with velocity \((u)\), making an angle \((\theta)\) with the horizontal direction \(O X\), such that \(x_0=0\) and \(y_0=0\) when \(t=0\).

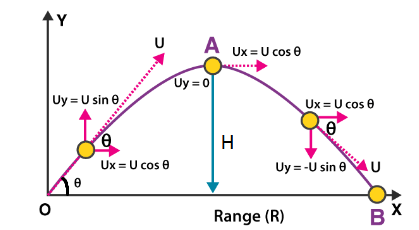
While resolving velocity \((u)\) into two components, we get

•  \(u \cos \theta\) along \(O X\) and
• \(u \sin \theta\) along \(O Y\)

As there is no force acting in horizontal direction, so the horizontal component of velocity \((u \cos \theta\) ) remains constant throughout the entire motion, so there is no acceleration in the horizontal direction (if air resistance is assumed to be zero).

However, the vertical components of velocity \((u \sin \theta)\) decreases continuously with height from \(O\) to \(A\), due to downward force of gravity and becomes zero at highest point \(A\). At this point, the object attains maximum height, now it has only horizontal component of velocity. From point \(A\), the object starts to fall down and reaches at point \(B\) on the ground.

Equation of path of projectile

\(y\) is the vertical distance travelled by object in time \(t\).

Motion along horizontal direction

The velocity of the object in horizontal direction, i.e. along \(O X\) is constant, so the acceleration \(a_x\) in horizontal direction is zero.
\(\therefore\) Position of the object at time \(t\) along horizontal direction is given by, \(x=x_0+u_x t+\frac{1}{2} a_x t^2\)
But \(x_0=0, u_x=u \cos \theta, a_x=0\) and \(t=t\)
\(\therefore \quad x=u \cos \theta t\)
\(
\text { Time, } t=\frac{x}{u \cos \theta} \dots(i)
\)

Motion along vertical direction (Equation of trajectory of projectile)

The vertical component of velocity of the object is decreasing from \(O\) to \(A\) due to gravity, so acceleration \(a_y\) is \(-g\).
\(\therefore\) Position of the object at any time \(t\) along the vertical direction, i.e. along \(O Y\) is given by, \(y=y_0+u_y t+\frac{1}{2} a_y t^2\)
But \(\quad y_0=0, u_y=u \sin \theta, a_y=-g\) and \(t=t\)
So, \(y=u \sin \theta t+\frac{1}{2}(-g) t^2=u \sin \theta t-\frac{1}{2} g t^2 \dots(ii)\)
Substituting the value of \(t\) from Eq. (i) in Eq. (ii), we get
\(
\begin{aligned}
y & =u \sin \theta\left(\frac{x}{u \cos \theta}\right)-\frac{1}{2} g\left(\frac{x}{u \cos \theta}\right)^2 \\
& =x \tan \theta-\frac{g}{2}\left(\frac{x}{u \cos \theta}\right)^2
\end{aligned}
\)
Vertical displacement, \(y=x \tan \theta-\left(\frac{1}{2} \frac{g}{u^2 \cos ^2 \theta}\right) x^2=x \tan \theta-\frac{g x^2}{2 u^2} \sec ^2 \theta\)
\(
y=x \tan \theta-\frac{g x^2}{2 u^2}\left(1+\tan ^2 \theta\right)
\)
This equation is in the form of \(y=a x-b x^2\), which represents a parabola and it is known as equation of trajectory of a projectile.

These are the standard equations of trajectory of a projectile. The equation is quadratic in \(x\). This is why the path of a projectile is a parabola. The above equation can also be written in terms of range \((R)\) of projectile as:
\(
y=x\left(1-\frac{x}{R}\right) \tan \theta
\)

The coordinates and velocity components of the projectile at time \(t\) are

\(
\begin{array}{c}
x=s_x=u_x t=(u \cos \theta) t \\
y=s_y=u_y t+\frac{1}{2} a_y t^2 \\
=(u \sin \theta) t-\frac{1}{2} g t^2 \\
v_x=u_x=u \cos \theta \\
v_y=u_y+a_y t=u \sin \theta-g t
\end{array}
\)
Therefore, speed of projectile at time \(t\) is \(v=\sqrt{v_x^2+v_y^2}\) and the angle made by its velocity vector with positive \(x\)-axis is
\(
\theta=\tan ^{-1}\left(\frac{v_y}{v_x}\right)
\)

Example 10: \(\mathrm{A}\) body is projected with a velocity of \(20 \mathrm{~ms}^{-1}\) in a direction making an angle of \(60^{\circ}\) with the horizontal. Determine its (i) position after \(0.5 \mathrm{~s}\) and (ii) the velocity after \(0.5 \mathrm{~s}\).

Answer: Given, \(u=20 \mathrm{~ms}^{-1}, \theta=60^{\circ}, t=0.5 \mathrm{~s}\)
(i) Since, horizontal distance,
\(
x=(u \cos \theta) t=\left(20 \cos 60^{\circ}\right) \times 0.5=5 \mathrm{~m}
\)
Similarly, vertical distance,
\(
\begin{aligned}
y & =(u \sin \theta) t-\frac{1}{2} g t^2 \\
& =\left(20 \sin 60^{\circ}\right) \times 0.5-\frac{1}{2} \times 9.8 \times(0.5)^2 \Rightarrow y=7.43 \mathrm{~m}
\end{aligned}
\)
(ii) Velocity along horizontal direction,
\(
v_x=u \cos \theta=20 \cos 60^{\circ}=10 \mathrm{~ms}^{-1}
\)
Velocity along vertical direction,
\(
v_y=u \sin \theta-g t=20 \sin 60^{\circ}-9.8 \times 0.5=12.42 \mathrm{~ms}^{-1}
\)

Example 11: A stone is thrown with a speed of \(10 \mathrm{~ms}^{-1}\) at an angle of projection \(60^{\circ}\). Find its height above the point of projection when it is at a horizontal distance of \(3 \mathrm{~m}\) from the thrower? \(\left(\right.\) Take, \(\left.g=10 \mathrm{~ms}^{-2}\right)\).

Answer: Considering the equation of trajectory,
\(
y=\left(\tan \theta_0\right) x-\frac{g}{2\left(v_0^2 \cos ^2 \theta_0\right)} x^2
\)
Here, \(\theta_0=60^{\circ}, v_0=10 \mathrm{~ms}^{-1}, x=3 \mathrm{~m}\)
\(
\begin{aligned}
\therefore \quad y & =\left(\tan 60^{\circ}\right) \times 3-\frac{10}{2\left(100 \cos ^2 60^{\circ}\right)}(3)^2 \\
& =3 \sqrt{3}-\frac{9}{5}=\frac{15 \sqrt{3}-9}{5} \mathrm{~m}=3.396 \mathrm{~m}
\end{aligned}
\)

Time of Flight, Maximum Height and Horizontal Range of a Projectile

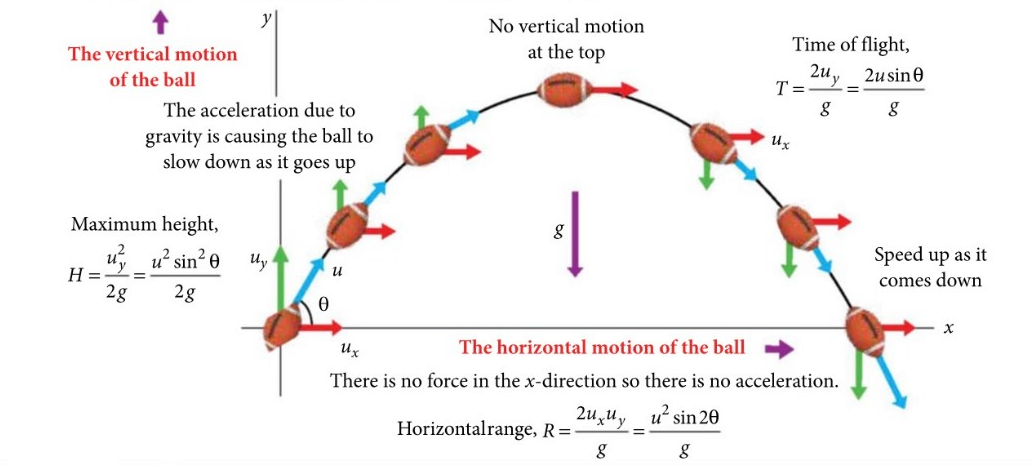
Figure below Shows a particle projected from the point \(O\) with an initial velocity \(u\) at an angle \(\theta\) with the horizontal. It goes through the highest point \(A\) and falls at \(B\) on the horizontal surface through \(O\). The point \(O\) is called the point of projection, the angle \(\theta\) is called the angle of projection, the distance \(O B\) is called the horizontal range \((\boldsymbol{R})\) or simply range and the vertical height \(A C\) is called the maximum height (H). The total time taken by the particle in describing the path \(O A B\) is called the time of flight \((T)\).

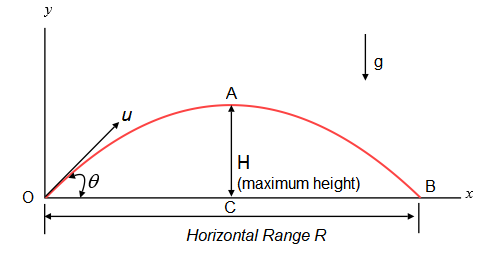
Time of flight of projectile [ T ]

It is defined as the total time for which projectile is in flight, i.e. time during the motion of projectile from \(O\) to \(B\). It is denoted by \(T\).
Time of flight consists of two parts such as
(i) Time taken by an object to go from point \(O\) to \(A\). It is also known as time of ascent \(\left(t_a\right)\).
(ii) Time taken by an object to go from point \(A\) to \(B\). It is also known as time of descent \(\left(t_d\right)\).
Total time can be expressed as
\(
T=t_a+t_d=2 t \quad \Rightarrow \quad t=T / 2 \quad\left(\because t_a=t_d=t\right)
\)
The vertical component of velocity of the projectile becomes zero at the highest point \(H\).
Let us consider vertical upward motion of the object from \(O\) to \(A\), we get
\(
u_y=u \sin \theta, a_y=-g, t=T / 2 \text { and } v_y=0
\)
Since, \(v_y=u_y+a_y t \Rightarrow 0=u \sin \theta-g \frac{T}{2}\)
\(\therefore \quad\) Time of flight, \(T=\frac{2 u \sin \theta}{g}\)

Example 12: A cricket ball is thrown at a speed of \(28 \mathrm{~ms}^{-1}\) in a direction \(30^{\circ}\) above the horizontal. Calculate the time taken by the ball to return to the same level.

Answer: Given, speed, \(u=28 \mathrm{~ms}^{-1}\) and \(\theta=30^{\circ}\)
\(\therefore\) The time taken by the ball to return the same level is
\(
T=\frac{2 u \sin \theta}{g}=\frac{2 \times 28 \times \sin 30^{\circ}}{9.8}=\frac{28}{9.8}=2.85 \simeq 2.9 \mathrm{~s}
\)

Maximum height of a projectile [ H ]

It is defined as the maximum vertical height attained by the projectile above the point of projection during its flight. It is denoted by \(H\).
Let us consider the vertical upward motion of the projectile from \(O\) to \(A\).
We have,
\(
\begin{array}{c}
u_y=u \sin \theta, a_y=-g, y_0=0, y=H, \\
t=\frac{T}{2}=\frac{u \sin \theta}{g}
\end{array}
\)
Using this relation, \(y=y_0+u_y t+\frac{1}{2} a_y t^2\)
We have, \(H=0+u \sin \theta\left(\frac{u \sin \theta}{g}\right)+\frac{1}{2}(-g)\left(\frac{u \sin \theta}{g}\right)^2\)
\(
=\frac{u^2}{g} \sin ^2 \theta-\frac{1}{2} \frac{u^2 \sin ^2 \theta}{g}
\)
Maximum height, \(H=\frac{u^2 \sin ^2 \theta}{2 g}\)

Example 13: Assume that a ball is kicked at an angle of \(60^{\circ}\) with the horizontal, so if the horizontal component of its velocity is \(19.6 \mathrm{~ms}^{-1}\), determine its maximum height.

Answer: Given,
\(
\theta=60^{\circ}
\)
Horizontal component of velocity \(=u \cos 60^{\circ}=19.6 \mathrm{~ms}^{-1}\)
\(
\therefore \quad u=\frac{19.6}{\cos 60^{\circ}}=\frac{19.6}{0.5}=39.2 \mathrm{~ms}^{-1}
\)
Therefore, maximum height,
\(
H=\frac{u^2 \sin ^2 60^{\circ}}{2 g}=\frac{(39.2)^2}{2 \times 9.8} \times\left(\frac{\sqrt{3}}{2}\right)^2=58.8 \mathrm{~m}
\)

Horizontal range of a projectile [ R ]

The horizontal range of a projectile is defined as the horizontal distance covered by the projectile during its time of flight. It is denoted by \(R\).
If the object having uniform velocity \(u \cos \theta\) (i.e. horizontal component) and the time of flight is \(T\), then the horizontal range covered by the projectile.
i.e. \(O B=R=u \cos \theta \times T=u \cos \theta \times 2 u \frac{\sin \theta}{g}\)
Horizontal range, \(R=\frac{u^2 \sin 2 \theta}{g} \quad(\because \sin 2 \theta=2 \sin \theta \cos \theta)\)
The horizontal range will be maximum, if angle of projection is \(45^{\circ}\).
\(\therefore\) Maximum horizontal range, \(R_{\max }=\frac{u^2}{g}\)
For same value of initial velocity, horizontal range of projectile is same for complementary angles.
So,
\(
R_{30^{\circ}}=R_{60^{\circ}} \text { or } R_{20^{\circ}}=R_{70^{\circ}}
\)

Important points about Projectile:

• A particle thrown in the space which moves under the effect of gravity only is called a projectile.
• Projectile motion is the combination of two motions.
• Projectile Motion = Horizontal Motion + Vertical Motion

Some important points related to projectile motion

(i) Velocity of the projectile at any instant \(t\),
\(
\begin{aligned}
\mathbf{v} & =v_x \hat{\mathbf{i}}+v_y \hat{\mathbf{j}}=u \cos \theta \hat{\mathbf{i}}+(u \sin \theta-g t) \hat{\mathbf{j}} \\
|\mathbf{v}| & =\sqrt{u^2+g^2 t^2-2 u g t \sin \theta}
\end{aligned}
\)

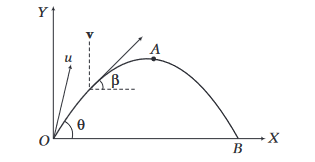
• This velocity makes an angle \(\beta\) with the horizontal given by
  \(
  \tan \beta=\frac{v_y}{v_x}=\frac{u \sin \theta-g t}{u \cos \theta} \dots(i)
  \)
• When the projectile reaches at point \(B\), substitute \(t=T\) in Eq. (i).

(ii) When a projectile is thrown upward, its kinetic energy decreases, potential energy increases but the total energy always remains constant.
(iii) Total energy of projectile \(=\) Kinetic energy + Potential energy
\(=\frac{1}{2} m v^2 \cos ^2 \theta+\frac{1}{2} m v^2 \sin ^2 \theta=\frac{1}{2} m v^2\)
(iv) In projectile motion, speed (and hence, kinetic energy) is minimum at highest point of its trajectory and given as
Speed \(=(\cos \theta)\) times the speed of projection and kinetic energy \(=\left(\cos ^2 \theta\right)\) times the initial kinetic energy.
Here, \(\theta=\) angle of projection.
(v) In projectile motion, it is sometimes better to write the equations of \(H, R\) and \(T\) in terms of \(u_x\) and \(u_y\) as
\(
\begin{aligned}
T & =\frac{2 u_y}{g}, H=\frac{u_y^2}{2 g} \\
\text { and } \quad R & =\frac{2 u_x u_y}{g}
\end{aligned}
\)
(vi) In projectile motion \(H=R\), when \(u_y=4 u_x\) or \(\tan \theta=4\)
(vii) Equation of trajectory can also be written as
\(
y=x\left(1-\frac{x}{R}\right) \tan \theta
\)
where, \(R\) is horizontal range.
(viii) All the above expressions for \(T, H\) and \(R\) are derived by neglecting air resistance. If air resistance is considered, then values may differ slightly.
(ix) Due to air resistance when a net speed of projectile decreases, then \(R\) decreases, \(T\) increases and \(H\) decreases. Reverse is the case when net speed increases.

Example 14: An object is projected with a velocity of \(30 \mathrm{~ms}^{-1}\) at an angle of \(60^{\circ}\) with the horizontal. Determine the horizontal range covered by the object.

Answer: Given, initial velocity, \(u=30 \mathrm{~ms}^{-1}\)
Angle of projection, \(\theta=60^{\circ}\)
Therefore, the horizontal range (or distance) covered by the object will be given as
\(
\begin{aligned}
R & =\frac{u^2 \sin 2 \theta}{g}=\frac{(30)^2 \sin 2\left(60^{\circ}\right)}{g} \\
& =\frac{(30)^2 2 \sin 60^{\circ} \cos 60^{\circ}}{9.8} \\
& =79.53 \mathrm{~m} \\
\Rightarrow \quad R & =79.53 \mathrm{~m}
\end{aligned}
\)

Example 15: A projectile has a range of \(40 \mathrm{~m}\) and reaches a maximum height of \(10 \mathrm{~m}\). Find the angle at which the projectile is fired.

Answer: Range of a projectile, \(R=\frac{u_0^2 \sin 2 \theta_0}{g}=40 \mathrm{~m} \dots(i)\)
\(
H=\frac{u_0^2 \sin ^2 \theta_0}{2 g}=10 \mathrm{~m} \dots(ii)
\)
On dividing Eq. (i) by Eq. (ii), we get
\(
\begin{aligned}
\frac{2\left(\sin 2 \theta_0\right)}{\sin ^2 \theta_0} & =4 \\
\frac{4 \sin \theta_0 \cos \theta_0}{\sin ^2 \theta_0} & =4
\end{aligned}
\)
\(
\begin{aligned}
\tan \theta_0 & =1 \\
\theta_0 & =45^{\circ}
\end{aligned}
\)

Example 16: Find the angle of projection of a projectile for which the horizontal range and maximum height are equal.

Answer: Given,
\(\therefore \quad \frac{u^2 \sin 2 \theta}{g}=\frac{u^2 \sin ^2 \theta}{2 g}\)
\(\quad 2 \sin \theta \cos \theta=\frac{\sin ^2 \theta}{2}\)
\(
\frac{\sin \theta}{\cos \theta}=4 \text { or } \tan \theta=4
\)
\(
\therefore \quad \theta=\tan ^{-1}(4)
\)

Example 17: There are two angles of projection for which the horizontal range is the same. Show that the sum of the maximum heights for these two angles is independent of the angle of projection.

Answer: Let the angles of projection be \(\alpha\) and \(90^{\circ}-\alpha\) for which the horizontal range \(R\) is same.
Now,
\(
H_1=\frac{u^2 \sin ^2 \theta}{2 g}
\)
and
\(
H_2=\frac{u^2 \sin ^2\left(90^{\circ}-\theta\right)}{2 g}=\frac{u^2 \cos ^2 \theta}{2 g}
\)
Therefore, \(H_1+H_2=\frac{u^2}{2 g}\left(\sin ^2 \theta+\cos ^2 \theta\right)=\frac{u^2}{2 g}\)
Clearly, the sum of the heights for the two angles of projection is independent of the values of projection angles.

Example 18: Prove that the maximum horizontal range is four times the maximum height attained by the projectile; when fired at an inclination so as to have maximum horizontal range.

Answer: For \(\theta=45^{\circ}\), the horizontal range is maximum and is given by
\(
R_{\max }=\frac{u^2}{g}
\)
Maximum height attained,
\(
H_{\max }=\frac{u^2 \sin ^2 45^{\circ}}{2 g}=\frac{u^2}{4 g}=\frac{R_{\max }}{4}
\)
\(
R_{\text {max }}=4 H_{\text {max }}
\)

Projectile fired at an angle with the vertical

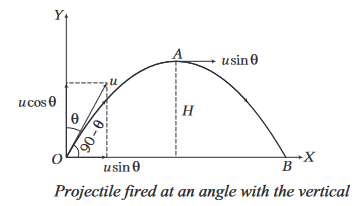
Let a particle be projected vertically with an angle \(\theta\) with vertical and it’s speed of projection is \(u\). Clearly, the angle made by the velocity of projectile at point of projection with horizontal is \(\left(90^{\circ}-\theta\right)\).
In this case
(i) Time of flight \(=\frac{2 u \sin \left(90^{\circ}-\theta\right)}{g}=\frac{2 u}{g} \cos \theta\)
(ii) Maximum height \(=\frac{u^2 \sin ^2\left(90^{\circ}-\theta\right)}{2 g}=\frac{u^2 \cos ^2 \theta}{2 g}\)
(iii) Horizontal range
\(
=\frac{u^2}{g} \sin 2\left(90^{\circ}-\theta\right)=\frac{u^2}{g} \sin \left(180^{\circ}-2 \theta\right)=\frac{u^2}{g} \sin 2 \theta
\)
(iv) Equation of path of projectile,
\(
\begin{aligned}
y & =x \tan \left(90^{\circ}-\theta\right)-\frac{1}{2} \frac{g x^2}{u^2 \cos ^2\left(90^{\circ}-\theta\right)} \\
& =x \cot \theta-\frac{g x^2}{2 u^2 \sin ^2 \theta}
\end{aligned}
\)
(v) Velocity at any time \(t\),
\(
\begin{aligned}
v & =\sqrt{u^2+g^2 t^2-2 u g t \sin \left(90^{\circ}-\theta\right)} \\
& =\sqrt{u^2+g^2 t^2-2 u g t \cos \theta}
\end{aligned}
\)
This velocity makes an angle \(\beta\) with the horizontal direction, then
\(
\tan \beta=\frac{u \sin \left(90^{\circ}-\theta\right)-g t}{u \cos \left(90^{\circ}-\theta\right)}=\frac{u \cos \theta-g t}{u \sin \theta}
\)

Example 19: A football is kicked at an angle of \(30^{\circ}\) with the vertical, so if the horizontal component of its velocity is \(20 \mathrm{~ms}^{-1}\), determine its maximum height.

Answer: Given, \(\theta=30^{\circ}\)
Horizontal component of velocity \(=u \sin 30^{\circ}=20 \mathrm{~ms}^{-1}\)
\(
\Rightarrow \quad u=\frac{20}{\sin 30^{\circ}}=\frac{20}{1 / 2}=40 \mathrm{~ms}^{-1}
\)
Therefore, maximum height,
\(
H=\frac{u^2 \cos ^2 30^{\circ}}{2 g}=\frac{(40)^2}{2 \times 9.8} \times\left(\frac{\sqrt{3}}{2}\right)^2=61.22 \mathrm{~m}
\)

Projectile from a Point Above the Ground

Projectile projected from a tower

When an object is at some height above the ground, then its projectile motion depends on the angle of projection.

Projectile projected horizontally from a tower

Assume that an object is thrown horizontally with some velocity \(u\) from point \(O\), on a tower of height \(h\) above the ground level and after time \(t\), it reaches ground at point E.

\(
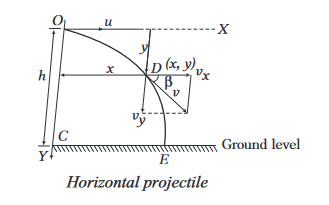
\begin{array}{cc}
\hline \text { Horizontal components } & \text { Vertical components } \\
\hline u_x=u & u_y=0 \\
\hline a_x=0\left(\because F_x=0\right) & a_y=-g \\
\hline
\end{array}
\)

Different terms related to this type of projectile motion are
(i) Equation of trajectory, \(y=\frac{1}{2}\left(\frac{g}{u^2}\right) x^2\)
(ii) Time of flight, \(T=\sqrt{\frac{2 h}{g}}\)
(iii) Horizontal range, \(R=u \sqrt{\frac{2 h}{g}}\)
(iv) Velocity of projectile at any instant,
\(
v=\sqrt{u^2+g^2 t^2}
\)

Example 20: A bomb is released from an aeroplane flying at a speed of \(720 \mathrm{kmh}^{-1}\) in the horizontal direction \(8000 \mathrm{~m}\) above the ground. At what horizontal distance from the initial position of aeroplane, it strikes the ground?

Answer:

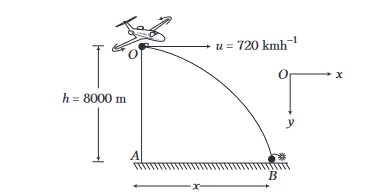
According to the figure, during motion of the bomb from \(O\) to \(B\),
\(
\begin{array}{rlrl}
& u =720 \times \frac{5}{18}=200 \mathrm{~ms}^{-1} \Rightarrow y=h=\frac{1}{2} g t^2 \\
\Rightarrow & 8000 =\frac{1}{2} \times 10 t^2 \Rightarrow t=40 \mathrm{~s} \\
\therefore & x =u t=200 \times 40=8000 \mathrm{~m}
\end{array}
\)

Example 21: A body is thrown horizontally from the top of a tower and strikes the ground after three seconds at an angle of \(45^{\circ}\) with the horizontal. Then, find
(i) the height of the tower.
(ii) the speed of projection of the body.

Answer: (i) Let \(H\) be the height of the tower.
The time of flight, \(T_f=\sqrt{\frac{2 H}{g}}=3 \mathrm{~s}\)
\(
\Rightarrow \quad H=\frac{g \times(3)^2}{2}=\frac{9.8 \times 9}{2}=44.1 \mathrm{~m}
\)
(ii) Let the speed of projection be \(v_0\).
Then, for horizontal projection,
\(
\begin{aligned}
v_x & =v_0 \Rightarrow v_y=-g t \\
\text { At } \quad t & =T_f=3 \mathrm{~s}, v_y=-9.8 \times 3=-29.4 \mathrm{~ms}^{-1}
\end{aligned}
\)
The angle which the final velocity makes with the horizontal \(=\boldsymbol{\theta}=45^{\circ}\)
(Given)
\(
\Rightarrow \quad \tan 45^{\circ}=\frac{-v_y}{v_x} \Rightarrow-v_y=v_x
\)
So,
\(
v_x=29.4 \mathrm{~ms}^{-1}
\)

Example 22: A projectile is fired horizontally with a velocity of \(98 \mathrm{~ms}^{-1}\) from the top of a hill \(490 \mathrm{~m}\) high. Find
(i) the time taken by the projectile to reach the ground,
(ii) the distance of the point, where the particle hits the ground from foot of the hill and
(iii) the velocity with which the projectile hits the ground. \(\left(\right.\) Take, \(g=9.8 \mathrm{~ms}^{-2}\) )

In this problem, we cannot apply the formulae of \(R, H\) and \(T\) directly. Here, it will be more convenient to choose \(x\) and \(y\) directions as shown in figure.
Here, \(u_x=98 \mathrm{~ms}^{-1}, a_x=0, u_y=0\) and \(a_y=g\).
(i) At \(A, s_y=490 \mathrm{~m}\). So, applying
\(
\begin{aligned}
& s_y=u_y t+\frac{1}{2} a_y t^2 \\
\Rightarrow \quad & 490=0+\frac{1}{2}(9.8) t^2 \quad \therefore t=10 \mathrm{~s}
\end{aligned}
\)
(ii) \(B A=s_x=u_x t+\frac{1}{2} a_x t^2\) or \(B A=(98)(10)+0\left(\because a_x=0\right)\) or \(B A=980 \mathrm{~m}\)
(ii) \(B A=s_x=u_x t+\frac{1}{2} a_x t^2\) or \(B A=(98)(10)+0\left(\because a_x=0\right)\) or \(B A=980 \mathrm{~m}\)
(iii) Horizontal velocity, \(v_x=u_x=98 \mathrm{~ms}^{-1}\)
Vertical velocity, \(v_y=u_y+a_y t=0+(9.8)(10)=98 \mathrm{~ms}^{-1}\)
\(\therefore\) Resultant velocity, \(v=\sqrt{v_x^2+v_y^2}=\sqrt{(98)^2+(98)^2}\)
\(
=98 \sqrt{2} \mathrm{~ms}^{-1}
\)
and \(\quad \tan \beta=\frac{v_y}{v_x}=\frac{98}{98}=1 \quad \therefore \beta=45^{\circ}\)
Thus, the projectile hits the ground with a velocity \(98 \sqrt{2} \mathrm{~ms}^{-1}\) at an angle of \(\beta=45^{\circ}\) with horizontal as shown in the given figure.

Projectile projected upward from a tower

Consider a projectile projected upward at an angle \((\boldsymbol{\theta})\) from point \(O\) which is situated on a tower at height \(h\) above the ground. Now, from the diagram, we have
\(
\begin{array}{l}
u_x=u \cos \theta, a_x=0 \\
u_y=u \sin \theta, a_y=-g
\end{array}
\)
(i) Equation of horizontal motion, \(x=u \cos \theta t \dots(i)\)
(ii) Equation of vertical motion,
\(
-h=u \sin \theta t-\frac{1}{2} g t^2 \dots(ii)
\)

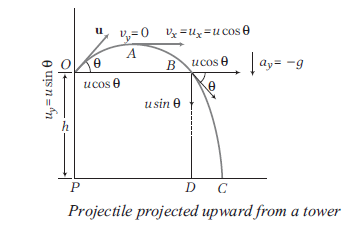
(iii) Time of flight, \(T=\frac{u \sin \theta}{g} \pm \sqrt{\frac{u^2 \sin ^2 \theta}{g^2}+\frac{2 h}{g}}\)
(iv) Horizontal distance covered (in time of flight T),
\(
P C=(u \cos \theta) T
\)
(v) Horizontal distance covered from the top of tower,
\(
O B=\frac{u^2 \sin 2 \theta}{g}
\)
In such case for range \(P C\) to become maximum, \(\theta\) should be \(45^{\circ}\).

Example 23: A boy playing on the roof of a \(10 \mathrm{~m}\) high building throws a ball with a speed of \(10 \mathrm{~ms}^{-1}\) at an angle of \(30^{\circ}\) with the horizontal. How far from the throwing point will the ball be at the height of \(10 \mathrm{~m}\) from the ground?

Answer: The ball will be at point \(P\) when it is at a height of \(10 \mathrm{~m}\) from the ground. So, we have to find distance \(O P\), which can be calculated by direct considering it, as a projectile on a level \(O X\) at a height \(h\) from the horizontal level.

\(
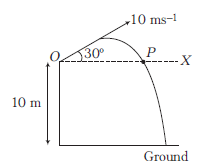
\begin{array}{l}
O P=R=\frac{u^2 \sin 2 \theta}{g} \\
R=\frac{10^2 \times \sin \left(2 \times 30^{\circ}\right)}{10}=8.66 \mathrm{~m}
\end{array}
\)

Projectile projected downward from a tower

Consider a projectile projected downward at an angle \(\theta\) from point \(O\) which is on a tower of height \(h\) above the ground.
Now, from the diagram, we have
\(
\Rightarrow \quad \begin{array}{l}
u_x=u \cos \theta, a_x=0 \\
u_y=-u \sin \theta, a_y=-g
\end{array}
\)

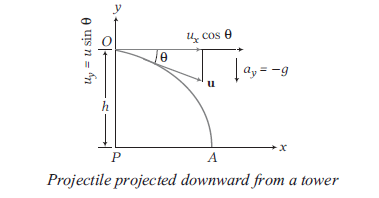
(i) Equation of motion, \(-h=(-u \sin \theta) t+\frac{1}{2}(-g) t^2\) or
\(
g t^2+(2 u \sin \theta) t-2 h=0
\)
(ii) Time of flight, \(T=\frac{-2 u \sin \theta}{2 g} \pm \frac{\sqrt{4 u^2 \sin ^2 \theta+8 g h}}{2 g}\)
(iii) Horizontal distance covered from the base of tower,
\(
P A=(u \cos \theta) T
\)

Example 24: A boy standing on the top of a tower \(36 \mathrm{~m}\) high has to throw a packet to his friend standing on the ground \(48 \mathrm{~m}\) horizontally away. If he throws a packet directly aiming the friend with a speed of \(10 \mathrm{~ms}^{-1}\), how short will the packet fall?

Answer: The packet will strike at point \(C\) instead of reaching to point \(B\) because the packet will move in a parabolic path instead of straight line.

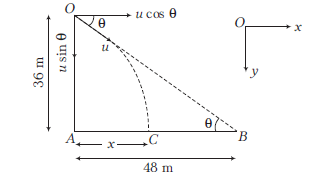
From geometry, \(\tan \theta=\frac{36}{48}=\frac{3}{4}\) \(\Rightarrow \quad \sin \theta=\frac{3}{5}, \cos \theta=\frac{4}{5}\)
For \(O\) to \(C, s_y=u \sin \theta t+\frac{1}{2} g t^2\)
\(
36=10 \times \frac{3}{5} t+\frac{1}{2} \times 10 t^2=6 t+5 t^2
\)
\(
\begin{aligned}
5 t^2+6 t & -36=0 \\
t & =2.15 \mathrm{~s}, \\
s_x & =u \cos \theta t=10 \times \frac{4}{5} \times 2.15 \\
& =17.2 \mathrm{~m}=A C \\
B C & =A B-A C=48-17.2=30.8 \mathrm{~m}
\end{aligned}
\)
The packet will fall at distance \(30.8 \mathrm{~m}\) in front of his friend.