Prime Numbers
What are Prime Numbers?
Prime numbers are numbers greater than 1. They only have two factors, 1 and the number itself. This means these numbers cannot be divided by any number other than 1 and the number itself without leaving a remainder. The first ten primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Note: It should be noted that 1 is a non-prime number. It is a unique number. According to the definition of the prime number, which states that a number should have exactly two factors for it to be considered a prime number. But, number 1 has one and only one factor which is 1 itself. Thus, 1 is not considered a Prime number.
Numbers that have more than 2 factors are known as composite numbers.
Note: Prime numbers are the natural numbers greater than 1 with exactly two factors, i.e. 1 and the number itself.
Let’s look at the examples given below.
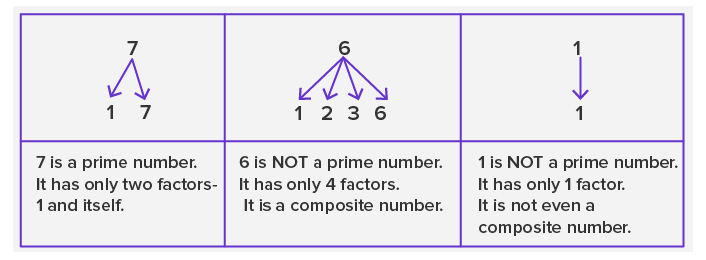
Difference between Prime Number and Composite Number
\(\begin{array}{|l|l|}
\hline {\text { Prime Number }} & {\text { Composite Number }} \\
\hline \text { A prime number has two factors. } & \begin{array}{l}
\text { A composite number has more } \\
\text { than two factors. }
\end{array} \\
\hline \begin{array}{l}
\text { A prime number is divided by } 1 \text { and the } \\
\text { number itself. } \\
\text { For example: } 3 \text { is divisible by } 1 \text { and } 3 .
\end{array} & \begin{array}{l}
\text { A composite number is divided by all } \\
\text { its factors. } \\
\text { For example: } 12 \text { is divisible by } \\
1,2,3,4,6,12 .
\end{array} \\
\hline \text { Examples: } 2,3,5,7,11 \text {, etc. } & \text { Examples: } 4,6,8,9 \text {, etc. } \\
\hline
\end{array}
\)
The Sieve of Eratosthenes
In the third century BCE, the Greek mathematician Eratosthenes found a very simple method of finding the prime numbers. Follow the below-given steps to identify the prime numbers between 1 and 100.
- Step 1: Make a hundred charts.
- Step 2: Leave 1 as it is neither a prime number nor a composite number.
- Step 3: Encircle 2 and cross out all its multiples as they are not prime.
- Step 4: Encircle the next uncrossed number, which is 3, and cross out all its multiples. Ignore the previously crossed-out numbers like 6,12,18, and so on.
- Step 5: Continue the process of encircling the next uncrossed number and crossing out its multiples till all the numbers in the table are either encircled or crossed out, except 1.
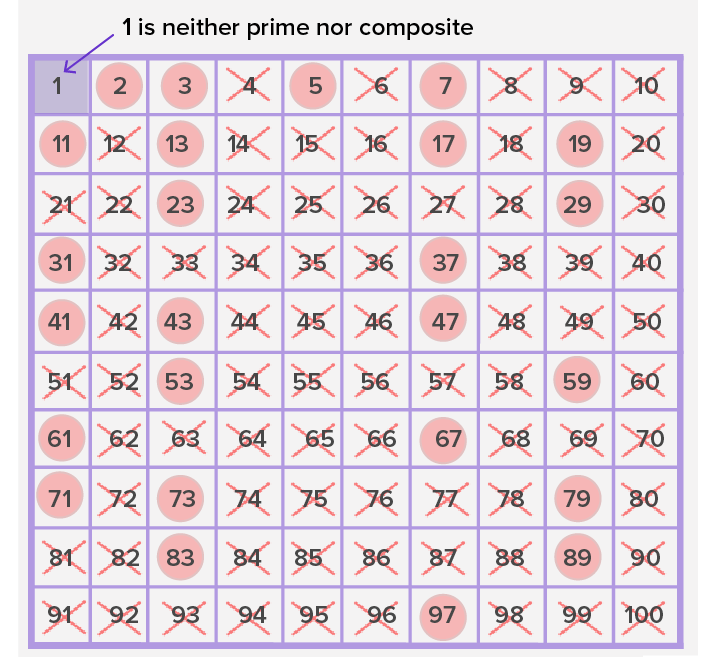
So, from the table, it is clear that 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 are the prime numbers. There are 25 prime numbers between 1 and 100.
Terms Related to Prime Numbers
Co-Primes: Two numbers are said to be co-prime if they have only one common factor, that is, 1. It is not necessary for these numbers to be prime numbers. For example, 9 and 10 are co-primes. Let’s verify.
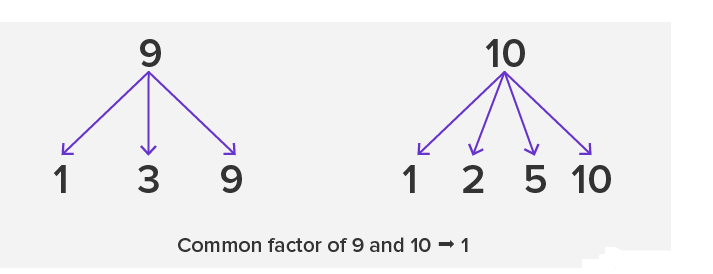
Note that pairs of any 2 prime numbers are always co-primes. This is because, out of their two factors, the common factor can only be 1. So, (3, 5), (11, 19) are some examples of co-primes.
What are Co-Prime Numbers?
Suppose \(x\) and \(y\) are two positive integers such that they are called co prime numbers if and only if they have 1 as their only common factor and thus \(\operatorname{HCF}(x, y)=1\). In other words, Co-prime numbers are a set of numbers or integers which have only 1 as their common factor i.e. their highest common factor (HCF) will be 1. Co-prime numbers are also known as relatively prime or mutually prime numbers. It is important that there should be two numbers in order to form co-primes.
How to Find Co-prime Numbers?
Consider a set of two numbers, if they have no positive integer that can divide both, other than 1 , the pair of numbers is co-prime.
Example 1: Are 21 and 22 co-prime numbers?
Solution:
For 21 and 22:
The factors of 21 are \(1,3,7\), and 21.
The factors of 22 are \(1,2,11\), and 22 .
Here 21 and 22 have only one common factor which is 1 . Hence, their HCF is 1, and are co-prime.
Example 2: Are 21 and 27 co-prime numbers?
Solution:
For 21 and 27 :
The factors of 21 are \(1,3,7\), and 21 .
The factors of 27 are \(1,3,9\), and 27 .
Here 21 and 27 have two common factors; they are 1 and 3 . HCF is 3 and they are not co-prime.
Twin-Primes: The prime numbers with only one composite number between them are called twin prime numbers or twin primes. The other definition of twin prime numbers is the pair of prime numbers that differ by 2 only. For example, 3 and 5 are twin primes because 5 – 3 = 2.
The other examples of twin prime numbers are:
- (5, 7) [7 – 5 = 2]
- (11, 13) [13 – 11 = 2]
- (17, 19) [19 – 17 = 2]
- (29, 31) [31 – 29 = 2]
- (41, 43) [43 – 41 = 2]
- (59, 61) [61 – 59 = 2]
- (71, 73) [73 – 71 = 2]
Some Facts about Prime Numbers
- 2 is the smallest prime number.
- 2 is the only prime number that is even and the rest of the prime numbers are odd numbers.
- 2 and 3 are the only consecutive prime numbers.
- Except for 0 and 1, a whole number is either a prime number or a composite number.
- All odd numbers are not prime numbers. For example, 21, 39, etc.
- No prime number greater than 5 ends in a 5.
- Sieve of Eratosthenes is one of the earliest methods of finding prime numbers.
- Prime numbers get rarer as the number gets bigger.
- There is no largest prime number. The largest known prime number (as of September 2021) is 282,589,933 − 1, a number that has 24,862,048 digits when written in base 10. By the time you read this, it may be even larger.
Formula to Find Prime Numbers
- The prime number formula helps in checking whether the given number is prime or not. Also, the formula helps us to generate a random prime number. We can write a prime number greater than 3 in the form of \(6 n+1\) or \(6 n-1\).
- This method excludes the numbers that are multiples of prime numbers. To generate the prime number greater than 40, we use the formula \(n^2+n+41\) where \(n\) can take the values from 0 till 39.
Method 1: Every prime number, apart from 2 and 3 , can be written in the form of \(6 n+1\) or \(6 n-1\). So, if we have any number different from 2 and 3 , we can check if it is prime or not by trying to express it in the form of \(6 n+1\) or \(6 n-1\)
- Let us check this formula, \(6 n-1\) , for the number 1 , So, 6(1) – \(1=5\)
- Let us check this formula, \(6 n+1\) for the number 01, So, \(6(1)+1=7\)
- Let us check this formula, \(6 n-1\) , for the number 0, So, \(6(2)-1=11\)
- Let us check this formula, \(6 n+1\) , for the number 0, So, \(6(2)+1=13\)
Now, we know that the numbers \(5,7,11\), and 13 are prime.
Method 2: Substitute whole numbers for \({n}\) in the formula ‘ \({n}^{{2}} {+} {n}+{4 1}\) ‘.
This formula will give you all the prime numbers greater than 40. Let us substitute a few whole numbers and check.
- Let us check this formula, \({n}^{{2}} {+} {n}+{4 1}\), for the number 0 , So, \({0}^2+0+\) \(41=0+41=41\)
- Let us check this formula, \({n}^{{2}} {+} {n}+{4 1}\), for the number 1 , So, \(1^2+1+41\) \(=2+41=43\)
- Let us check this formula, \({n}^{{2}} {+} {n}+{4 1}\), for the number 2 , So, \(2^2+2+41\) \(=6+41=47\)
Therefore, we can calculate all the prime numbers greater than 40 using this formula.
Rules for Prime Number Formula
Below are some rules that have to be followed when dealing with prime number and prime number formulas.
- If the digit at the unit’s place is even, then the number cannot be a prime number.
- Of all the prime numbers, 2 is the only even prime number.
- A prime number greater than 3 can be written in the form of \(6 n+1\) or \(6 n-1\).
Example 3: Is 57 a Prime Number?
Solution:
By the division method, we find that \(1,3,19\), and 57 divide 57.
For a number to be a prime number, a number should have only 2 factors, i.e., 1 and the number itself. We can see that 57 has more than 2 factors. Therefore, 57 is not a prime number.
Also, 57 could not be represented in the form of \(6 n+1\) where \(n=1,2,3 \ldots\)
Therefore, 57 is not a prime number.
Example 4: Find out whether 79 is a prime number or not with the help of the prime number formula.
Solution: With the help of the division method, we find that 1 and 79 divide 79 completely.
No other number divides 79 completely. Thus, 79 has only 2 factors.
Also, if we divide 79 by 6, we get the remainder as 1.
Thus we can represent it as \(6 n+1: 6 \times 13+1=78+1=79\)
Therefore, 79 is a prime number.
Example 5: Check if the number 29 is a prime number or not using the prime numbers formula.
Solution: The factors of 29 are 29 and 1.
Let us check if 29 can be represented using the prime numbers formula: \(6 n-1\)
Divide 29 by 6.
We can represent 29 as \(6 \times 5-1\)
Therefore, 29 is a prime number.