Permutation is about making arrangements in which order matters. For example, the combination to the safe is 452. Now we do care about the order. If we use 524 or 245 to open the safe it won’t work. It has to be exactly 452.

Note: Therefore when the order does matter it is a permutation.

There are basically two types of permutation:

1. Repetition is Allowed: such as the lock above. It could be “555”.
2. No Repetition: for example the first three people in a running race. You can’t be first and second.

Permutation with Repetition

The number of permutations of \(n\) different things taken \(r\) at a time, when repetition is allowed is \(n^r\).

Explanation: These are the easiest to calculate.
When a thing has \({n}\) different types … we have \({n}\) choices each time!
For example: choosing 3 of those things, the permutations are:
\(
\begin{gathered}
{n} \times {n} \times {n} \\
\text { (n multiplied } 3 \text { times) }
\end{gathered}
\)
More generally: choosing \({r}\) of something that has \({n}\) different types, the permutations are:
\(
n \times n \times \ldots(r \text { times })
\)
(In other words, there are \({n}\) possibilities for the first choice, Then there are \({n}\) possibilities for the second choice, and so on, multiplying each time.)
Which is easier to write down using an exponent of \({r}\) :
\(
P(n,r)={n} \times {n} \times \ldots({r} \text { times })={n}^{{r}}
\)

Notice that the base (\({n}\)) is the total number of objects in the set, and the exponent (\({r}\)) is the number of objects being selected.

Example 1: How many 3-letter words with or without meaning can be formed out of the letters of the word SPIKE when repetition of words is allowed?

Solution: 

The number of objects, in this case, is 5, as the word SPIKE has 5 alphabets. and \(r=3\), as 3-letter word has to be chosen. Thus, the permutation will be:
Permutation (when repetition is allowed) \(=5^3=125\)

Example 2:  A spinner is divided into four equally sized quadrants of different colors: red, yellow, green, and blue. You spin the spinner three times, recording the color that results from each spin. How many possible permutations exist for the colored spins?

Solution:

This is an example of finding permutations with repetition because the spinner can land on the same color multiple times. That means we need to use the formula \(P=n^r\)
In this case, \(\mathrm{n}\) is 4 because there are four colors, and \(\mathrm{r}\) is 3 because the spinner is being spun 3 times. Therefore:
\(P=4^3=64\)
So the total number of permutations is 64.

Example 3: How many 3-letters can be selected from the 26 alphabets (assuming repetition is allowed).

Solution:

For instance, if three letters from the alphabets \(A\) to \(Z\) were to be selected, then the letter A can be selected in those 3 times like AAA. The same argument goes for \(B\) and \(C\) and so on etc. Since we have 26 alphabets, we have 26 choices each time. Therefore, the amount of times the three letters would be selected is,
\(26^3=17576 \text { times }\)
where the base 26 means that there are 26 alphabets and the exponent 3 represents the number of alphabets to be selected.

Example 4:  Given the set of numbers, 1, 2, and 3, how many ways can we choose two numbers?

Solution:

When a permutation can repeat, we just need to raise \(\mathrm{n}\) to the power of however many objects from n we are choosing, so \(n^r\)

where \(\mathrm{n}\) is the number of distinct objects in a set, and \(\mathrm{r}\) is the number of objects chosen from set \(\mathrm{n}\).

In this given example given are the set of numbers, 1, 2, and 3. We need to find how many ways can we choose two numbers.

\(P(n, r)=P(3,2)=3^2=9\).

We can confirm this by listing all the possibilities:
\(
\begin{array}{lll}
11 & 12 & 13 \\
21 & 22 & 23 \\
31 & 32 & 33
\end{array}
\)

You can see we have only a total of 9 possibilities.

Example 5: How many 6-digit numbers can be formed using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 if repetitions of digits are allowed (remember that you can not have zero as the first digit)?

Solution:

There are 6 digits.  Each digit can take ten different numbers except for the first digit since it cannot be zero. if 0 is allowed as a starting digit, we have 000000 to \(999999 \rightarrow 1\) million combinations
However, if you disallow 0 as a starting digit then you have the following:

9 choices for the first digit \((1-9)\)
10 choices for the second digit \((0-9)\)
10 choices for the third digit \((0-9)\)
10 choices for the fourth digit \((0-9)\)
10 choices for the fifth digit \((0-9)\)
10 choices for the sixth digit \((0-9)\)
\(9 \times 10 \times 10 \times 10 \times 10 \times 10=900000\) combinations

Example 6: How many 3-letter words can be formed using the letters c,a,t allowing for repetition of the letters?

Solution:

There are 3 letters that can be used to fill the first location. Because repetition is allowed, the same 3 letters can be used to fill the second location and also the last location. Using the formula we can get

\(P(n, r)=P(3,3)=3^3=27\).

\(
\begin{aligned}
&27 \text { arrangements with repetition are shown below: }\\
&\begin{array}{lll}
\text { ccc } & \text { aaa } & \text { ttt } \\
\text { caa } & \text { acc } & \text { taa } \\
\text { ctt } & \text { att } & \text { tcc } \\
\text { cat } & \text { act } & \text { tac } \\
\text { cta } & \text { atc } & \text { tca } \\
\text { cac } & \text { aca } & \text { tct } \\
\text { ctc } & \text { ata } & \text { tat } \\
\text { cca } & \text { aac } & \text { ttc } \\
\text { cct } & \text { aat } & \text { tta }
\end{array}
\end{aligned}
\)

Example 7: How many 3-digit numbers greater than 500 can be formed using 3, 4, 5, and 7(repetition of digits allowed)?

Solution:

Since a three-digit number, greater than 500 will have either 5 or 7 at its hundredth place, we have 2 choices for this place. There is no restriction on the repetition of the digits, hence for the remaining 2 digits we have 4 choices each (33, 34, 43, 44).

So the total permutations are: 2 × 4 × 4 = 32

Example 8: How many even numbers lying between 1000 and 2000 can be formed using the digits 1, 2, 4, 5, and 9?

Solution: 

Since the number is supposed to be even, the digits at the unit place must either be 2 or 4 leaving us with 2 choices for the digit at the unit place.

The number is supposed to lie between 1000 and 2000, So the digits at the thousand’s place must be 1, we thus have 1 choice for the digit at the thousand’s place.

The rest of the 2 digits can be anyone from 1, 2, 4, 5, and 9 i.e. 5 choices each

So the total permutations are: 2 × 5 × 5 × 1 = 50

Example 9: A police officer visits the crime scene 3 times a week for investigation. Find the number of ways to schedule his visit if there is no restriction on the number of visits per day.

Solution:

The number of ways to schedule the first visit is 7 (any of the 7 days)
The number of ways to schedule a second visit is 7 (any of the 7 days)
The number of ways to schedule a third visit is 7 (any of the 7 days)
Hence, the number of ways to schedule the first and second, and third visit is \(7 \times 7 \times 7=7^3=343\)

Example 10: In how many ways can 6 prisoners be placed in 4 cells if any number of prisoners can fit in a cell?

Solution:

The \(1^{\text {st }}\) prisoner can be sent to any of the 4 cells
The \(2^{\text {nd }}\) prisoner can be sent to any of the 4 cells
The \(3^{\text {rd }}\) prisoner can be sent to any of the 4 cells
The \(4^{\text {th }}\) prisoner can be sent to any of the 4 cells
The \(5^{\text {th }}\) prisoner can be sent to any of the 4 cells
The \(6^{\text {th }}\) prisoner can be sent to any of the 4 cells
The total arrangements are:
\(4 \times 4 \times 4 \ldots(6 \text { times })=4^6\)

Permutation of Distinct Objects, without Repetition

The formula that is used to calculate the number of permutations is
\({ }^n P_r=P(n,r)=\frac{n !}{(n-r) !}\)
Here, \(n\) is the total number of objects, and \(r\) is the chosen objects.

In particular, when \(r=n,{ }^n P_n=\frac{n !}{(n-n) !}=\frac{n !}{0 !}=\frac{n !}{1}=n \text { ! } \). Therefore, the number of all permutations of \(n\) distinct objects, taken all at a time, is \( n \text { ! }\).

In this case, we have to reduce the number of available choices each time. Since there is no repetition of a member of a set used when making selections. Once a member is used, it cannot be reused and as such reduces the chances available.

For example, what order could 16 pool balls be in?

After choosing, say, the number “15” we can’t choose it again.
So, our first choice has 16 possibilities (1, 2, 3,…….,16), and our next choice has 15 possibilities, then \(14,13,12,11, \ldots\), etc.,

Therefore, the total permutations are:
\(
16 \times 15 \times 14 \times 13 \times \ldots=20,922,789,888,000
\)

But maybe we don’t want to choose them all if we just choose 3 of them, and that is then the total permutations are:
\(
16 \times 15 \times 14=3,360
\)
In other words, there are 3,360 different ways that 3 pool balls could be arranged out of 16 balls.

Another example, consider selecting an alphabet from a total of 26 alphabets.

For instance, if one alphabet is to be picked (out of 26 alphabets) and \(A\) is picked, once \(A\) is used it cannot be reused, reducing our chances from 26 to 25.
Likewise, if two alphabets are to be picked and you pick \(A\) and \(B\), once \(A\) and \(B\) are used, it further reduces our possibility from 26 to 24 and so on. Thus it leaves us with:
\(
\begin{aligned}
& 26 \times 25 \times 24 \times 23 \times 22 \times 21 \ldots \times 1=26 ! =403291461126605635584000000
\end{aligned}
\)
Therefore, unlike permutation with repetition which allows item among the sets to be replaced and reused, permutations without repetition does not allow the replacement and subsequent use of any item once used.

Example 11: Find the number of different 3-letter words that can be formed by the letters of the word NUMBER.

Solution:

\(
\begin{aligned}
& { }^n P_r=\frac{n !}{(n-r) !} \\
& { }^6 P_3=\frac{6 !}{(6-3) !} =\frac{6 !}{3 !} \\
& =\frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{3 \times 2 \times 1} \\
& =4 \times 5 \times 6 \\
& \therefore{ }^6 P_3=120
\end{aligned}
\)
Hence, we can have 120 different 3-letter words in this case (repetition is not allowed in this case).

Example 12: How many 4 -digit numbers can be formed by using the digits 1 to 9 if repetition of digits is not allowed?

Solution:

Since there are a total of 9 digits (1 to 9) required 4 digit numbers \(={ }^9 P_4=\frac{9 !}{(9-4) !}=\frac{9 !}{5 !}\)
\(
\begin{aligned}
& =\frac{9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{5 \times 4 \times 3 \times 2 \times 1} \\
& =9 \times 8 \times 7 \times 6=3024
\end{aligned}
\)

Example 13: How many distinct words can be made up by using all of the letters in the word ‘TRIANGLES’?

Solution:

There are 9 distinct letters in the word TRIANGLE. Thus, the number of different permutations of the letters of this word is,
\(
\begin{aligned}
& { }^9 P_9=\frac{9 !}{(9-9) !}=\frac{9 !}{0 !}=\frac{9 !}{1}=9!=362880
\end{aligned}
\)
Hence, the number of words is 362,880.

Example 14: How many 3-letter words can be made using the letters of the word ‘TRAPEZIUMS’, with or without meaning, if repetition of letters is not allowed?

Solution:

The word ‘TRAPEZIUMS’ has 10 different letters. So, the number of 3 letter words (with or without meaning) formed by using these letters
\(
\begin{aligned}
& { }^{10} P_3=\frac{10 !}{(10-3) !}=\frac{10 !}{7 !} \\
& =\frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1} \\
& =10 \times 9 \times 8 \\
& =720
\end{aligned}
\)

Example 15: How many words that start with T and end with L can be made from the word TRIANGLES?

Solution:

If we fix T at the start and L at the end of the word, those two spaces are not to be considered further. We just have to permute 7 distinct letters in 7 places.
\(
\begin{aligned}
& { }^7 P_7=\frac{7 !}{(7-7) !}=\frac{7 !}{0 !}=\frac{7 !}{1}=7!=5040
\end{aligned}
\)
Hence, the number of words is 5040.

Example 16: In a Casino Gambling company, the manager must select the top three goals of the month, from a list of ten goals. Find out in how many ways can the top three goals be decided.

Solution:

Since the manager must decide the top three goals of the month; the order of the goals is very important! Thus, the problem is of permutations.
When he picks up three goals from a list of ten:
Possible ways the top three goals be decided \(={ }^{10} P_3=\frac{10 !}{(10-3) !}=10 \times 9 \times 8=720\)
Hence, there are 720 ways of picking the top three goals.

Example 17: How many ways can first and second place be awarded to 10 students in a class?

Solution:

\(\frac{10 !}{(10-2) !}=\frac{10 !}{8 !}=\frac{3,628,800}{40,320}=90\) (which is just the same as: 10 × 9 = 90)

Explanation: 

Any of the students among 10 can win first place. Once the first place is taken second place can be taken by any of the remaining 9 students. This makes 10 x 9 = 90 ways students can take first and second place.

Example 18: Seven athletes are participating in a race. In how many ways can the first two prizes be won?

Solution:

Required number of ways
\(
\begin{aligned}
& ={ }^7 P_2=\frac{7 !}{(7-2) !}=\frac{7 !}{5 !}=\frac{7 \times 6 \times 5 !}{5 !}=42
\end{aligned}
\)

Example 19: In how many ways six children can be arranged in a line, such that, two particular children of them are always together?

Solution:

Given that two particular children need to be together, so we consider them as a single object. So we have a total of 5 objects now. Thus, the five objects, including the single object, can be arranged in 5! Ways i.e., 120.
Also, the two children can be arranged in 2 ! ways.
Hence, the total number of arrangements \(=5! \times 2 !=120 \times 2=240\) ways.

Example 20: How many 4-digit numbers are there with distinct digits?

Solution:

Total number of arrangements of ten digits \((0,1,2,3,4,5,6,7,8,9)\) taking 4 at a time \(={ }^{10} \mathrm{P}_4\)
These arrangements also have those numbers which have 0 at the thousand’s place.
(For example 0589 which is not a 4 -digit number.).
If we fix 0 at the thousand’s place, we need to arrange the remaining 9 digits by taking 3 at a time.
Total number of such arrangements \(={ }^9 P_3\)
Thus, the total number of 4-digit numbers \(={ }^{10} P_4-{ }^9 P_3\)

Example 21: How many different words can be formed with the letters of the word “COMPUTER” so that the word begins with “C”?

Solution:

Since all the words must begin with \(\mathrm{C}\). So, we need to fix the \(\mathrm{C}\) at the first place. The remaining 7 letters can be arranged in \({ }^7 P_7=7 !=5040\) ways.

Example 22: In how many ways can 8 ninth graders and 6 tenth graders be arranged for a group photograph if the tenth graders are to sit on chairs in a row and the ninth graders are to stand in a row behind them?

Solution:

6 tenth graders can sit on chairs in a row in \({ }^6 \mathrm{P}_6=6\)! ways
8 ninth graders can stand behind in a row in \({ }^8 \mathrm{P}_8=8\)! ways
Thus, the total number of ways
\(
=6 ! \times 8 ! \text { ways }
\)

Permutations When all Objects are not Distinct

Case-1: The number of permutations of \(n\) objects, where \(p\) objects are of the same kind and rest all are different \(=\frac{n !}{p !}\)

Case-2: The number of permutations of \(n\) objects, where \(p_1\) objects are of one kind, \(p_2\) objects are of the second kind, … \(p_k\) are of \(k^{t h}\) kind and the remaining all are of a different kind, is given by the formula:
\(
\frac{n !}{p_{1} ! p_{2} ! \ldots p_{k} !}
\)

Example 23: Find the number of ways of rearranging the letters of the word GOOD.

Solution:

In this case, the letters of the word are not all different. There are \(2 \mathrm{O’s}\), which are of the same kind. Let us treat, temporarily, the \(2 \mathrm{O’s}\) as different, say, \(\mathrm{O_1}\) and \(\mathrm{O_2}\). The number of permutations of 4 different letters, taken all at a time, is \(4 !\).

Consider one of these permutations, say, \(\mathrm{GO}_1 \mathrm{O}_2 \mathrm{~D}\). Corresponding to this, we have 2 ! permutations \(\mathrm{GO_1} \mathrm{O}_2 \mathrm{~D}\) and \(\mathrm{G O_2 O_1 D}\) which will be the same permutation if \(\mathrm{O_1}\) and \(\mathrm{O_2}\) are not considered as different, i.e., if \(\mathrm{O_1}\) and \(\mathrm{O_2}\) are the same \(\mathrm{O}\) at both places. Therefore, the required number of permutations \(=\frac{4 !}{2 !}=3 \times 4=12\)

Example 24: Find the number of permutations of the letters in the word ALLAHABAD.

Solution:

The word ALLAHABAD has 9 letters or objects of which there are 4 A’s, 2 L’s, and the rest are all different. Therefore, the number of arrangements \(=\frac{9 !}{4 ! 2 !}\)
\(
\begin{aligned}
& =\frac{5 \times 6 \times 7 \times 8 \times 9}{2} \\
& =\frac{15120}{2} \\
& =7560
\end{aligned}
\)

Example 25: How many numbers lying between 100100 and 10001000 can be formed with the digits 1, 2, 3, 4, 5 if the repetition of digits is not allowed?

Solution:

Every number lying between 100 and 1000 is a three-digit number. Therefore, we have to find the number of permutations of five digits \(1,2,3,4,5\) taken three at a time.
Hence, the required number of numbers \(={ }^5 \mathrm{P}_3\)
\(
\begin{aligned}
& =\frac{5}{(5-3) !}=\frac{5 !}{2 !}=5 \times 4 \times 3=60
\end{aligned}
\)

Example 26: In how many ways can we arrange 4 red, 3 yellow, and 2 green balls in a row if the balls of the same colour are congruent?

Solution:

The total number of balls are \(4+3+2=9\).
Out of 9 balls, 4 are red, 3 are yellow, and 2 green.
Therefore, the number of arrangements \(=\frac{9 !}{4 ! 3 ! 2 !}\)
\(
\begin{aligned}
& =\frac{9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{(4 \times 3 \times 2 \times 1)(3 \times 2 \times 1)(2 \times 1)} \\
& =1260
\end{aligned}
\)

Example 27: In how many different ways, the letters of the word ‘PERMUTATIONS′ can be arranged if the vowels are all together?

Solution:

In the word PERMUTATIONS, there are 2 Ts and all the other letters appear only once.
There are 5 vowels in the given word, each appearing only once.
Since they have to always occur together, they are treated as a single object for the time being. This single object together with the remaining 7 objects will account for 8 objects. These 8 objects in which there are 2 Ts can be arranged in \(\frac{8 !}{2 !} \text { ways }\)
Corresponding to each of these arrangements, the 5 different vowels can be arranged in 5 ! ways.
Therefore, the required number of arrangements in this case
\(
=\frac{8 !}{2 !} \times 5 !=2419200
\)

Example 28: In how many of the distinct permutations of the letters in MISSISSIPPI do the four I′s not come together?

Solution:

In the given word MISSISSIPPI, I appears 4 times, S appears 4 times, P appears 2 times, and M appears just once.
Therefore, the number of distinct permutations of the letters in the given word
\(
\begin{aligned}
& =\frac{11 !}{4 ! 4 ! 2 !} \\
& =\frac{11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 !}{4 ! \times 4 \times 3 \times 2 \times 1 \times 2 \times 1} \\
& =\frac{11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5}{4 \times 3 \times 2 \times 1 \times 2 \times 1} \\
& =34650
\end{aligned}
\)
There are 4 I’s in the given word. When they occur together, they are treated as a single object [IIII] for the time being. This single object together with the remaining 7 objects will account for 8 objects.

These 8 objects in which there are 4 S’s and 2 P’s can be arranged in \(\text { 8!/4!2! }\) ways i.e., 840 ways.
Number of arrangements where all I’s occur together \(=840\)
Thus, the number of distinct permutations of the letters in MISSISSIPPI in which four Is do not come together \(=34650-840=33810\)

Example 29: Find the total number of words, with or without meaning, that can be formed with the letters of the word ‘COCONUT’.

Solution:

The word ‘C O C O N U T’ contains 7 letters, and C’s and O’s occur twice.

The number of permutations of \(n\) objects, where \(p_1\) objects are of one kind, \(p_2\) are of the second kind, …, \(p_k\) are of \(k^{\text {th }}\) kind and the rest, if anything left, are of a different kind is given by \(\frac{n !}{p_{1} ! p_{2} ! \ldots \ldots p_{k} !}\)

Hence, the number of words that can be formed by COCONUT \(=\frac{7 !}{2 ! 2 !}\)
\(
\begin{aligned}
& =\frac{7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1 \times 2 \times 1} \\
& =1260
\end{aligned}
\)

Example 30: In how many different ways can the letters of the word THOUGHTS be arranged so that the vowels always come together?

Solution:

Given word: THOUGHTS
Number of letters \(=8\)
T’s \(=2\)
H’s \(=2\)
Number of vowels =2(O, U)
Given that the Vowels should come together. Let us consider 2 vowels as one object.
So, the number of letters for arrangement \(=7\) i.e., (OU)THGHTS
The number of arrangements \(=7 !\)
And two vowels can be arranged in 2 ! ways (also there are 2T’s & 2 H’s)).
Therefore, the total number of ways of arrangements \(=(7 ! \times 2 !) / (2 ! 2 !)\)
\(=7 ! / 2 !\)
\(=(7 \times 6 \times 5 \times 4 \times 3 \times 2 !) / 2 !\)
\(=2520\)

Circular permutation of different things, if clockwise and anticlockwise orders are taken as different.

The number of ways to arrange \(n\) distinct objects along a fixed (In cases where after the numbers have been arranged, the clockwise arrangement and the anti-clockwise arrangement of the numbers are the same) circle is

\(P_n=(n-1) !\)

The number is \((n-1)\) ! instead of the usual factorial \(n\) ! since all cyclic permutations of objects are equivalent because the circle can be rotated. 

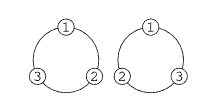
In a linear permutation, i.e., in a row arrangement, there is a start, and there is an end. We need to take into consideration the position of all the people in the arrangement. But in a circular permutation, there is nothing like a start or an end. In a circular permutation, we consider that one person or object is fixed (as shown in the above figure), and the remaining objects are to be arranged. Suppose object \(1\) is fixed, then, the number of ways in which the other two people arrange themselves when one of them has a fixed position is
\(
(3-1) !=2 !=2
\)
There are two possible ways in which three people \(1, 2\) and \(3\) can arrange themselves. The two distinct circular permutations are \(\{1,2,3\} \text { and }\{1,3,2\} \text {. }\) This is also true if we fix the position of \(2\) or \(3\).

Circular permutations of n different things, if clockwise and anticlockwise orders are taken as same

Similarly, for 4 objects (as shown in the figure below) we have \(4 !=24\) permutations of four objects, the \((4-1) !=6\) distinct circular permutations are \(\{1,2,3,4\},\{1,2,4,3\}\), \(\{1,3,2,4\},\{1,3,4,2\},\{1,4,2,3\}\), and \(\{1,4,3,2\}\). Of these, there are only three free permutations (i.e., inequivalent when flipping the circle is allowed): \(\{1,2,3,4\},\{1,2,4,3\}\), and \(\{1,3,2,4\}\). The number of free circular permutations is given by
\(
P_n=\frac{1}{2}(n-1) !
\)
Where \(P_n=\) represents circular permutation and \(n=\) Number of objects.

Example 31: In how many different ways can five people be seated at a circular table?

Solution:

Let us fix the position of one person. Now, we are left with 4 people. The number of arrangements is 4!=4×3×2×1=24 ways.

Example 32: People are invited to a party. In how many ways can they be seated in a circle such that two particular people sit on the sides of the host?

Solution:

Total number of people at the party =31
As two people say A and B are to be seated beside the host, say H, so the number arrangements are AHB and BHA. Now taking [A, H, B] as a single element
Remaining number of guests =29
Hence, the number of arrangements =(29-1)! = 28!
Thus, the number of ways of arrangement besides the host =28!×2

Example 33:Eight people are to be seated in a row of 8 chairs. In how many ways can these people be seated if two of them insist on sitting next to one another?

Solution:

Given there are 8 people and 8 chairs in a row. Since two people insist on sitting next to each other, they are considered as one unit. So now, we have 7 chairs and 7 people. We can arrange them in 7 ! ways.
But we know that the two people(taken as one unit) can interchange their places, i.e. in 2 ways
Therefore, there are \(7 ! \times 2=5040 \times 2=10080\) ways

Example 34: Find the number of ways in which 6 beads can be arranged to form a necklace.

Solution:

Arrangement: to form a necklace (circular permutation)
Let us fix the position of the first bead.
Now, we have left with 5 beads, which can be arranged in 5 ! ways.
As there is no dependency on the position of beads in a clockwise or anticlockwise direction.
Required number of ways \(=\frac{1}{2}(5 !)=60\)

Example 35: Find the number of ways in which 5 people A, B, C, D, and E can be seated at a round table, such that

(i) A and B always sit together.
(ii) C and D never sit together.

Solution:

(i) If we wish to seat A and B together in all arrangements, we can consider these two as one unit, along with 3 others. So, effectively we’ve to arrange 4 people in a circle, the number of ways being (4 – 1)! or 6. Let’s take a look at these arrangements:

But in each of these arrangements, A and B can themselves interchange places in 2 ways. Here’s what I’m talking about:

Therefore, the total number of ways will be 6 x 2 or 12.

(ii) The number of ways, in this case, would be obtained by removing all those cases (from the total possible) in which C and D are together. The total number of ways will be (5 – 1)! or 24. Similar to (i) above, the number of cases in which C and D are seated together, will be 12. Therefore the required number of ways will be 24 – 12 or 12.

The number of circular permutations of m things of the first kind, n things of the second kind, such that no two things of second kind come together

The number of circular permutations of \(m\) things of the first kind, \(n\) things of the second kind, such that no two things of second kind come together is

\((m-1) ! \times^m P_n\)

Example 36: In how many ways can 10 men and 5 women sit around a circular table such that no 2 women sit together?

Solution:

10 men can be seated around a table for 9 ! ways. There are 10 spaces between the men which can be filled up by the 5 women in \({ }^{10} P_5\) ways.
Therefore, total no. of ways of arranging the men and women \(=9 ! \times{ }^{10} P_5\) ways
Total no. of ways of arranging the men and women \(=9 ! \times \frac{10 !}{(10-5) !}\)
\(\therefore\) Total no. of ways of arranging the men and women \(=9 ! \times \frac{10 !}{5 !}\)

The number of circular permutations of m things of first kind, n things of second kind, such that all things of second kind come together

The number of circular permutations of \(m\) things of first kind, \(n\) things of second kind, such that all things of second kind come together is \((m+1-1) ! n !=m ! n !\)

Circular permutations of n different things taken r at a time, when clockwise and anti-clockwise orders are taken as different

The number of circular permutations of \(n\) different things taken \(r\) at a time, when clockwise and anti-clockwise orders are taken as different is
\(\frac{{ }^n P_r}{r}\)

Example 37: In how many ways can 30 people be seated at a round table if there are 8 chairs?

Solution:

As we know, the number of circular permutations of \(n\) different objects taken \(r\) at a time is \(\frac{{ }^n P_r}{r}\), if clockwise and anticlockwise orders are taken as different. For circular permutations, the clockwise and anticlockwise arrangements are different.
Hence, the total number of ways \(=\frac{{ }^{30} P_8}{8}\)

Circular permutations of n different things taken r at a time, when clockwise and anti-clockwise orders are taken as same

As we know, the number of circular permutations of \(n\) different objects taken \(r\) at a time when clockwise and anti-clockwise orders are taken as same is

\(\frac{{ }^n P_r}{2r}\)

Example 38: How many different necklaces can be formed from 20 beads of different colors if 10 beads are required to make a necklace?

Solution:

In the case of the necklace, there is no distinction between the clockwise and anticlockwise arrangements.
So, the required number of circular permutations is \({ }^{20} \mathrm{P}_{10} /(2 \times 10)\)