A linear function is of the form \(f(x)=a x+b\). Since a nonlinear function is a function that is not a linear, its equation can be anything that is not of the form \(f(x)=a x+b\). Some examples of nonlinear functions are:

• \(f(x)=x^2\) is nonlinear as it is a quadratic function.
• \(f(x)=2^x\) is nonlinear as it is an exponential function.
• \(f(x)=x^3-3 x\) is nonlinear as it is a cubic function.

The Zero Product Property

If the product of two or more numbers equals zero, then at least one of the numbers must equal zero. That is, if
\(
a b=0
\)
then
\(
a=0 \text { or } b=0
\)
Let’s use the zero product property to solve a few equations.

Example 1: \(\text { Solve for } x: (x^2-2x-15)=0\)

Solution:

The product of two factors equals zero.
\(
(x+3)(x-5)=0
\)
Hence, at least one of the factors must equal zero. Using the zero product property, set each factor equal to zero, then solve the resulting equations for \(x\).
\(
\begin{aligned}
x+3 & =0 \\
x & =-3
\end{aligned}
\)
or
\(
\begin{aligned}
x-5 & =0 \\
x & =5
\end{aligned}
\)
Hence, the solutions are \(x=-3\) and \(x=5\)
Check:
Check that each solution satisfies the original equation.
Substitute \(-3\) for \(x\) :
\(
\begin{aligned}
(x+3)(x-5) & =0 \\
(-3+3)(-3-5) & =0 \\
(0)(-8) & =0 \\
0 & =0
\end{aligned}
\)
Substitute 5 for \(x\) :
\(
\begin{aligned}
(x+3)(x-5) & =0 \\
(5+3)(5-5) & =0 \\
(8)(0) & =0 \\
0 & =0
\end{aligned}
\)
Because each check produces a true statement, both \(x=-3\) and \(x=5\) are solutions of \((x+3)(x-5)=0\).

Example 2: \(\text { Solve for } x: x(2 x+9)(3 x-5)=0\)

Solution:

The product of three factors equals zero.
\(
x(2 x+9)(3 x-5)=0
\)
Using the zero product property, set each factor equal to zero, then solve the resulting equations for \(x\).
\(
x=0
\)
or
\(
\begin{aligned}
2 x+9 & =0 \\
2 x & =-9 \\
x & =-\frac{9}{2}
\end{aligned}
\)
or
\(
\begin{array}{r}
3 x-5=0 \\
3 x=5 \\
x=\frac{5}{3}
\end{array}
\)
Hence, the solutions are \(x=0, x=-9 / 2\), and \(x=5 / 3\). We encourage the reader to check the solution.

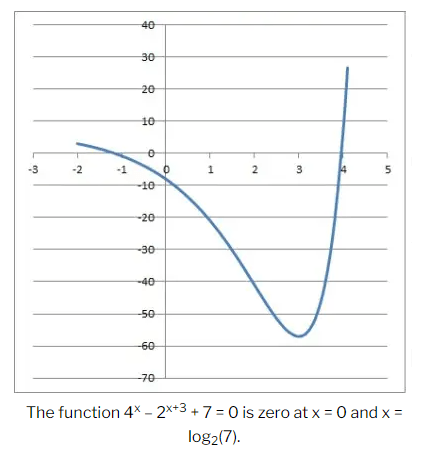
Example 3: Solve for \(x\): \(4^x-2^{x+3}+7=0\)

Solution:

This is a nonlinear equation that includes exponential terms (an exponential equation). The first thing to notice is that we can change the base for the first term, 4 , to match the base of the second term, 2:
\(\left(2^2\right)^x-2^{x+3}+7=0\)
\(2^{2 x}-2^{x+3}+7=0\)
Now we can write the first two terms in terms of \(2^{\mathrm{x}}\) :
\(\left(2^x\right)^2-2^{3} \times 2^x+7=0\)
\(\left(2^x\right)^2-8 \times 2^x+7=0\)
Now, we can substitute \(\mathrm{t}=2^{\mathrm{x}}\) to give us a more familiar equation:
\(t^2-8 t+7=0\)
Now we factor the left side:
\((t-1)(t-7)=0\)
The two solutions of this quadratic equation are \(t=1\) and \(t=7\).
We still need to solve in terms of \(x\).
For \(\mathrm{t}=1\) :
\(2^x=1\)
\(\mathbf{x}=\mathbf{0}\)
For \(\mathrm{t}=7\) :
\(2^x=7\)
\(x=\log _2(7)\)
So, the two solutions to this exponential equation are \(x=0\) and \(x=\log _2(7)\). We can verify this in the graph below:

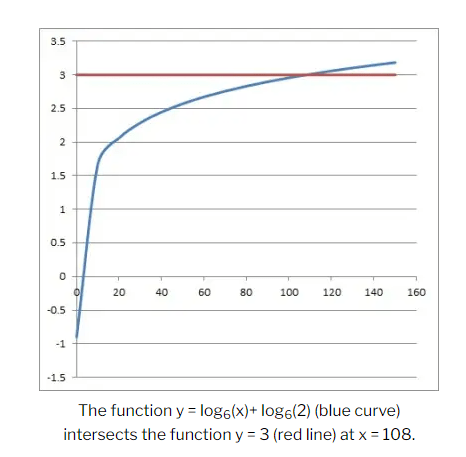
Example 4: Solve for \(x\): \(\log _6(x)+\log _6(2)=3\)

Solution:

This is a nonlinear equation that includes a logarithm (a logarithmic equation). The first thing to notice is that we can use the rules of logarithms to combine the terms on the left side using \(\log _b(X)+\log _b(Y)=\log _b(X Y)\) :
\(\log _6(2 x)=3\)
Now we rewrite the logarithmic equation in exponential form, using the fact that \(\log _b(N)\) \(=\mathrm{E}\) is equivalent to \(\mathrm{b}^{\mathrm{E}}=\mathrm{N}\) :
\(6^3=2 x\)
\(216=2 x\)
\(108=x\)
So, the solution to this logarithmic equation is \(x=108\). We can verify this in the graph below: