Multiplication of a Vector by a Number(Scalar)

Suppose \(\vec{a}\) is a vector of magnitude \(a\) and \(n\) is a number. We define the vector \(\vec{b}=n \vec{a}\) as a vector of magnitude \(|n a|\). If \(n\) is positive the direction of the vector \(\vec{b}=n \vec{a}\) is same as that of \(\vec{a}\).

If \(n\) is negative, the direction of \(\vec{b}\) is opposite to \(\vec{a}\). In particular, multiplication by \((-1\) ) just inverts the direction of the vector. The vectors \(\vec{a}\) and \(-\vec{a}\) have equal magnitudes but opposite directions.

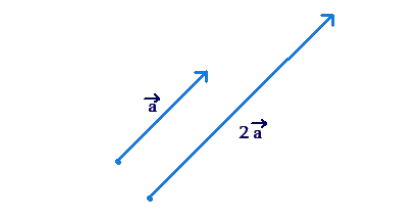
Example-1: Consider a vector \(\vec{a}\). What happens if you multiply this vector by 2? What will the vector \(2 \vec{a}\) represent?

Solution:
Intuitively, the answer should be clear: the new vector will be twice the length of the original vector, but in the same direction:

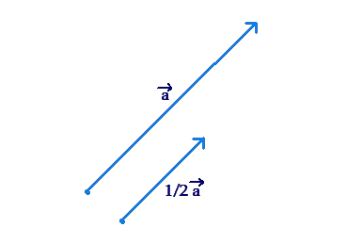
Example-2: \(\text { The vector } \frac{1}{2} \vec{a} \text { will be a vector in the same direction as } \vec{a} \text {, but with a length equal to half of the length of } \vec{a} \text { : }\)

Solution:

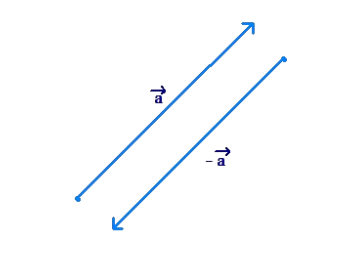
Example-3: \(\text { We have seen how to interpret the vector }-\vec{a} \text {, given the vector } \vec{a} \text { : }\)

Solution: The two vectors are in opposite directions.

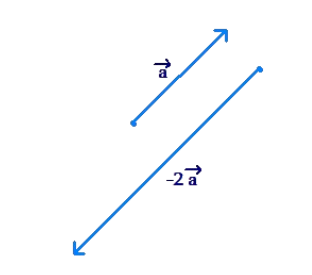
Example-4: What about the vector \(-2 \vec{a}\)? The direction of this vector will be opposite to the direction of \(\vec{a}\), and its length will be twice the length of \(\vec{a}\):

Solution:

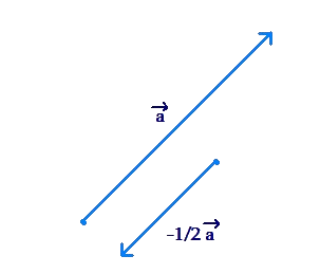
Example 5: The vector \(-\frac{1}{2} \vec{a}\) will have a direction opposite to that of \(\vec{a}\), and will have a length equal to half the length of \(\vec{a}\):

Solution: