Maxima/Minima by Using Derivatives

The concept of slope, and hence the derivatives, is used to find the maximum or minimum value of a function. There are two tests that use derivatives and are used to find the maxima/minima of a function. They are

• First Derivative test
• Second derivative test

First Derivative Test

We can just use the first derivative to determine the maximum or minimum by observing the following points:

• \(f^{\prime}(x)\) represents the slope of a tangent line.
• If \(f^{\prime}(x)\) changes sign from positive to negative as \(x\) increases through point \(c\), then \(c\) is the point of local maxima. And the \(f(c)\) is the maximum value.
• If \(f^{\prime}(x)\) changes sign from negative to positive as \(x\) increases through point \(c\), then \(c\) is the point of local minima. And the \(f(c)\) is the minimum value.
• If \(f^{\prime}(x)\) doesn’t change sign as \(x\) increases through \(c\), then \(c\) is neither a point of local nor a point of local maxima. It will be called the point of inflection.
• Note that \(f^{\prime}(x)=0\) at local maximum and local minimum.

Second Derivative Test

The second derivative test uses the critical points and the second derivative to find the maxima/minima. To perform this test:

• \(x=c\) will be point of local maxima if \(f^{\prime}(c)=0\) and \(f^{\prime \prime}(c)<0\). Then \(f(c)\) will be having local maximum value.
• \(x=c\) will be point of local minima if \(f^{\prime}(c)=0\) and \(f f^{\prime \prime}(c)>0\). Then \(f(c)\) will be having local minimum value.
• When both \(f^{\prime}(c)=0\) and \(f^{\prime \prime}(c)=0\) the test fails. And that first derivative test will give you the value of local maxima and minima.
• If \(f^{\prime \prime}(x)=0\), the function neither has maxima nor minima at that point and in this case, it is known as the point of inflection.

Properties of maxima and minima

• If \(\mathrm{f}(\mathrm{x})\) is a continuous function in its domain, then at least one maximum or one minimum should lie between equal values of \(f(x)\).
• Maxima and minima occur alternately. i.e between two minima there is one maxima and vice versa.
• If \(f(x)\) tends to infinity as \(x\) tends to \(a\) or \(b\) and \(f^{\prime}(x)=0\) only for one value \(x\) i.e.c between a and \(b\), then \(f(c)\) is the minimum and the least value. If \(f(x)\) tends to \(-\infty\) as \(x\) tends to \(a\) or \(b\), then \(f(c)\) is the maximum and the highest value.

Example 38: Find the maxima and minima for \(y=5 x^3+2 x^2-3 x\)

Solution:

The derivative (slope) is:
\(
\frac{d}{d x} y=15 x^2+4 x-3
\)
Which is quadratic with zeros at:
\(x=-3 / 5\)
\(x=+1 / 3\)
Could they be maxima or minima? (Don’t look at the graph yet!)
The second derivative is \({y}^{\prime \prime}={3 0 x}+{4}\)
At \(x=-3 / 5\) :
\(
y^{\prime \prime}=30(-3 / 5)+4=-14
\)
it is less than 0 , so \(-3 / 5\) is a local maximum
At \(x=+1 / 3\)
\(
y^{\prime \prime}=30(+1 / 3)+4=+14
\)
it is greater than 0 , so \(+1 / 3\) is a local minimum

Let’s look at the graph below.

 

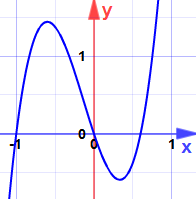
Example 39: Find the local maxima and local minima of the function \(f(x)=2 x^3+3 x^2-12 x+5\), using the first derivative test.

Solution:

The given function is \(f(x)=2 x^3+3 x^2-12 x+5\)
\(
f^{\prime}(x)=6 x^2+6 x-12
\)
\(
f^{\prime}(x)=0 ; 6 x^2-6 x-12=0,6\left(x^2+x-2\right)=0,6(x-1)(x+2)=0
\)
Hence the limiting points are \(x=1\), and \(x=-2\).
Let us take the points in the immediate neighborhood of \(x=1\).
The points are \(\{0,2\}\).
\(f^{\prime}(0)=6\left(0^2+0-2\right)=6(-2)=-12\), and \(f^{\prime}(2)=6\left(2^2+2-2\right)=6(4)=\) \(+24\)

The derivative of the function is negative towards the left of \(x=1\), and is positive towards the right. Hence \(x=1\) is the local minima.
Let us now take the points in the immediate neighborhood of \(x=\) -2. The points are \(\{-3,-1\}\).
\(f^{\prime}(-3)=6\left((-3)^2+(-3)-2\right)=6(4)=+24\), and \(f^{\prime}(-1)=6\left((-1)^2+(-1)\right.\) \(-2)=6(-2)=-12\)

The derivative of the function is positive towards the left of \(x=\) \(-2\) and is negative towards the right. Hence \(x=-2\) is the local maxima.

Therefore, the local maxima is \(-2\), and the local minima is \(-1\).

Example 40: Find the local maxima and local minima of the function \(f(x)=x^3-6 x^2+9 x+15\), using second derivative test.

Solution:

The given function is \(f(x)=x^3-6 x^2+9 x+15\). \(f^{\prime}(x)=3 x^2-12 x+9\). Let us find the zeros of the expression. \(f^{\prime}(x)=\) 0 .
\(
f^{\prime}(x)=3\left(x^2-4 x+3\right)
\)
\(x^2-4 x+3=0\) or \((x-1)(x-3)=0\)
Here \(x=1\), and \(x=3\)
\(
f^{\prime \prime}(x)=6 x-12
\)
\(f^{\prime \prime}(1)=6(1)-12=6-12=-6 ., f^{\prime \prime}(1)<0\), and \(x=1\) is the maxima. \(f^{\prime \prime}(3)=6(3)-12=18-12=6, f^{\prime \prime}(3)>0\), and \(x=3\) is the minima.
Therefore by using the second derivative test, the local maxima is 1, with a maximum value of \(f(1)=19\), and the local minima is 3, with a minimum value of \(f(3)=15\)

Example 41: \(\text { Find the local maxima and minima of the function } f(x)=3 x^4+4 x^3-12 x^2+12\)

Solution:

For stationary points \(f^{\prime}(x)=0\).
\(
\begin{aligned}
&f^{\prime}(x)=12 x^3+12 x^2-24 x=0 \\
&\Rightarrow 12 x\left(x^2+x-2\right)=0 \\
&\Rightarrow 12 x(x-1)(x+2)=0 \\
&=>\text { Hence, } x=0, x=1 \text { and } x=-2
\end{aligned}
\)
Second derivative test:
\(
\begin{aligned}
&f^{\prime \prime}(x)=36 x^2+24 x-24 \\
&f^{\prime \prime}(x)=12\left(3 x^2+2 x-2\right)
\end{aligned}
\)
At \(x=-2\)
\(
f^{\prime \prime}(-2)=12\left(3(-2)^2+2(-2)-2\right)=12(12-4-2)=12(6)=72>0
\)
At \(x=0\)
\(
f^{\prime \prime}(0)=12\left(3(0)^2+2(0)-2\right)=12(-2)=-24<0
\)
At \(x=1\)
\(
f^{\prime \prime}(1)=12\left(3(1)^2+2(1)-2\right)=12(3+2-2)=12(3)=36>0
\)
Therefore, by the second derivative test \(x=0\) is the point of local maxima while \(x=-2\) and \(x=1\) are the points of local minima.

Example 42: \(\text { Find the maxima and minima for } f(x)=2 x^3-21 x^2+36 x-15\)

Solution:

We have \(f(x)=2 x^3-21 x^2+36 x-15\)
\(
f^{\prime}(x)=6 x^2-42 x+36
\)
Now find the points where \(f^{\prime}(x)=0\)
\(
\begin{aligned}
&f^{\prime}(x)=0 \Rightarrow 6 x^2-42 x+36=0 \\
&\Rightarrow x^2-7 x+6=0 \\
&\Rightarrow(x-6)(x-1)=0
\end{aligned}
\)
\(\Rightarrow x=6\) or \(x=1\) are the possible points of minima or maxima.
Let us test the function at each of these points.
\(
f^{\prime \prime}(x)=12 x-42
\)
At \(x=1, f^{\prime \prime}(1)=12-42=-30<0\)
Therefore \(x=1\) is a point of local maximum.
The maximum value is \(f(1)=2-21+36-15=2\)
At \(x=6, f^{\prime \prime}(x)=12 \times 6-42=30>0\)
Therefore \(x=6\) is a point of local minimum.
The local minimum value is \(f(6)=2(6)^3-21(6)^2+36(6)-15\)
\(=2 \times 216-21 \times 36+216-15\)
\(
=432-756+216-15=-123
\)

Convergence/Divergence of Series

If the sequence of partial sums is a convergent sequence (i.e. its limit exists and is finite) then the series is also called convergent and in this case if \(\lim _{n \rightarrow \infty} s_n=s\) then, \(\sum_{i=1}^{\infty} a_i=s\). If the sequence of partial sums is a divergent sequence (i.e. its limit doesn’t exist or is plus or minus infinity) then the series is also called divergent. 

Example 43: Determine if the following series is convergent or divergent. If it converges determine its value.
\(
\sum_{n=1}^{\infty} n
\)

Solution: To determine if the series is convergent we first need to get our hands on a formula for the general term in the sequence of partial sums.
\(
s_n=\sum_{i=1}^n i
\)
This is a known series and its value can be shown to be,
\(
s_n=\sum_{i=1}^n i=\frac{n(n+1)}{2}
\)
Don’t worry if you didn’t know this formula (we’d be surprised if anyone knew it…) as you won’t be required to know it in my course.
So, to determine if the series is convergent we will first need to see if the sequence of partial sums,
\(
\left\{\frac{n(n+1)}{2}\right\}_{n=1}^{\infty}
\)
is convergent or divergent. That’s not terribly difficult in this case. The limit of the sequence terms is,
\(
\lim _{n \rightarrow \infty} \frac{n(n+1)}{2}=\infty
\)
Therefore, the sequence of partial sums diverges to \(\infty\) and so the series also diverges.

Example 44: Determine if the following series converges or diverges. If it converges determine its sum.
\(
\sum_{n=2}^{\infty} \frac{1}{n^2-1}
\)

Solution: This is actually one of the few series in which we are able to determine a formula for the general term in the sequence of partial fractions. However, in this section we are more interested in the general idea of convergence and divergence and so we’ll put off discussing the process for finding the formula until the next section.
The general formula for the partial sums is,
\(
s_n=\sum_{i=2}^n \frac{1}{i^2-1}=\frac{3}{4}-\frac{1}{2 n}-\frac{1}{2(n+1)}
\)
and in this case we have,
\(
\lim _{n \rightarrow \infty} s_n=\lim _{n \rightarrow \infty}\left(\frac{3}{4}-\frac{1}{2 n}-\frac{1}{2(n+1)}\right)=\frac{3}{4}
\)
The sequence of partial sums converges and so the series converges also and its value is,
\(
\sum_{n=2}^{\infty} \frac{1}{n^2-1}=\frac{3}{4}
\)

Relations and Functions

What Is a Relation?

A relation is any set of ordered pairs. An ordered-pair is a pair of values that go together. For example, \((4,7)\) is an ordered-pair number; the order is designated by the first element 4 and the second element 7 . In other words a relation shows a relationship between two values or we can define a relation as a bunch of ordered pairs.

What Is A Function?

In mathematics, a function can be defined as a rule that relates every element in one set, called the domain, to exactly one element in another set, called the range. For example, \(y=x+3\) and \(y=x^2-1\) are functions because every \(x\)-value produces a different \(y\)-value.

A function is a relation in which each element in the domain matches exactly one element in the range. Alternatively, a function is a relation where each input has only one output.

• A function is a relation in which each x-element has only one \(y\) element associated with it. Given a set of ordered pairs, a relation is a function if there are no repeated \(x\)-value.
• A relation is a function if there are no vertical lines that intersect its graph at more than one point. This is called the vertical line test.

Function & Relation Difference

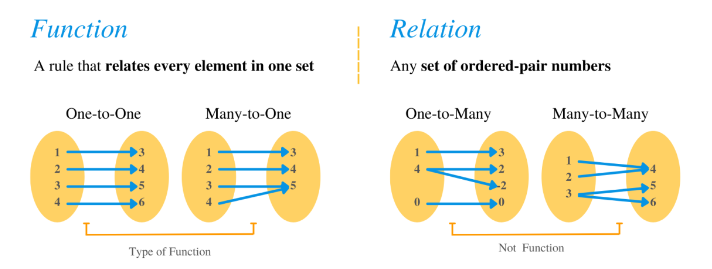
Note: All functions are relations, but not all relations are functions.

Table of Values

One way to represent the relationship between the input and output variables in a relation or function is by means of a table of values.
\(
\begin{array}{|c|c|}
\hline x & y \\
\hline 2 & -1 \\
\hline 1 & -2 \\
\hline 1 & 3 \\
\hline 0 & 2 \\
\hline
\end{array}
\)

What is a Set?

A set is a collection of distinct or well-defined members or elements. In mathematics, members of a set are written within curly braces or brackets { }. Members of assets can be anything such as; numbers, people, or alphabetical letters, etc.

For example, \(\{a, b, c, \ldots, x, y, z\}\) is a set of alphabet letters.

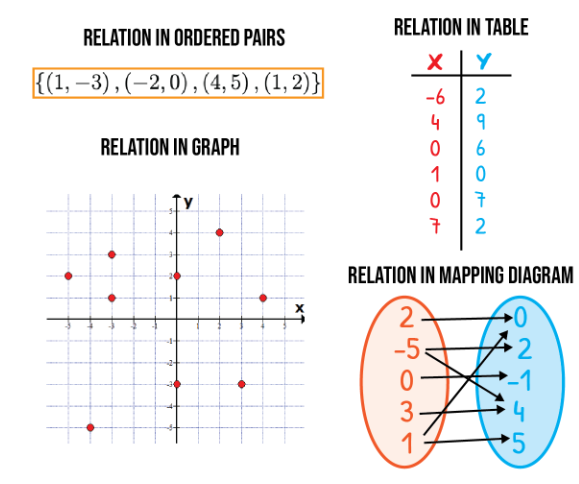
Ordered Pairs

Relations and functions can also be represented as a set of points or ordered pairs. These are numbers that go hand in hand. Ordered pair numbers are represented within parentheses and separated by a comma. For example, (6,8) (input, output) is an ordered-pair number whereby the numbers 6 and 8 are the first (input) and second (output) elements, respectively.
\(
\{(1,-3),(-2,0),(4,5),(1,2)\}
\)

Ways to Represent Relation

What is Domain and Range?

The domain and range of a relation are the sets of all the \(x\) -coordinates and all the \(y\)-coordinates of ordered pairs respectively. For example, if the relation is, \(R=\{(1,2),(2,2),(3,3),(4,3)\}\), then:

• Domain \(=\) the set of all \(x\)-coordinates \(=\{1,2,3,4\}\)
• Range \(=\) the set of all \(y\)-coordinates \(=\{2,3\}\)

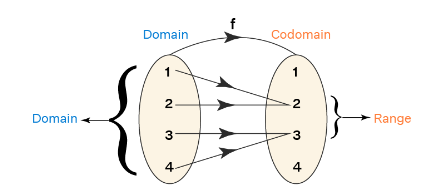
Domain and Range of a Function

The domain and range of a function are the components of a function. The domain is the set of all the input values of a function and the range is the possible output given by the function. Domain \(\rightarrow\) Function \(\rightarrow\) Range. If there exists a function \(f: A \rightarrow B\) such that every element of \(\operatorname{set} A\) is mapped to elements in set \(B\), then \(A\) is the domain and \(B\) is the codomain. The image of an element ‘a’ under a relation \(R\) is given by ‘ \(b\) ‘, where \((a, b) \in R\). The range of the function is the set of images. The domain and range of a function are denoted in general as follows: Domain \((f)=\{x \in R\) : Condition \(\}\) and range \((f)=\{f(x): x \in\) domain \((f)\}\)

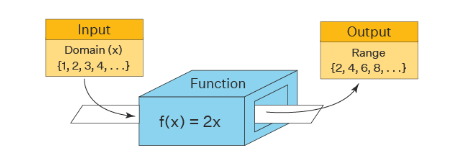
The domain and range of this function \(f(x)=2 x\) is given as domain \(D=\{x\) \(\in N\}\), range \(R=\{y \in N: y=2 x\}\)

Domain of a Function

The domain in math is the set of all possible inputs for the function. Consider the above box as a function \(f(x)=2 x\). Inputting the values \(x=\{1,2,3,4, \ldots\}\), the domain is simply the set of natural numbers. But in general (if the domain is not specified as natural numbers), \(f(x)=2 x\) is defined for all real values of \(x\) and hence its domain is the set of all real numbers which is denoted by (\(\infty, \infty)\). Here are the general formulas used to find the domain of different types of functions. Here, R is the set of all real numbers.

How to Find the Domain of a function

• To find the domain, we need to look at the values of the independent variables which are allowed i.e. no zero at the bottom of the fraction and no negative sign inside the square root.
• Domain of a square root function \(\sqrt{x}\) is \(x \geq 0\).
• To find the domain of a rational function \(y=f(x)\), set the denominator \(\neq 0\).
• Domain of any polynomial (linear, quadratic, cubic, etc. ) function is \(R\) (all real numbers).
• In general, the set of all real numbers \(( R )\) is considered as the domain of a function subject to some restrictions. They are:
  • When the given function is of the form \(f(x)=2 x+5\) or \(f(x)=x^2-2\), the domain will be “the set of all real numbers.
  • When the given function is of the form \(f(x)=1 /(x-1)\), the domain will be the set of all real numbers except 1.
• In some cases, the interval be specified along with the function such as \(f(x)=3 x+4,2<x\) < 12. Here, \(x\) can take the values between 2 and 12 as input (i.e. domain).
• Domain of an exponential function is \(R\).
• Domain of logarithmic function is \(x>0\).
• Domain restrictions refer to the values for which the given function cannot be defined.

Example 45: Find the domain of a function \(f(x)=\sqrt{ }(x+2)\)

Solution: we apply the rule  mentioned above (\(\sqrt{x}\) is \(x \geq 0\)). Then we get: \(x+2 \geq 0\). Solving this inequality, we get \(x \geq-2\). Thus, the domain of \(f(x)\) is \([-2, \infty)\).

Example 46: calculate the domain of a function \(g(x)=(2 x+1) /(x-2)\)

Solution: we apply the rule mentioned above. Then we get \(x-2 \neq 0\). Solving this, we get \(x \neq 2\). Thus, its domain is the set of all real numbers except 2 which in interval notation can be written as \((-\infty, 2) \cup(2, \infty)\).

Range of a Function

The range of a function is the set of all its outputs. Example: Let us consider the function \(f: A \rightarrow B\), where \(f(x)=2 x\) and each of \(A\) and \(B=\{\) set of natural numbers}. Here we say \(A\) is the domain and \(B\) is the co-domain. Then the output of this function becomes the range. The range \(=\) {set of even natural numbers}. The elements of the domain are called preimages and the elements of the co-domain which are mapped are called the images. Here, the range of the function \(f\) is the set of all images of the elements of the domain (or) the set of all the outputs of the function.

How to Find the Range of a Function

Consider a function \(y=f(x)\).

• The spread of all the \(y\) values from minimum to maximum is the range of the function.
• In the given expression of y , substitute all the values of x to check whether it is positive, negative or equal to other values.
• Find the minimum and maximum values for \(y\).
• Range of a linear function is \(R\).
• Range of a quadratic function \(y=a(x-h)^2+k\) is: \(y \geq k\), if \(a>0\) and \(y \leq k\), if \(a<0\)
• Range of a square root function is \(y \geq 0\).
• Range of an exponential function is \(y>0\).
• Range of logarithmic function is \(R\).
• To find the range of a rational function \(y=f(x)\), solve it for \(x\) and set the denominator \(\neq 0\).
• Then draw a graph for the same.

Example 47: Calculate the range of the function \(f(x)=2(x-3)^2-5\),

Solution: Apply rule (Range of a quadratic function) mentioned above. Then its range is \(y \geq-5\) (or) \([-5, \infty)\).

Example 48: Find the range of a function \(g(x)=\ln (2 x-3)+4\)

Solution: We apply the rule above (Range of logarithmic function is \(R\).) . Then we get its range to be the set of all real numbers \(( R )\).

Codomain

In relations and functions, the codomain is the set of all possible outcomes of the given relation or function. Sometimes, the codomain is also equal to the range of the function. However, the range is the subset of the codomain.

As we said, the codomain of a real function is considered as the set of real numbers, unless explicitly stated otherwise. Thus, algebraic functions (polynomial, constant, linear, quadratic, rational, irrational, etc.) and transcendental functions (exponential, logarithmic, trigonometric, and hyperbolic) have the set of real numbers as their codomain. The following table shows examples of real functions and their domains, codomains, and ranges.

\(
\begin{array}{cccc}
\text { Function } & \text { Domain } & \text { Codomain } & \text { Range } \\
y=2 x+1 & R & R & R \\
y=3 & R & R & \{3\} \\
y=x^2 & R & R & {[0,+\infty)} \\
y=1 / x & R -\{0\} & R & R -\{0\} \\
y=\sqrt{x-1} & {[1,+\infty)} & R & {[0,+\infty)} \\
y=e^x & R & R & (0,+\infty) \\
y=\ln (x) & (0,+\infty) & R & R \\
y=\cos (x) & R & R & {[-1,1]}
\end{array}
\)

Domain and Range of Trigonometric Functions

Look at the graph of the sine function and cosine function. Notice that the value of the functions oscillates between -1 and 1 and it is defined for all real numbers. Thus, for each of the sine and cosine functions:

• Domain: The domain of the functions is the set \(R\) (or) \((-\infty,+\infty)\).
• Range: The range of the functions is \([-1,1]\)

\(
\begin{array}{|l|l|l|}
\hline \begin{array}{l}
\text { Trigonometric } \\
\text { Functions }
\end{array} & \text { Domain } & \text { Range } \\
\hline \sin \theta & (-\infty,+\infty) & {[-1,+1]} \\
\hline \cos \theta & (-\infty+\infty) & {[-1,+1]} \\
\hline \tan \theta & R -(2 n+1) \pi / 2 & (-\infty,+\infty) \\
\hline \cot \theta & R -n \pi & (-\infty,+\infty) \\
\hline \sec \theta & R -(2 n+1) \pi / 2 & (-\infty,-1] \cup[+1,+\infty) \\
\hline \operatorname{cosec} \theta & R -n \pi & (-\infty,-1] \cup[+1,+\infty) \\
\hline
\end{array}
\)

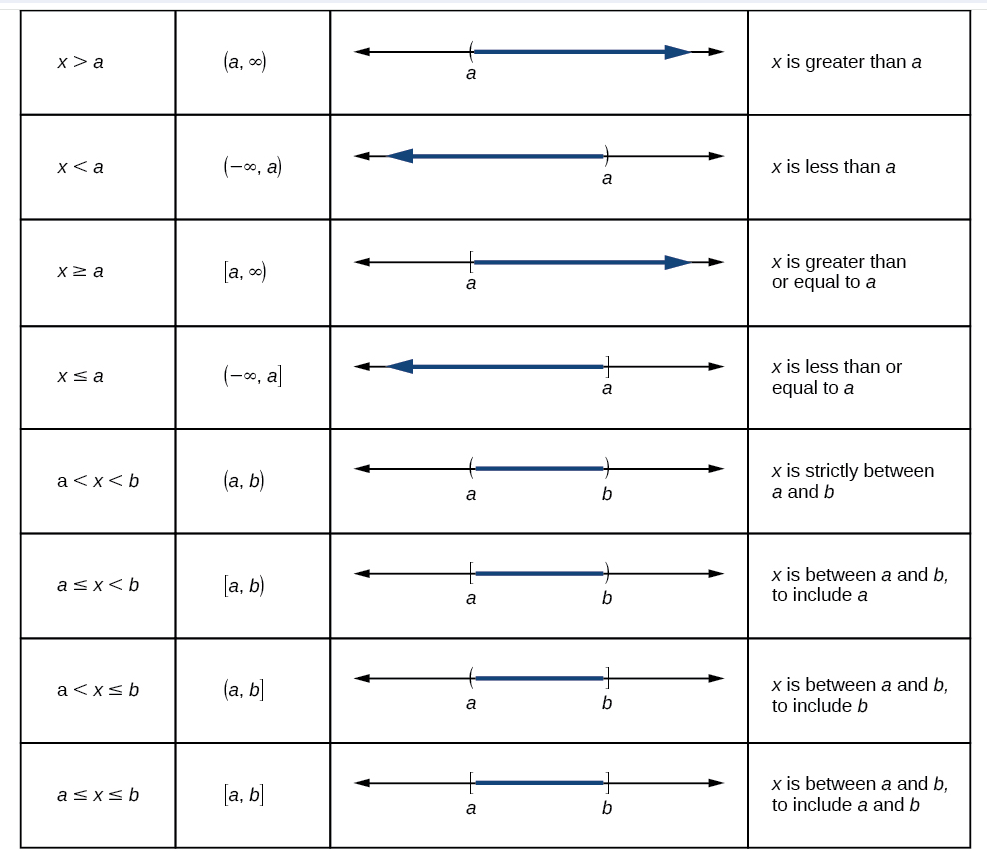
Review the conventions of interval notation:

• The smallest term from the interval is written first.
• The largest term in the interval is written second, following a comma.
• Parentheses, ( or ), are used to signify that an endpoint is not included, called exclusive.
• Brackets, [ or ], are used to indicate that an endpoint is included, called inclusive.

Summary:

• The domain is defined as the entire set of values possible for independent variables.
• The Range is found after substituting the possible \(x\) – values to find the \(y\)-values.

Example 48: Determine whether the following are functions
(a) \(A=\{(1,2),(2,3),(3,4),(4,5)\}\)
(b) \(B=\{(1,3),(0,3),(2,1),(4,2)\}\)
(c) \(C=\{(1,6),(2,5),(1,9),(4,3)\}\)

Solution: (a) \(A=\{(1,2),(2,3),(3,4),(4,5)\}\) is a function because all the first elements are different.
(b) \(B=\{(1,3),(0,3),(2,1),(4,2)\}\) is a function because all the first elements are different. (The second element does not need to be unique)
(c) \(C=\{(1,6),(2,5),(1,9),(4,3)\}\) is not a function because the first element, 1 , is repeated.