Maxima and Minima

Suppose a quantity \(y\) depends on another quantity \(x\) in a manner shown in figure (below). It becomes maximum at \(x_1\) and minimum at \(x_2\).

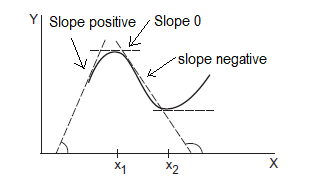
At these points the tangent to the curve is parallel to the \(X\)-axis and hence its slope is \(\tan \theta=0\). But the slope of the curve \(y-x\) equals the rate of change \(\frac{d y}{d x}\). Thus, at a maximum or a minimum,
\(
\frac{d y}{d x}=0 .
\)

Just before the maximum, the slope is positive, at the maximum, it is zero and just after the maximum, it is negative. Thus, \(\frac{d y}{d x}\) decreases at a maximum, and hence the rate of change of \(\frac{d y}{d x}\) is negative at a maximum i.e.

\(
\frac{d}{d x}\left(\frac{d y}{d x}\right)<0 \text { at a maximum. }
\)

The quantity \(\frac{d}{d x}\left(\frac{d y}{d x}\right)\) is the rate of change of the slope. It is written as \(\frac{d^2 y}{d x^2}\). Thus, the condition of a maximum is

\(
\left.\begin{array}{l}
\frac{d y}{d x}=0 \\
\frac{d^2 y}{d x^2}<0
\end{array}\right) \text { – maximum. } \dots(1)
\)

Similarly, at a minimum, the slope changes from negative to positive. The slope increases at such a point and hence \(\frac{d}{d x}\left(\frac{d y}{d x}\right)>0\). The condition of a minimum is

\(
\left.\begin{array}{l}
\frac{d y}{d x}=0 \\
\frac{d^2 y}{d x^2}>0
\end{array}\right) \text { – minimum. } \dots(2)
\)

Quite often it is known from the physical situation whether the quantity is a maximum or a minimum. The test on \(\frac{d^2 y}{d x^2}\) may then be omitted.

Example 1: Find the points of maxima and minima of a function:y \(=2 x^3-3 x^2+6\)

Solution: 

Given function: \(y=2 x^3-3 x^2+6\)
Using second-order derivative test for the maxima and minima of a function:
Taking first order derivative of:
\(
y=2 x^3-3 x^2+6 \cdots(\text { eq } 1)
\)
Differentiate both sides (eq 1), w.r.t x.
\(
\begin{aligned}
&\Rightarrow d y / d x=d\left(2 x^3\right) / d x-d\left(3 x^2\right) / d x+d(6) / d x \\
&\Rightarrow d y / d x=6 x^2-6 x+0 \\
&\Rightarrow d y / d x=6 x^2-6 x \cdots(e q \text { 2) }
\end{aligned}
\)
Putting \(\mathrm{dy} / \mathrm{dx}=0\) to find critical points,
\(
\begin{aligned}
&\Rightarrow 6 x^2-6 x=0 \\
&\Rightarrow 6 x(x-1)=0 \\
&\Rightarrow x=0,1
\end{aligned}
\)
The critical points are \(0 \& 1\).
Differentiate both sides of (eq 2), w.r.t x.
\(
\begin{aligned}
&\Rightarrow d^2 y / d x^2=d\left(6 x^2\right) / d x-d(6 x) / d x \\
&\Rightarrow d^2 y / d x^2=12 x-6
\end{aligned}
\)
The critical points are \(0 \& 1\).
Differentiate both sides of (eq 2), w.r.t \(x\).
\(
\begin{aligned}
&\Rightarrow d^2 y / d x^2=d\left(6 x^2\right) / d x-d(6 x) / d x \\
&\Rightarrow d^2 y / d x^2=12 x-6
\end{aligned}
\)
Now, put the values of \(x\) and find the max or min value.
At \(x=0, d^2 y / d x^2=12(0)-6=-6<0\), hence \(x=0\) is a point of maxima
At \(x=1, d^2 y / d x^2=12(1)-6=6>0\), hence \(x=1\) is a point of minima

Example 2: Example: A ball is thrown in the air. Its height at any time \(t\) is given by:
\(h=3+14 t-5 t^2\)
What is its maximum height?

Solution:

Using derivatives we can find the slope of that function:
\(
\begin{aligned}
\frac{d}{d t} h &=0+14-5(2 t) \\
&=14-10 t
\end{aligned}
\)
Now find when the slope is zero:
\(
\begin{aligned}
&14-10 t=0 \\
&10 t=14 \\
&t=14 / 10=1.4
\end{aligned}
\)
The slope is zero at \(\mathbf{t}=\mathbf{1 . 4}\) seconds
And the height at that time is:
\(
\begin{aligned}
&h=3+14 \times 1.4-5 \times 1.4^2 \\
&h=3+19.6-9.8=12.8
\end{aligned}
\)
So, The maximum height is \(12.8 \mathrm{~m}\) (at \(t=1.4 \mathrm{~s})\)

Example 3: The height reached in time t by a particle thrown upward with a speed \(u\) is given by
\(h=u t-\frac{1}{2} g t^2\)
where \(g=9 \cdot 8 \mathrm{~m} / \mathrm{s}^2\) is a constant. Find the time taken in reaching the maximum height.

Solution:

The height \(h\) is a function of time. Thus, \(h\) will be maximum when \(\frac{d h}{d t}=0\). We have,
\(
\begin{aligned}
h &=u t-\frac{1}{2} g t^2 \\
\text { or, } \quad \quad \frac{d h}{d t} &=\frac{d}{d t}(u t)-\frac{d}{d t}\left(\frac{1}{2} g t^2\right)
\end{aligned}
\)
\(
\begin{aligned}
&=u \frac{d t}{d t}-\frac{1}{2} g \frac{d}{d t}\left(t^2\right) \\
&=u-\frac{1}{2} g(2 t)=u-g t .
\end{aligned}
\)
For maximum \(h\),
\(
\frac{d h}{d t}=0
\)
or, \(\quad u-g t=0 \quad\) or, \(\quad t=\frac{u}{g}\).