Definition Of Limits

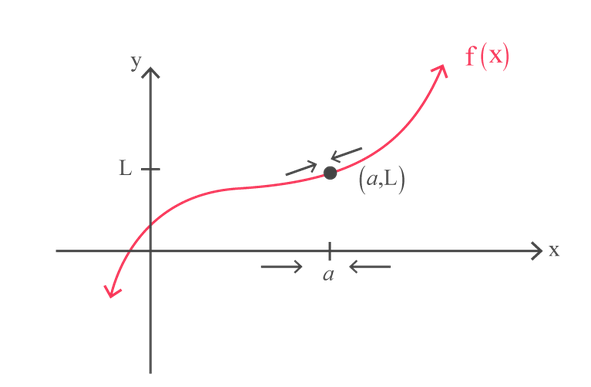
We express limit of a function \(f(x)\) as
\(\lim _{x \rightarrow a} f(a)=L\)
and say “the limit of \(f(x)\), as \({x}\) approaches a, equals \({L}\)
if we can make the values of \(f(x)\) arbitrarily close to \(L\) by taking \(x\) to be sufficiently close to “a” (on either side of \(\mathrm{a}\) ) but not equal to “a”.

This says that as \(x\) gets closer and closer to the number “a” (from either side of a) the values of \(f(x)\) get closer and closer to the number \(L\). In finding the limit of \(f(x)\) as \(x\) approaches. The only thing that matters is how \(f{x})\) is defined near \(a\).

What is the Limit Theorem?

As \(x\) approaches \(a\), the limit of \(f(x)\) is \(L\), if the limit from the left exists and the limit from the right exists and both limits are \(L\).

\(\lim _{x \rightarrow a} f(a)=L\)

How to Find Limit on a Graphy

All this definition says is that, as we approach a specific (finite) value along the \(x\)-axis from both the left and the right sides, we want to find what the \(y\)-value \((L)\) is approaching.

One & Two Sided Limits

Sometimes we are just interested in what’s happening as we approach from only one side, either from the right or from the left. This is known as a one-sided limit. 

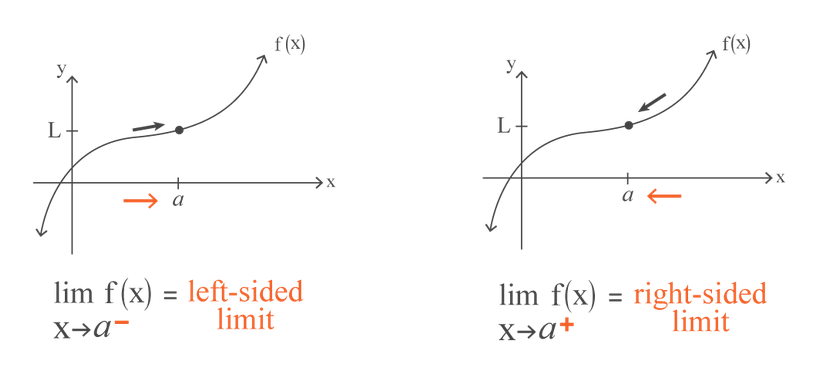
But our formal definition of a limit is called a two-sided limit, as it asks us to approach from both the left and the right. But what happens if we can’t determine what the y-value is approaching?

If f(x) doesn’t approach a specific finite value as x approaches “a” from both directions, then we say that the limit does not exist.

Limit Evaluation using Direct Substitution Property

Example 1: Evaluate the following Limits \(\lim _{x \rightarrow 5}\left(2 x^2-3 x+4\right)\)

Solution: \(\lim _{x \rightarrow 5}\left(2 x^2-3 x+4\right)=2\left(5^2\right)-3(5)+4=39\)

Example 2: \(\lim _{x \rightarrow-2} \frac{x^3+2 x^2-1}{5-3 x}\)

Solution: \(\lim _{x \rightarrow-2} \frac{x^3+2 x^2-1}{5-3 x}=\frac{(-2)^3+2(-2)^2-1}{5-3(-2)}=-\frac{1}{11}\)

Limit Evaluation using Factoring And Canceling

Example 3: Find \(\lim _{x \rightarrow 1} \frac{x^2-1}{x-1}\)

Solution:

We can’t find the limit by substituting \(x=1\) because
\(\frac{(1)^2-1}{1-1}=\frac{0}{0}\) is undefined.
Instead, we need to do some preliminary algebra. We factor the numerator as a difference of squares and then cancel out the common term \((x-1)\)
Therefore,
\(
\begin{aligned}
\lim _{x \rightarrow 1} \frac{x^2-1}{x-1} &=\lim _{x \rightarrow 1} \frac{(x-1)(x+1)}{(x-1)} \\
&=\lim _{x \rightarrow 1}(x+1) \\
&=1+1=2
\end{aligned}
\)

If there are fractions within fractions, try to combine the fractions

Example 4: \(\text { Find } \lim _{x \rightarrow-4} \frac{\frac{1}{4}+\frac{1}{x}}{4+x}\)

Solution:

We cannot use the substitution method because the numerator and denominator would be zero.
\(
\begin{aligned}
\lim _{x \rightarrow-4} \frac{\frac{1}{4}+\frac{1}{x}}{4+x} &=\lim _{x \rightarrow-4} \frac{\frac{x}{4 x}+\frac{4}{4 x}}{4+x} \\
&=\lim _{x \rightarrow-4} \frac{\frac{x+4}{4 x}}{4+x} \\
&=\lim _{x \rightarrow-4} \frac{x+4}{4 x} \cdot \frac{1}{x+4} \\
&=\lim _{x \rightarrow-4} \frac{1}{4 x}=\frac{1}{4(-4)}=-\frac{1}{16}
\end{aligned}
\)

If there is a square root, try to multiply by the conjugate

Example 5: \(\text { Find } \lim _{x \rightarrow 0} \frac{\sqrt{x^2+9}-3}{x^2}\)

Solution:

We cannot use the substitution method because the numerator and denominator would be zero.
\(
\begin{aligned}
\lim _{x \rightarrow 0} \frac{\sqrt{x^2+9}-3}{x^2} &=\lim _{x \rightarrow 0} \frac{\sqrt{x^2+9}-3}{x^2} \cdot \frac{\sqrt{x^2+9}+3}{\sqrt{x^2+9}+3} \\
&=\lim _{x \rightarrow 0} \frac{\left(\sqrt{x^2+9}\right)^2-3^2}{x^2\left(\sqrt{x^2+9}+3\right)} \\
&=\lim _{x \rightarrow 0} \frac{x^2+9-9}{x^2\left(\sqrt{x^2+9}+3\right)} \\
&=\lim _{x \rightarrow 0} \frac{x^2}{x^2\left(\sqrt{x^2+9}+3\right)} \\
&=\lim _{x \rightarrow 0} \frac{1}{\left(\sqrt{x^2+9}+3\right)} \\
&=\frac{1}{\sqrt{9}+3}=\frac{1}{3+3}=\frac{1}{6}
\end{aligned}
\)

Limits Formula

The following are the important limits formulas:

Limits of Exponential and Log Functions

\(
\lim _{x \rightarrow 0} e^x=1
\)
\(\lim _{x \rightarrow 0} \frac{e^x-1}{x}=1\)
\(
\lim _{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^x=e
\)
\(
\lim _{x \rightarrow \infty}\left(1+\frac{a}{x}\right)^x=e^a
\)
\(
\lim _{x \rightarrow 0}(1+x)^{\frac{1}{x}}=e
\)
\(
\begin{aligned}
&\lim _{x \rightarrow 0} \frac{a^x-1}{x}=\log _e a \\
&\lim _{x \rightarrow 0} \frac{\log (1+x)}{x}=1
\end{aligned}
\)
\({x}^{{n}}\) Formula:
\(
\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}=n(a)^{n-1}
\)

Limits of Exponential and Log Functions

\(\lim _{x \rightarrow 0} \sin x=0\)
\(\lim _{x \rightarrow 0} \cos x=1\)
\(\lim _{x \rightarrow 0} \frac{1-\cos x}{x}=0\)
\(\lim _{x \rightarrow 0} \frac{\sin ^{-1} x}{x}=1\)
\(\lim _{x \rightarrow 0} \frac{\tan ^{-1} x}{x}=1\)
\(\lim _{x \rightarrow 0} \frac{\sin x}{x}=1\)
\(\lim _{x \rightarrow 0} \frac{\tan x}{x}=1\)

Continuous Function

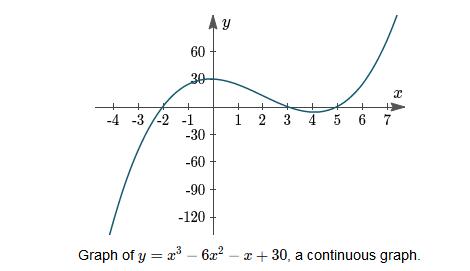
A graph for a function that’s smooth without any holes, jumps, or asymptotes is called continuous. Any value of \(x\) will give us a corresponding value of \(y\). We could continue the graph in the negative and positive directions, and we would never need to take the pencil off the paper. Such functions are called continuous functions.

For example, Consider the graph of \(f(x)=x^3-6 x^2-x+30\)

Discontinuous Function

A function that is not continuous at an \(x\) value either has a removable discontinuity (a hole in the graph of the function) or a nonremovable discontinuity (such as a jump or an asymptote in the graph) is known as a discontinuous function.

For example, consider the function and its waveform below.

Now consider the function \(f(x)=\frac{1}{x-1}\).
We note that the curve is not continuous at \(x=1\).

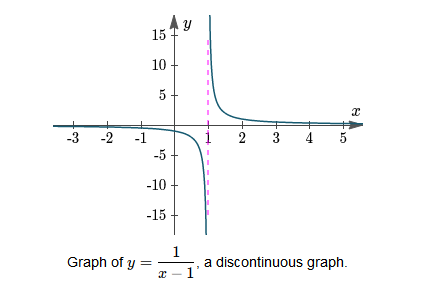
We observe that a small change in \(x\) near \(x=1\) gives a very large change in the value of the function. For a function to be continuous at a point, the function must exist at the point and any small change in \(x\) produces only a small change in \(f(x)\).

How to Check the Existence of a Limit

The limit of a function \(f(x)\) exists if and only if the one-sided limits of the function are equal.
\(\lim _{x \rightarrow a} f(x)=L \quad\) if and only if \(\lim _{x \rightarrow a^{-}} f(x)=\lim _{x \rightarrow a^{+}} f(x)=L\)

For example, to check whether the limit exists for the function \(f(x)\) at \(x=a\),We have to check, if
Left hand side limit \(=\) Right Hand side limit \(=f(a)\)
That is \(\lim _{x \rightarrow a^{-}} f(x)=\lim _{x \rightarrow a^{+}} f(x)=f(a)\)

Let’s look at the example below and find out how to solve a limit graphically by investigating some one-sided and two-sided limits.

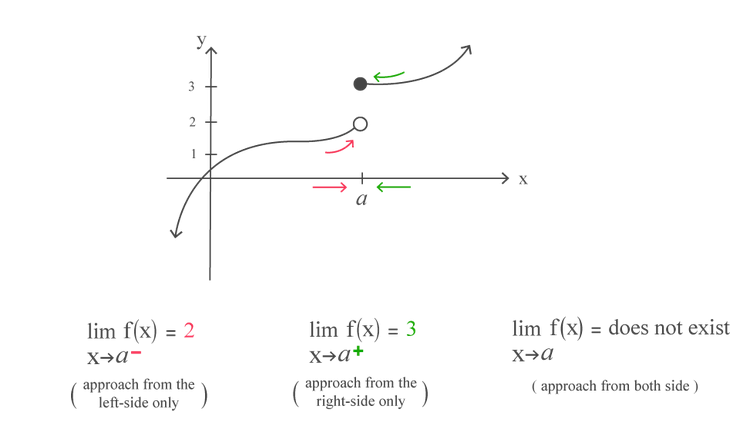
Because the limit (i.e., y-value) gets closer to two different values as we approach a from either side of “a”, we can’t make up our mind as to what our limit should be, therefore, we say that the limit does not exist.

Consequently, a limit only exists if and only if the limit from the left side equals the limit from the right side.

\(\lim _{x \rightarrow a} f(x)=L \text { if and only if } \lim _{x \rightarrow a^{-}} f(x)=\lim _{x \rightarrow a^{+}} f(x)\)

Continuity

A function \(f(x)\) is continuous at \(a\) when the following three conditions are met:

• \(f(a)\) is defined
• \(\lim _{x \rightarrow a} f(x)\) exists
• \(\lim _{x \rightarrow a^{+}} f(x)=\lim _{x \rightarrow a^{-}} f(x)=f(a)\)

Informally, if you can sketch a graph without lifting your pencil off the paper, then we say that function is continuous. Otherwise, we declare a function is discontinuous.

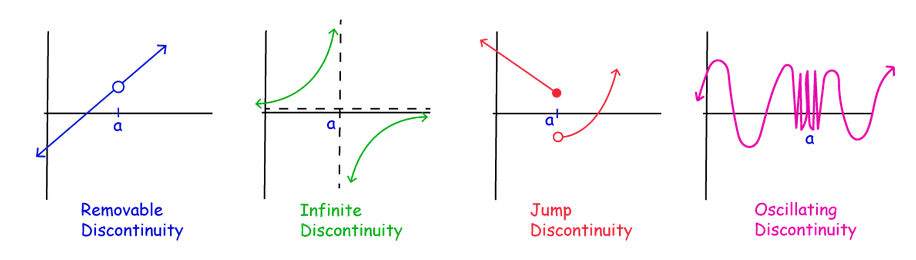
There are four types of discontinuity(shown in the figure below):

1. Removable Discontinuity: In removable discontinuity, a function which has well- defined two-sided limits at \(x=a\), but either \(f(a)\) is not defined or \(f(a)\) is not equal to its limits. The removable discontinuity can be given as:
   \(
   \lim _{x \rightarrow a} f(x) \neq f(a)
   \)
2. InfiniteDiscontinuity: In infinite discontinuity, the function diverges at \(x=\) a to give a discontinuous nature. It means that the function \(f(a)\) is not defined. Since the value of the function at \(x=\) a does not approach any finite value or tends to infinity, the limit of a function \(x \rightarrow a\) are also not defined.
3. Jump Discontinuity: Jump Discontinuity is a type of discontinuity, in which the left-hand limit and right-hand limit for a function \(x=a\) exists, but they are not equal to each other. The jump discontinuity can be represented as:
   \(
   \lim _{x \rightarrow a^{+}} f(x) \neq \lim _{x \rightarrow a^{-}} f(x)
   \)
4. Oscillating Discontinuity: An oscillating discontinuity exists when the values of the function appear to be approaching two or more values simultaneously. A standard example of this situation is the function \(f(x)=\sin \left(\frac{1}{x}\right)\), pictured below.

This is shown in the waveform below.

Example 6: Is the function \(f(x)=\frac{x^2-2 x}{x-3}\) continuous at \(x = 4\)?

Solution:

\(f(x)=\frac{x(x-2)}{x-3}\)
\(\lim _{x \rightarrow 4} f(x) = 8\)
\(f(4) = 8\)
As \(f(4)=\lim _{x \rightarrow 4} f(x)\)
Since both sides of the equation are 8, \(\text { so } f(x) \text { is continuous at } x=4 \text {. }
\)

Example 7: Given the function
\(f(x)= \begin{cases}7-4 x & x<1 \\ x^2+2 & x \geq 1\end{cases}\)
Evaluate the following limit, if they exist.

\(\lim _{x \rightarrow 1} f(x)\)

Solution: 

We are looking at the limit at \(x=1\) and that is the “cut-off” point in the piecewise functions. Recall from the discussion in the section, that this means that we are going to have to look at the two one-sided limits.
\(
\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{-}}(7-4 x)=\underline{3} \quad \text { because } x \rightarrow 1^{-} \text {implies that } x<1
\)
\(\lim _{x \rightarrow 1^{+}} f(x)=\lim _{x \rightarrow 1^{+}}\left(x^2+2\right)=\underline{3} \quad\) because \(x \rightarrow 1^{+}\)implies that \(x>1\)
So, in this case, we can see that,
\(
\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{+}} f(x)=3
\)
and so we know that the overall limit must exist and,
\(
\lim _{x \rightarrow 1} f(x)=3
\)

Example 8: Determine the existence of \(\lim _{x \rightarrow 7} f(x)\) given
\(f(x)= \begin{cases}13 x+7 & \text { if } 1<x<7 \\ 14 x+7 & \text { if } 7 \leq x<8\end{cases}\)

Solution: 

Since this is a piecewise-defined function and \(x=7\) is on the boundary of two subdomains, we cannot evaluate this limit by direct substitution. Instead, we recall that we can determine the limit of this function as \(x\) approaches 7 by checking that the left and right limits of \(f(x)\) exist and are equal.

We start with \(\lim _{x \rightarrow 7^{-}} f(x)\), since this is a left limit; we have \(x<7\) for our input values and when evaluating this limit the values of \(x\) will get arbitrarily close to 7 , so we can assume \(1<x<7\), without affecting the value of the limit. When our values of \(x\) are in this interval, \(f(x)=13 x+7\), this gives us
\(
\lim _{x \rightarrow 7^{-}} f(x)=\lim _{x \rightarrow 7^{-}}(13 x+7) .
\)
We can evaluate this by direct substitution:
\(
\lim _{x \rightarrow 7^{-}}(13 x+7)=13(7)+7=98 .
\)
We can do the same for the right limit; restricting the values of \(x\) to be in the interval \([ 7,8]\) does not affect the value of the limit, giving us
\(
\begin{aligned}
\lim _{x \rightarrow 7^{+}} f(x) &=\lim _{x \rightarrow 7^{+}}(14 x+7) \\
&=14(7)+7 \\
&=105.
\end{aligned}
\)
For the limit of \(f(x)\) at \(x=7\) to exist, both the left and right limits need to be equal. However, we have shown that they are not equal.
Hence, the limit does not exist because \(\lim _{x \rightarrow 7^{-}} f(x) \neq \lim _{x \rightarrow 7^{+}} f(x)\).

Example 9: Find \(\lim _{x \rightarrow-9} f(x)\), where \(f(x)= \begin{cases}-8+|x+9|, & x \neq-9 \\ -7, & x=-9\end{cases}
\)

Solution: Since this is a piecewise-defined function and \(x=-9\) is on the boundary of two subdomains, we cannot evaluate this limit by direct substitution. Instead, we recall that we can determine the limit of this function as \(x\) approaches \(-9\) by checking that the left and the right limit of \(f(x)\) exist and are equal.
We will start with \(\lim _{x \rightarrow-9^{+}} f(x)\). When \(x>-9\), we know that \(|x+9|=x+9\), so
\(
\begin{aligned}
-8+|x+9| &=-8+x+9 \\
&=x+1
\end{aligned}
\)
Therefore, when \(x>-9\), we have \(f(x)=x+1\); this means that their limits as \(x\) approaches \(-9\) from the right must be equal, giving us
\(
\begin{aligned}
\lim _{x \rightarrow-9^{+}} f(x) &=\lim _{x \rightarrow-9^{+}}(-8+|x+9|) \\
&=\lim _{x \rightarrow-9^{+}}(x+1) \\
&=-9+1 \\
&=-8.
\end{aligned}
\)
Similarly, when \(x<-9\), we have \(-8+|x+9|=-8-(x+9)=-x-17\). This means
\(
\begin{aligned}
\lim _{x \rightarrow-9^{-}} f(x) &=\lim _{x \rightarrow-9^{-}}(-8+|x+9|) \\
&=\lim _{x \rightarrow-9^{-}}(-x-17) \\
&=-(-9)-17 \\
&=-8.
\end{aligned}
\)
Since the left and the right limit of \(f(x)\) both exist and are equal to \(-8\), we can conclude that
\(
\lim _{x \rightarrow-9} f(x)=-8
\)

Example 10: Determine the existence of \(\lim _{x \rightarrow 2} \frac{1}{|x-2|} \text {. }\)

Solution:

We recall that we can determine the limit of this function as \(x\) approaches 2 by checking that the left and the right limits of \(f(x)\) at \(x=2\) exist and are equal. To determine the value of this limit, we can sketch a graph of \(y=\frac{1}{|x-2|}\). First, we can sketch \(y=\frac{1}{x-2}\) as a translation of \(y=\frac{1}{x}\) two units to the right, then we notice that \(\frac{1}{|x-2|}=\left|\frac{1}{x-2}\right|\), so we reflect the negative parts of the curve in the \(x\)-axis, giving us the following. The graph will have a vertical asymptote at \(x=2\). If we look at the outputs of the function to the left and right of \(x=2\), we can see that as the values of \(x\) approach 2 from either side, the outputs of the function will grow without bound.

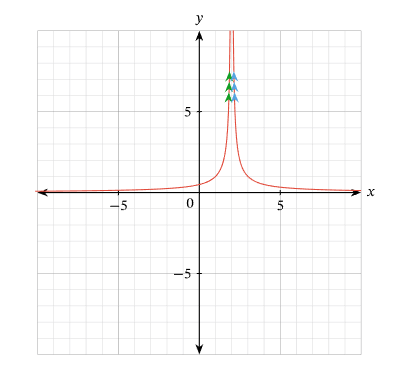
In terms of limits, this tells us
\(
\lim _{x \rightarrow 2^{+}} \frac{1}{|x-2|}=\infty \quad \text { and } \quad \lim _{x \rightarrow 2^{-}} \frac{1}{|x-2|}=\infty
\)
Recall that saying a limit is equal to infinity means that the limit does not exist. However, since the left and right limits agree, we can say that \(\lim _{x \rightarrow 2} \frac{1}{|x-2|}=\infty\).
Hence, \(\lim _{x \rightarrow 2} \frac{1}{|x-2|}\) does not exist, but \(\lim _{x \rightarrow 2} \frac{1}{|x-2|}=\infty\).

Example 11: Understanding Limits and Oscillating Behavior

Investigate the behavior of \(\lim _{x \rightarrow-0}f(x)=\lim _{x \rightarrow-0}[2 \cos \left(\frac{1}{x}\right)]\)

1. Complete the table of values of \(f(x)\) for values of \(x\) that get closer to 0 .

2. What does this suggest about the graph of \(f\) close to 0?
a. That it increases without bound
b. That it decreases without bound
c. That it changes randomly
d. That it approaches 2
e. That it oscillates rapidly between \(-2\) and 2

3. Hence, evaluate \(\lim _{x \rightarrow 0} f(x)\).

Solution:

Part 1:
We find each entry in the table by substituting the given value of \(x\) into the function \(f(x)=2 \cos \left(\frac{1}{x}\right)\). For example,
\(
\begin{aligned}
f\left(\frac{1}{99 \pi}\right) &=2 \cos \left(\frac{1}{\left(\frac{1}{99 \pi}\right)}\right) \\
&=2 \cos (99 \pi)
\end{aligned}
\)
The cosine function is periodic with a period of \(2 \pi\), so we can simplify
\(
\begin{aligned}
2 \cos (99 \pi) &=2 \cos (98 \pi+\pi) \\
&=2 \cos (\pi) \\
&=-2
\end{aligned}
\)
Similarly,
\(
\begin{aligned}
f\left(\frac{1}{100 \pi}\right) &=2 \cos \left(\frac{1}{\left(\frac{1}{100 \pi}\right)}\right) \\
&=2 \cos (100 \pi) \\
&=2 \cos 0 \\
&=2.
\end{aligned}
\)
We can follow this process for all of the entries in the table to get the following.

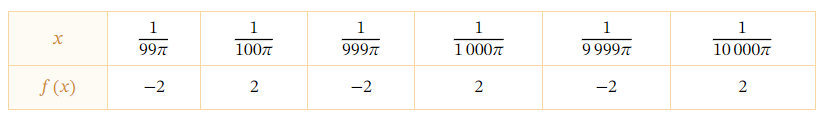
Part 2:
In the table, we can see that, from left to right, the values of \(x\) approach 0. However, the outputs of the function do not approach any value; instead, the outputs oscillate between \(-2\) and 2.
Therefore, the table suggests that the graph rapidly oscillates between \(-2\) and 2, which is an option \(\mathrm{E}\).

Part 3:
The table in part 1 suggests that \(f(x)\) does not converge to any value; instead, the outputs oscillate between \(-2\) and 2 . This means that the right limit of \(f(x)\) at \(x=0\) does not exist. For the limit of \(f(x)\) at \(x=0\) to exist, we need both the left and the right limit to exist and be equal.
Hence, the limit does not exist.

Properties of Limits

Let \(f(x)\) and \(g(x)\) be two functions and a be a value such that
\(
\begin{aligned}
&\lim _{x \rightarrow a} f(x) &\text { and } &\lim _{x \rightarrow a} g(x) &\text { exists.}
\end{aligned}
\)

1. Sum Rule: This rule states that the limit of the sum of two functions is equal to the sum of their limits

\(\lim _{x \rightarrow a}[f(x)+g(x)]=\lim _{x \rightarrow a} f(x)+\lim _{x \rightarrow a} g(x)\)

Example 12: Evaluate \(\lim _{x \rightarrow \pi / 4}[\sin (x)+\cos (x)]\)

Solution:

\(
\lim _{x \rightarrow \pi / 4}[\sin (x)+\cos (x)]=\lim _{x \rightarrow \pi / 4} \sin (x)+\lim _{x \rightarrow \pi / 4} \cos (x)
\) \(
=\sin \left(\frac{\pi}{4}\right)+\cos \left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}=\sqrt{2}
\)

2. Difference Rule: This rule states that the limit of the difference of two functions is equal to the difference of their limits.

\(\lim _{x \rightarrow a}[f(x)-g(x)]=\lim _{x \rightarrow a} f(x)-\lim _{x \rightarrow a} g(x)\)

Example 13: Evaluate \(\lim _{x \rightarrow \frac{1}{2}}(x-9)\)

Solution: 

\(
\begin{aligned}
\lim _{x \rightarrow \frac{1}{2}}(x-9) &=\lim _{x \rightarrow \frac{1}{2}} x-\lim _{x \rightarrow \frac{1}{2}} 9 \\
&=\frac{1}{2}-9 \\
&=\frac{1}{2}-\frac{18}{2} \\
&=-\frac{17}{2}
\end{aligned}
\)

3. Constant Multiple Rule: The limit of a constant times a function is equal to the product of the constant and the limit of the function.

For every real number \(c\), \(\lim _{x \rightarrow a}[c f(x)]=c \lim _{x \rightarrow a} f(x) \\\)

Example 14: \(\lim _{x \rightarrow 3}(8 x)\)

Solution: 

\(
\begin{aligned}
\lim _{x \rightarrow 3}(8 x) &=8 \lim _{x \rightarrow 3} x \\
&=8(3) \\
&=24
\end{aligned}
\)

4. Product Rule: This rule says that the limit of the product of two functions is the product of their limits (if they exist).

\(\lim _{x \rightarrow a}[f(x) g(x)]=\lim _{x \rightarrow a} f(x) \times \lim _{x \rightarrow a} g(x)\)

Example 15: Evaluate \(\lim _{x \rightarrow 2} x e^x\)

Solution:

\(\lim _{x \rightarrow 2} x e^x=\lim _{x \rightarrow 2} x \cdot \lim _{x \rightarrow 2} e^x=2 e^2\)

5. Quotient Rule: The limit of the quotient of two functions is the quotient of their limits, provided that the limit in the denominator function is not zero.

\(\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}\), \(
\text { if } \lim _{x \rightarrow a} g(x) \neq 0\)

Example 16: Evaluate \(\lim _{x \rightarrow 1} \frac{\ln (x)}{x}\)

Solution:

\(\lim _{x \rightarrow 1} \frac{\ln (x)}{x}=\frac{\lim _{x \rightarrow 1} \ln (x)}{\lim _{x \rightarrow 1} x}\) \(=\frac{\ln (1)}{1}=0\)

6. Power Rule: 

\(
\lim _{x \rightarrow a}[f(x)]^p=\left[\lim _{x \rightarrow a} f(x)\right]^p
\)
where the power \(p\) can be any real number. In particular,
\(
\lim _{x \rightarrow a} \sqrt[p]{f(x)}=\sqrt[p]{\lim _{x \rightarrow a} f(x)}
\)
If \(f(x)=x^n\), then
\(
\lim _{x \rightarrow a} x^n=a^n, n=0, \pm 1, \pm 2, \ldots \quad \text { and } a \neq 0, \text { if } n \leq 0
\)

Example 17: Evaluate \(\lim _{x \rightarrow 0}[\cos (x)]^3\)

Solution:

\(
\lim _{x \rightarrow 0}[\cos (x)]^3=\left[\lim _{x \rightarrow 0} \cos (x)\right]^3=[\cos (0)]^3=1^3=1
\)

Example 18: Evaluate \(\lim _{x \rightarrow-2} \sqrt{x+18}\)

Solution:

\(
\begin{aligned}
\lim _{x \rightarrow-2} \sqrt{x+18} &=\sqrt{\lim _{x \rightarrow-2}(x+18)} \\
&=\sqrt{\lim _{x \rightarrow-2} x+\lim _{x \rightarrow-2} 18} \\
&=\sqrt{-2+18} \\
&=\sqrt{16} \\
&=4
\end{aligned}
\)

7. Limit of an exponential function: 

\(\lim _{x \rightarrow a} b^{f(x)}=b^{\lim _{x \rightarrow a} f(x)}\)
where the base \(b>0\).

Example 19: Evaluate \(\lim _{x \rightarrow 3} e^{\cos (\pi x)}\)

Solution: 

\(
\begin{aligned}
\lim _{x \rightarrow 3} e^{\cos (\pi x)} &=e^{\lim _{x \rightarrow 3} \cos (\pi x)} \\
&=e^{\cos \left(\lim _{x \rightarrow 3}(\pi x)\right)} \\
&=e^{\cos \left(\pi \lim _{z \rightarrow 3} x\right)} \\
&=e^{\cos (\pi(3))} \\
&=e^{\cos (3 \pi)} \\
&=e^{-1} \\
&=\frac{1}{e}
\end{aligned}
\)

8. Limit of a Logarithm of a function:

\(\lim _{x \rightarrow a}\left[\log _b f(x)\right]=\log _b\left[\lim _{x \rightarrow a} f(x)\right]\)
where the base \(b>0\).

Example 20: \(\text { Evaluate } \lim _{x \rightarrow 1} \log (x+1)\)

Solution:

We first put \(x=1\) in \(\log (x+1)\)
\(\therefore \lim _{x \rightarrow 1} \log (x+1)=\log (1+1)\)
\(=\log 2\)

Example 21: Evaluate \(\lim _{x \rightarrow 0} \frac{\log \left(1+x^3\right)}{\sin ^3 x}\)

Solution: 

Multiplying and dividing by the cube of \(x\), We can rewrite the expression as, \(\lim _{x \rightarrow 0} \frac{\log \left(1+x^3\right)}{x^3} \times \frac{x^3}{\sin ^3 x}\)

Now, using the property of a limit, \(\lim _{x \rightarrow 0} \frac{\log (1+x)}{x}=1\) (\(
\log _e(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\ldots \ldots \ldots \infty
\))
And, \(\lim _{x \rightarrow 0} \frac{\sin x}{x}=1\)

\(\text { Answer }=1 \times 1=1\)

9. The Squeeze Theorem:

Suppose that \(g(x) \leq f(x) \leq h(x)\) for all \(x\) close to \(a\), except perhaps for \(x=a\). If
\(
\lim _{x \rightarrow a} g(x)=\lim _{x \rightarrow a} h(x)=L,
\)
then
\(
\lim _{x \rightarrow a} f(x)=L .
\)
The idea here is that the function \(f(x)\) is squeezed between two other functions having the same limit \(L\).

Example 22: What is the value of the limit \(\lim _x \rightarrow_0 x^2 \sin (1 / x)?\)

Solution:

We know that \(-1 \leq \sin x \leq 1\) for any \(x\). In the same way \(-1 \leq \sin (1 / x) \leq 1(\) when \(x \neq 0)\)
Multiplying each side by \(x^2\) (This does not change the sign of inequality as \(x^2 \geq 0\) ):
\(-x^2 \leq \sin (1 / x) \leq x^2\)
Now, \(\lim _x \rightarrow_0-x^2=-0^2=0\) and \(\lim _{x \rightarrow 0} x^2=\lim _x \rightarrow_0 0^2=0\)
So by sandwich theorem, \(\lim _x \rightarrow_0 x^2 \sin (1 / x)=0\).