Kinematics is a mathematical branch of physics that uses equations to describe the motion of objects (specifically ​trajectories​) without referring to forces.

Kinematics is simply the study of motion. This is literally what the word means: kinesis (motion) + tics (the study of). On a more practical level, the kinematics you learn in your intro physics class is the study of position, velocity, and momentum. On the most practical level, kinematics is the study of what happens when you toss a ball. 

So kinematics is the study of three things, position, velocity and acceleration of an object.

Position tells you where an object is. It’s location. We are also often interested in the change in position, known as displacement. Velocity tells you how fast an object is moving and in what direction. Acceleration tells you how the velocity of the object is changing. If a Ferrari goes from 0 to 100 Km/hr in 2.5 seconds then it is accelerating. 

Avoid Common Mistakes: Position, Distance and Displacement

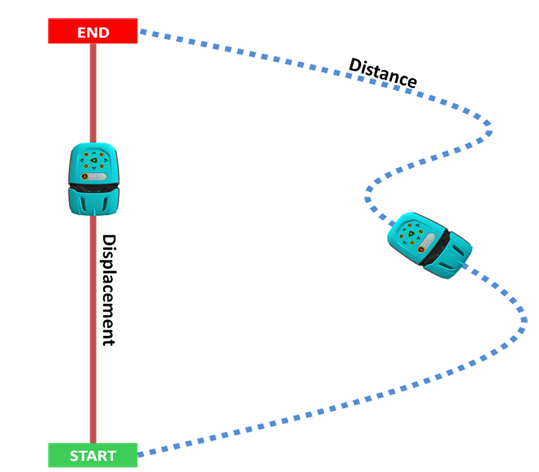
Position, Displacement and Distance are easy to confuse and physics teachers often test to make sure you understand the difference. Position is measured from some origin point and defines the location of the object – in kinematics, we often define the origin point as the starting location of the object to make things easier. Distance measures the total distance an object has traveled. Displacement measures how far an object is from where it started.

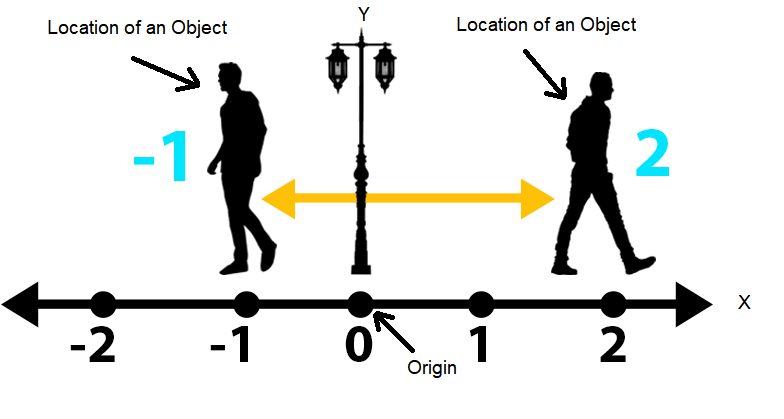
Position

Position is the place occupied by an object. It is defined relative to a reference point. When an object changes its position, motion occurs. The positive direction for motion must always be indicated. Position is a point in space, is determined by its distance and direction from other points. The statement of position is accomplished by means of a frame of reference or a point of reference, which is called the Origin. Position is a location of a point using rectangular coordinates, \(x\) and \(y\) axes. When writing the coordinates of points, \({x}\) is written first followed by \({y}\).

Point object

An object is considered as point object, if the size of the object is much smaller than the distance, it moves in a reasonable duration of time. e.g. Earth can be considered as a point object during its revolution around the sun because it covers much larger distance than its own size.

What Is Distance?

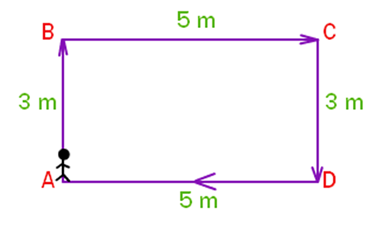
Distance is the actual path length that an object moves away from its original position. Distance is a scalar. If an object moves from A position to B, then to point C, then to point D and back to point A as shown in Fig below, the total distance covered by the object is equal to 3 m + 5 m + 3 m + 5 m = 16 m. The unit of distance is metre in SI or MKS and centimetre in CGS. Its dimensional formula is \(\left[\mathrm{M}^0 \mathrm{LT}^0\right]\).

What is Displacement?

Displacement is defined as the change in position of an object. It is a vector quantity and has a direction and magnitude. It is represented as an arrow that points from the starting position to the final position. For example- If an object moves from A position to B, then the object’s position changes. This change in the position of an object is known as Displacement (displacement is the minimum distance directed from initial position to the final position).

\(
\begin{array}{l}
\text { Displacement } = \Delta x=x_f-x_i \\
x_f=\text { Final Position of the object } \\
x_i=\text { Initial Position the object } \\
\Delta x=\text { Displacement }
\end{array}
\)

• If \(x_f>x_i\), then \(\Delta x\) is positive.
• If \(x_f<x_i\), then \(\Delta x\) is negative.
• If \(x_f=x_i\), then \(\Delta x\) is zero.

i.e. The displacement of an object in motion can be positive, negative or zero while distance can never be negative or zero.
Displacement has both magnitude and direction. The unit of displacement is metre in SI or MKS and centimetre in CGS. Its dimensional formula is \(\left[\mathrm{M}^0 \mathrm{LT}^0\right]\).
To understand distance and displacement clearly, let us consider the following example:

Suppose a person (moving body) moves from \(A\) to \(B(4 \mathrm{~km})\) towards east and from \(B\) to \(C(3 \mathrm{~km})\) due north as shown in figure, then the distance travelled by the person is
\(
A B+B C=4 \mathrm{~km}+3 \mathrm{~km}=7 \mathrm{~km}
\)

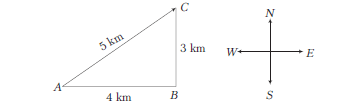
But the displacement of the person is \(A C\) which can be calculated by Pythagoras’ theorem,
\(
\begin{aligned}
A C^2 & =A B^2+B C^2 \\
& =(4)^2+(3)^2=16+9=25 \\
\Rightarrow \quad A C & =5 \mathrm{~km}
\end{aligned}
\)

Example 1: Problem 2: An object moves along a right triangle from point A to B to C shown in the figure below. (Consider the sides as \(3 \mathrm{~m}\) and \(4 \mathrm{~m}\) )
(a) Find the magnitude and direction of the displacement vector?
(b) How much distance is traveled by this moving object?
(c) Suppose the object returns to point A, its initial position. Now, Find the displacement and distance.

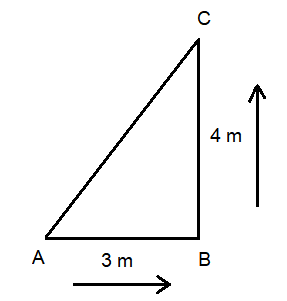
Answer: (a) Connect the initial (A) and final (C) points together by the straightest line. The magnitude and direction of that line represent the displacement vector. Here, the displacement is the hypotenuse of the right triangle. So using the Pythagorean theorem, one finds its magnitude as
\(
\begin{aligned}
c^2 & =a^2+b^2 \\
\Rightarrow c & =\sqrt{a^2+b^2} \\
& =\sqrt{3^2+4^2}=5 \mathrm{~m}
\end{aligned}
\)
the direction of displacement is shown in figure (to the north-east).

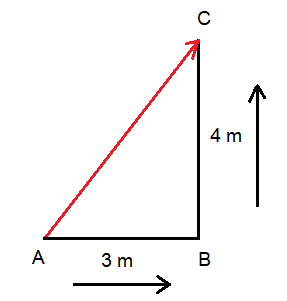
(b) Adding the base and height of this triangle gets the distance traveled from (A) to (C).
\(
\begin{aligned}
& =3 ~m +4 ~m \\
& =7 {~m}
\end{aligned}
\)
(c) Displacement is zero since the object returns to the initial position (\(x_f = x_i\)). \(\text { Displacement } = \Delta x=x_f-x_i = 0\). Distance is also computed as the perimeter of the triangle. In this case it is \(3 ~m + 4 ~m + 7 ~m = 14 ~m\).

Distance versus Displacement

• The magnitude of displacement may or may not be equal to the distance traversed by an object.
• The magnitude of the displacement for a course of motion may be zero but the corresponding distance can never be zero.
• If a particle moves in a straight line without change in direction, the magnitude of displacement is equal to the distance travelled otherwise displacement is always less than distance. Thus, \(\mid\) Displacement \(\mid \leq\) Distance
• Distance depends on the path while displacement is independent of the path but depends only on initial and final positions.

Avoid Common Mistakes: Velocity and Speed

Speed is a scalar quantity that refers to “how fast an object is moving.” Speed can be thought of as the rate at which an object covers distance. A fast-moving object has a high speed and covers a relatively large distance in a short amount of time. Contrast this to a slow-moving object that has a low speed; it covers a relatively small amount of distance in the same amount of time. An object with no movement at all has a zero speed.

Velocity is speed with a direction (a vector quantity), that is how fast it moves and in what direction (we call this concept of magnitude+direction a vector). That means an object can change velocity without changing speed, for examples a car going around a circular track. It also means that speed can increase while velocity decreases. If velocity is negative and acceleration is negative then the velocity will be a more and more negative number, so velocity will decrease (go from \(-60 \mathrm{~m} / \mathrm{s}\) to -120 \(\mathrm{m} / \mathrm{s}\) ) but speed will increase (go from \(60 \mathrm{~m} / \mathrm{s}\) to \(120 \mathrm{~m} / \mathrm{s}\) ).

Saying Ariel the Dog runs at \(\mathbf{9} \mathbf{~ k m} / \mathbf{h}\) (kilometers per hour) is a speed.
But saying he runs \(\mathbf{9} \mathbf{~ k m} / \mathbf{h}\) towards north is a velocity.

\(
\begin{array}{|l|c|c|}
\hline & \text { Speed } & \text { Velocity } \\
\hline \text { Has: } & \text { magnitude } & \begin{array}{c}
\text { magnitude and } \\
\text { direction }
\end{array} \\
\hline \text { Example: } & 60 \mathrm{~km} / \mathrm{h} & 60 \mathrm{~km} / \mathrm{h} \text { North } \\
\hline \text { Example: } & 5 \mathrm{~m} / \mathrm{s} & 5 \mathrm{~m} / \mathrm{s} \text { upwards } \\
\hline
\end{array}
\)

Avoid Common Mistakes: Acceleration and Velocity

Students new to physics are often puzzled by the idea that acceleration and velocity can go in different directions. When an object accelerates it should go faster, right? Not necessarily. For example, if you throw an object in the air, it starts with a positive, upward velocity but the acceleration is negative and downward. Eventually, the object stops going up and falls back to the ground, at which point the acceleration and the velocity are in the same direction. However, at any given moment the acceleration can be in any direction – acceleration determines the change in velocity not the velocity itself. 

Example 2: A displacement vector has a magnitude of \(810 \mathrm{~m}\), and points at an angle of \(18^{\circ}\) above the positive \({x}\)-axis. What are the \(x\) and \(y\) components of this vector?

Answer: Let’s draw the diagram as shown below from the given description of the problem.

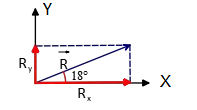
Given the length and direction of a vector such as displacement \(\vec{R}\), one can find its components by the following formulas
\(
\begin{aligned}
R_x & =|\vec{R}| \cos \theta =(810) \cos 18^{\circ}=770.35 \mathrm{~m}
\end{aligned}
\)

and
\(
\begin{aligned}
R_y & =|\vec{R}| \sin \theta =(810) \sin 18^{\circ}=250.30 \mathrm{~m}
\end{aligned}
\)

Motion in a Straight Line

Motion is defined as the change in position of an object with time. When the object moves along a single axis, the motion is known as one dimensional motion or rectilinear motion and such a motion is along a straight line only, which may be horizontal or vertical. 

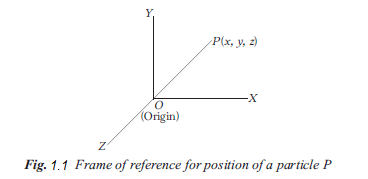
Frame of reference

A system of coordinate axes which defines the position of a particle or an event in two or three dimensional space along with a clock constitutes a frame of reference. The simplest frame of reference is the cartesian system of coordinates, in which the position of the particle \((P)\) is specified by its three coordinates \(x, y\) and \(z\).

Types of frame of reference: Frame of references are of two types

• Inertial frame of reference: It is a frame of reference, where Newton’s law holds good. e.g. An object will remains at rest or in uniform motion unless acted by an external force. An inertial frame of reference is either at rest or moving with a constant velocity.
• Non-inertial frame: of reference An accelerating frame of reference is called a non-inertial frame of reference. In this reference frame, Newton’s law will not hold true.

Rest and Motion

If the position of an object does not change with respect to time its surrounding with the passage of time, it is said to be at rest. e.g. Book lying on the table, a person sitting on a chair, etc. and if the position of an object is continuously changing with respect to its surrounding, then it is said to be in the state of motion. e.g. The man walking, a car being driven, water flowing down a dam, etc.

Rest and motion are relative terms

Rest and motion are always relative but never absolute. It means an object, can be at rest for an observer but the same object can be in motion when observed by other observer. e.g. A person sitting in his house is at rest with respect to earth but is in motion with respect to moon.

Classification of motion

On the basis of the number of coordinates required to specify the position of an object, the motion of the object can be classified as:

One dimensional motion
The motion of an object is considered as one dimensional, if only one coordinate (\(x\)) is needed to specify the position of the object.

In one dimensional motion, the object moves along a straight line. e.g. A boy running on a straight line, motion of freely falling body, etc.

Two dimensional motion

The motion of an object is considered as two dimensional, if two coordinates (\(x\) and \(y\)) are needed to specify the position of the object.

In two dimensional motion, the object moves in a plane. e.g. Motion of billiard ball.

Three dimensional motion

The motion of an object is considered as three dimensional, if all the three coordinates are needed to specify the position of the object.

In three dimensional motion, the object moves in a space. e.g. Butterfly flying in garden, the motion of water molecules, etc.

Displacement in terms of Position Vector

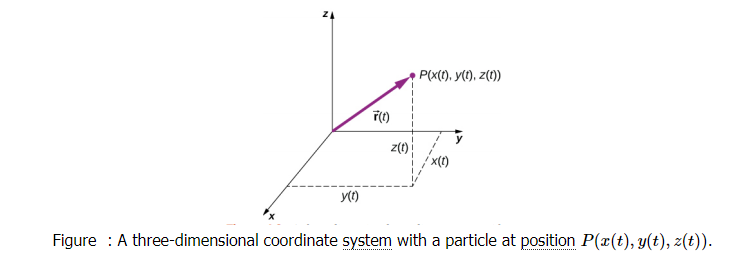
To describe motion in two and three dimensions, we must first establish a coordinate system and a convention for the axes. We generally use the coordinates \(x, y\), and \(z\) to locate a particle at point \(P(x, y, z)\) in three dimensions. If the particle is moving, the variables \(x, y\), and \(z\) are functions of time \((t)\) :
\(
x=x(t) \quad y=y(t) \quad z=z(t) .
\)

The position vector from the origin of the coordinate system to point \(\mathrm{P}\) is \(\vec{r}(t)\). In unit vector notation, introduced in Coordinate Systems and Components of a Vector, \(\vec{r}(\mathrm{t})\) is
\(
\vec{r}(t)=x(t) \hat{i}+y(t) \hat{j}+z(t) \hat{k} .
\)

Figure below shows the coordinate system and the vector to point \(P\), where a particle could be located at a particular time \(t\). Note the orientation of the \(\mathrm{x}, \mathrm{y}\), and \(\mathrm{z}\) axes.

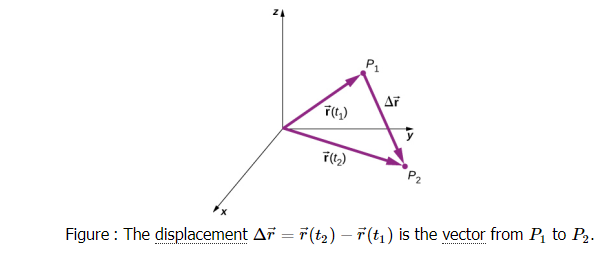
With our definition of the position of a particle in three-dimensional space, we can formulate the three-dimensional displacement. Figure below shows a particle at time \(t_1\) located at \(P_1\) with position vector \(\vec{r}\left(t_1\right)\). At a later time \(t_2\), the particle is located at \(P_2\) with position vector \(\vec{r}\left(t_2\right)\). The displacement vector \(\Delta \vec{r}\) is found by subtracting \(\vec{r}\left(t_1\right)\) from \(\vec{r}\left(t_2\right)\) :
\(
\Delta \vec{r}=\vec{r}\left(t_2\right)-\vec{r}\left(t_1\right)
\)

Vector addition is discussed in Vectors. Note that this is the same operation we did in one dimension, but now the vectors are in three-dimensional space.

The displacement vector from the point \(P_1=\left(x_1, y_1, z_1\right)\) to the point \(P_2=\left(x_2, y_2, z_2\right)\) is given in components by
\(
\Delta \vec{r}=\overrightarrow{P_1 P_2}=\left(x_2-x_1\right) \hat{i}+\left(y_2-y_1\right) \hat{j}+\left(z_2-z_1\right) \hat{k}
\)

The distance \(d=|\Delta \vec{r}|=\) between points \(\left(x_1, y_1, z_1\right)\) and \(\left(x_2, y_2, z_2\right)\) is given by the formula
\(
d=|\Delta \vec{r}|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2} .
\)

Example 3: Find the distance between points \(P_1=(3,-1,5)\) and \(P_2=(2,1,-1)\) and the displacement vector.

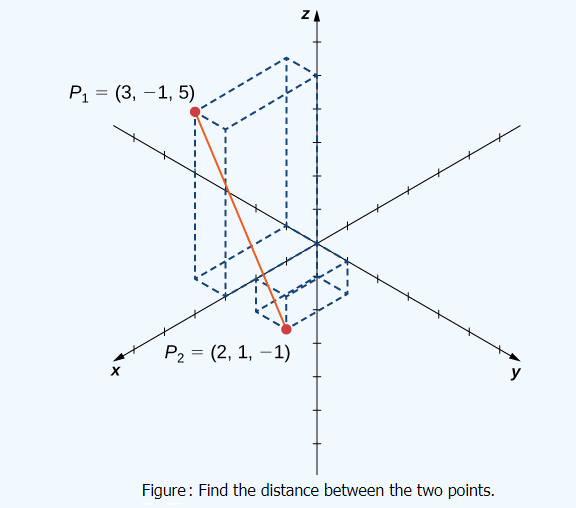
Answer:The Displacement vector is given by

\(
\overrightarrow{P_1 P_2}=\left(x_2-x_1\right) \hat{i}+\left(y_2-y_1\right) \hat{j}+\left(z_2-z_1\right) \hat{k}
\)

The distance can be calculated taking magnitude of the displacement vector

\(
\begin{aligned}
d\left(P_1, P_2\right) & =|{\overrightarrow{P_1 P_2}}|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2} \\
& =\sqrt{(2-3)^2+(1-(-1))^2+(-1-5)^2} \\
& =\sqrt{(-1)^2+2^2+(-6)^2} \\
& =\sqrt{41} .
\end{aligned}
\)

Example 4: A wheel completes 2000 revolutions to cover the \(9.5 \mathrm{~km}\) distance. Find the diameter of the wheel.

Answer: Given, number of revolutions, \(n=2000\)
Distance, \(x=9.5 \mathrm{~km}=9.5 \times 10^3 \mathrm{~m}=9500 \mathrm{~m}\)
\(\because\) Distance covered in \(n\) revolutions is equal to the circumference of the wheel,
\(
\begin{array}{l}
x=n \cdot 2 \pi r \Rightarrow x=n \cdot \pi D \quad(\because \text { Diameter }=2 \times \text { Radius }) \\
9500=2000 \times \pi \times D
\end{array}
\)

Example 5: A man starts from his home and walks \(50 \mathrm{~m}\) towards north, then he turns towards east and walks \(40 \mathrm{~m}\) and then reaches to his office after moving \(20 \mathrm{~m}\) towards south.
(a) What is the total distance covered by the man from his home to office?
(b) What is his displacement from his home to office?

Answer: Let \(O\) represents the position of home, then according to the question, the man moves from \(O\) to \(A(50 \mathrm{~m})\) towards north, then from \(A\) to \(B(40 \mathrm{~m})\) towards east and from \(B\) to \(C(20 \mathrm{~m})\) towards south as shown in figure.

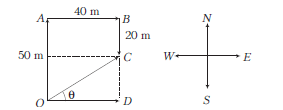
(i) Total distance travelled by the man is
\(
O A+A B+B C=50+40+20=110 \mathrm{~m}
\)
(ii) Displacement of the person is \(O C\), which can be calculated by Pythagoras theorem, i.e.
\(
\begin{aligned}
O C^2 & =O D^2+C D^2=(40)^2+(30)^2 \\
& =1600+900=2500 \\
\Rightarrow \quad O C & =50 \mathrm{~m}
\end{aligned}
\)

Example 6: An object covers \((1 / 4)\) th of the circular path What will be the ratio of the distance and displacement of the object?

Answer:Distance covered by object \(=1 / 4\) th of the circular path
\(
\begin{array}{l}
=A B \text { through path (1) } \\
=1 / 4 \text { th of circumference of circular path }=\frac{2 \pi r}{4}=\frac{\pi r}{2}
\end{array}
\)

\(
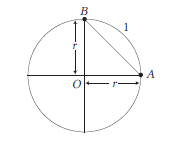
\begin{array}{l}
\text { Displacement }=\text { Shortest distance between initial position }(A) \\
\text { and final position }(B) \\
\qquad A B=\sqrt{O A^2+O B^2}=\sqrt{r^2+r^2}=r \sqrt{2} \\
\therefore \frac{\text { Distance }}{\text { Displacement }}=\frac{\pi r / 2}{r \sqrt{2}}=\frac{\pi}{2 \sqrt{2}}
\end{array}
\)

Example 7: Displacement of a person moving from \(X\) to \(Y\) along a semicircular path of radius \(r\) is \(200 \mathrm{~m}\). What is the distance travelled by him?

Answer: Given, displacement \(=200 \mathrm{~m}\)
Distance travelled by the person from \(X\) to \(Y\) is equal to the circumference of the semicircular path,
\(
x=\frac{\pi D}{2} \Rightarrow x=\pi r \quad(\because \text { Diameter }=2 \times \text { Radius }) . .(\text { (i) }
\)
According to the question, the shortest distance between the final position \(Y\) and initial position \(X\) is \(X Y=2 r\).

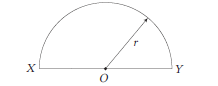
\(\therefore\) The displacement traversed by the person is \(2 r\).
\(
200=2 r \Rightarrow r=100 \mathrm{~m}
\)

Putting \(r=100 \mathrm{~m}\) in Eq. (i), we get
Distance, \(x=\pi \times 100=3.14 \times 100 \Rightarrow x=314 \mathrm{~m}\)

Example 8: An athlete completes one round of a circular track of diameter \(200 \mathrm{~m}\) in \(40 \mathrm{~s}\). What will be the distance covered and the displacement at the end of \(2 \min 20 s\) ?

Answer:Diameter of circular track, \(D=200 \mathrm{~m}\) Circumference of circular track
\(
\begin{array}{l}
=2 \pi r=\pi \times(D) \\
=\frac{22}{7} \times 200=\frac{4400}{7} \mathrm{~m}
\end{array}
\)
Time taken by athlete for completing one round \(=40 \mathrm{~s}\)
In \(40 \mathrm{~s}\), distance covered by athlete
\(
=\frac{4400}{7} \mathrm{~m}
\)
\(\therefore\) Distance covered by athlete in \(2 \mathrm{~min}\) and \(20 \mathrm{~s}(=140 \mathrm{~s}\) )
\(
=\frac{4400}{7} \times \frac{140}{40}=2200 \mathrm{~m}
\)

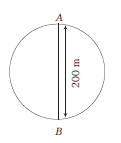
As the athlete returns to the initial point \(A\) in \(40 \mathrm{~s}\), so his displacement \(=0\)
In \(40 \mathrm{~s}\), the number of round, around the track \(=1\)
\(\therefore\) In \(140 \mathrm{~s}\), the number of rounds around the track
\(
=\frac{140}{40}=3 \frac{1}{2}
\)

For each complete round, the displacement is 0 .
\(\therefore\) For 3 complete rounds, the displacement will be 0 . Hence, the final displacement will be due to \(1 / 2\) round. Thus, his displacement \(=\) diameter of circular track \(=200 \mathrm{~m}\) \(\therefore\) Displacement after \(2 \mathrm{~min} 20 \mathrm{~s}=200 \mathrm{~m}\)

Speed

The time rate of distance travelled by an object in any direction is called speed of the object.
\(
\text { Speed }(v)=\frac{\text { Distance travelled }}{\text { Time taken }}
\)
Speed is a scalar quantity. The unit of speed in SI or MKS system is \(\mathrm{ms}^{-1}\) and in CGS system is \(\mathrm{cms}^{-1}\). Its dimensional formula is \(\left[\mathrm{M}^0 \mathrm{LT}^{-1}\right]\).
For a moving body, speed is always positive and can never be negative or zero.

Average Speed

The ratio of the total distance travelled by the object to the total time taken is called average speed of the object.
\(
\text { i.e. } \text { Average speed }=\frac{\text { Total distance travelled }}{\text { Total time taken }}
\)

For example, A car travels \(50 \mathrm{~km}\) in one hour. Its average speed is \(50 \mathrm{~km}\) per hour \((50 \mathrm{~km} / \mathrm{h})\)
\(
\text { Speed }=\frac{\text { Distance }}{\text { Time }}=\frac{50 \mathrm{~km}}{1 \text { hour }}
\)

Example 9: During a journey, a train moves at a speed of 50 kilometers per hour for the first 2 hours and 70 kilometers per hour for the next 3 hours. Find the average speed of the train using the average speed formula.

Answer: We know that total distance \(=s_1 \)+\(s_2\)
We know that total time \(=t_1\)+\(t_2\)
Average Speed Formula = Total Distance/Total Time
Average Speed Formula \(=\frac{s_1 \times t_1+s_2 \times t_2}{t_1+t_2}=(50 \times 2+70 \times 3) \div(2+3)\)
\(=(310) \div(5)=62 \text { kilometer/hour }\)
Therefore, the average speed of the train is \(62 \mathrm{kmph}\).

Average speed of particles in different cases
Case I: If an object travels distance \(s_1, s_2, s_3\), .., etc., with speeds \(v_1, v_2, v_3, \ldots\), etc. , in same direction, then the distance travelled \(=s_1+s_2+s_3+\ldots\)
Total time taken \(=\frac{s_1}{v_1}+\frac{s_2}{v_2}+\frac{s_3}{v_3}+\ldots\)
Average speed, \(v_{\mathrm{av}}=\frac{s_1+s_2+\ldots}{\left(\frac{s_1}{v_1}+\frac{s_2}{v_2}+\ldots\right)}\)
If \(s_1=s_2=s\), i.e. the body covers equal distances with different speeds, then
\(
\begin{array}{l}
v_{\mathrm{av}}=\frac{2 s}{s\left(\frac{1}{v_1}+\frac{1}{v_2}\right)} \\
v_{\mathrm{av}}=\frac{2 v_1 v_2}{v_1+v_2}
\end{array}
\)

Example 10: A car covers the first half of the distance between two places at a speed of \(40 \mathrm{kmh}^{-1}\) and second half at \(60 \mathrm{kmh}^{-1}\). Calculate the average speed of the car.

Answer: Given, speed in first half, \(v_1=40 \mathrm{kmh}^{-1}\)
Speed in second half, \(v_2=60 \mathrm{kmh}^{-1}\)
\(\because\) Car covers equal distance with different speeds.
\(\therefore\) Average speed of car,
\(
\begin{aligned}
v_{\mathrm{av}} & =\frac{2 v_1 v_2}{v_1+v_2} \\
\Rightarrow \quad v_{\mathrm{av}} & =\frac{2(40)(60)}{40+60}=48 \mathrm{kmh}^{-1}
\end{aligned}
\)

Case II: If an object travels with speeds \(v_1, v_2, v_3, \ldots\), etc., during time intervals \(t_1, t_2, t_3, \ldots\), etc., then total distance travelled, \(s=v_1 t_1+v_2 t_2+v_3 t_3+\ldots\)
Total time taken \(=t_1+t_2+t_3+\ldots\)
So, average speed, \(v_{\mathrm{av}}=\frac{v_1 t_1+v_2 t_2+v_3 t_3+\ldots}{t_1+t_2+t_3+\ldots}\)

Case III: If \(t_1=t_2=t_3=\ldots=t_n=t\), then we have
\(
\begin{array}{l}
v_{\mathrm{av}}=\frac{\left(v_1+v_2+\ldots+v_n\right) t}{n t} \\
v_{\mathrm{av}}=\frac{v_1+v_2+\ldots+v_n}{n}
\end{array}
\)

Example 11: Ashok while driving to school, computes the average speed for his trip to be \(20 \mathrm{~kmh}^{-1}\). On his return trip along the same route, there is less traffic and the average speed is \(40 \mathrm{~kmh}^{-1}\). What is the average speed for Ashok’s trip?

Answer: Let \(t_1\) and \(t_2\) be the time taken by Ashok to go to school and come back from the school, respectively. Let \(s\) be its distance covered in one way, then
\(
t_1=\frac{s}{20} \mathrm{~h} \text { and } t_2=\frac{s}{40} \mathrm{~h}
\)

Total time taken \(=t_1+t_2=\frac{s}{20}+\frac{s}{40}=\frac{3 s}{40} \mathrm{~h}\)
Total distance covered \(=2 \mathrm{~s}\)
\(\therefore\) Average speed \(=\frac{2 s}{3 s} \times 40=\frac{80}{3}=26.67 \mathrm{~kmh}^{-1}\)

Example 12: A particle travelled half the distance with a speed \(v_0\). The remaining part of the distance was covered with speed \(v_1\) for half the time and with speed \(v_2\) for the other half of the time. Find the average speed of the particle.

Answer:  If \(s\) is the total distance travelled by the particle, then
\(
\frac{s}{2}=v_0 t_1 \Rightarrow t_1=\frac{s}{2 v_0}
\)
If \(t_2\) is the time taken by particle to travel remaining distance \(s / 2\), then \(\frac{s}{2}=\frac{v_1 t_2}{2}+\frac{v_2 t_2}{2}=\left(v_1+v_2\right) \frac{t_2}{2}\) or \(t_2=\frac{s}{\left(v_1+v_2\right)}\)

Average speed \(=\frac{s}{t_1+t_2}=\frac{s}{\frac{s}{2 v_0}+\frac{s}{\left(v_1+v_2\right)}}=\frac{2 v_0\left(v_1+v_2\right)}{v_1+v_2+2 v_0}\)

Instantaneous speed

The speed of a particle at any instant of time is known as its instantaneous speed.
\(
\text { Instantaneous speed }=\lim _{\Delta t \rightarrow 0} \frac{\Delta s}{\Delta t}=\frac{d s}{d t}
\)
where, \(s\) represents distance.

Example 13: A particle experiences the displacement given by the function \(s(t)=10\) \(\mathrm{t}^2-5 \mathrm{t}+1\). Compute its instantaneous speed at time \(\mathrm{t}=3 \mathrm{~s}\).

Answer: The instantaneous speed is given by = \(\frac{d s}{d t}=\frac{d (10 t^2-5 t+1)}{d t}=(20 t-5)\)
At \(t=3 s\), Instantaneous Speed = \((20(3)-5)=55 \mathrm{~m} / \mathrm{s}\)

Average vs Instantaneous Speed

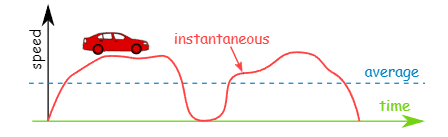
Average Speed (Blue dotted line): how far something travels over a period of time. But speed can change as time goes by. A car can go faster and slower, maybe even stop at lights (as shown in above figure).

Instantaneous Speed (red curve): the speed at an instant in time. We can try to measure it by using a very short span of time (the shorter the better).

Velocity

The rate of change of position or displacement of an object with time is called the velocity of that object.
i.e. \(\quad\) Velocity \(=\frac{\text { Displacement }}{\text { Time }}\)

It is a vector quantity. The unit of velocity in SI or MKS system is \(\mathrm{ms}^{-1}\) and in CGS system is \(\mathrm{cms}^{-1}\). Its dimensional formula is \(\left[\mathrm{M}^0 \mathrm{LT}^{-1}\right]\). In 1-D motion, the velocity of an object is taken to be positive, if the object is moving towards the right of the origin and is taken to be negative, if the object is moving towards the left of the origin.

Average velocity

The ratio of the total displacement to the total time taken is called average velocity.
\(
\text { Average velocity }=v_{avg}=\frac{\text { Total displacement }(\Delta x)}{\text { Total time }(\Delta t)}
\)

If velocity of the object changes at a uniform rate, then
\(
v_{avg}=\frac{\text { Initial velocity }+ \text { Final velocity }}{2}
\)

Note: for a given time interval, average velocity has single value while average speed can have many values depending on path followed.

Instantaneous velocity

The velocity of a particle at any instant of time is known as its instantaneous velocity.
\(
v=\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=\frac{d x}{d t}
\)

Note: The magnitude of average velocity may be less than or equal to the average speed for a particular motion. But the magnitude of instantaneous velocity is always equal to the instantaneous speed for a particular instant.

Velocity vector in 3-d cartesian co-ordinates is shown below:

\(
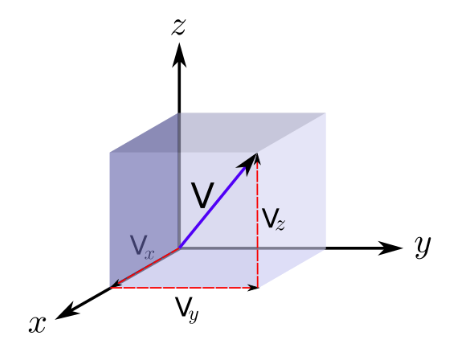
\vec{v}=\frac{d \vec{r}}{d t}=\frac{d}{d t}(x \hat{i}+y \hat{j}+z \hat{k})=\frac{d x}{d t} \hat{i}+\frac{d y}{d t} \hat{j}+\frac{d z}{d t} \hat{k}=v_x \hat{i}+v_y \hat{j}+v_z \hat{k}
\)

Uniform Motion 

Uniform Motion is a type of motion in which an object travels at a uniform speed.

• It is defined as the motion of an object traveling in a straight line.
• The velocity of the object remains constant along the straight line as it covers equal distances in equal intervals of time.
• The magnitude of displacement is equal to the actual distance covered by the body in uniform motion.
• The slope of the distance-time graph of uniform motion gives the velocity of the body.
  
  

For example, If the car below has uniform motion and it covers 10km in equal time interval (0-1 and 1-2, 2-3 and 3-4 time interval car speed is same 10km) as shown below. In this case the displacement vs time graph will be linear and is a straight line.

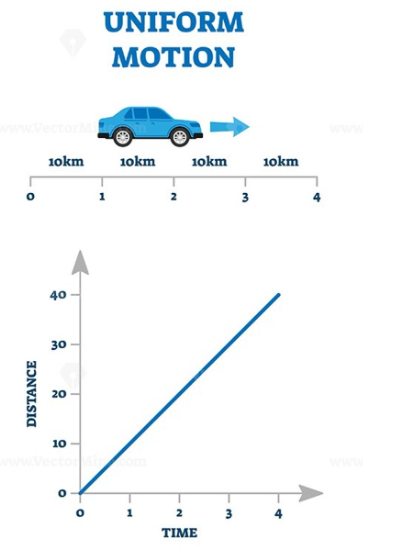
From the graph, we can see that the slope is constant. Therefore,
\(
\text { Velocity }=\frac{\text { Change in displacement }}{\text { Change in time }}=\text { Constant }
\)

Mathematically we can write \(s(t)=10t\). Therefore velocity \(v=\frac{d s(t)}{d t}=10=\text { Constant }\)

Note: For uniform motion Average speed \(=\mid\) average velocity \(|=|\) instantaneous velocity \(\mid\)

Non-uniform Motion

As the name suggests that a motion in which the body covers unequal distances in equal intervals of time is known as a non-uniform motion. You can see from the waveform below between time interval 0-1, car speed is 20km, 1-2 it is 5km that is car covers unequal distances in equal time intervals. Therefore, the displacement time graph will not be linear.

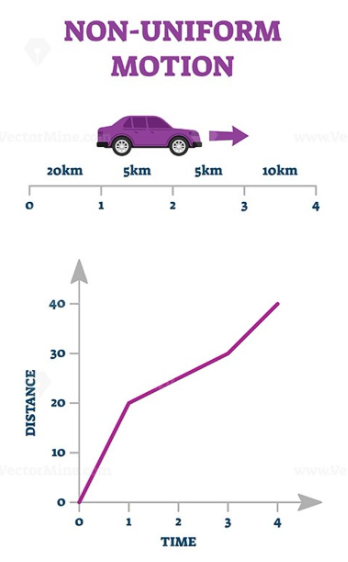
Uniform and non-uniform velocity

An object is said to have uniform velocity, if the magnitude and direction of its velocity remains constant. This is only possible when the object moves along a straight line without reversing its direction. However, an object is said to have non-uniform velocity, if either magnitude or direction of velocity change with respect to time.

Velocity versus Speed

• Velocity of an object can be changed by changing the object’s speed or direction of motion or both.
• For an object in a time interval \((t)\); \(\mid\) Velocity \(\mid \leq\) Speed i.e. The magnitude of velocity of an object is always equal to or less than its speed.
• If a body is moving in a straight line, then the magnitude of its speed and velocity will be equal.
• Average velocity could be zero or positive or negative but average speed is always positive for a moving body.

Example 14: In one second, a particle goes from point \(A\) to point \(B\) moving in a semicircular path as shown in figure. Find the magnitude of average velocity.

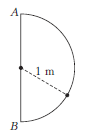
Answer: Given, \(t=1 \mathrm{~s}\) and radius, \(R=1.0 \mathrm{~m}\)
The shortest distance between the final position \((B)\) and initial position \(A\) is \(A B\), which is the displacement of the particle.
\(\therefore\) Total displacement \((A B)=2 R=2 \times 1.0=2 \mathrm{~m}\)
Thus, average velocity, \(v_{a v}=\frac{\text { Total displacement }}{\text { Total time taken }}\)
\(
=\frac{A B}{\Delta t}=\frac{2.0}{1.0} \mathrm{~ms}^{-1}=2 \mathrm{~ms}^{-1}
\)

Example 15: A farmer has to go \(500 \mathrm{~m}\) due north, \(400 \mathrm{~m}\) due east and \(200 \mathrm{~m}\) due south to reach his field. If he takes 20 min to reach the field,
(i) what distance he has to walk to reach the field?
(ii) what is the displacement from his house to the field?
(iii) what is the average speed of farmer during the walk?
(iv) what is the average velocity of farmer during the walk?

Answer: 

(i) Distance \(=A B+B C+C D =(500+400+200)=1100 \mathrm{~m}\)
(ii) Displacement \(=A D=\sqrt{(A B-C D)^2+B C^2} =\sqrt{(500-200)^2+(400)^2}=500 \mathrm{~m}\)
(iii) Average speed \(=\frac{\text { Total distance }}{\text { Total time }}=\frac{1100}{20}=55 \mathrm{~m} / \mathrm{min}\)
(iv) Average velocity \(=\frac{A D}{t}=\frac{500}{20}=25 \mathrm{~m} / \mathrm{min}(\) along \(A D)\)

Example 16: Joseph jogs from one end \(A\) to the other end \(B\) of a straight \(300 \mathrm{~m}\) road in \(2 \mathrm{~min} ~50 \mathrm{~s}\) and then turns around and jogs \(100 \mathrm{~m}\) back to point \(C\) in another 1 min. What are Joseph’s average speeds and velocities in jogging (i) from \(A\) to \(B\) and (ii) from \(A\) to \(C\) ?

Answer: Given, distance covered from \(A\) to \(B=300 \mathrm{~m}\)
\(
\text { Time }=2 \min 50 \mathrm{~s}=(2 \times 60)+50 \mathrm{~s}=170 \mathrm{~s}
\)

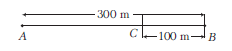
(i)
\(
\begin{aligned}
\text { Average speed } & =\frac{\text { Distance covered }}{\text { Time }} \\
& =\frac{300}{170}=1.76 \mathrm{~ms}^{-1} \\
\text { Average velocity } & =\frac{\text { Displacement along } A B}{\text { Time }} \\
& =\frac{300}{170}=1.76 \mathrm{~ms}^{-1} \text { along } A B
\end{aligned}
\)
(ii) When Joseph turns around from \(B\) to \(C\) towards \(A\), then
\(
\begin{aligned}
\text { Average speed } & =\frac{\text { Distance covered }}{\text { Time }}=\frac{400}{230}=1.74 \mathrm{~ms}^{-1} \\
\text { Average velocity } & =\frac{\text { Displacement } A C}{\text { Time }}=\frac{200}{230} \text { along } A C \\
& =0.87 \mathrm{~ms}^{-1} \text { along } A C
\end{aligned}
\)

Example 17: The position of an object moving along \(X\)-axis is given by \(x=3 t-4 t^2+t^3\), where \(x\) is in metres and \(t\) in seconds. Find the position of the object at the following values of :
(i) \(2 s\),
(ii) \(4 s\),
(iii) What is the object’s displacement between \(t=0 \mathrm{~s}\) and \(t=4 \mathrm{~s}\) ?; and
(iv) What is its average velocity for the time interval from \(t=2\) s to \(t=4 \mathrm{~s}\) ?

Answer: Using \(x=3 t-4 t^2+t^3 \dots(i)\) with SI units
(i) Substituting \(t=2 \mathrm{~s}\) in Eq. (i), we get
\(
x_2=3(2)-4(2)^2+(2)^3=-2 \mathrm{~m}
\)

Thus, the position of the object at \(t=2 \mathrm{~s}\) is \(x_2=-2 \mathrm{~m}\).
(ii) Substituting \(t=4 \mathrm{~s}\) in \(\mathrm{Eq}\). (i), we get
\(
x_4=3(4)-4(4)^2+(4)^3=12-64+64=12 \mathrm{~m}
\)

Thus, the position of the object at \(t=4 \mathrm{~s}\) is \(x_4=12 \mathrm{~m}\).
(iii) The displacement of the object between \(t=0 \mathrm{~s}\) and \(t=4 \mathrm{~s}\) can be calculated as follows :
The position of the object at \(t=0 \mathrm{~s}\) is \(x=0\).
\(
\begin{aligned}
\Delta x & =\text { Final position }- \text { Initial position }=x_4-x_0 \\
& =12 \mathrm{~m}-0 \mathrm{~m}=12 \mathrm{~m}
\end{aligned}
\)

Hence, the displacement between \(t=0 \mathrm{~s}\) and \(t=4 \mathrm{~s}\) is \(12 \mathrm{~m}\).
(iv) The displacement of the object from \(t=2 \mathrm{~s}\) to \(t=4 \mathrm{~s}\) is
\(
\Delta x=x_4-x_2=12 \mathrm{~m}-(-2 \mathrm{~m})=14 \mathrm{~m}
\)

The time interval from \(t=2 \mathrm{~s}\) to \(t=4 \mathrm{~s}\) is
\(
\Delta t=4 \mathrm{~s}-2 \mathrm{~s}=2 \mathrm{~s}
\)

The average velocity of the object from \(t=2 \mathrm{~s}\) to \(t=4 \mathrm{~s}\) is given by the relation
\(
\begin{aligned}
v_{\mathrm{av}} & =\frac{\Delta x}{\Delta t}=\frac{14 \mathrm{~m}}{2 \mathrm{~s}} \\
& =7 \mathrm{~ms}^{-1}
\end{aligned}
\)

Acceleration

The time rate of change of velocity of a body is called acceleration.
\(
\therefore \quad \text { Acceleration }=\frac{\text { Change in velocity }(\Delta v)}{\text { Time interval }(\Delta t)}
\)

If in a given time interval, the velocity of a body changes from \(u\) to \(v\), then acceleration \(a\) is expressed as
\(
a=\frac{\text { Final velocity }- \text { Initial velocity }}{\text { Time interval }}=\frac{v-u}{t}
\)
It is a vector quantity. Its SI unit is \(\mathrm{ms}^{-2}\) and CGS unit is \(\mathrm{cms}^{-2}\).
Its dimensional formula is \(\left[\mathrm{M}^0 \mathrm{LT}^{-2}\right]\). Its direction is same as that of change in velocity (not of the velocity).
There are three possible ways by which change in velocity may occur

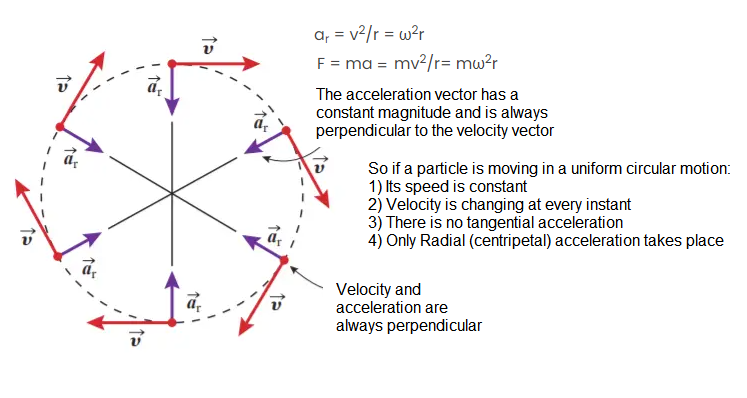
Case 1: When only direction of velocity changes, then acceleration is perpendicular to velocity. e.g. Uniform circular motion. The movement of a body following a circular path is called a circular motion. Now, the motion of a body moving with constant speed along a circular path is called Uniform Circular Motion. Here, the speed is constant but the velocity changes. If a particle is moving in a circle, it must have some acceleration acting towards the centre which is making it move around the centre. Since this acceleration is perpendicular to the velocity of a particle at every instant, it is only changing the direction of velocity and not magnitude and that’s why the motion is uniform circular motion. We call this acceleration centripetal acceleration (or radial acceleration), and the force acting towards the centre is called centripetal force.

Case 2: When only magnitude of velocity changes, then acceleration is parallel or anti-parallel to velocity. e.g. Motion under gravity.

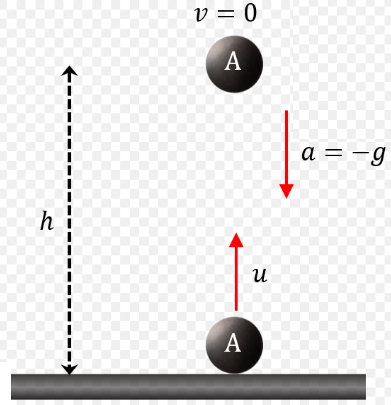
If a body is projected vertically upward
Equation of motion: Taking initial position as origin and direction of motion (i.e., vertically up) as positive
\(\mathrm{a}=-g\) [As acceleration is downwards while motion upwards]
So, if the body is projected with velocity \(u\) and after time \(t\) it reaches up to height \(h\) then
\(
v=u-g t
\)
\(
h=u t-\frac{1}{2} g t^2
\)
\(
v^2=u^2-2 g h
\)

For maximum height \(\mathrm{v}=0\)
So from above equation
\(
\begin{array}{l}
{u}=g t \\
h=\frac{1}{2} g t^2 \\
\text { and } u^2=2 g h
\end{array}
\)

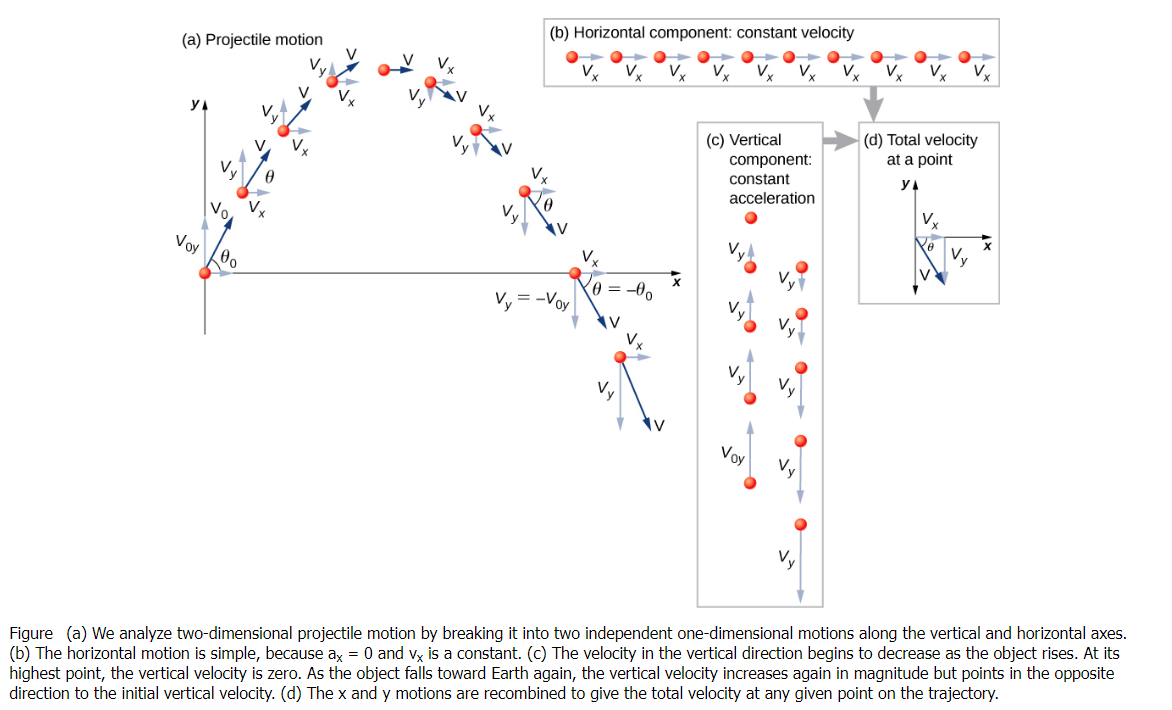
Case 3: When both magnitude and direction of velocity changes, then acceleration has two components : one is perpendicular to velocity and another is parallel or anti-parallel to velocity. e.g. Projectile motion.

A particle thrown in the space which moves under the effect of gravity only is called a projectile.

• Projectile motion is the combination of two motions.
• Projectile Motion = Horizontal Motion + Vertical Motion

Retardation

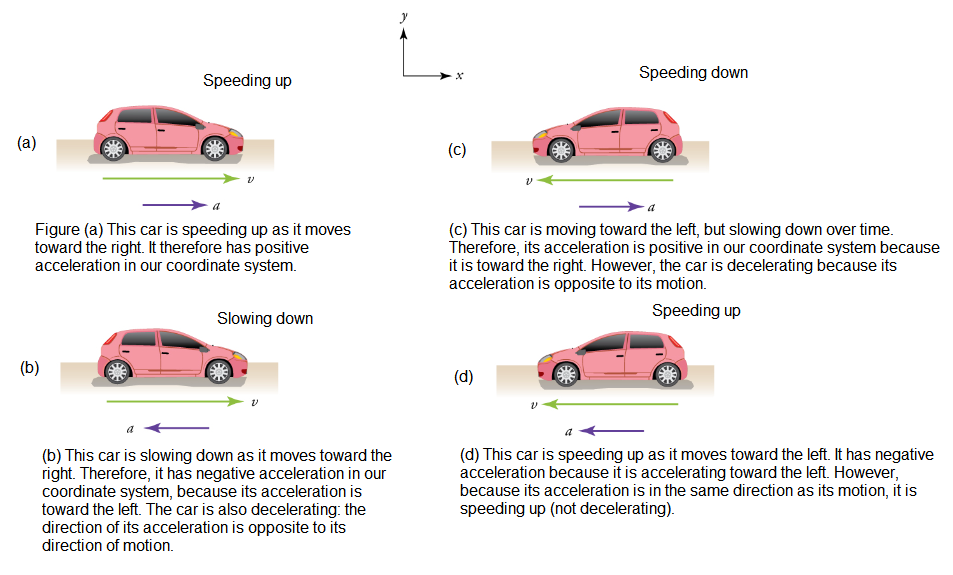
When the velocity of a body increases with time, acceleration is positive and when the velocity of a body decreases with time (i.e. \(u>v\) ), then acceleration becomes negative. This negative acceleration is also called deceleration or retardation. In other words, retardation opposes the motion of body.

Deceleration always refers to acceleration in the direction opposite to the direction of the velocity. Deceleration always reduces speed. Negative acceleration, however, is acceleration in the negative direction in the chosen coordinate system. Negative acceleration may or may not be deceleration, and deceleration may or may not be considered negative acceleration. For example, consider Figure below.

Average acceleration

When an object is moving with a variable acceleration, then the average acceleration of the object for the given motion is defined as the ratio of the total change in velocity of the object to the total time taken.
\(
\text { Average acceleration }=\frac{\text { Total change in velocity }}{\text { Total time taken }}
\)

Note: The average acceleration can be positive or negative depending upon the sign of change of velocity. It is zero, if the change in velocity of the object in the given interval of time is zero.

Instantaneous acceleration

The acceleration of an object at a given instant of time or at a given point during the motion, is called its instantaneous acceleration. i.e.
\(
\vec{a}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \vec{v}}{\Delta t}=\frac{d \vec{v}}{d t}=\frac{d^2 \vec{s}}{d t^2}
\)

Acceleration vector in 3-d cartesian co-ordinates is shown below:

\(
\vec{a}=\frac{d \vec{v}}{d t}=\frac{d}{d t}\left(v_x \hat{i}+v_y \hat{j}+v_z \hat{k}\right)=\frac{d v_x}{d t} \hat{i}+\frac{d v_y}{d t} \hat{j}+\frac{d v_z}{d t} \hat{k}=a_x \hat{i}+a_y \hat{j}+a_z \hat{k}
\)

Key points regarding acceleration

Following are the important points for motion of an object having some acceleration

• A body falling down from a height or a body rolling down on a smooth inclined plane has uniform acceleration.
• If a car travelling along a straight road, increases its speed by unequal amounts in equal intervals of time, then the car is said to be moving with non-uniform acceleration.
• The acceleration is created by accelerator of the vehicles and the applications of breaks give the uniform deceleration to the vehicles. However, the acceleration produced in spring block system is non-uniform acceleration.
• If a particle is accelerated for time \(t_1\) with acceleration \(a_1\) and for time \(t_2\) with acceleration \(a_2\), then average acceleration is
  \(
  a_{\mathrm{av}}=\frac{a_1 t_1+a_2 t_2}{t_1+t_2}
  \)
• Acceleration can also be written as
  \(
  a=\frac{d v}{d t}=\frac{d v}{d x} \cdot \frac{d x}{d t}=v\left(\frac{d v}{d x}\right)
  \)

Example 18: A car starts from rest, attains a velocity of \(18 \mathrm{~kmh}^{-1}\) with an acceleration of \(0.5 \mathrm{~ms}^{-2}\), travels \(4 \mathrm{~km}\) with this uniform velocity and then comes to halt with a uniform deceleration of \(0.4 \mathrm{~ms}^{-2}\). Calculate the total time of travel of the car.

Answer:Let the car be accelerated from \(A\) to \(B\), it moves with uniform velocity from \(B\) to \(C\) of \(4 \mathrm{~km}\) distance and then moves with uniform deceleration of \(0.4 \mathrm{~ms}^{-2}\) from \(C\) to \(D\) as shown below.

For motion of car from \(A\) to \(B, a=0.5 \mathrm{~ms}^{-2}\)
\(
\begin{aligned}
u & =0 \text { and } v=18 \mathrm{~km} \mathrm{~h}^{-1} \\
& =18 \times \frac{5}{18} \mathrm{~ms}^{-1}=5 \mathrm{~ms}^{-1}
\end{aligned}
\)
\(
\text { Time, } \quad t_1=\frac{v-u}{a} \dots(i)
\)
Substituting given values of \(v, u\) and \(a\) for \(A\) to \(B\) motion, we get
\(
t_1=\frac{5-0}{0.5}=10 \mathrm{~s} \dots(ii)
\)
For motion of car from \(B\) to \(C\), and
\(
\begin{aligned}
s & =4 \mathrm{~km}=4000 \mathrm{~m} \\
v & =5 \mathrm{~ms}^{-1} \\
t_2 & =\frac{\text { distance }}{\text { velocity }} \\
& =\frac{4000}{5}=800 \mathrm{~s} \dots(iii)
\end{aligned}
\)
For motion of car from \(C\) to \(D, v=0, u=5 \mathrm{~ms}^{-1}\) and \(a=-0.4 \mathrm{~ms}^{-2}\) (negative sign shows deceleration)
Time taken, \(t_3=\frac{v-u}{a}=\frac{0-5}{-0.4}\)
\(
=\frac{-5}{-0.4}=12.5 \mathrm{~s} \dots(iv)
\)
Total time taken, \(T=t_1+t_2+t_3\)
Substituting values of \(t_1, t_2\) and \(t_3\) from Eqs. (ii), (iii) and (iv) respectively, we get
\(
T=(10+800+12.5) \mathrm{s}=822.5
\)
Thus, total time of travel of the car is \(822.5 \mathrm{~s}\).

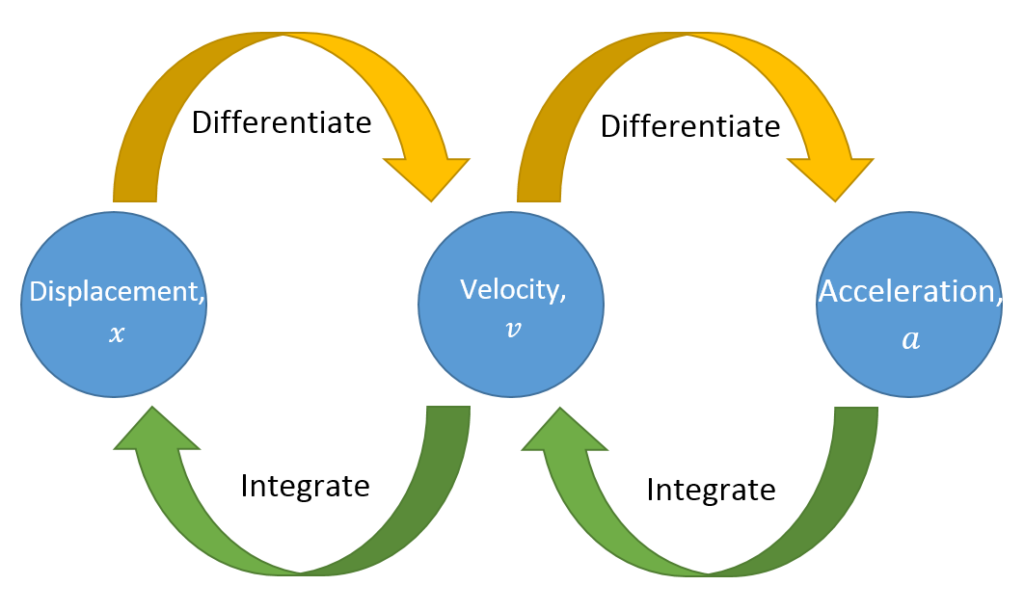
Relation Among Displacement, Velocity and Acceleration

• Instantaneous velocity is the slope of displacement time curve: \(v=\frac{d x}{d t} \text { or } x=\int v d t\)
• Velocity-time curve area gives displacement: \(x=\int v d t\)
• Slope of velocity-time curve = instantaneous acceleration: \(a=\frac{d v}{d t} \text { or } v=\int a d t\)
• Acceleration-time curve area gives velocity: \(v=\int a d t\)

 

Important Points about 1-D Motion:

• Distance \(\geq\) I displacement I and Average speed \(\geq\) | average velocity |
• If distance > | displacement | this implies
  (a) at least at one point in path, velocity is zero.
  (b) The body must have retarded during the motion.
• Speed increase if acceleration and velocity both are positive or negative (i.e. both have same sign).
• In 1-D motion \(a=\frac{d v}{d t}=\frac{d v}{d x} \times \frac{d x}{d t} =v \frac{d v}{d x}\)

Graphical representation of Motion 

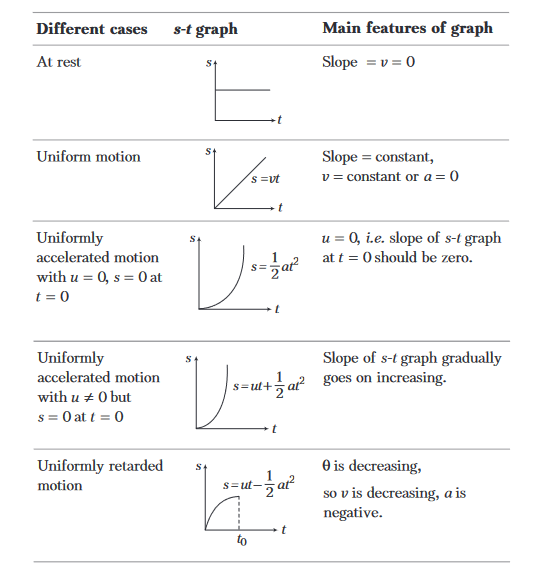
Displacement-time graph

• Displacement-time graph gives instantaneous value of displacement at any instant.
• The slope of tangent drawn to the graph at any instant of time gives the instantaneous velocity at that instant.
• The \(s-t\) graph cannot make sharp turns.

Different cases of displacement-time graph

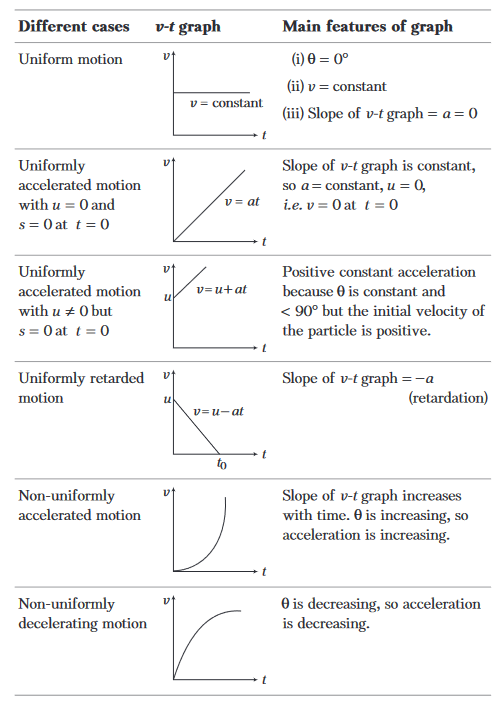
Velocity-time graph

• Velocity-time graph gives the instantaneous value of velocity at any instant.
• The slope of tangent drawn on graph gives instantaneous acceleration.
• Area under \(v-t\) graph with time axis gives the value of displacement covered in given time.
• The \(v\) – \(t\) curve cannot take sharp turns.

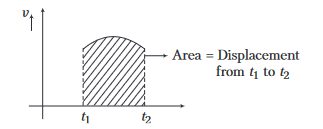
If \(\mathrm{v}=\mathrm{f}(\mathrm{t})\)
\(
\mathrm{v}=\frac{\mathrm{dx}}{\mathrm{dt}} \Rightarrow \int_{\mathrm{x}_1}^{\mathrm{x}_2} \mathrm{dx}=\int_{\mathrm{t}_1}^{\mathrm{t}_2} \mathrm{vdt} \Rightarrow \mathrm{x}_2-\mathrm{x}_1=\int_{\mathrm{t}_1}^{\mathrm{t}_2} \mathrm{vdt}
\)
\(\Rightarrow\) Change in position \(=\) displacement
\(=\) area between velocity curve and time axis, from \(t_1 \text { to } t_2 \text {. }\)

Different cases of velocity-time graph

Acceleration-time graph

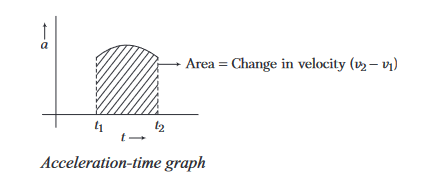
The area of the \(a\) – \(t\) graph between time \(t_1\) to \(t_2\) gives the change in velocity.
\(
\begin{aligned}
a & =\frac{d v}{d t} \\
\Rightarrow \quad d v & =a d t \\
\Rightarrow \quad \int_{v_1}^{v_2} d v & =\int_{t_1}^{t_2} a d t \\
v_2-v_1 & =\int_{t_1}^{t_2} a d t
\end{aligned}
\)
Change in velocity \(=\) Area of the \(a-t\) graph

Kinematic Equations for Uniformly Accelerated Motion

When a body is moving along a straight line with uniform acceleration, then its motion is called uniformly accelerated motion. For this motion, we can establish the relation between velocity, acceleration and the distance travelled by the body in a particular time interval by a set of equations. These equations are known as kinematic equations or equations of motion.

The three equations of motion on a straight line are

• \(v=u+a t\)
• \(s=u t+\frac{1}{2} a t^2\)
• \(v^2-u^2=2 a s\)

where, \(u\) is the initial velocity of the body, \(a\) is the uniform acceleration of the body, \(v\) is the final velocity of the body after \(t\) second and \(s\) is the distance travelled in this time.

• Distance travelled by a body in \(n\)th second,
  \(
  s_n=u+\frac{1}{2} a(2 n-1)
  \)

Note:

• If initial position of a particle is \(\mathrm{r}_0\), then position at time \(t\) can be written as
  \(
  r=r_0+s=r_0+u t+\frac{1}{2} a t^2
  \)
• Stopping distance When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety. \(
  v^2=u^2+2 a s \ldots \ldots \text { (i) }
  \)
  In the case of stopping distance, the final velocity is zero, and acceleration must be negative (Friction force will oppose the motion), or the body must be under retardation motion.
  Let the retarding force (Friction, air drag, etc.) be \(F\) acting on the body of mass \(m\),
  Then the acceleration of the vehicle, \(a=\frac{-F}{m}\).
  Now put the value of final velocity \((v=0)\) and acceleration in equation (i).
  \(
  \begin{array}{l}
  0^2=u^2+2 a s \\
  \Rightarrow s=-\frac{u^2}{2 a}=\frac{m u^2}{2 F}
  \end{array}
  \)
  Thus the stopping distance formula for any retarding force \(F\) will be,
  \(
  s=\frac{m u^2}{2 F} \text {. }
  \)

Example 19: A particle is moving along the \(X\)-axis and its position-time graph is shown. Determine the sign of acceleration.

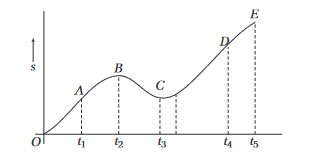
Answer: By observing the s-t graph, we can determine the sign of acceleration. Recall, if the graph is concave upwards, the slope is increasing; if it is concave downward, the slope is decreasing; and if the graph is straight line, the slope is constant.

\(O A\) : Slope is increasing, \(v\) is increasing and \(a\) is positive.
\(A B\) : Slope is constant, \(v\) is constant and \(a=0\).
\(B C\) : Slope is decreasing, \(v\) is decreasing and \(a\) is negative.
\(C D\) : Slope is increasing, \(v\) is increasing and \(a\) is positive.
\(D E\) : Slope is constant, \(v\) is constant and \(a=0\).

Example 20: With the help of the given velocity-time graph, find the (i) displacement in first three seconds and (ii) acceleration

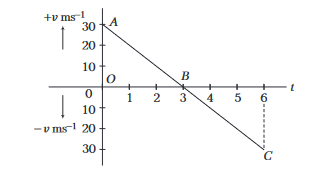
Answer: (i) Displacement in first three seconds \(=\) Area of triangle \(O A B\)
\(
=\frac{1}{2}(O B) \times(O A)=\frac{1}{2}(3) \times(30)=+45 \mathrm{~m}
\)
(ii) Acceleration \(=\) Slope of \(v-t\) graph
As, \(v\) – \(t\) graph is a straight line. So, consider the slope of line \(A B\).
\(\therefore\) Slope of line \(A B=\frac{y_2-y_1}{x_2-x_1}=\frac{0-30}{3}=-10 \mathrm{~ms}^{-2}\)
So, the acceleration is negative.

Example 21: A car accelerates from rest at a constant rate \(\alpha\) for some time, after which it decelerates at a constant rate \(\beta\) to come to rest. If the total time elapsed is \(t\) second evaluate (i) the maximum velocity reached and (ii) the total distance travelled.

Answer: (i) Let the car accelerates for time \(t_1\) and decelerates for time \(t_2\). Then, \(t=t_1+t_2 \dots(i)\)
and corresponding velocity-time graph will be as shown in figure.

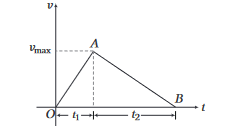
From the graph,
\(
\alpha=\text { slope of line } O A=\frac{v_{\max }}{t_1}
\)
or \(\quad t_1=\frac{v_{\max }}{\alpha} \dots(ii)\)
and \(\quad \beta=-\) slope of line \(A B=\frac{v_{\max }}{t_2}\)
or \(\quad t_2=\frac{v_{\max }}{\beta} \dots(iii)\)
From Eqs. (i), (ii) and (iii), we get
\(
\frac{v_{\max }}{\alpha}+\frac{v_{\max }}{\beta}=t
\)
or \(\quad v_{\max }\left(\frac{\alpha+\beta}{\alpha \beta}\right)=t\) or \(v_{\max }=\frac{\alpha \beta t}{\alpha+\beta}\)
\(
\begin{aligned}
\text { (ii) Total distance } & =\text { Displacement }=\text { Area under } v-t \text { graph } \\
& =\frac{1}{2} \times t \times v_{\max } \\
& =\frac{1}{2} \times t \times \frac{\alpha \beta t}{\alpha+\beta} \\
\text { or Distance } & =\frac{1}{2}\left(\frac{\alpha \beta t^2}{\alpha+\beta}\right)
\end{aligned}
\)

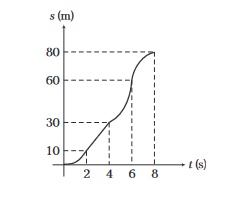
Example 22: Velocity-time graph of a particle moving in a straight line is shown in figure.

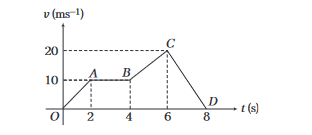
Plot the corresponding displacement-time graph of the particle, if at time \(t=0\), displacement \(s=0\).

Answer:Displacement \(=\) Area under velocity-time graph
Hence, \(\quad s_{O A}=\frac{1}{2} \times 2 \times 10=10 \mathrm{~m}\)
\(
s_{A B}=2 \times 10=20 \mathrm{~m}
\)
\(
s_{O A B}=10+20=30 \mathrm{~m}
\)
\(
s_{B C}=\frac{1}{2} \times 2(10+20)=30 \mathrm{~m}
\)
\(
s_{O A B C}=30+30=60 \mathrm{~m}
\)
and
\(
s_{C D}=\frac{1}{2} \times 2 \times 20=20 \mathrm{~m}
\)
\(
s_{\text {OABCD }}=60+20=80 \mathrm{~m}
\)

Between \(0 \mathrm{~s}\) to \(2 \mathrm{~s}\) and \(4 \mathrm{~s}\) to \(6 \mathrm{~s}\), motion is accelerated, hence displacement-time graph is a parabola. Between \(2 \mathrm{~s}\) to \(4 \mathrm{~s}\), motion is uniform, so displacement-time graph will be a straight line. Between \(6 \mathrm{~s}\) to \(8 \mathrm{~s}\), motion is decelerated, hence displacement-time graph is again a parabola but inverted in shape.
At the end of \(8 \mathrm{~s}\) velocity is zero, therefore slope of displacement-time graph should be zero. The corresponding graph is shown in figure.

Example 23: A rocket is fired vertically upwards with a net acceleration of \(4 \mathrm{~ms}^{-2}\) and initial velocity zero. After \(5 \mathrm{~s}\), its fuel is finished and it decelerates with \(\mathrm{g}\). At the highest point, its velocity becomes zero. Then, it accelerates downwards with acceleration \(g\) and return back to ground. Plot velocity-time and displacement-time graphs for the complete journey. (Take, \(g=10 \mathrm{~ms}^{-2}\) )

Answer: In the graphs, \(v_A=a t_{O A}=(4)(5)=20 \mathrm{~ms}^{-1}\)
\(
\begin{aligned}
& v_B =0=v_A-g t_{A B} \\
\Rightarrow & t_{A B} =\frac{v_A}{g}=\frac{20}{10}=2 \mathrm{~s} \\
\therefore & t_{O A B} =(5+2) \mathrm{s}=7 \mathrm{~s}
\end{aligned}
\)

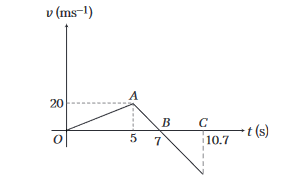
Now, \(s_{O A B}=\) area under \(v-t\) graph between 0 to \(7 \mathrm{~s}\)
\(
=\frac{1}{2}(7)(20)=70 \mathrm{~m}
\)

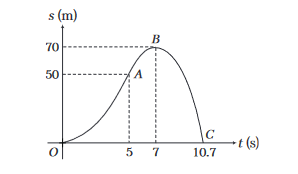
Now,
\(
\begin{array}{l}
\left|s_{O A B}\right|=\left|s_{B C}\right|=\frac{1}{2} g t_{B C}^2 \\
\therefore \quad 70=\frac{1}{2}(10) t_{B C}^2 \\
\Rightarrow \quad t_{B C}=\sqrt{14}=3.7 \mathrm{~s} \\
\therefore \quad t_{O A B C}=7+3.7=10.7 \mathrm{~s} \\
\end{array}
\)
Also, \(s_{O A}=\) area under \(v\) – \(t\) graph between \(O A\)
\(
=\frac{1}{2}(5)(20)=50 \mathrm{~m}
\)

Example 24: Acceleration-time graph of a particle moving in a straight line is shown in figure. Velocity of particle at time \(t=0\) is \(2 \mathrm{~ms}^{-1}\). Find velocity at the end of fourth second.

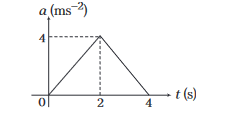
Answer: According to acceleration time-graph, \(d v=a d t\) or change in velocity \(=\) area under \(a\) – \(t\) graph Hence,
\(
\begin{array}{rlrl}
& \text { Hence, } & v_f-v_i & =\frac{1}{2}(4)(4)=8 \mathrm{~ms}^{-1} \\
\therefore & v_f & =v_i+8=(2+8) \mathrm{ms}^{-1}=10 \mathrm{~ms}^{-1}
\end{array}
\)

Example 25: The acceleration versus time graph of a particle moving along a straight line is shown in the figure. Draw the respective velocity-time graph.

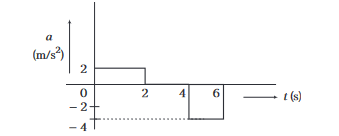
Assume at \(t=0, v=0\).

Answer: From \(t=0\) to \(t=2 \mathrm{~s}, a=+2 \mathrm{~m} / \mathrm{s}^2 \Rightarrow v=a t=2 t\)
or \(v\) – \(t\) graph is a straight line passing through origin with slope \(2 \mathrm{~m} / \mathrm{s}^2\).
At the end of \(2 \mathrm{~s}, v=2 \times 2=4 \mathrm{~m} / \mathrm{s}\)
From \(t=2\) to \(4 \mathrm{~s}, a=0\).
Hence, \(v=4 \mathrm{~m} / \mathrm{s}\) will remain constant.
From \(t=4\) to \(6 \mathrm{~s}, a=-4 \mathrm{~m} / \mathrm{s}^2\).
Hence, \(v=u-a t=4-4 t\)
\(v=0\) at \(t=1 \mathrm{~s}\) or at \(5 \mathrm{~s}\) from origin.
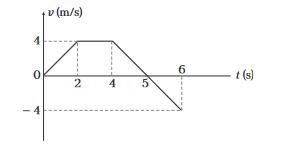
At the end of \(6 \mathrm{~s}\) (or \(t=2 \mathrm{~s}\) ) \(v=-4 \mathrm{~m} / \mathrm{s}\).
Corresponding \(v-t\) graph as shown below.

Key points regarding kinematic equations

Following are the important points in case of one dimensional motion with constant acceleration

• If the motion starts from rest, then initial velocity is taken as zero, i.e. \(u=0\).
• If the object comes to rest after the motion, then final velocity is taken as zero, i.e. \(v=0\).
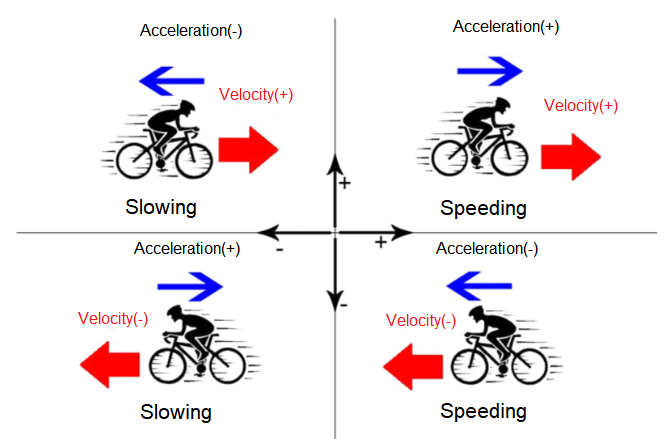
• If velocity of moving object increases with time, then acceleration is taken as positive and if velocity decreases with time, acceleration is taken as negative.
• If velocity and acceleration both have same sign like \(v>0 ; a>0\) or \(v<0 ; a<0\), then object is speeding up. Similarly, if velocity and acceleration both have opposite sign like \(v<0 ; a>0\) or \(v>0 ; a<0\). Then, the object is speeding down.
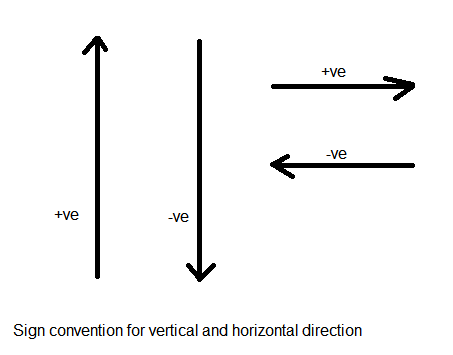
• For motion of an object along a straight line, normally we take vertically upward direction positive (and downward negative) and horizontally rightwards positive (or leftwards negative). Sign convention for (a) motion in vertical direction (b) motion in horizontal direction is shown in figure.

Example 26: Two cars start off a race with velocities \(2 \mathrm{~ms}^{-1}\) and \(4 \mathrm{~ms}^{-1}\) travel in straight line with uniform accelerations \(2 \mathrm{~ms}^{-2}\) and \(1 \mathrm{~ms}^{-2}\), respectively. What is the length of the path, if they reach the final point at the same time?

Answer: Let both cars reach at same position in same time \(t\), then
from \(\quad s=u t+\frac{1}{2} a t^2\)
For 1st car, \(s=4(t)+\frac{1}{2}(1) t^2=4 t+\frac{t^2}{2} \dots(i)\)
For 2nd car, \(s=2(t)+\frac{1}{2}(2) t^2=2 t+t^2 \dots(ii)\)
Equating above equations, we get
\(
4 t+\frac{t^2}{2}=2 t+t^2 \Rightarrow t=4 \mathrm{~s}
\)
Substituting the value of \(t\) in Eq. (i), we get
\(
s=4(4)+\frac{1}{2}(1)(4)^2=16+8=24 \mathrm{~m}
\)

Example 27: \(A\) car was moving at a rate of \(18 \mathrm{kmh}^{-1}\). When the brakes were applied, it comes to rest at a distance of \(100 \mathrm{~m}\). Calculate the retardation produced by the brakes.

Answer: Given, \(v=0, u=18 \mathrm{~kmh}^{-1}=5 \mathrm{~ms}^{-1}, s=100 \mathrm{~m}\)
Using the equation of motion,
\(
\begin{array}{rlrl}
\Rightarrow & v^2-u^2 =2 a s \dots(i) \\
\Rightarrow & -u^2 =2 a s (\because v=0) \\
\Rightarrow & a =-\frac{u^2}{2 s} \\
\Rightarrow & a =\frac{-5 \times 5}{2 \times 100}=-\frac{1}{8}=-0.125 \mathrm{~ms}^{-2}
\end{array}
\)
So, the retardation produced by the brakes is \(0.125 \mathrm{~ms}^{-2}\).

Example 28: Two car travelling towards each other on a straight road at velocity \(10 \mathrm{~ms}^{-1}\) and \(12 \mathrm{~ms}^{-1}\), respectively. When they are \(150 \mathrm{~m}\) apart, both the drivers apply their brakes and each car decelerates at \(2 \mathrm{~ms}^{-2}\) until it stops. How far apart will they be when both of them come to rest?

Answer: Let \(x_1\) and \(x_2\) be the distance travelled by the car before they stop under deceleration.
From third equation of motion,
\(
\begin{array}{rlrl}
v^2 & =u^2+2 a s \\
\Rightarrow & 0 =(10)^2-2 \times 2 x_1 \Rightarrow x_1=25 \mathrm{~m} \\
\text { and } & 0 =(12)^2-2 \times 2 x_2 \Rightarrow x_2=36 \mathrm{~m}
\end{array}
\)
Total distance covered by the two cars
\(
=x_1+x_2=25+36=61 \mathrm{~m}
\)
Distance between the two cars when they stop
\(
=150-61=89 \mathrm{~m}
\)

Example 29: A train travelling at \(20 \mathrm{kmh}^{-1}\) is approaching a platform. A bird is sitting on a pole on the platform. When the train is at a distance of \(2 \mathrm{~km}\) from pole, brakes are applied which produce a uniform deceleration in it. At that instant, the bird flies towards the train at \(60 \mathrm{kmh}^{-1}\) and after touching the nearest point on the train flies back to the pole and then flies towards the train and continues repeating itself. Calculate how much distance the bird covers before the train stops?

Answer: For retardation of train, \(v^2=u^2+2 a\) s
\(
\begin{array}{ll}
\Rightarrow & 0=(20)^2+2(a)(2) \\
\Rightarrow & a=-100 \mathrm{kmh}^{-2}
\end{array}
\)
Time required to stop the train, \(v=u+a t\)
\(
\begin{array}{l}
\Rightarrow \quad 0=20-100 t \Rightarrow t=\frac{1}{5} \mathrm{~h} \\
\text { For bird, speed }=\frac{\text { distance }}{\text { time }} \\
\Rightarrow \quad s_B=v_B \times t=60 \times \frac{1}{5}=12 \mathrm{~km}
\end{array}
\)

Example 30: In a car race, car A takes a time t less than car \(B\) at the finish point and passes the finishing point with speed \(v\) more than that of the car B. Assuming that both the cars starts from rest and travel with constant acceleration \(a_1\) and \(a_2\), respectively. Show that \(v=\sqrt{a_1 a_2} t\).

Answer: Let \(A\) takes \(t_1\) second, then according to the given problem \(B\) will take \(\left(t_1+t\right)\) seconds. Further, let \(v_1\) be the velocity of \(B\) at finishing point, then velocity of \(A\) will be \(\left(v_1+v\right)\). Writing equations of motion for \(A\) and \(B\),
\(
\begin{aligned}
v_1+v & =a_1 t_1 \dots(i) \\
v_1 & =a_2\left(t_1+t\right) \dots(ii)
\end{aligned}
\)
From these two equations, we get
\(
v=\left(a_1-a_2\right) t_1-a_2 t \dots(iii)
\)
Total distance travelled by both the cars is equal. or
\(
\begin{array}{c}
s_A=s_B \\
\frac{1}{2} a_1 t_1^2=\frac{1}{2} a_2\left(t_1+t\right)^2
\end{array}
\)
or \(t_1=\frac{\sqrt{a_2} t}{\sqrt{a_1}-\sqrt{a_2}}\)
Substituting this value of \(t_1\) in Eq. (iii), we get
\(
v=\left(\sqrt{a_1 a_2}\right) t
\)

Example 31: A particle starts with an initial velocity and passes successively over the two halves of a given distance with accelerations \(a_1\) and \(a_2\), respectively. Show that the final velocity is the same as if the whole distance is covered with a uniform acceleration \(\frac{\left(a_1+a_2\right)}{2}\).

Answer: In the first case

\(
\begin{array}{l}
v_1^2=u^2+2 a_1 s \dots(i) \\
v_2^2=v_1^2+2 a_2 s \dots(ii)
\end{array}
\)
Adding Eqs. (i) and (ii), we get
\(
v_2^2=u^2+2\left(\frac{a_1+a_2}{2}\right)(2 s) \dots(iii)
\)
In the second case,
\(
v^2=u^2+2\left(\frac{a_1+a_2}{2}\right)(2 s) \dots(iv)
\)
From Eqns. (iii) and (iv), we can see that
\(
v_2=v
\)

Example 32: A body starting from rest has an acceleration of \(4 \mathrm{~ms}^{-2}\). Calculate distance travelled by it in 5 th second.

Answer: Given, \(u=0, a=4 \mathrm{~ms}^{-2}\)
Distance travelled by the body in 5th second is
\(
\begin{aligned}
s_n & =u+\frac{1}{2} a(2 n-1) \\
s_5 & =0+\frac{1}{2} \times 4(2 \times 5-1) \\
& =\frac{1}{2} \times 4(9)=\frac{36}{2}=18 \mathrm{~m}
\end{aligned}
\)

Example 33: A particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of displacement (i) in successive second and (ii) in successive time interval \(t_0\).

Answer: (i) Displacement in \(1 \mathrm{~s}\) or \(1 \mathrm{st}\) second,
\(
\begin{aligned}
s_1 & =u t+\frac{1}{2} a t^2=0+\frac{1}{2} a(1)^2=\frac{1}{2} a \\
\text { or } \quad s_1 & =u+\frac{1}{2} a(2 t-1)=0+\frac{1}{2} a(2 \times 1-1)=\frac{1}{2} a
\end{aligned}
\)
Displacement in the 2nd second,
\(
s_2=u+\frac{1}{2} a(2 t-1)=0+\frac{1}{2} a(2 \times 2-1)=\frac{3}{2} a
\)
Displacement in the 3rd second,
\(
\begin{array}{c}
s_3=0+\frac{1}{2} a(2 \times 3-1)=\frac{5}{2} a \\
s_1: s_2: s_3: \ldots=\frac{1}{2} a: \frac{3}{2} a: \frac{5}{2} a: \ldots=1: 3: 5: \ldots
\end{array}
\)

(ii)

\(A\) to \(B\) : Displacement in the first \(t_0\) second,
\(
s=u t+\frac{1}{2} a t^2 \Rightarrow s_1=0+\frac{1}{2} a t_0^2=\frac{1}{2} a t_0^2
\)
\(A\) to \(C\):
\(
\begin{aligned}
t & =t_0+t_0=2 t_0 \\
s_1+s_2 & =0+\frac{1}{2} a\left(t_0+t_0\right)^2=2 a t_0^2
\end{aligned}
\)
Displacement in the next \(t_0\) second,
\(
s_2=\frac{3}{2} a t_0^2
\)
\(A\) to \(D\):
\(
\begin{aligned}
t & =t_0+t_0+t_0=3 t_0 \\
s_1+s_2+s_3 & =0+\frac{1}{2} a\left(t_0+t_0+t_0\right)^2=\frac{9}{2} a t_0^2
\end{aligned}
\)
Displacement in the next \(t_0\) second,
\(
s_3=\frac{5}{2} a t_0^2 \Rightarrow s_1: s_2: s_3=1: 3: 5
\)

Motion Under Gravity

The objects falling towards the earth under the influence of gravitational force alone, are called freely falling objects and such fall is called free fall. Whenever an object falls towards the earth, an acceleration is involved, this acceleration is due to the earth’s gravitational pull and is called acceleration due to gravity. The value of acceleration due to gravity near the earth surface is \(9.8 \mathrm{~ms}^{-2}\). It is independent of the mass of freely falling objects and is denoted by \(g\).
Though the value of \(g\) is independent of freely falling mass, a feather falls much slowly than a coin when released from a height. This is due to the resistance offered by air to the falling mass. If both the bodies were released at the same time in vacuum (no air resistance), they would reach the earth surface within the same duration of time.

Equations for motion under gravity

When the objects fall under the influence of gravity, its motion is uniformly accelerated motion. Hence, equations of motion are applicable in this case also. Equation for motion under gravity are given below

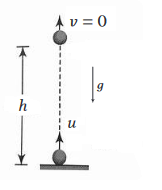
Case-1: If particle is thrown vertically upwards

In this case, applicable kinematics relations are (In this case, acceleration due to gravity is taken as negative.)

\(
\begin{aligned}
v & =u-g t \dots(i) \\
h & =u t-\frac{1}{2} g t^2 \dots(ii) \\
v^2 & =u^2-2 g h \dots(iii) 
\end{aligned}
\)

Here, \(h\) is the vertical height of the particle in upward direction.
In this case, acceleration due to gravity is taken as negative.
At maximum height (say \(h\) ), \(v=0\)
\((\because\) at maximum height, the particle stops moving upwards that means its velocity becomes zero)
\(\therefore\) From the Eq. (i), \(u=g t\)
or \(t=\frac{u}{g}\), which is called time of ascent.
For motion under gravity, for the same distance, the time taken to go up is same as time taken to fall down.
\(\therefore\) Time of ascent \(=\) Time of descent
Total flight time, \(T=2 \times\) Time of ascent or descent
Total flight time \((T)=\frac{2 u}{g}\)
From Eqns. (ii) and (iii), we get
\(
h=\frac{1}{2} g t^2
\)
and
\(
u^2=2 g h \text { or } h=\frac{u^2}{2 g}
\)

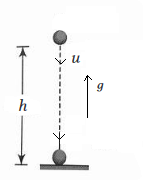
Case-2: If particle is thrown vertically downward with some velocity from some height.

In this case,
\(
\begin{array}{l}
v=u+g t \\
h=u t+\frac{1}{2} g t^2 \\
v^2=u^2+2 g h
\end{array}
\)
Here, \(h\) is the vertical height of particle in downward direction. In this case, acceleration due to gravity is taken as positive.

Case-3: If a particle is dropped from some height.

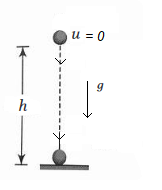
In this case, initial velocity is taken zero \((u=0)\), so equations of motion are
\(
\begin{aligned}
v & =g t \dots(i) \\
h & =\frac{1}{2} g t^2 \dots(ii) \\
v^2 & =2 g h \dots(iii)
\end{aligned}
\)
For fast calculation in objective problems, remember the following results
(a) Maximum height attained by a particle, thrown upwards from ground,
\(
h=\frac{u^2}{2 g}
\)
(b) Velocity of particle at the time of striking the ground when released \((u=0)\) from a height \(h\) is
\(
v=\sqrt{2 g h}
\)
(c) In above point (b), time of collision of particle with ground,
\(
t=\sqrt{\frac{2 h}{g}}
\)

Example 34: A ball is thrown upwards from the top of a tower \(40 \mathrm{~m}\) high with a velocity of \(10 \mathrm{~m} / \mathrm{s}\). Find the time when it strikes the ground. (Take, \(g=10 \mathrm{~m} / \mathrm{s}^2\) )

Answer: According to the question, the condition is as shown below.

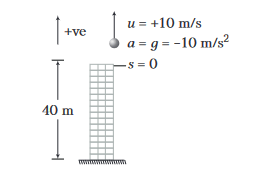
Given, \(u=+10 \mathrm{~m} / \mathrm{s}, \quad a=-10 \mathrm{~m} / \mathrm{s}^2\) and \(s=-40 \mathrm{~m}\) (at the point, where stone strikes the ground)
Substituting in \(s=u t+\frac{1}{2} a t^2\), we get
\(
-40=10 t-5 t^2 \text { or } 5 t^2-10 t-40=0
\)
or \(\quad t^2-2 t-8=0\)
Solving this, we have
\(t=4 \mathrm{~s}\) and \(-2 \mathrm{~s}\). Taking the positive value \(t=4 \mathrm{~s}\).

Example 35: A rocket is fired vertically up from the ground with a resultant vertical acceleration of \(10 \mathrm{~ms}^{-2}\). The fuel is finished in 1 min and it contiues to move up.
(i) What is the maximum height reached?
(ii) After finishing fuel, calculate the time for which it continues its upwards motion. (Take, \(g=10 \mathrm{~ms}^{-2}\) )

Answer: (i) The distance travelled by the rocket during burning of fuel \((1\) minute \(=60 \mathrm{~s})\) in which resultant acceleration is vertically upwards and is \(10 \mathrm{~ms}^{-2}\) will be \(h_1=u t+\frac{1}{2} g t^2\) \(=0 \times 60+(1 / 2) \times 10 \times 60^2=18000 \mathrm{~m}=18 \mathrm{~km}\) and velocity acquired by it will be \(v=u+a t=0+10 \times 60=600 \mathrm{~ms}^{-1}\)
Now, after \(1 \mathrm{~min}\), the rocket moves vertically up with initial velocity of \(600 \mathrm{~ms}^{-1}\) and acceleration due to gravity opposes its motion.
So, it will go to a height \(h_2\) from this point, till its velocity becomes zero such that
\(
v^2-u^2=-2 g h \Rightarrow 0-(600)^2=-2 g h_2\left(g=10 \mathrm{~ms}^{-2}\right)
\)
or \(h_2=18000 \mathrm{~m}=18 \mathrm{~km}\)
So, the maximum height reached by the rocket from the ground, \(H=h_1+h_2=18+18=36 \mathrm{~km}\)
(ii) As after burning of fuel, the initial velocity attained will be \(600 \mathrm{~ms}^{-1}\) and gravity opposes the motion of rocket, so from first equation of motion time taken by it till its velocity \(v=0\) is given as,
\(
0=600-g t \Rightarrow t=60 \mathrm{~s}
\)

Example 36: A juggler throws balls into air. He throws one ball whenever the previous one is at its highest point. How high does the balls rise, if he throws \(n\) balls each second? Acceleration due to gravity is \(g\).

Answer: Juggler throws \(n\) balls in one second, so time interval between two consecutive throws is \(t=\frac{1}{n} \mathrm{~s}\)

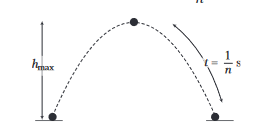
Each ball takes \(\frac{1}{n} \mathrm{~s}\) to reach maximum height.
So, \(\quad h_{\max }=\frac{1}{2} \times g t^2=\frac{1}{2} \times g\left(\frac{1}{n}\right)^2 \Rightarrow h_{\max }=\frac{g}{2 n^2}\)

Example 37: From an elevated point \(A\), a stone is projected vertically upwards. When the stone reaches a distance \(h\) below \(A\), its velocity is double of what it was at a height \(h\) above \(A\). Show that the greatest height attained by the stone is \(\frac{5}{3} h\).

Answer: Let \(u\) be the velocity with which the stone is projected vertically upwards.
Given, \(\quad v_{-h}=2 v_h\) or \(\left(v_{-h}\right)^2=4 v_h^2\)
According to the kinematic equation,
\(
v_h^2=u^2-2 g h
\)
and
\(
v_{-h}^2=u^2-2 g(-h)
\)
\(
\begin{aligned}
& \Rightarrow & u^2-2 g(-h) & =4\left(u^2-2 g h\right) \\
& \therefore & u^2 & =\frac{10 g h}{3}
\end{aligned}
\)
Now, maximum height, \(h_{\max }=\frac{u^2}{2 g}=\frac{5 h}{3}\)

Example 38: \(A\) ball is thrown vertically upwards with a velocity of \(20 \mathrm{~ms}^{-1}\) from the top of a multistorey building. The height of the point from where the ball is thrown is \(25 \mathrm{~m}\) from the ground. How long it will take before the ball hits the ground? (Take, \(g=10 \mathrm{~ms}^{-2}\) )

Answer: Let us take the positive \(Y\)-axis in the vertically upward direction with zero at the ground.
Now, \(v_0=+20 \mathrm{~ms}^{-1}, a=-g=-10 \mathrm{~ms}^{-2}, v=0 \mathrm{~ms}^{-1}\)
The total time taken can also be calculated by noting the coordinates of initial and final positions of the ball with respect to the origin chosen and using equation
\(
y=y_0+v_0 t+\frac{1}{2} a t^2
\)
Now, \(y_0=25 \mathrm{~m}, y=0 \mathrm{~m}\),
\(
\begin{array}{rlrl}
v_0 & =20 \mathrm{~ms}^{-1}, a=-10 \mathrm{~ms}^{-2} \\
& \therefore & 0 & =25+20 t+\left(\frac{1}{2}\right)(-10) t^2 \\
\Rightarrow & 5 t^2-20 t-25 & =0
\end{array}
\)
Solving this quadratic equation for \(t\), we get
\(
t=5 \mathrm{~s}
\)

Example 39: A ball is thrown upwards from the ground with an initial speed \(u\). The ball is at a height of \(80 \mathrm{~m}\) at two times, for the time interval of \(6 s\). Find the value of \(u\).

Answer:

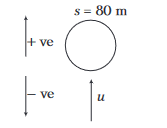
Here, \(a=g=-10 \mathrm{~ms}^{-2}\) and \(s=80 \mathrm{~m}\) Substituting the values in \(s=u t+\frac{1}{2} a t^2\), we get \(80=u t-5 t^2\)
or,  \(5 t^2-u t+80=0\)
and
\(
\begin{array}{r}
t=\frac{u+\sqrt{u^2-1600}}{10} \\
t=\frac{u-\sqrt{u^2-1600}}{10}
\end{array}
\)
Now, it is given that
\(
\frac{u+\sqrt{u^2-1600}}{10}-\frac{u-\sqrt{u^2-1600}}{10}=6
\)
\(
\begin{array}{l}
\Rightarrow \quad \frac{\sqrt{u^2-1600}}{5}=6 \\
\Rightarrow \sqrt{u^2-1600}=30 \\
\Rightarrow \quad u^2-1600=900 \\
\therefore \quad u^2=2500 \\
\Rightarrow \quad u= \pm 50 \mathrm{~ms}^{-1} \\
\end{array}
\)
Ignoring the negative sign, we get
\(
u=50 \mathrm{~ms}^{-1}
\)

Example 40: A particle is thrown vertically upwards from the surface of the earth. Let \(T_P\) be the time taken by the particle to travel from a point \(P\) above the earth to its highest point and back to the point \(P\).
Similarly, let \(T_Q\) be the time taken by the particle to travel from another point \(Q\) above the earth to its highest point and back to the same point \(Q\). If the distance between the points \(P\) and \(Q\) is \(H\), find the expression for acceleration due to gravity in terms of \(T_P, T_Q\) and \(H\).

Answer:

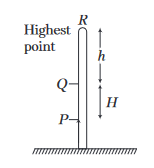
Time taken by the particle to travel from point \(P\) back to point \(P\),
\(
T_P=T_{P R}+T_{R P}
\)
Here, \(T_{P R}=T_{R P}\), then \(T_P=2 T_{P R}\)
Using second equation of motion,
\(
(H+h)=\frac{1}{2} g T_{P R}^2
\)
\(
\begin{array}{l}
\Rightarrow \quad T_{P R}=\sqrt{2 \frac{(H+h)}{g}} \\
\Rightarrow \quad T_P=2 \sqrt{\frac{2(H+h)}{g}}
\end{array}
\)
Then, similarly time taken by the particle to travel from point \(Q\) back to point \(Q\),
\(
\begin{aligned}
T_Q & =2 \sqrt{\frac{2 h}{g}} \\
T_P^2 & =\frac{8(h+H)}{g} \\
\text { and } \quad T_Q^2 & =\frac{8 h}{g} \\
\Rightarrow \quad T_P^2 & =T_Q^2+\frac{8 H}{g} \Rightarrow g=\frac{8 H}{T_P^2-T_Q^2}
\end{aligned}
\)

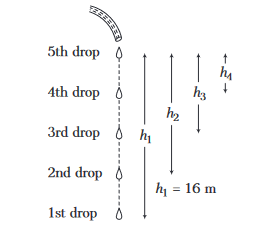
Example 41: From the top of a building, \(16 \mathrm{~m}\) high water drops are falling at equal intervals of time such that when the first drop reaches the ground, the fifth drop just starts. Find the distance between the successive drops at that instant.

Answer: Let the interval of time be \(t_0\).
First drop is released at \(t=0\), second drop at \(t=t_0\), third drop at \(t=2 t_0\), fourth drop at \(t=3 t_0\), fifth drop at \(t=4 t_0\).
Therefore, first drop has fallen for time \(4 t_0\), second drop for \(3 t_0\), third drop for \(2 t_0\), fourth drop for \(t_0\) when fifth drop is about to fall. The location of drops are as shown in the figure.

For 1st drop,
\(
\begin{aligned}
h_1 & =\frac{1}{2} g\left(4 t_0\right)^2, \quad 16=\frac{1}{2} g \times 16 t_0^2 \\
\frac{1}{2} g t_0^2 & =1 \mathrm{~m}
\end{aligned}
\)
For 2nd drop, \(h_2=\frac{1}{2} g\left(3 t_0\right)^2=9 \mathrm{~m}\)
For 3rd drop, \(h_3=\frac{1}{2} g\left(2 t_0\right)^2=4 \mathrm{~m}\)
For 4th drop, \(h_4=\frac{1}{2} g t_0^2=1 \mathrm{~m}\)
For 5th drop, \(h_5=0\)
Separation between drops
1st and \(2 \mathrm{nd}: h_1-h_2=7 \mathrm{~m}\)
2nd and 3rd : \(h_2-h_3=5 \mathrm{~m}\)
3rd and 4th : \(h_3-h_4=3 \mathrm{~m}\)
4th and 5th : \(h_4-h_5=1 \mathrm{~m}\)
Note: If the 1st drop is at the ground and the 5th drop is about to fall, the time for which the first drop has fallen \((5-1) t_0=4 t_0\) where \(t_0\) is the regular interval of time.

Example 42: A ball is dropped from the top of a tower. After \(2 s\) another ball is thrown vertically downwards with a speed of \(40 \mathrm{~ms}^{-1}\). After how much time and at what distance below the top of tower the balls meet?

Answer: Let the balls meet at distance \(h\) below the top of tower at \(t\) second after dropping of first ball. The second ball takes time \((t-2)\) seconds.

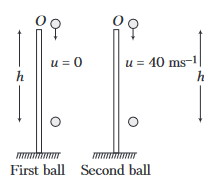
For first ball, \(h=\frac{1}{2} g t^2 \dots(i)\)
For second ball, \(h=40(t-2)+\frac{1}{2} g(t-2)^2 \dots(ii)\)
From Eqs. (i) and (ii), we get
\(
\begin{array}{c}
40(t-2)+\frac{1}{2} g(t-2)^2=\frac{1}{2} g t^2 \\
40(t-2)=\frac{1}{2} g\left[t^2-(t-2)^2\right] \\
40(t-2)=\frac{1}{2} \times 10(2 t-2) \times 2 \\
4 t-8=2 t-2 \Rightarrow t=3 \mathrm{~s}
\end{array}
\)
Distance below the top of tower, where the balls meet,
\(
h=\frac{1}{2} g t^2=\frac{1}{2} \times 10 \times 3^2=45 \mathrm{~m}
\)

Non-Uniformly Accelerated Motion

When acceleration of particle is not constant, motion is known as non-uniformly accelerated motion. For example, Consider a body moving along a straight line, and let the velocity at a point \(\mathrm{O}\) be \(10 \frac{\mathrm{m}}{\mathrm{s}}\), when the stop watch is started, the velocity of the body is found to be \(12 \frac{\mathrm{m}}{\mathrm{s}}, 15 \frac{\mathrm{m}}{\mathrm{s}}, 19 \frac{\mathrm{m}}{\mathrm{s}}\) and \(26 \frac{\mathrm{m}}{\mathrm{s}}\), while at A,B,C, and D at time \(1,2,3\) and 4 seconds respectively. It is clear that in each interval of \(1 \mathrm{~s}\) the velocity changes by different. Such a body is said to be in non-uniform acceleration .

Then, basic equations of velocity and acceleration can be written as

• \(\mathbf{v}=\frac{d \mathbf{s}}{d t}\) or sometimes \(\mathbf{v}=\frac{d \mathbf{r}}{d t}\)
• \(\mathbf{a}=\frac{d \mathbf{v}}{d t}\)
• \(d \mathbf{s}=\mathbf{v} d t\)
• \(d \mathbf{v}=\mathbf{a} d t\)

For one dimensional motion, above relations can be written as under

• \(v=\frac{d s}{d t}\)
• \(a=\frac{d v}{d t}=v \frac{d v}{d s}\)
• \(d s=v d t\) and
• \(d v=a d t \quad\) or \(\quad v d v=a d s\)

Such problems can be solved either by differentiation or integration (with some boundary conditions).
\(
s-t \longrightarrow v-t \longrightarrow a-t \quad \text { (Differentiation) }
\)
\(
a-t \longrightarrow v-t \longrightarrow s-t \quad \text { (Integration with boundary conditions) }
\)

Note: 

• By boundary condition, we mean that velocity or displacement at some time (usually at \(t=0\) ) should be known to us. Otherwise we cannot find constant of integration.
• Equation \(\mathbf{a}=\mathbf{v} d \mathbf{v} / d \mathbf{s}\) or \(\mathbf{v} d \mathbf{v}=\mathbf{a} d \mathbf{s}\) is useful when acceleration-displacement equation is known and velocity-displacement equation is required.

Example 43: Velocity-time equation of a particle moving in a straight line is
\(
v=\left(10+2 t+3 t^2\right) \text { (SI units) }
\)
Find
(i) displacement of particle from the mean position at time \(t=1 \mathrm{~s}\), if it is given that displacement is \(20 \mathrm{~m}\) at time \(t=0\).
(ii) and acceleration-time equation.

Answer: (i) The given equation can be written as
\(
v=\frac{d s}{d t}=\left(10+2 t+3 t^2\right) \dots(i)
\)
\(
\begin{aligned}
d s & =\left(10+2 t+3 t^2\right) d t \\
\int_{20}^s d s & =\int_0^1\left(10+2 t+3 t^2\right) d t \\
s-20 & =\left[10 t+t^2+t^3\right]_0^1 \\
s & =20+12=32 \mathrm{~m}
\end{aligned}
\)
(ii) Acceleration-time equation can be obtained by differentiating Eq. (i) w.r.t. time. Thus,
\(
\begin{array}{l}
a=\frac{d v}{d t}=\frac{d}{d t}\left(10+2 t+3 t^2\right) \\
a=2+6 t
\end{array}
\)

Example 44: Displacement-time equation of a particle moving along \(X\)-axis is
\(
x=20+t^3-12 t \text { (SI units) }
\)
(i) Find position and velocity of particle at time \(t=0\).
(ii) State whether the motion is uniformly accelerated or not.
(iii) Find position of particle when velocity of particle is zero.

Answer: (i) Given, displacement-time equation of a particle
\(
x=20+t^3-12 t \dots(i)
\)
At \(t=0 \quad x=20+0-0=20 \mathrm{~m}\)
Velocity of particle at time \(t\) can be obtained by differentiating Eq. (i) w.r.t. time, ie.
\(
v=\frac{d x}{d t}=3 t^2-12 \dots(ii)
\)
At \(t=0, v=0-12=-12 \mathrm{~m} / \mathrm{s}\)
(ii) Differentiating Eq. (ii) w.r.t. time \(t\), we get the acceleration,
\(
a=\frac{d v}{d t}=6 t
\)
As acceleration is a function of time, the motion is non-uniformly accelerated motion.
(iii) Substituting \(v=0\) in Eq. (ii), we get
\(
0=3 t^2-12
\)
Positive value of \(t\) comes out to be \(2 \mathrm{~s}\) from this equation. Substituting \(t=2 \mathrm{~s}\) in Eq. (i), we get
\(
x=20+(2)^3-12(2) \text { or } x=4 \mathrm{~m}
\)

Example 45: The velocity of particle moving in the positive direction of \(X\)-axis varies as \(v=\alpha \sqrt{x}\), where \(\alpha\) is a positive constant. Assuming that at moment \(t=0\), the particle was located at the point \(x=0\).
Find
(i) the time dependence of the velocity of the particle.
(ii) the mean velocity of the particle averaged over the time that the particle takes to cover first s metres of the path.

Answer: (i) Given, the velocity of the particle moving in the positive direction of \(X\)-axis,
\(
\begin{array}{rlrl}
v & =\alpha \sqrt{x} \\
\Rightarrow \quad & \frac{d x}{d t} & =\alpha \sqrt{x}
\end{array}
\)
By integrating \(\int_0^x \frac{d x}{\sqrt{x}}=\alpha \int_0^t d t\)
\(
\begin{aligned}
\Rightarrow & \frac{x^{-1 / 2+1}}{-(1 / 2)+1} & =\alpha t \\
\Rightarrow & x =\frac{\alpha^2 t^2}{4}
\end{aligned}
\)
(ii) Distance, \(x=\frac{\alpha^2 t^2}{4}\); for \(s\) distance \(s=\frac{\alpha^2 t^2}{4}\)
Time taken to cover first \(s\) distance, \(t=\sqrt{\frac{4 s}{\alpha^2}}\) The mean velocity of the particle,
\(
v_{\mathrm{av}}=\frac{s}{t}=\frac{s}{\sqrt{4 s / \alpha^2}}=\frac{\alpha \sqrt{s}}{2}
\)