Geometric Probability

Geometric probability describes the chance that a point lies on a part of a line segment or on a part of a region. When a problem appears to have countless possible outcomes, graphing can be a useful tool for solving probability problems. When calculating geometric probabilities, it is useful to have a general knowledge of some basic area formulas.

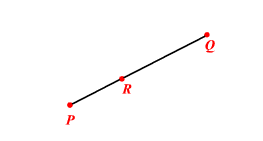
Example 1: \(\text { Consider the line segment } \overline{P Q} \text { Suppose a point } X \text { is picked at random. }\) Find the \(\text { probability of } X \text { is on } \overline{P R}\)

Solution:

\(
\text { The probability of } X \text { is on } \overline{P R}=\frac{\text { Length of } \overline{P R}}{\text { Length of } \overline{P Q}} \text {. }
\)

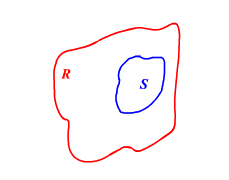
Example 2: \(\text { Consider the region }{R} \text { and the region } S \text {. Suppose a point } P \text { is picked at random. }\)\(\text { Find the probability of } P \text { is in } S\)

Solution:

\(
\text { The probability of } P \text { is in } S=\frac{\text { Area of } S}{\text { Area of } R} \text {. }
\)

Example 3: \(\text { Find the probability that a point chosen at random lies on } \overline{A C} \text {. }\)

Solution:

Probability of the point is on \(\overline{A C}=\frac{\text { Length of } A C}{\text { Length of } A B}\)
Use the Segment Addition Postulate to find the length of \(\overline{A B}\)
\(
\begin{aligned}
& A B=A C+C B \\
& =3+9 \\
& =12
\end{aligned}
\)
Probability of the point is on \(\overline{A C}=\frac{3}{12}\)
\(
=\frac{1}{4}
\)
The probability of the point is on \(\overline{A C}\) is \(=\frac{1}{4}\) or \(0.25\).

Example 4: A dart is thrown at random onto a board that has the shape of a circle as shown below. Calculate the probability that the dart will hit the shaded region. (Use \(\pi=3.142\) )

Solution:

Total area of board \(=3.142 \times 14^2=615.83 \mathrm{~cm}^2\)
Area of non-shaded circle \(=3.142 \times 7^2=153.99 \mathrm{~cm}^2\)
Area of shaded region \(=615.83-153.99=461.84 \mathrm{~cm}^2=462 \mathrm{~cm}^2\) (rounded to whole number)
Probability of hitting the shaded region \(=\frac{462}{616}=\frac{3}{4}\)

Example 5: The figure shows a circle divided into sectors of different colors. 

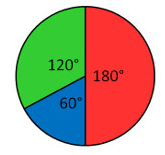
If a point is selected at random in the circle, calculate the probability that it lies:
(a) in the red sector
(b) in the green sector.
(c) in any sector except the green sector.

Solution:

Total area of board \(=3.142 \times 14^2=615.83 \mathrm{~cm}^2\)
(a) Area of red sector \(=\frac{1}{2} \times\) area of circle
Probability that the point lies on red sector \(=\frac{1}{2}\)
(b) Area of green sector \(=\frac{1}{3} \times\) area of circle
Probability that the point lies on green sector \(=\frac{1}{3}\)
(c) In any sector except the green sector.
The probability that the point does not lie in the green sector \(=1-\frac{1}{3}=\frac{2}{3}\)

Example 6: In the figure below, PQRS is a rectangle, and A, B, C, and D are the midpoints of the respective sides as shown.

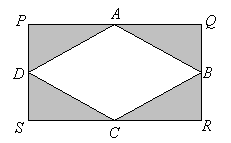
An arrow is shot at random onto the rectangle PQRS. Calculate the probability that the arrow strikes:
(a) triangle AQB.
(b) a shaded region.
(c) either triangle BRC or the unshaded region.

Solution:

(a) Let \(P Q=2 x\) and \(Q R=2 y\). Then, \(A Q=x\) and \(Q B=y\).
Area of rectangle PQRS \(=2 x \times 2 y=4 x y\)
Area \(\mathrm{AQB}=\frac{1}{2} \mathrm{xy}\)
Probability of striking triangle \(A Q B=\frac{1}{2} x y \div 4 x y=\frac{1}{8}\)

(b) All the shaded triangles are equal.
Total area of shaded regions \(=4 \times \frac{1}{2} x y=2 x y\)
Probability of striking a shaded region \(=2 x y \div 4 x y=\frac{1}{2}\)

(c) Area of unshaded region \(=4 x y-2 x y=2 x y\)
Probability of striking unshaded region \(=2 x y \div 4 x y=\frac{1}{2}\)
Area of triangle \(B R C=\frac{1}{2} x y\)
Probability of striking triangle \(B R C=\frac{1}{2} x y \div 4 x y=\frac{1}{8}\)
Probability of striking triangle BRC or unshaded region \(=\frac{1}{2}+\frac{1}{8}=\frac{5}{8}\)

Example 7: A target shown in the given figure consists of three concentric circles of radii 3, 7, and 9 cm respectively. A dart is thrown and lands on the target. What is the probability that the dart will land on the shaded region?

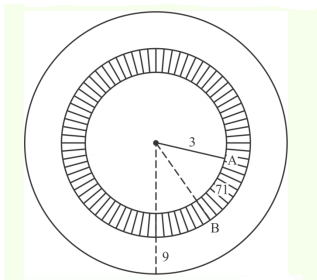
Solution:

Given: A target is shown in figure consists of three concentric circles of radius 3, 7, and 9 cm. A dart is thrown and lands on the target.
To find: Probability that the dart will land in the shaded region?
The total area of the circle with a radius of 9 cm.
\(
\begin{aligned}
& \text { Area of circle with radius }
9 \mathrm{~cm}  =\pi r^2 \\
& =\pi(9)^2 \\
& =81 \pi \mathrm{cm}^2 \\
& \text { Area of shaded portion }  =\pi\left(R^2-r^2\right) \\
& =\pi\left(7^2-3^2\right) \\
& =\pi(7+3)(7-3) \\
& =\pi(10)(4) \\
& =40 \pi
\end{aligned}
\)
We know that Probability \(=\frac{\text { Number of favourable event }}{\text { Total number of event }}\)
Hence the probability of the spinner will land in the shaded region is \(\frac{40 \pi}{81 \pi}=\frac{40}{81}\)

Example 8: A dart board is a regular octagon divided into regions as shown. Suppose that a dart thrown at the board is equally likely to land anywhere on the board. What is the probability that the dart lands within the center square?

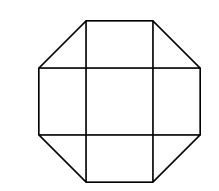
Solution:

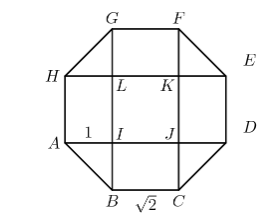
If the side lengths of the dartboard and the side lengths of the center square are all \(\sqrt{2}\), then the side length of the legs of the triangles are 1.
\(
\begin{aligned}
\text { area of center square }: & \sqrt{2} \times \sqrt{2}=2 \\
\text { total area } & (\sqrt{2})^2+4(1 \times \sqrt{2})+4\left(1 \times 1 \times \frac{1}{2}\right)=2+4 \sqrt{2}+2=4+4 \sqrt{2}
\end{aligned}
\)
Use Geometric probability by putting the area of the desired region over the area of the entire region.
\(
\frac{2}{4+4 \sqrt{2}}=\frac{1}{2+2 \sqrt{2}} \times \frac{2-2 \sqrt{2}}{2-2 \sqrt{2}}=\frac{2-2 \sqrt{2}}{-4}=\frac{\sqrt{2}-1}{2}
\)

Example 9: Find the geometric probability of selecting a girl from a class, if the girls of the class are represented by a circle of radius 3.5 cms, and the entire class of students is represented by a larger square of side 8 cms.

Solution:

Given that the girls represent the circle if radius \(3.5 \mathrm{cms}\), and the entire class of students represent a square of side \(8 \mathrm{cms}\).
Area of the circle \(=\pi r^2=22 / 7 \times 3.5 \times 3.5=38.5\)
Area of the square \(=s^2=8 \times 8=64\)
Probability of selecting the girl = Area of Circle/Area of Square
Probability of selecting the girl \(=38.5 / 64\)
Therefore the probability of selecting the girl from the class of students is \(38.5 / 64\).

Example 10: Find the geometric probability of the number of students who can speak English, if the people are represented s sectors in a circle, and the English-speaking people represent a sector of \(120^{\circ}\)

Solution:

The number of people who speak English is represented by a sector of angle \(120^{\circ}\), and the total number of students in the class are represented by the entire circle, which is an angle of \(360^{\circ}\).
Probability of people speaking English = Area of sector/Area of circle \(=\) Angle of the sector/Complete angle
Probability of people speaking English \(=120^{\circ} / 360^{\circ}=1 / 3\)
Therefore the probability of people speaking the English language is \(1 / 3\).

Example 11: ABCD is a square. M is the midpoint of BC and N is the midpoint of CD. A point is selected at random in the square. Calculate the probability that it lies in the triangle MCN.

Solution:

Let \(2 x\) be the length of the square.
Area of square \(=2 x \times 2 x=4 x^2\)
Area of triangle \(M C N=\frac{1}{2} x^2\)
\(
\begin{aligned}
\mathrm{P}(\text { point in the triangle }) & =\frac{1}{2} x^2 \div 4 x^2 \\
& =\frac{1}{2} x^2 \times \frac{1}{4 x^2} \\
& =\frac{1}{8}
\end{aligned}
\)

Example 12: The figure shows a circle with center O and a radius 8 cm. The radius of the smaller circle is 4 cm. A point is selected at random inside the larger circle BCDE. Angle BOD = \(72^{\circ}\)

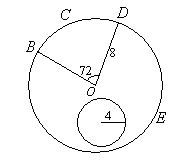
Calculate the probability that the point lies
(a) inside the sector BODC.
(b) inside the smaller circle
(c) neither in the sector BODC nor in the smaller circle.

Solution:

(a) \(\frac{72}{360}=\frac{1}{5}\)
Area of sector \(B O D C=\frac{1}{5} \times\) area of the large circle
The probability that the point lies in the sector \(B O D C=\frac{1}{5}\)
(b) \(\frac{\text { area of smaller circle }}{\text { area of larger circle }}=\frac{\pi \times 4^2}{\pi \times 8^2}=\frac{1}{4}\)
Area of smaller circle \(=\frac{1}{4} \times\) area of the large circle
The probability that the point lies in the smaller circle \(=\frac{1}{4}\)
(c) Probability that the point does not lie in the sector \(B O D C\) or the smaller circle = \(P(t w \circ\) black balls \()=\frac{3}{8} \times \frac{3}{8}=\frac{9}{64}\)